网络条件下轨道交通开行方案协调优化研究
孙梦霞,倪少权,吕红霞
网络条件下轨道交通开行方案协调优化研究
孙梦霞,倪少权,吕红霞
(1. 西南交通大学,交通运输与物流学院 成都 611756;2. 西南交通大学,全国铁路列车运行图编制研发培训中心 成都 611756;3. 综合交通运输智能化国家地方联合工程实验室 成都 611756)
在轨道交通网络化运营条件下, 考虑不同线路间乘客的脉冲性到达特征和拥挤度对乘客出行行为选择的影响, 对轨道交通网络列车开行方案进行协调优化。以轨道交通运营企业成本和广义乘客出行费用之和最小为目标, 构建列车开行方案优化模型, 对路网中各条线路的列车发车间隔和各线路间的发车时刻相位差进行优化, 并结合客流的离散性特征和模型结构, 提出了一种基于仿真的遗传算法对该模型进行求解。给定某轨道交通网络, 实例验证了所提出模型和算法的有效性。计算结果表明, 相较于现有优化方法, 本文所提出的优化模型能够有效降低网络化运营条件下的系统总成本, 在提高轨道交通运营企业效益的同时降低了乘客的广义出行费用。
城市轨道交通;列车开行方案;遗传算法;发车间隔;网络化运营
0 引 言
近年来,随着轨道交通建设的推进,主要城市轨道交通已步入网络化运营时代。相较于单条线路的运输组织,网络化运营条件下,存在大量换乘乘客,客流需求多样化,对各线路协同运行提出了更高的要求。因此,如何考虑路网客流需求,制定合理高效的列车开行方案具有重要意义。
针对此类问题,国内外学者进行了诸多研究。禹丹丹等[1]从加强换乘站的换乘接续出发,采用混合整数规划方法对轨道交通网列车时刻表进行优化,并通过平均换乘等待时间缩小变量规模;Liebchen[2]以最小化乘客换乘等待时间为目标,研究了城市轨道交通列车开行方案优化问题;汪波等[3]分析了制约轨道交通运力配置的影响因素,针对不同运营模式下的轨道交通网,对运力配置问题进行了优化;汪波等[4]引入了周期事件安排问题来描述列车开行方案优化,建立了城市轨道交通网络运行图编制模型,并采用选择合适约束图生成树的方法简化模型;王永亮等[5]以乘客成本和运营企业成本之和最小为目标,建立了列车开行方案的双层规划模型并求解。上述研究在一定程度上对列车开行方案进行了优化,但在换乘协调方面,未考虑换乘人数对换乘效果的影响以及换乘客流到达的脉冲性特征。殷瑞琴等[6]优先考虑乘客需求,采用改进的Edmond算法对轨道交通末班车时刻表进行了优化;Ting等[7]通过发车间隔和缓冲时间刻画列车在区间运行时分的不稳定性,设计启发式算法对具有多个换乘站的轨道交通网络列车开行方案进行了协调优化;Ibarra-Rojas等[8]综合考虑乘客换乘效率最大化和公交客流组团到达概率最小化,证明了该问题的NP-hard属性,根据模型结构设计启发式算法对墨西哥城的公交网络开行方案进行了协调优化;Wong等[9]以换乘乘客的换乘等待总时间最小为目标,以城市轨道交通列车出发时间、到达时间、停站时间和区间运行时分为决策变量,针对轨道交通网列车开行方案优化问题建立了模型,以香港地铁为例验证了模型和算法的有效性;Shafahi等[10]针对轨道交通网络,描述了每个乘客的平均换乘等待时间,以固定流程的周期性事件进行建模并给出了计算方法,在此基础上,研究了城市轨道交通网络列车开行方案优化问题;Tuzunaksu等[11]对单个乘客完成一次出行的平均换乘等待时间进行了计算,针对城市轨道交通网络列车开行方案优化问题建立了模型。上述研究对轨道交通网中的列车开行方案进行了一定程度的优化,但尚未考虑大客流情况下拥挤度对乘客出行行为选择的影响。本文在现有研究的基础上,针对网络化运营的城市轨道交通系统,考虑换乘乘客的脉冲性到达特征和拥挤度对乘客出行行为选择的影响,建立了轨道交通网列车开行方案模型并求解。
1 问题说明
假设某轨道交通网为非连通型,网络内所有线路均采取相同的行车间隔时间。在各条线路上,列车从每条线路的始发车站出发,到达折返站后在折返站折返,然后返回始发车站,并在始发车站等待执行下一个交路。
为方便描述,按列车运行方向对每条线路进行拓展,构建如图1所示的拓扑网络图表示轨道交通网络。其中,以线路为单位标识各个车站,将每条线路上的各个车站由始发站按列车运行方向依次标记为车站1, 2, …

网络化运营条件下,列车开行方案制定的关键问题是根据客流情况,确定各线路发车间隔及不同线路间的发车时刻相位差。在确定路网中不同线路列车开行方案时,应充分考虑换乘需求,协调不同线路间乘客换乘需要,从轨道交通运营企业经济效益和乘客出行服务质量角度,构建模型对运营企业成本和乘客出行费用进行优化。为进一步方便建模,提出如下假设:①轨道交通网中乘客OD已知;②乘客在各站的到达规律服从均匀分布;③乘客具备的时间价值相同,乘客具备的拥挤敏感度相同;④乘客通过轨道交通出行时,会优先选择换乘次数最少的径路,若多条径路换乘次数相同,以出行时间为序,优先选择出行时间最短的径路出行;⑤对于同一换乘站的同一换乘方向,换乘乘客在换乘时消耗的走行时间相同;⑥出发乘客在站台等待时,会乘坐与其出行方向一致且最先到达的出发列车,换乘乘客在站台等待时,会乘坐与其出行方向一致且最先到达的换乘接续列车。
上述假设不影响模型的适用性,并能在一定程度上简化建模及求解过程。
2 模型建立
2.1 符号说明
模型参数如下:
模型变量如下:
2.2 目标函数
模型从系统角度出发,将包含轨道交通运营企业成本和乘客广义出行费用的整个系统总成本作为优化目标。其中,乘客广义出行费用又包括乘客出行时间费用和乘客出行费用。



乘客出行时间费用指乘客感知到的出行过程中由于时间的消耗而使乘客感受到的成本。为方便描述,利用时间价值系数将乘客出行时间费用转化为广义时间成本进行计算。广义时间成本主要包括乘客初始等待时间成本、乘客乘车时间成本和乘客换乘时间成本。
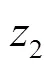

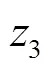
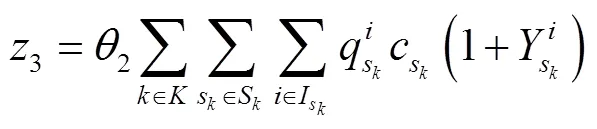
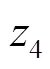
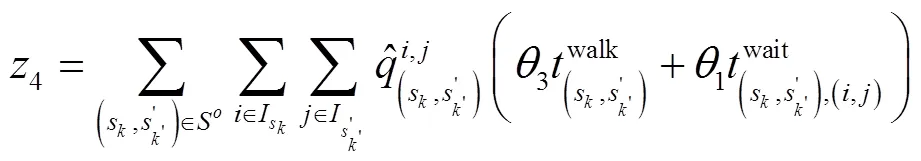
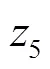

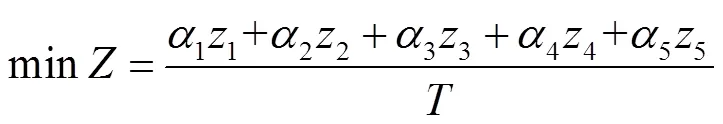
2.3 约束条件
在轨道交通网络化运营条件下,列车开行方案的制定需要满足轨道交通网中各线路的能力约束和行车间隔时间约束,并充分利用各条线路能力,满足轨道交通客流的运送需求,同时尽可能减少支出,提高乘客服务质量。城市轨道交通需要满足一定的经济效益要求[15],通常情况下,网络中各线路的效益之和不应低于一定限值,以避免长期亏损运营。
(1)列车容量约束:
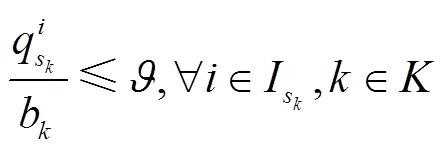
(2)各线路发车间隔约束:
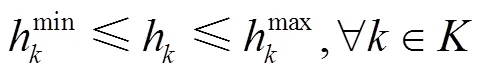
(3)各线路与线路1在始发站的发车时刻相位差约束:
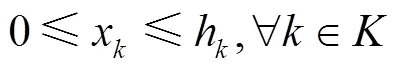
(4)站台容量约束:

(5)收益约束:

2.4 求解方法
轨道交通网络中,系统中的客流变化过程呈一定的离散性,难以通过数学公式给出精确描述。本文结合所建模型的结构特征,提出一种基于仿真的遗传算法对该模型进行求解,求解步骤如下:
step1 设定优化精度。为保证模型的可求解性,首先给定一个优化精度,确保给定的优化精度能被所有事件的持续事件整除。



3 实例验证
3.1 算例及参数设定

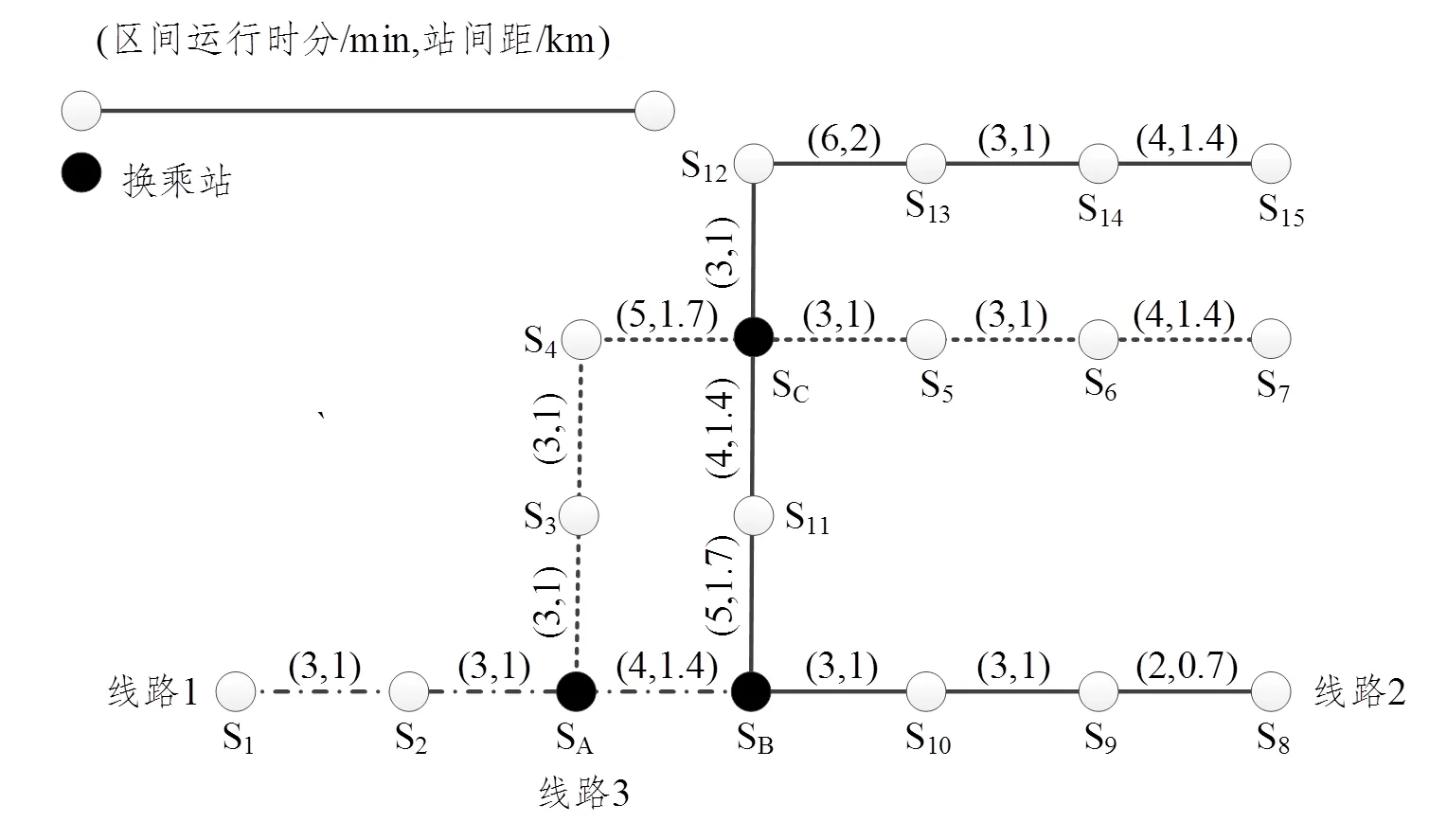
图2 实例拓扑网络图
表1 高峰小时客流OD矩阵(百人/h)

Tab.1 Passenger demand during peak hour(hundred per/hour)
表2 参数设定

Tab.2 Parameter set
3.2 计算结果
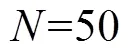

图3 遗传算法收敛过程
3.3 结果分析


Tab.3 Transfer effect for the transfer station


图4 站站台聚集人数变化情况
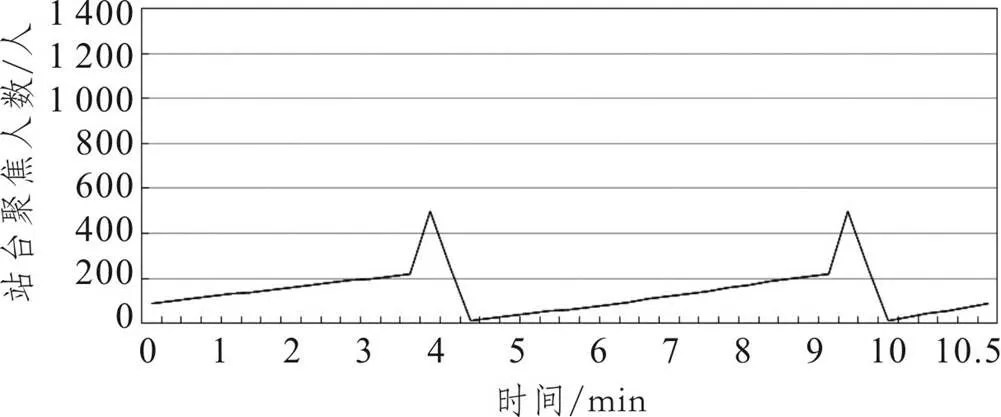
图5 站站台聚集人数变化情况
为了进一步说明本文所提出方法的有效性,采用实例中给出的客流数据和参数设置,采用文献[5]和文献[11]中所提出的模型和算法,分别计算系统总成本、列车最大载客率、站台最高容客率和乘客的总换乘等待时间等指标,与本文所提出的模型进行对比分析,结果如表4所示。其中,表4中的列车最大载客率表示区间列车载客量峰值与每列车额定容量的比值;站台最高容客率表示车站站台聚集人数峰值与站台安全容量间的比值;换乘等待总时间表示乘客在单位时间(15s)内的平均换乘等待时间。
表4 不同模型优化结果和各项指标对比

Tab.4 Comparison between results obtained using different models
注:通过文献[5]的模型进行计算时,仅考虑线路开行大交路情形,不考虑大小交路混开情形;通过文献[11]的模型进行计算时,保证列车区间运行时分和列车停站时分均不改变。
由各项指标计算情况可知,与文献[5]和文献[11]所采用的方法相比,算例中列车最大载客率分别下降了35%和38.4%,站台最高容积率分别下降了8.4%和12.2%,乘客等待总时间分别减少了5.1min和2.4min,系统总成本节省了114.1元和61.6元。说明在网络化运营条件下,考虑换乘乘客的脉冲性到达特征和拥挤度对乘客出行行为选择的影响,有利于节省城市轨道交通系统的总体优化,所提出的模型和算法具有显著优势。
4 结 论
城市轨道交通成网条件下,不同线路间乘客OD存在相互交织影响,相较于传统的单条线路列车开行方案优化,本文以城市轨道交通线网为研究对象,综合考虑各线路的发车间隔以及不同线路发车时刻的相位差,结合换乘乘客脉冲性到达特征,考虑拥挤度对乘客出行行为选择造成的影响,构建列车开行方案优化模型并求解。实例验证表明,所提出的方法能够降低运营企业运营成本,减少乘客的广义出行费用,在提高轨道交通路网运输组织效益的同时改善了乘客的服务水平。
需说明的是,由于换乘站客流聚集度较高,站台聚集人数峰值也远远高于非换乘站,易产生较大的客流压力,特别是当换乘等待时间较长时,由于客流聚集人数的不断增加,容易产生安全隐患。因此城市轨道交通运营部门应着重加强换乘站的客流组织工作,提高运输组织水平,确保运营安全。
[1] 禹丹丹, 韩宝明, 董宝田, 等. 基于换乘协同的轨道交通网列车时刻表优化模型[J]. 中国铁道科学, 2015, 36 (4): 129-135.
[2] LIEBCHEN C. The first optimized railway timetable in practice[J]. Transportation Science, 2008, 42 (4): 420-435.
[3] 汪波, 韩宝明, 牛丰, 等. 城市轨道交通网络运力优化配置研究[J]. 铁道学报, 2011, 33 (12): 9-14.
[4] 汪波, 韩宝明, 战明辉, 等. 城市轨道交通网络周期运行图编制研究[J]. 铁道学报, 2013, 35 (4): 9-15.
[5] 王永亮, 张星臣, 徐彬, 等. 城市轨道交通网络化列车开行方案优化方法[J]. 中国铁道科学, 2012, 33 (5): 120-126.
[6] 殷瑞琴, 张星臣, 陈军华, 等. 网络化运营条件下城市轨道交通末班车时刻表优化研究[J]. 铁道运输与经济, 2017, 39 (11): 103-110.
[7] TING C J, SCHONFELD P. Schedule coordination in a multiple hub transit network[J]. Journal of Urban Planning and Development, 2005, 131 (2): 112-124.
[8] IBARRA-ROJAS O J, RIOS-SOLIS Y A. Synchronization of bus timetabling[J]. Transportation Research Part B: Methodological, 2012, 46 (5): 599-614
[9] WONG R C W, YUEN T W Y, FUNG K W, et al. Optimizing timetable synchronization for rail mass transit[J]. Transportation Science, 2008, 42 (1): 57-69.
[10] SHAFAHI Y, KHANI A. A practical model for transfer optimization in a transit network: model formulations and solutions[J]. Transportation Research Part A, 2010, 44 (6): 377-389.
[11] TUZUNAKSU D, AKYOL U. Transit coordination using integer-ratio headways[J]. IEEE Transactions on Intelligent Transportation Systems, 2014, 15 (4): 1633- 1642.
[12] SERAFINI P, UKOVICH W. A mathematical model for periodic scheduling problems[J]. SIAM Journal on Discrete Mathematics, 1989, 2 (4): 550-581.
[13] BRAMSON M J, PENNYCUICK K, DAY J, et al. The instability of a close-interval service[J]. Journal of the Operational Research Society, 1957, 8 (3): 142-148.
[14] 郭金玉, 张忠彬, 孙庆云. 层次分析法的研究与应用[J]. 中国安全科学学报, 2008, 18 (5): 148-153.
[15] 项纯. 城市轨道交通投融资与建设模式的探讨[J]. 铁道工程学报, 2016, 33 (9): 118-121.
Rail Transit Optimization for Train Operation Plan under Network Operation
SUN Meng-xia,NI Shao-quan,LV Hong-xia
(1. School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 611756, China; 2. National Railway Train Diagram Research and Training Center, Southwest Jiaotong University, Chengdu 611756, China; 3. National United Engineering Laboratory of Integrated and Intelligent Transportation, Chengdu 611756, China)
To optimize the operation plan of rail transit networks, in this study, we consider the impulsive behavior of passengers on different lines, and the influence of the degree of congestion on their choice of travel. By considering the minimization of the sum of the operating cost of rail transit enterprises and the generalized travel cost of passengers as objective function, an optimization model for a train operation plan is developed. The objective is to optimize the departure interval of each line and the phase difference of the departure time between the lines. This model is combined with the discrete characteristics of passenger flow and model structure. In addition, a genetic algorithm (GA) based on simulations is utilized to solve the model. A case study of a rail transit network is considered to verify the effectiveness of the model and algorithm. The results reveal that compared with existing optimization methods, the proposed model can reduce the total cost of the system under network-operation conditions, improve the efficiency of rail transit operation enterprises, and reduce the generalized travel cost of passengers.
urban rail transit; train operation plan; genetic algorithm; departure interval; network operation
U292
A
10.3969/j.issn.1672-4747.2020.01.004
1672-4747(2020)01-0026-09
2019-01-02
国家重点研发计划资助项目(2017YFB1200702);国家自然基金项目(61703351);中国铁路总公司科技研究计划项目(P2018T001,K2018X012),四川省科技计划项目(2018RZ0078,2019JDR0211,2018123),成都市软科学研究项目(2017-RK00-00369-ZF),中央高校基本科研业务费专项资金资助项目(2682017CX022,2682017CX018)
孙梦霞(1994—),女,湖南常德人,西南交通大学硕士研究生,研究方向为运输组织优化理论与方法,E-mail: sunmengxiaa @163.com
孙梦霞,倪少权,吕红霞. 网络条件下轨道交通开行方案协调优化研究[J]. 交通运输工程与信息学报,2020,18(1):26-33, 60.
(责任编辑:李愈)

