基于客流分配的高铁票价调整策略
尹胜男,李引珍,张长泽
(兰州交通大学 交通运输学院,兰州 730070)
0 引言
随着我国高速铁路的大规模建设,长期实行单一票价策略,使得同一区段较优车次客座率接近饱和而较差车次客座率不容乐观,不仅不能调节区段不同列车间的客流分布,提升客运收益,更无法提升铁路客运服务水平从而吸引新客流,因而产生了大量的虚糜运输,造成了运力资源的浪费。根据国家发改委发布的《关于改革完善高铁动车组旅客票价政策的通知》,票价的制定权将逐步下放给中国铁路总公司,因此,改变单一票价的现状,实施合理、有效的票价调整策略将成为铁路市场化运营的必然趋势。
关于铁路票价的制定与优化问题,一直以来受到国内外学者的广泛关注。在票价制定方面,既有研究一般从单一票价[1-2]、多级票价[3-6]和动态票价[7-9]三个方面进行讨论。You[3]将客票分为全价票和折扣票两种,在需求分布已知的情况下构建非线性整数规划模型;周茵等[4]通过分析航空收益管理策略在高铁运营管理上的适用性,基于收益管理、市场细分、差别定价策略等相关理论与方法,将客运市场细分并制定差别定价的多级票价体系,但没有构建相关模型及算法;吴文娟[5]、张勇等[6]对运输通道内交通量的变化和运价率之间的关系进行分析并建立运量与运价模型,在客运专线客票折扣定价策略中引入规则引擎技术,分析不同规则下定价策略的可行性。本文将根据区段不同车次列车客座率情况制定多级票价以实现客流引导作用。
高铁票价制定过程中最重要的是广义费用的确定和票价模型的构建。在广义费用方面,Earllhart[10]将通道费用、运输费用及时间费用作为广义费用要素构建函数模型,并通过详细分析得出时间费用是其最重要的部分;史峰等[11]采用随机效用理论建立铁路旅客乘车选择行为非集计模型,给出个体旅客对列车选择概率的多项Logit模型,并通过影响因素选择及参数标定等设计求解方法。在票价模型构建方面,考虑到票价制定涉及铁路客运部门和旅客之间双层决策问题,双层规划模型成为了研究该问题的理想工具[12]。高自友等[13]基于市场经济条件分析铁路旅客票价系统,构建铁路客票定价的双层规划模型并给出求解该模型的基于灵敏度分析的启发式算法;李利华等[14]考虑物流网络需求的不确定性,利用区间参数度量不确定性变量与参数,建立区间需求模式下的物流网络双层规划模型;韦凌翔等[15]针对旅客和铁路客运部门的双重利益矛盾体提出双层规划模型,并采用内罚函数算法求解模型;李曙红等[16]建立双层规划模型用于解决高速公路网的入口流量控制问题,并提出了一种结合遗传算法和Aloplex(Genetic Algorithm and Aloplex,GAA)的新算法求解该模型。
关于票价与客流量间关系的研究,四兵锋等[17]在多模式的运输网络中应用灵敏度分析方法,提出一个多模式均衡配流模型,在此基础上,重点分析价格因素对不同运输方式客流量的影响关系;但没有考虑高铁区段车次间不同票价对于客流的影响,且仅考虑了旅客出行总需求,未考虑旅客对不同客运产品的选择行为。
基于此,本文拟从旅客出行行为分析着手,建立旅客出行广义费用函数,提出基于客流分配的票价调整策略,并构建其双层规划模型,其中上层规划根据票价调整策略构建线性规划模型,下层规划运用道路配流理论并结合高铁客运实际情况构建随机用户均衡(Stochastic User Equilibrium, SUE)模型,并在模型中加入评价旅客乘坐舒适性的路阻函数(Bureau of Public Road, BPR),同时采用基于改进Logit分配模型的相继平均法(Method of Successive Averages, MSA)[23]求解下层模型,最后结合相关案例验证该票价调整策略的可行性。
1 基于旅客出行行为分析的广义费用函数构建
1.1 旅客出行行为分析
研究铁路旅客出行选择行为需要着重考虑运输供给和旅客主观因素两大方面。铁路运输供给即铁路向旅客所提供的各种运输服务产品,评价不同运输产品需要对比不同车次列车的快速性、方便性、舒适度、运输费用等技术特征。旅客的主观选择行为是依据出行需求,结合支付能力选择符合自身喜好条件的客运产品。根据针对价格敏感度进行的意向性问卷调查[18]可知降低票价对增加出行频次有较强的正相关影响,大部分旅客面对票价降低的情况会表现出增加出行频次的倾向。利用非集计模型对价格折扣条件下的旅客出行选择[19]分析可得公差人员受票价影响较小,旅客个人出行意愿在票价折扣的情况下会明显增强。基于上述分析可知在影响旅客出行选择的众多因素中,价格因素占据至关重要的地位,票价变动会在较大程度上影响旅客的出行选择,因此,本文研究通过票价调整策略平衡区段客流,吸引新客流,提升客运收益,具有可行性。
1.2 广义费用评价指标分析
广义费用是指旅客在出行过程中所付出的代价转化为货币价值进行衡量的一种出行成本,主要包括经济性、快速性、便捷性和舒适性四大方面。
1.2.1 经济性
经济性是指旅客在接受铁路运输服务过程中所支付的货币费用,即旅客所承担的票价费用。一般而言,旅客所承担的票价费用应包括出行始发地至目的地的所有费用,但因为高铁票价费用在整个出行费用中占比较大,而在与高铁衔接的其他交通工具上所支付的费用占比较小,因此本文以高铁票价作为经济性的衡量指标,票价等于运价率与运距的乘积,而研究票价调整策略还需加入调整系数,具体计算式如下:
(1)
其中:Rk为区段s间k次列车的运价率;Lk为区段s间k次列车的旅行距离;γk为区段s间k次列车的票价浮动系数,根据《关于动车组票价有关事项的通知》中的相关规定,目前票价可以上下浮动10%,因此γk取值范围为(0.9,1.1)[8]。
1.2.2 快速性
快速性是指旅客完成出行过程所花费的时间,在广义费用计算中利用时间价值将其量化为费用。快速性费用为旅客旅行时间与时间价值的乘积,旅客时间价值采用生产法进行计算,即旅客在旅行时间内所花费的时间费用等同于在这段时间内旅客从事生产活动所能创造的价值[15],具体计算式如下:
(2)
Vt=GDP/(t×p)
(3)
其中:Vk为区段s间k次列车的平均速度;Vt为出行者的平均时间价值[20];GDP为地区国民生产总值;P为地区人口数量;t为人均年工作时间。
1.2.3 便捷性
便捷性是指旅客在整个旅行过程中乘车、换乘的方便程度。铁路旅客出行过程由出发地—始发站、始发站—终点站、终点站—目的地三部分组成。在不考虑中间站换乘的情况下,便捷性费用仅考虑车站所在市区范围内出发地—始发站和终到站—目的地两部分的乘车方便程度。完成以上出行可以采用公交车、地铁、出租车和私家车四种方式。在广义费用中计算便捷性时,参考公交、地铁日常运营时间以及一天中客流高峰与低峰时段,将24 h划分为不同的时间段并进行聚类分析,依据选择4种交通方式的旅客人数比例计算不同时间段的平均费用以衡量不同高铁车次的便捷性指标。具体计算式如下:
(4)
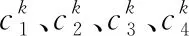
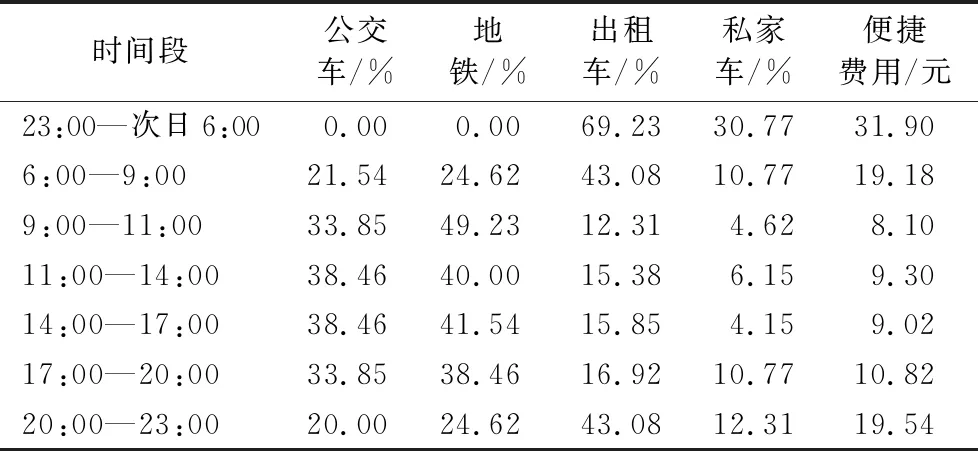
表1 不同时段旅客出行便捷性广义费用 Tab. 1 Convenience cost for passengers in different periods
1.2.4 舒适性
舒适性是评价客运产品服务质量的关键因素。根据现有研究,舒适性是以旅客完成旅行后疲劳恢复所需的时间进行衡量[23]。旅客舒适性费用与旅行时间是成正比的,旅行时间越长,疲劳恢复时间越久,舒适性越差;反之,则舒适性越好,因此计算舒适性费用首先需要计算出疲劳恢复时间,然后采用时间价值计算方法将其转化为费用,其中疲劳恢复时间与旅行时间和列车环境有关,舒适性相关计算式如下:
(5)
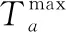
2 双层规划模型构建
2.1 模型介绍
高铁票价制定需要综合考虑客运管理部门和旅客双方利益,其两者之间是典型的Leader-Follower关系,即高铁客运管理部门为决策指导者(Leader),旅客出行选择行为为跟随者(Follower)。高铁运输部门可以通过实施票价调整策略优化旅客广义出行费用,影响旅客的出行选择,但是不能控制其选择行为。出行者通过对已有的多种出行方式对比分析,结合自身的出行需求选择最理想的出行方式[15]。基于此,本文通过构建双层规划模型描述票价制定双方间的关系。
2.2 模型建立
2.2.1 上层规划模型
上层规划是从高铁客运部门的角度出发,构建以客运收益最大化为目标的线性规划模型。上层规划模型(U)如下:
(6)
s.t.apk≤pk≤bpk
(7)
0.6≤Rk≤0.9
(8)
Rk=fk/ck
(9)
上述模型中:式(6)为目标函数,表示客运收益最大化;式(7)为票价调整限制约束;式(8)为列车客座率限制约束,根据现有研究,高铁全年总客座率在73%左右,其中淡季全日总客座率大约在60%左右[19],为保证高铁最低客运收益,同时达到平衡区段客流的目的,本文取列车客座率的合理分布范围为(0.6,0.9);式(9)为客座率表达式。pk为区段s间k次列车的票价;a,b为票价调整系数,依据文献[8]分别取值为0.9和1.1;ck为区段s间k次列车的定员;fk为区段s间k次列车实际客流量,其中fk是由下层规划模型求出;Rk为区段s间k次列车的客座率。
2.2.2 下层规划模型
下层规划模型从旅客角度出发,构建以旅客广义出行费用最小化为目标的SUE模型。结合高铁客运的实际情况,本文不考虑中转换乘的情况。下层规划模型(L)如下:
(10)
s.t. 0≤fk≤ck
(11)
(12)
上述模型中:式(10)为目标函数,其中前半部分控制SUE模型的随机性,后半部分为旅客广义出行费用最小化;式(11)为列车旅客容量约束,即旅客量要满足非负约束并且小于列车定员;式(12)为总量平衡约束。θ是非负的校正参数,可以用来调整SUE模型的随机性,依据文献[22]取值为0.5;Qs为区段s间的出行需求总量;Rs为区段s间列车车次的集合;Tk(f)为区段s间k次列车客流量为f时的BPR阻抗函数,具体表示如下:
(13)

(14)
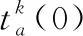
在上述双层规划模型中,上层决策者根据票价调整策略设置区段不同车次列车的票价值并影响下层决策者对路段阻抗值的理解,从而限制了下层决策者的可行约束集,即铁路旅客票价的制定策略直接影响旅客的出行选择,而区段内不同车次间客流分布反过来也会影响票价策略的制定,所以上层规划的决策变量与下层规划的决策变量是相互作用的。
3 算法设计
票价调整双层规划模型的算法设计包括票价调整方案制定和双层规划模型求解两部分。本文首先设计票价调整策略,然后依据调整策略制定票价调整方案,最后在不同的方案下求解双层规划模型。
3.1 票价调整策略
票价调整策略是在合理的票价调整范围内将区段间不同车次列车按照客座率指标进行归类,为保证列车最低客座率在60%以上,同时避免客座率达到100%,因此本文在客座率区间(60%,100%)对称选取两条票价调整点,将客座率高于85%的列车票价上调,客座率低于75%的列车票价下调,从而引导、控制客流,使区段内各列车客座率分布在理想区间(60%,90%),但是票价上调或下调先后顺序、调整幅度的不同组合对客流的均衡效果以及客运收益的影响是不同的,因此,本文将票价调整方案分为以下三种,如表2所示。

表2 票价调整方案 Tab. 2 Fare adjustment schemes
3.2 双层规划求解算法
3.2.1 SUE模型解的唯一性证明
(15)
(16)
由式(16)可以看出,Hessian矩阵是正定的且该SUE模型为严格凸规划[22],所以模型存在唯一最优解。
3.2.2 求解算法设计
双层规划模型的求解是NP难问题(Non-deterministic Polynomial hard,NP-hard),非凸特性是求解该问题的难点[21],因此,求解的关键是找到上层规划模型与下层规划模型间的反应函数,即客流量与票价间的函数关系。基于此,本文首先求解下层模型,得到当前票价下的客流分配情况,然后代入上层模型中求解当前客运收益值,并按照票价调整方案更新票价值代入下层模型中,依次循环,直至得到客运收益最大值下的票价组合,算法结束。模型求解的具体步骤如下。
步骤1 计算客座率。根据各车次列车客流量计算客座率,并分别标记客座率Rk小于75%的车次kx和客座率Rk大于85%的车次kg以及客座率Rk在75%~85%的车次kz。
步骤2 选定票价调整方案并制定票价变动规则,三种票价方案对应的票价变动规则如表3所示。
步骤3 客流分配。更新票价Pk代入下层SUE模型并采用MSA求解,得到各车次的客流量fk,具体步骤如下:
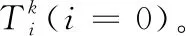
本课程的教学创新体现在以下几个方面:(1)教学过程充分利用网络资源、运用蓝墨云班课等App学生的移动设备变成学习工具;(2)课程教学注重文化熏陶,素养培养贯穿教学过程;(3)课证融合、课赛结合,提高了学生的学习积极性,有效提高了教学效果。(4)全过程学习成效评价,通过云班课记录的学生学习行为实现对学生的过程性考核,完善的激励与评价体系促使学生在移动设备端的自主学习,激发了学生的自主学习兴趣。
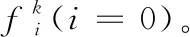
(17)
4)迭代。用加权平均的方法计算区段s间各车次当前的旅客量:
(18)
5)收敛判断。若当前的迭代次数小于给定的迭代次数N时,令i=i+1并返回步骤3;否则停止迭代。
步骤4 更新客运收益值。若各车次的客座率满足在区间(60%,90%)内即更新最大客运收益值w并记录下最大客运收益下各车次的票价Pk和旅客量fk,转步骤1。
步骤5 迭代停止。当票价调整方案满足票价调整结束条件时,即停止迭代。

表3 票价调整策略 Tab. 3 Fare adjustment strategy
4 算例分析
表4为某一固定区段内的各车次列车信息表,该区段内各车次列车均为始发终到列车,定员均为600,为了方便计算,以二等座票价代替高铁票价。根据票额分配的相关制度,客座率根据该列车在该区段上所分配的票额数量计算,假定全程票票额数量为列车定员的67%,按照高铁票价的变化浮动范围,该区段票价浮动区间为(477,583)元。应用Matlab R2018a在Windows 7平台下实现上述求解算法。在求解SUE模型时,将迭代步数N设置为1 000,采用票价调整策略的三种方案对算例票价进行调整,并对不同方案下的客运收益、客座率结果、旅客出行成本进行分析,计算结果见表5~7所示。
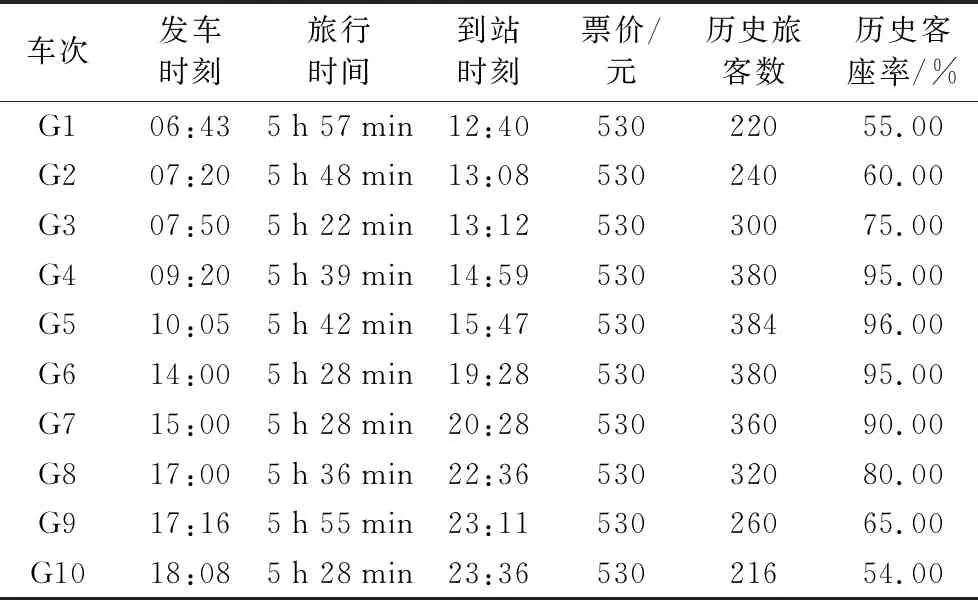
表4 区段各车次列车信息 Tab. 4 Information of different trains in a section

表5 票价调整方案收益 Tab. 5 Revenues of different fare adjustment schemes
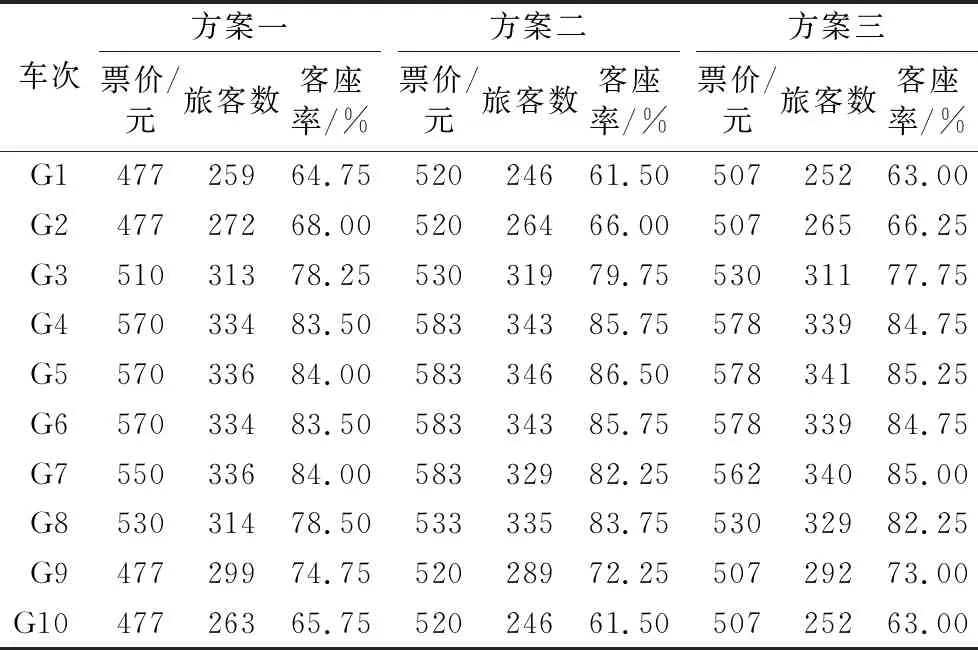
表6 票价方案调整结果 Tab. 6 Results of fare adjustment schemes
高铁票价调整策略是为了实现客运收益的提升、均衡区段列车客流、降低旅客出行成本三重目标,因此本文从上述三个方面对三种票价方案的调整结果进行对比分析。
1)客运收益分析。
分别绘制3种方案调整过程中的收益迭代图,如图1所示。
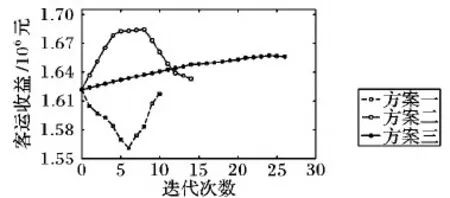
图1 客运收益迭代Fig. 1 Iteration graph of passenger transport revenue
由图中3种方案的客运收益迭代曲线看,方案二和方案三调整过程中的客运收益都较未采取调整措施前高,并且调整结束后都实现了提升客运收益的目的。对比这两种方案,方案二的收益提升率高于方案三,并且能够在较少的迭代次数内得到最大的客运收益。相比之下,方案一调整后的最大客运收益仍低于未调整前,这是因为该方案采用先降价后上调的调整顺序,降价过程中客运收益开始下降直到达到票价下限值后上调票价,票价上调过程中客运收益逐渐提升,但未达到票价上调上限值时就已经满足了客座率目标区间,因此调整后的客运收益低于方案二和方案三。
2)列车客座率分析。
分别绘制采用票价调整方案前后各车次客座率曲线,如图2所示。
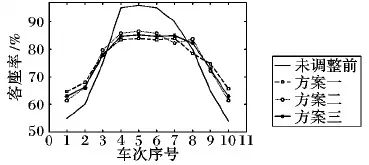
图2 票价调整前后客座率对比Fig. 2 Comparison of passenger load factor before and after fare adjustment
由图2票价调整前后各车次客座率曲线看,三种票价调整方案较未调整前都能很好地均衡区段客流,使得同一区段不同车次列车客座率不至于出现畸高或畸低现象,避免旅客在较优车次列车临近发车时买不到到车票而选择其他交通方式,从而减少铁路客流的损失。对比三种票价调整方案,总体来说三种方案的调整效果相差不大,车次较优的列车客座率平均下降了10个百分点,车次较差的列车客座率平均提高了7.8个百分点。其中方案一的客座率曲线图更平稳,各车次列车客座率分布更均衡,这是因为采用先降价的票价调整策略会刺激旅客选择降价车次,并且在票价调整过程中前期刺激引导作用远大于后期,因此方案一在客座率调整方面更具优势。
3)旅客出行成本分析。
分别计算三种方案调整后的旅客出行成本,并与未调整前的出行成本进行对比,结果如表7所示。
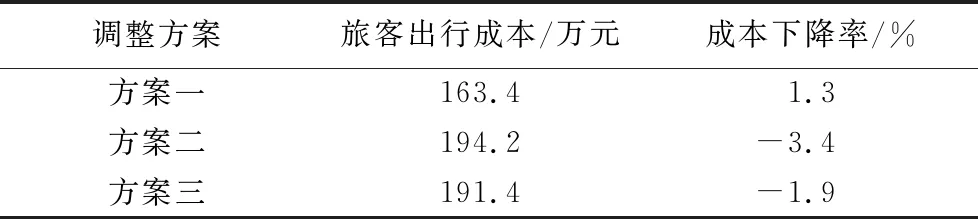
表7 旅客出行成本分析 Tab. 7 Passenger travel cost analysis
由表中数据结果可知,采用方案一对票价进行调整能够降低旅客的出行成本,而方案二和方案三无法达到该效果。这是因为在旅客出行成本中高铁票价占绝大部分比重,方案一先降价后上调的顺序使得票价能够达到票价调整下限值而无法达到票价调整上限值,因此使得总体客票价格下降,旅客出行成本随之下降。相比之下,方案二和方案三调整后的票价总值均较未调整前的高,所以无法降低旅客的出行成本。
综合分析发现,方案一适用于客流量接近饱和的高峰时期,例如双休日等,这是因为该时期客运收益远远大于运输成本,提升客运收益不再是最主要的目的,合理地引导、均衡客流,提高区段各车次列车客座率,充分利用运能资源成为关键,并且方案一能够降低旅客的出行成本,因此在一定程度上也可以提升高铁的竞争力,减少客流损失现象。方案二和方案三适用于非高峰时期的旅客运输,这是因为该时期客座率普遍较低,旅客流失现象较高峰时期有所减少,提升客运收益成为该时期的主要目的,这两种方案既能够较大程度地提升客运收益,也能很好地调节客流分布。
5 结语
本文以高铁实行单一票价为实际背景,提出基于客流分配的票价调整策略,制定票价调整方案,构建票价调整双层规划模型,并设计相应算法求解该模型,最后通过算例对模型和算法进行验证,结果表明:
1)本文在分析旅客广义出行费用中的便捷性评价指标时对时间进行聚类分析,对比不同时间段旅客乘坐公交、出租车、私家车以及地铁的便利程度并将其转换为便捷性费用,能够将旅客旅行的衔接便捷性准确地表现在广义费用函数中。
2)为了实现票价调整的三重目标,本文构建了票价调整双层规划模型,其中BPR函数的建立准确地表示出客流量分配与票价之间的关系,实现上层模型与下层模型间的紧密联系,因此,该票价调整模型能够符合高铁运营的实际情况,具备现实可借鉴性。
3)根据票价调整策略制定三种票价调整方案,通过算例对三种方案在客运收益提升方面、区段客流均衡分配方面、旅客出行成本方面的优化效果进行分析,结果表明:方案一能够有效地满足客流高峰期对均衡客流的需求;方案二和方案三可以实现在客流非高峰时期提升客运收益的目的,为铁路客运管理部门优化票价体系提供参考依据。
本文仅依据票价调整策略提出三种票价调整方案,但实际票价调整方案种类较多,票价调整先后顺序及调整幅度的多重组合可以形成不同的票价调整方案,因此不同调整方案对于区段客流分配、客运收益、旅客出行成本的影响还有待深入研究。

