基于近邻传播聚类和TANE算法的高校数据中函数依赖的发现
黄永鑫,唐雪飞
(电子科技大学 信息与软件工程学院,成都 610054)
0 引言
高校信息化经过多年的发展,很多高校已积累了大量的业务和相关数据,数据不同于有形的产品,但同样具有质量这一概念,但是因为数据质量不高、冗余数据大量存在和数据可用性不高,使很多数据处理工作还需要通过人工来确保正确,浪费了大量的人力和时间[1]。
我国教育领域已初步解决数据的有无问题。然而,大量数据仍未得以充分应用,究其原因,除了教育工作者对数据价值重视不够等主观原因外,数据质量不高、数据状态不能适应当前教育发展也是重要的客观原因[2]。
数据缺失是数据质量问题的其中一种,在高校数据中,比如对于学工系统中的数据来说,造成数据缺失的原因可能是由于人工录入失误,也可能是在数据传输过程中造成了缺失。大量缺失值将使得从数据中发现出的数据质量检测规则不准确,使得领域专家无法根据发现出的数据质量检测规则有效修复数据集中存在的脏数据等问题。若直接将含有缺失值的数据删掉,会使得数据集中丢失的数据较多,进而使得基于该数据集所作出的数据分析结果产生较大偏差。
在高校信息化建设的过程中,通过开展高校数据治理以提高数据质量,可以有效提高数据价值,为组织决策的制定提供帮助。同时,通过对高校信息化建设中数据治理的研究,可以认清在高校信息化中存在的问题,有效促进我国高校信息化的建设[1]。函数依赖(Functional Dependency, FD)这一概念首先在文献[3]中被研究,它表征的是数据实例中字段之间的关联关系,可以作为数据治理的检测规则以提升高校数据的数据质量。对于函数依赖的发现包括了发现一个给定关系中的函数依赖、多值依赖以及近似函数依赖[4-6],而用于发现函数依赖的算法主要有:TANE[7]、FUN[8]、FD_MINE[9]、DFD[10]、DEP-MINER[5]、FASTFDS[6]、FDEP[11]等,这几种算法可以被分成三类:第一类为属性格遍历算法,包含TANE、FUN、FD_MINE和DFD四种算法[12]。TANE、FUN和FD_MINE使用了基于apriori-gen候选生成原理的自下而上的遍历策略[13],DFD实现了深度随机游走。虽然遍历策略各不相同,但这四种算法都会连续生成新的候选函数依赖并使用精简分区来单独验证它们。本类中的所有算法都使用并扩展了TANE算法的剪枝规则。第二类为差异-一致集算法,包含DEP-MINER、FASTFDS。第三类为依赖推理算法。
在这几种算法中,最著名的就是文献[7]中提出的基于层次搜索属性包含格的TANE算法,该算法在元组数较大的情况下表现良好并且相对于属性格遍历算法中的其他算法,该算法在属性进行横向扩展时的表现也更好,因此,结合高校实际数据元组数较大、属性个数较多的特点,本文选择TANE算法来自动发现函数依赖;但由于在进行函数依赖的自动发现时,真实的高校数据集中存在的大量缺失值会使得经过TANE算法发现出的函数依赖不准确,若直接使用这些函数依赖来进行脏数据的修复,将可能使得数据集中的脏数据变得更多,影响学校领导、老师的决策,本文提出了一种使用近邻传播(Affinity Propagation, AP)聚类算法和TANE算法结合的先进行缺失值填补,然后在不含缺失值的数据集上发现出函数依赖的APTANE方法。这一方法在之前的研究过程中并未受到关注,它有效解决了高校数据因存在大量缺失值使得从数据集中发现出的函数依赖不准确,影响学校领导、老师作出进一步决策等问题。
1 基本概念
1.1 数据质量维度
数据和信息质量思想家都采用了维度(dimension)一词来确定可以测量数据的哪些方面[14]。虽然不同的专家提出了不同的数据质量维度,但是几乎都离不开完整性、完备性、一致性、有效性和及时性这五大维度。
完整性 完整性衡量的是数据所拥有的完整程度,它指的是未分割的整个状态或统一的状况[14]。该维度体现了对基本数据的质量测量。可以通过检测规则来保证数据完整性,而检测规则可以通过领域专家制定或从数据集中自动发现的方式来获得,如本文使用TANE算法发现出的函数依赖就是一组检测规则。
完备性 完备性衡量的是数据所拥有的广度、宽度以及深度。数据的广度指的是模式所具有的字段数,数据的宽度指的是字段值的填充情况,而数据的深度则指的是模式所具有的数据条数。
一致性 一致性衡量的是字段、数据含义均相同的数据的一致程度[14]。在数据集合中,指的是每个信息都不包含语义错误或相互矛盾的数据[15]。例如某些考评结果,有的是优、良、差,有的是甲、乙、丙,这就造成了数据度量的不一致,因此满足一致性是进行数据集成的基础[1]。
有效性 有效性是数据对一组业务规则的符合程度,有时被表达为一个标准,或在已定义的数据域中被表示。它是数据对数据标准、数据模型、业务规则、元数据和参考数据等的符合程度。例如,将输入数据的值与某个数据标准的有效值进行比较[1],就是对输入数据有效性的检验。
及时性 及时性衡量的是存储在系统中的数据与真实数据相比的更新程度。及时性可相对于某个设定的计划,或某个事件的发生来测量。例如,及时性是数据从源系统交付时对交付计划的符合程度[14]。
1.2 AP聚类算法
AP聚类算法是2007年Clustering by Passing Messages Between Data Points[16]一文中提出的一种新的聚类算法。该算法在执行之前不需要定义聚类的类数,算法通过在迭代过程中不断搜索合适的聚类中心,自动从数据点间识别类中心(Exemplars)的位置及个数,使所有的数据点到最近的类代表点的相似度之和最大[17]。算法最开始将所有的数据点都视为聚类中心,并基于数据点之间的信息传递来实现聚类过程。
与一般的聚类算法,比如k-means算法相比,由于AP聚类算法在运算开始前不需要指定聚类的簇数,使得先验经验不是必需的;除此之外,数据集样本中所有的数据点都可能成为AP算法的核,而不是像k-means等算法是通过求平均的方式来获得聚类中心;由于k-means聚类算法需要人工设定簇数,且多次运算的结果可能不同,因此会影响聚类效果,导致聚类结果不稳定,而AP聚类算法多次执行后,每次的结果是完全相同的,因此聚类结果相对于k-means等一般的聚类算法来说更加稳定。目前为止,AP聚类算法已经被应用到了多个领域,如图像识别、文本挖掘等,均取得了较好的效果[18-20]。
在AP聚类算法中,消息的传递是通过更新代表信息矩阵R(Responsibility)和选择信息矩阵A(Availability)来进行的。代表信息矩阵中的元素r(i,k)表征的是数据点k适合作为数据点i的聚类中心的程度,如图1所示,它代表了从点i到点k的消息,而选择信息矩阵中的元素a(i,k)表征的是数据点i选择数据点k作为其聚类中心的适合程度,如图2所示,它代表了从点k到点i的消息。
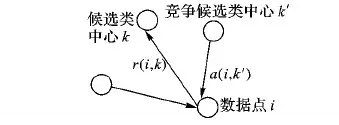
图1 代表信息的更新过程Fig. 1 Update process of responsibilities
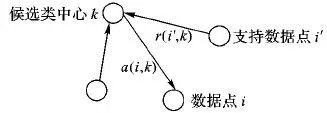
图2 选择信息的更新过程Fig. 2 Update process of availabilities
要更新代表信息矩阵R和选择信息矩阵A需要对任意数据点i计算其他所有数据点k与点i的r(i,k)和a(i,k)。在算法初始化时,令a(i,k)=0,可以通过式(1)、(2)来分别计算r(i,k)和a(i,k):
r(i,k)=s(i,k)-max[a(i,k′)+s(i,k′)];k′≠k
(1)
a(i,k)=
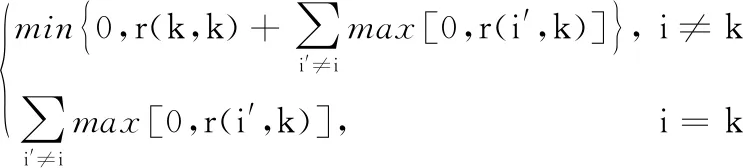
(2)
需要注意的是,a(i,k′)和s(i,k′)代表的是上一次的迭代更新结果。由式(1)和(2)可以得到r(i,k)与a(i,k)的和,即式(3):
r(i,k)+a(i,k)=s(i,k)+a(i,k)-
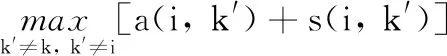
(3)
对于数据点i,若r(i,k)与a(i,k)的和最大,则数据点k即为类中心,当r(i,k)与a(i,k)的和在迭代过程中保持不变时,消息的传递过程结束。
1.3 函数依赖
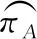
关系R上的函数依赖可以表示成X→A的形式,其中,X是给定关系R中的属性集,A是R上的某个属性,A的值唯一地由X的值决定。对于一个形如X→A的函数依赖,属性集X称为该函数依赖的左部,而属性A称为右部。为了保证发现的函数依赖是有意义且非冗余的,要求发现出的函数依赖必须满足非平凡和最小这两个条件。非平凡函数依赖指的是:属性A不属于属性集X,即:X
1.3.1 分区
在给定关系R中,属性X的分区可以用πX来表示,πX={[t]X|t∈r},其中,[t]X为分区πX中的等价类,可表示为:[t]X={u∈r|t[A]=u[A]}[4],其中,A∈X。
对于数据表中的某个字段,将具有相同字段值的元素归为同一个等价类,这样,该字段具有多少个不同值,对应的分区中就有多少个等价类。比如,在表1所示的学生信息实例中,字段“专业”的分区为:π专业={{1,6,7,8},{2,4},{3},{5}}。
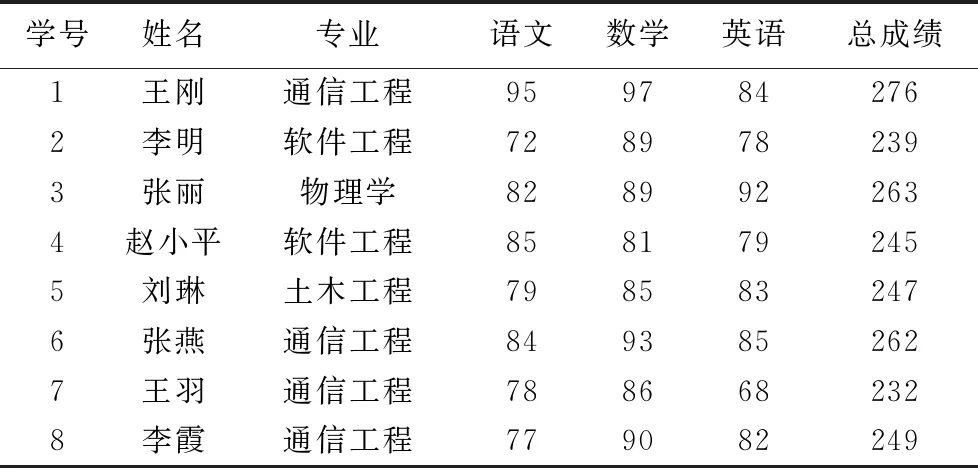
表1 学生信息实例 Tab. 1 Examples of student information
1.3.2 精炼分区
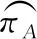
1.3.3 右部集
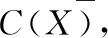
为了找到最小的函数依赖,需要对属于属性集X并且对于所有属于属性集X的属性B,检测XA}→A是否满足,其中,A∈C(XB})。
1.3.4 超键
如果任何两个元组在属性集X上的值都不等,那么属性集X就是一个超键。令B∈X,并且令XB}→B是一个有效的依赖,此时,如果X是一个超键,那么XB}也是一个超键。通常,在X∪{A}被处理时需要测试X→A(A∉X)是否成立,这就需要使用πX∪{A}来进行有效性测试,然而,如果X是超键,那么X→A将始终有效,因此可以不再额外使用πX∪{A}来进行有效性测试。
1.3.5 剪枝
对TANE的搜索空间进行剪枝可以基于:如果C(X)=∅,那么C(Y)=∅,其中Y是X的超集。也就是说,如果XA}→A是最小的函数依赖,则不会再有形如YA}→A的函数依赖是最小的函数依赖,集合Y也不会再被处理,因此Y可以被剪掉。
2 方法流程及相关算法介绍
由于在研究使用TANE算法从高校数据中发现函数依赖时,数据表中存在的缺失值使得发现的函数依赖个数较少,且所表征的字段间的关联关系不准确,因此本文针对这一问题,提出使用AP聚类算法和TANE算法结合来发现高校数据中函数依赖的APTANE方法。首先介绍本方法的具体流程:1)在数据预处理阶段,若待测字段中含有中文字段,则首先对该字段的中文字段值进行列剖析,用该中文字段值在该列中出现的次数来替换对应中文字段值;2)使用AP聚类算法对待测字段中包含有缺失字段值的字段进行缺失值填补;3)在经过上述步骤处理后的不含缺失值的数据集上使用TANE算法自动发现满足非平凡、最小要求的函数依赖。下面对该方法中涉及到的已有算法进行简要介绍。
2.1 进行缺失值填补的AP聚类算法
在自动发现函数依赖之前,首先使用AP聚类算法对高校数据集当中所选字段存在的缺失值进行填补。下面对该过程使用算法1进行描述。
算法1 AP_For_Filling_Missing_Values。
输入:待修复数据集,阻尼系数和最大迭代次数。
输出:已进行缺失值填补的数据集。
初始化λ,maxIterNum,计算相似度矩阵S
setChineseToNum()
setPreference()
Fori:=0 TomaxIterNum
updateResponsibility()
updateAvailability()
End For
assignClusterPoint()
setPredictValue()
setNewValue()
AP聚类算法首先需要设定阻尼系数λ和最大迭代次数maxIterNum的值,以初始化算法,并计算相似度矩阵S,相似度矩阵S中的元素s(i,j)表征的是数据点i,j之间的相似度,使用欧几里得距离计算公式得出,即:s(i,j)=-‖xi-xj‖2。使用AP聚类算法来进行缺失值填补时,由于高校数据中可能存在中文字段,而AP聚类算法在计算两点之间的相似度时无法直接对中文字段值进行处理,因此本算法使用了setChineseToNum()方法将中文字段值替换成对应的数值,然后再进行聚类的后续步骤。setChineseToNum()方法通过计算中文字段中不同字段值出现的次数,以此来替换原有值。
算法1使用setPreference()方法来设定参考度Preference的值。Preference指的是点i作为聚类中心的参考度(不能为0),表示为p(i)或s(i,i),取值为S对角线的值,此值越大,作为聚类中心的可能性就越大。Preference的值决定了AP聚类算法输出的类别,在无先验知识的情况下,所有数据点都可以看成是潜在的聚类中心代表。
AP聚类算法迭代过程的核心是两个信息矩阵的交替更新过程。首先应计算样本点间的r(i,k)和a(i,k)。样本点间的r(i,k)的计算方法为:
样本点间的a(i,k)的计算方法为:
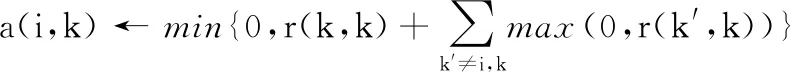
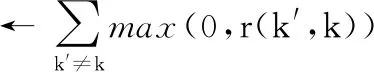
在计算了样本点间的r(i,k)和a(i,k)之后,算法1使用式(4)、(5)来分别更新代表信息矩阵和选择信息矩阵:
rt+1(i,k)=λ*rt(i,k)+(1-λ)*rt+1(i,k)
(4)
at+1(i,k)=λ*at(i,k)+(1-λ)*at+1(i,k)
(5)
在AP算法实现的过程中任何点的r(i,k)和a(i,k)都与定义聚类中心相关联。对于a(i,k)+r(i,k)取最大值时的k值,如果k=i,则将数据点i作为聚类中心,否则将数据点k作为点i的聚类中心。
assignClusterPoint()方法用于将各数据点分配到聚类中心所在的类中。若迭代次数超过设定的最大值或者当聚类中心在若干次迭代过程中不再发生改变,则停止计算,得出最终的聚类中心及各个类所拥有的样本点。setPredictValue()方法用于得到AP聚类算法对于缺失值的预测值,setNewValue()方法用于将数据集的缺失值填补为AP聚类算法所预测出的值以得到经过AP聚类算法处理后的不含缺失值的数据集,以便进行后续从数据集中自动发现函数依赖的步骤。
2.2 发现函数依赖的TANE算法
从数据集中自动发现字段之间的关联关系,可以减少领域专家配置数据质量检测规则的工作量,提高工作效率;并且,自动产生的数据质量检测规则可以作为进一步检测脏数据的指标,提升高校数据所拥有的数据质量。本文使用TANE算法从已进行了缺失值填补的数据集上自动发现函数依赖。从文献[7]可知,该算法使用的是基于层次搜索属性包含格的方法,算法首先从空集开始,向下生成属性集,然后在当前层计算候选函数依赖,对候选函数依赖进行非平凡性和最小性的检测,剪掉不满足要求的节点,节约搜索空间,然后继续从当前层生成下一层,重复以上过程,直到找出所有满足要求的函数依赖。当算法在处理每一层的属性集X时,它会检测形如XA}→A(A∈X)的函数依赖是否成立,这就可以保证只有非平凡的函数依赖会被考虑。另外,算法由小到大的扩展方向可以保证只有最小的函数依赖被输出,并且由于TANE算法基于的是上一层的结果来生成下一层的属性集,也减小了相应的计算量。下面对算法2 TANE算法进行详细描述。
算法2 TANE。
输入:已进行缺失值填补的数据集。
输出:数据集上存在的非平凡、最小函数依赖。
L0:={∅}
C+(∅):=R
L1:={{A}|A∈R}
l:=1
whileLl≠∅
compute_dependencies(Ll)
prune(Ll)
Ll+1:=generate_next_level(Ll)
l:=l+1
TANE算法首先令第L0层为空集,然后从L1={{A}|A∈R}开始,由第L1层计算出第L2层,由第L2层计算出第L3层,以此类推。当第Ll层不为空时,使用compute_dependencies(Ll)方法来计算该层的候选函数依赖。方法为:对于第Ll层中的每个属性集X先计算C+(X)。要得到C+(X),需要先计算C+(XA}),此处的属性A是属性集X中的单一属性,然后把计算出的结果取交集,即可得到C+(X)。对于每一个属于X∩C+(X)集合中的属性A,如果XA}→A是有效的,则输出XA}→A这一候选函数依赖,并且从C+(X)中移除属性A,从C+(X)中移除所有属于RX集合的属性B。
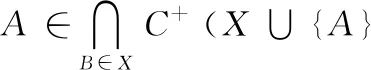
使用generate_next_level(Ll)可以从第Ll层生成第Ll+1层。首先令Ll+1这一层为空集,对于Ll这一层中的每一个前缀块K进行如下操作:对于每一对包含于前缀块K中的两个不同的属性集Y、Z,将Y∪Z的结果赋给X,并判断如果对于所有属于属性集X中的属性A,都有从X中去掉属性A之后,余下的属性仍然属于第Ll层这一结果,那么就将Ll+1∪{X}的结果赋给Ll+1,以生成第Ll+1层。当找出了给定的已进行缺失值填补的数据集上存在的所有满足非平凡、最小条件的函数依赖之后,算法会终止,不再继续生成下一层。
3 实验结果及分析
本实验的运行环境为使用Intel酷睿i7- 3.2 GHz的CPU,16 GB内存的Windows计算机,实验使用的数据集分为测试数据集和真实数据集。测试数据集来自UCI数据集的breast-cancer-Wisconsin数据集,包含肿块厚度、细胞大小均匀性、细胞形状均匀性、类别等11个属性,共有699条元组。使用breast-cancer-Wisconsin数据集的原因在于该数据集的属性之间存在着一定的关联关系,便于进行函数依赖自动发现这一过程。表2为该数据集的字段信息。
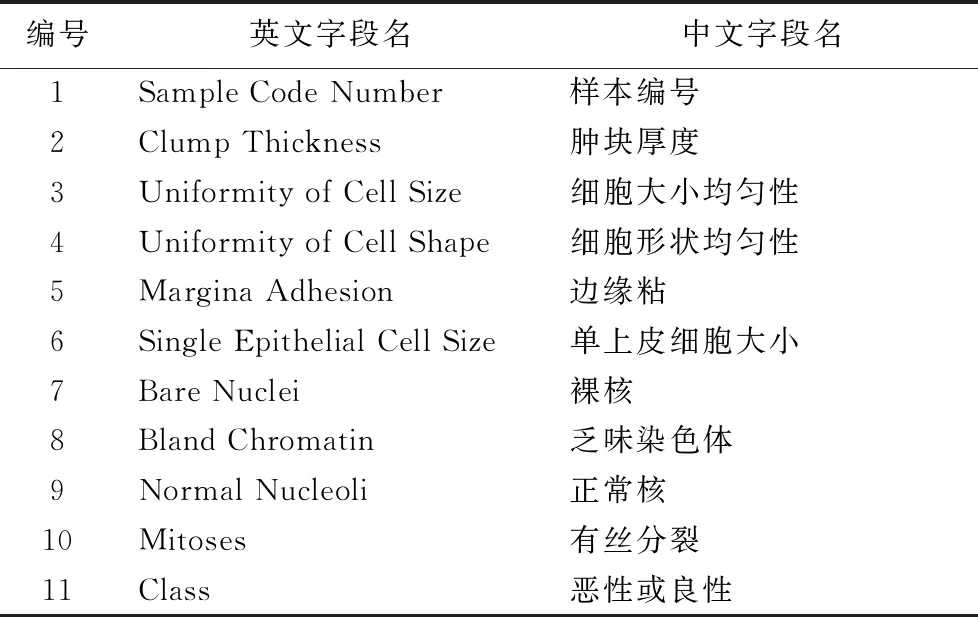
表2 breast-cancer-Wisconsin数据集字段信息 Tab. 2 Field information of Breast-cancer-Wisconsin dataset
真实数据集来自某高校学生信息数据集,共有30 648条元组,是用学生信息表以及贫困补助表两者进行合并形成的数据集。表3为该数据集的字段信息。
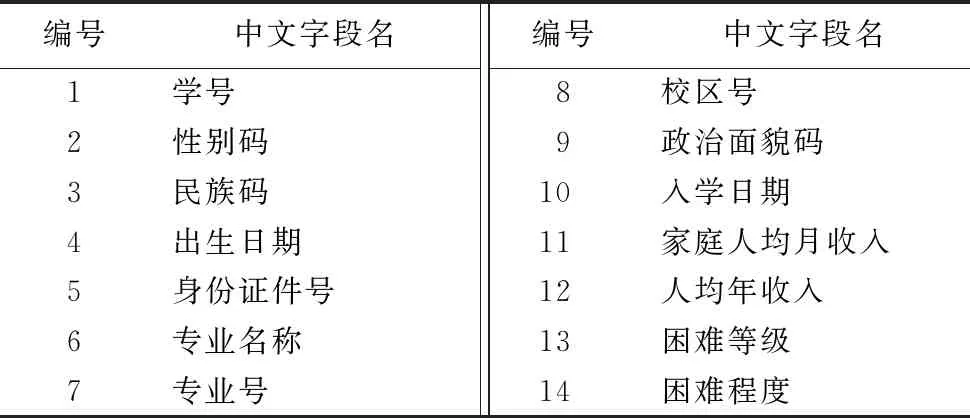
表3 高校数据集字段信息 Tab. 3 Field information of university dataset
由于使用的测试数据集breast-cancer-Wisconsin不包含空值,因此,为了检测使用AP聚类算法来进行缺失值填补之后能提升TANE算法所检测出的函数依赖的个数和准确度的可行性和有效性,采用了通过设定不同缺失率e向数据集中注入n*e个空值由此来形成含有空值的数据集,并在此数据集上进行测试数据集缺失值填补实验的方式。其中,n为元组个数。
图3显示了在缺失率e的取值分别为0.02、0.04、0.06、0.08时AP聚类算法填补测试数据集上的缺失值的准确率,可以看出,缺失值填补的准确率随着e值的增大呈现平稳增长的趋势,在e大于等于0.04时维持在较高水平,并且在缺失率为0.06时,使用AP聚类算法填补缺失值的准确率最高,为94.87%,在缺失率为0.08时,由于字段值缺失数增加使得最近邻点以及近邻区域对聚类代表点产生了影响,导致准确率有所下降,但仍然保持在90%以上。
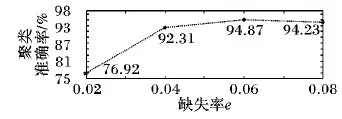
图3 聚类准确率随e值的变化Fig. 3 Clustering accuracy changing withe value
图4是在测试数据集上将本文的APTANE方法分别与TANE、DFD、FUN算法所发现出的函数依赖个数的对比。
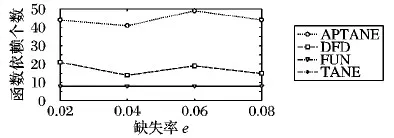
图4 不同缺失率下的各算法发现的FDs个数Fig. 4 Number of FDs found by each algorithm under different missing rates
TANE、DFD和FUN算法都是基于属性格的遍历来发现函数依赖的方法,它们在具有大量元组数的数据集上表现比差异-一致集算法以及依赖推理算法更好[11],因此本文根据实际应用场景中高校真实数据集的特点选择将APTANE方法与TANE、DFD、FUN算法进行比较。从图4可以看出:在不处理缺失值,直接从原始数据集上使用TANE、DFD、FUN这三个算法时,发现的函数依赖个数较少,三个算法中,DFD算法能发现的函数依赖最多为21个,而FUN算法和TANE算法不管缺失率的值如何变化,均只能发现8个;而本文提出的APTANE方法由于对数据集中的缺失值进行了填补,完善了字段值之间隐藏的关联信息,因此能发现出更多的函数依赖,并且个数接近于测试数据集不存在空值时所发现出的46个函数依赖。
从表4测试数据集不存在缺失值以及缺失率为0.06时APTANE所发现的FDs的对比中可以看出,在e为0.06时所发现出的FDs完全覆盖了不存在缺失值的情况下所发现的所有FDs,结合图3准确率的增长趋势,表明了在聚类准确率越高的情况下,所发现的FDs越准确、越完整。本文使用的高校真实数据集是存在大量缺失值的数据集,存在的缺失值主要集中在”困难程度”字段。图5是在高校真实数据集上将本文的APTANE方法分别与TANE、DFD、FUN算法所发现出的函数依赖个数进行对比后得出的结果。
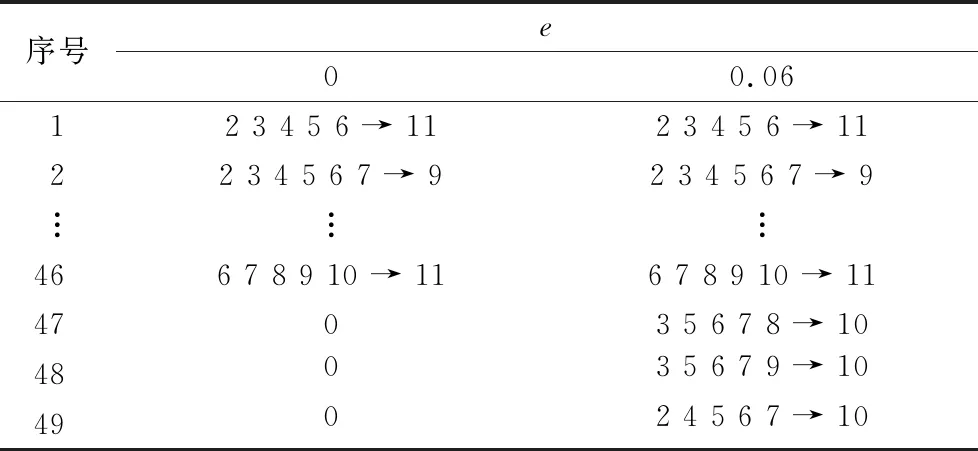
表4 e的取值为0和0.06时APTANE发现的FDs对比 Tab. 4 Comparison of FDs found by APTANE when e is 0 and 0.06
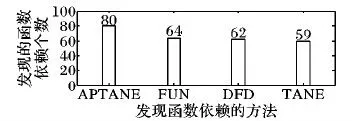
图5 高校数据集上各算法发现出的FDs个数Fig. 5 Number of FDs found by each algorithm in university dataset
经过在该真实数据集上进行缺失值填补的实验后发现,在使用AP聚类算法对缺失值进行填补之后,从数据集中发现的满足非平凡、最小要求的有效函数依赖个数增加到了80个,相对于直接在原始数据集上使用TANE、DFD、FUN算法来发现函数依赖的结果来看,分别增长了35.6%、29.0%、20%。表5展示了发现的部分有效FDs,在使用AP聚类算法填补缺失值之后,发现的有效函数依赖完全覆盖了之前存在缺失值时所发现的函数依赖。

表5 高校数据集部分有效函数依赖 Tab. 5 Partial effective functional dependencies of university dataset
从表5中可以看出:相比于数据集存在缺失值时发现出的函数依赖集合而言,使用AP聚类算法填补缺失值之后,除了在含有缺失值时发现的诸如:学号→困难程度,身份证号码→出生日期这些函数依赖之外,新增的函数依赖中包括了人均年收入→困难程度,困难等级、人均年收入→困难程度等函数依赖,这些FDs可以在后续的数据治理过程中,作为根据学生对应的家庭人均年收入来判断困难程度是否正确的检测规则。可以看到含有缺失值对于从数据集中准确发现有效的FDs影响较大,并且发现的函数依赖可能不准确,如果使用含义错误的函数依赖对高校数据进行数据治理,将可能在数据集中产生更多的脏数据。
本文实验在测试数据集和真实数据集上的结果表明了使用AP聚类算法来填补缺失值是有效且准确的,并且在填补缺失值后的数据集上发现的函数依赖的个数更多,含义更准确,能有效减少领域专家的工作量,提升高校数据的数据质量。
4 结语
为了解决在高校数据集存在缺失值时,发现的函数依赖个数较少且不准确的问题,本文提出了一种使用AP聚类算法和TANE算法相结合的APTANE方法。经过该方法的处理可以有效地补全缺失信息,提高发现的函数依赖的个数和准确度,为学校领导、老师从数据中分析学生行为、制定发展方略提供数据支撑,并且本文也证明了AP聚类算法在对缺失值进行填补方面是有效且稳定的。
但本文研究也存在不足之处,由于AP聚类算法的时间复杂度为O(N*N*logN),N为数据集的元组数,因此,在使用AP聚类算法对数据量较大的数据集进行缺失值填补时,算法耗时较长,并且发现的函数依赖所表达的字段间的含义并非都是准确的,因此,今后的研究将着眼于:1)如何在使用AP聚类算法保证缺失值填补准确率的同时减少算法运行时间;2)如何进一步提升发现的函数依赖所表达的字段间关联关系的准确度。

