考虑机床折旧的柔性作业车间绿色调度算法
王建华,潘宇杰,孙 瑞
(江苏大学 管理学院,江苏 镇江 212013)
0 引言
环境污染是近年来我国重点关注的热点问题。据有效数据不完全统计,中国工业能源消耗占社会总能源消耗的70%,而二氧化碳排放量占总二氧化碳排放量的83.1%,可以看出,大部分的能源消耗以及二氧化碳排放都来自于工业行业[1],因此能源的使用效率成为了工业企业关注的重点。
绿色制造正是在这一背景下逐渐成为企业界与学术界的常议话题之一[2]。绿色制造作为现代先进制造模式,其主旨为在不降低产品功能与质量的前提下,尽可能地降低生产成本,同时兼顾环境污染与能源浪费问题,进而实现经济指标和绿色指标多目标的协同优化[3],而绿色车间调度作为绿色制造的重要一环,近年来也成为了学术界研究的热点。虽然绿色车间调度已经引起了学者们的关注,但是相关的研究文献还较少。李玉霞等[4]基于设备选择和作业顺序规划提出了一种二阶低碳调度模型用于解决车间调度问题;Adekola等[5]和Capón-García等[6]分别研究了丙烯酸纤维生产的批处理问题,用于解决以经济指标和绿色指标为目标的多目标车间调度问题;Ding等[7]针对作业车间调度问题以产品总完工时间不超过截止时间为约束,优化生产过程的总电耗。
上述文献的研究对象大都是传统车间调度问题(Job-shop Scheduling Problem, JSP),所研究的内容较为简单,而关于柔性作业车间调度问题(Flexible Job-shop Scheduling Problem, FJSP)的绿色车间调度研究还相对较少。柔性作业车间区别于传统作业车间,具有工序顺序、工艺路线和机器的不确定性。朱伟[8]提出一种改进非支配排序遗传算法解决柔性作业车间多目标调度问题;Gong等[9]设计了一种模因算法用于解决具有工人柔性的多目标柔性车间调度;Zheng等[10]提出一种基于知识导向的果蝇优化算法求解具有双资源约束的柔性作业车间调度问题。上述研究中,多是只从经济目标角度出发解决柔性作业车间问题,少有考虑绿色目标,本文将从机床折旧的角度进行考虑,机床在使用过程中不可避免地产生折旧,从而导致单位时间内产生的能耗增加,使用时间越久的机床,单位时间内产生的能耗越多。因而在作业调度过程中,若有若干个调度方案完工时间相同,但因使用的机器不同导致产生的能耗不同,进而可以选择能耗低的方案,此类方案大多使用折旧低的机床。
在求解方法方面,现有的研究提出了许多改进遗传算法用于解决流水车间问题以及作业车间问题[11-13],但是并未考虑引入均衡分散原则用于生成初始种群,因此本文建立了以最大完工时间和总能耗加权和最小为调度目标的柔性作业车间绿色调度模型,同时设计了一种改进的遗传算法(Improved Genetic Algorithm, IGA)对其进行求解。在IGA中,不仅采用了一种三维实数的编码方式、便于动态变化的工序机器号选择与加工时间的数据存储;同时提出了结合均衡分散原则的初始种群产生方法,使遗传算法的收敛速度和全局搜索性能显著提升,降低陷入局部最优解的概率,使初始种群的解均匀遍布整个解空间。最后结合Brandimarte算例验证所提出的算法的可行性和有效性,同时也分析了不同权重比例对最大完工时间和总能耗的影响。
1 柔性作业车间绿色调度问题
1.1 问题描述
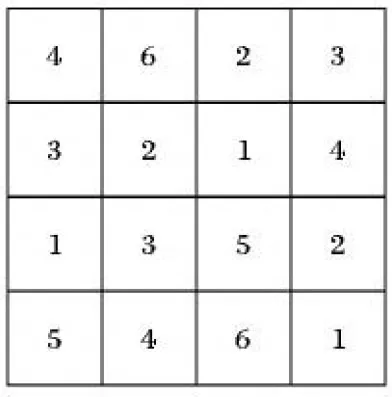
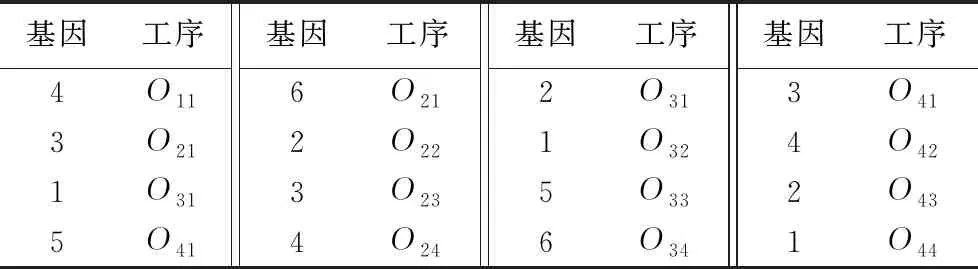
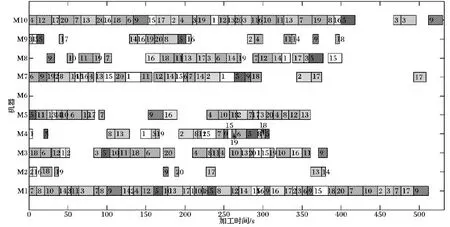
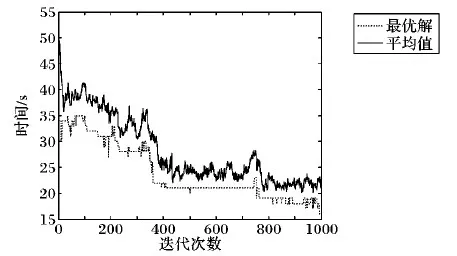
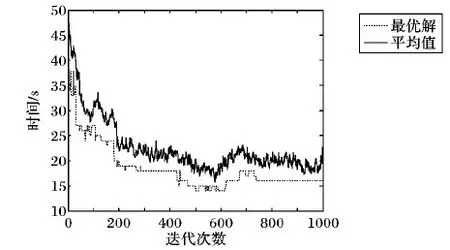
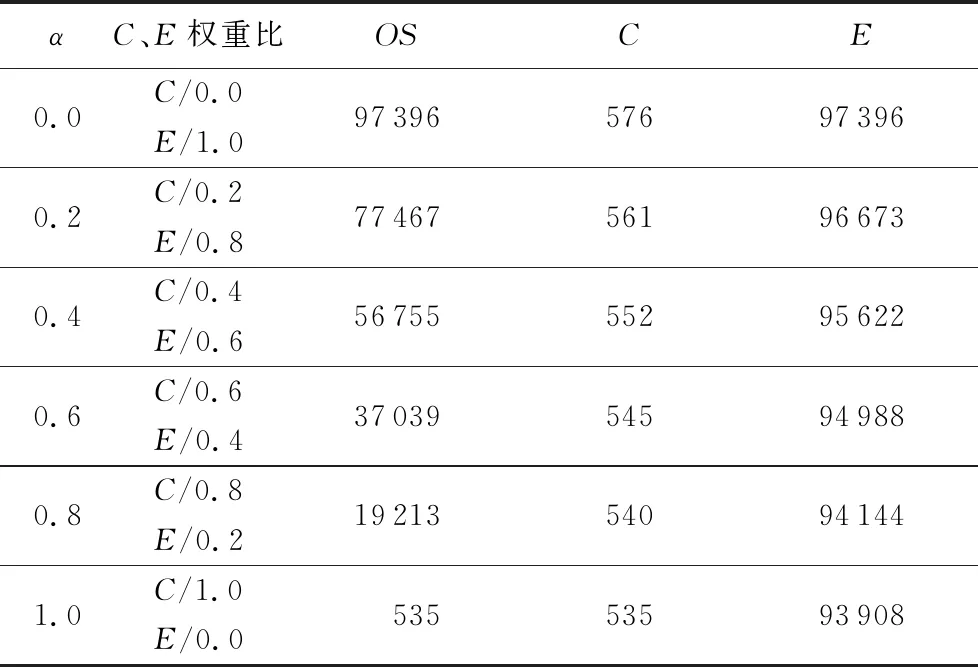
对于柔性作业车间绿色调度问题可以有如下描述:车间中有n个工件在m台机器上加工,工件i(i=1,2,…,n)具有Ni道工序,其中不同工件的工序数量可以不等,在本文中不考虑工件的工序顺序柔性,因此每个工件只有一条指定的工艺路线;工件i的第j道工序Oij具有一定可选择的机器数mij(mij 表1 简单FJSP模型 Tab. 1 Simple FJSP model 在对本文提出的问题建立模型之前,首先对问题作一些合理的假设,以保证研究结果的严谨性和准确性:1)工序不能在加工过程中被打断;2)本文不考虑工件在加工前的准备时间以及加工过程中的搬运时间;3)机器不会在加工过程中出现故障;4)每道工序仅能被一台机器上加工一次;5)每台机器在每个时刻只能加工一个工件;6)同一工件的不同工序必须在不同的时刻被加工;7)在初始时间,机器处于停止运转状态,且机器上没有代加工工件;8)在初始时间,所有工件的原材料准备完毕;9)机器一旦开启,只有加工完该机器所需加工的最后一道工序才停止运行,其余时间保持空载状态。 1.2.1 符号定义 为方便讨论及读者对本文的理解,现对本文中出现的所有符号作定义,如表2所示。 表2 符号定义 Tab. 2 Symbol definition 1.2.2 模型建立 基于以上问题描述以及条件假设,结合本文的调度目标为最大完成时间和总碳排放量的加权和,其中总能耗的计算公式参照文献[14]所提出的普通机械加工设备工步间空载运行时停机节能的理论决策模型。其能耗分布如图1所示,其中:t0~t1为机器的启动时间,t2~t3,t4~t5都是机器的加工时间,t1~t2及t3~t4为机器的空载时间,t5~t6为机器的停机时间。 图1 机床加工功率变化Fig. 1 Machine tool power change 结合本文研究问题以及上述表2的参数设定,可以得到机器在启动、负载、空转、停止时各产生的能耗。 (1) (2) (3) (4) 进而可以得到在整个生产过程中总的能量消耗: E=Eb+Ec+El+Ef (5) 其中:式(1)表示机器启动的总能耗;式(2)表示机器负载时的总能耗;式(3)表示机器空转时的总能耗;式(4)表示机器停止运转的总能耗;式(5)表示所有机器的总能耗。 时间是企业生产时考虑的最重要的因素,同样能耗也是一项重要指标,本文的目标函数是使最大完工时间(Makespan)CT和总能耗E的加权和最小,以此建立如下FJSP模型。 (6) s.t.Cij-Sij=Pij;i=1,2,…,n,j=1,2,…,Ni (7) Mij∈mij (8) (i,k)=1,2,…,n,(j,v)=1,2,…,Ni (9) Sij≥Ci(j-1);i=1,2,…n,j=1,2,…,Ni (10) m=1,2,…,k (11) Xkvij∈{0,1},(i,k)=1,2,…,n, (j,v)=1,2,…,Ni (12) Kijm∈{0,1};i=1,2,…,n, j=1,2,…,Ni,m=1,2,…,k (13) 其中:式(6)表示目标函数,OS为所求的目标值,代表最小的最大完工时间C和总能耗E的加权和;式(7)表示工序不能在加工过程中被打断;式(8)表示每道工序有且仅能在一台机器上进行加工,并且只能加工一次;式(9)表示每台机器一次在每个时刻只能加工一个工件;式(10)表示同一个工件的不同工序需要在不同时间被加工,且时间不能有重叠;式(11)表示机器一旦开启,需要在加工完该机器上的最后一道工序才停止;式(12)表示0- 1变量,若工序Oij在工序Okv之后加工,则Xkvij=1,否则Xkvij=0;式(13)表示0- 1变量,若工序Oij在机器m上加工,则Kijm=1,否则Kijm=0。 本文所求解的绿色FJSP问题主要有两个子问题,即每道工序机器的选择以及工序在机器上的加工顺序,FJSP已被证实属于NP-hard问题,而对于大规模的FJSP更是属于求解困难的问题。针对这些问题设计了一种改进遗传算法用于求解绿色FJSP。遗传算法是一种具有随机、自适应和高度并行特点的优化算法,由Holland教授于1975年首次提出,但也存在着明显的缺点,遗传算法的本质是随机性的搜索,不能保证最终所得解为全局最优解[15-16]。针对这一问题,本文引入正交实验的均衡分散原则生成初始种群,保证初始种群分布于用于整个解空间,提高初始种群的质量;同时采用三维实数的编码方式,避免了交叉操作后重复基因片段的产生,具体操作步骤如下: 步骤1 设置参数:种群规模N、迭代次数count、交叉概率Pc以及变异概率Pm。 步骤2 产生初始种群。令i=0,结合均衡分散原则随机产生初始种群P。 步骤3 计算种群的适应度值。采用权重分配法为两个目标分配权重,然后求和得到个体适应度值。 步骤4 判断终止条件,如果满足条件(i>count),则输出最优解;否则进行下一步。 步骤5 进行选择操作,采用轮盘赌的方法选择适应度值较优的个体进入新的种群,种群规模仍为N。 步骤6 进行交叉操作,从种群中选取两个个体,若random>Pc,则用双个体算术交叉的方式对其进行交叉操作,然后放入新的种群;否则将两个个体直接放入新的种群,直到所有的个体都执行了交叉操作为止。 步骤7 进行变异操作,根据变异概率Pm判断是否对个体进行变异操作,若random>Pm,则用动态步长的方式对其基因片段进行变异;否则进行下一步操作。 步骤8 求出当前种群的最优解,令i=i+1,返回步骤4。 本文采用三维实数的编码方式[17],用元胞结构进行存储,存储结构为N×n×Ni,这种编码方式的好处是方便对其中的基因进行修改以及交叉时不会产生冲突基因。每道工序的机器号为一条染色体的基因,每个染色体拥有n×Ni个基因,而一个种群拥有N条这样的染色体。例如图2所示为4×4的一条染色体,行代表同一个工件的不同工序的机器号,列代表不同工件的同一道工序的机器号,0表示该工件的该工序不存在。 图2 染色体示例图Fig. 2 Example diagram of chromosome 染色体中基因的位置决定了工件的加工顺序,先自上而下加工所有工件的第一道工序,再同样加工所有工件的第二道工序,直至所有工序都加工完成,例如图2染色体对应的加工顺序转化为表3,首先加工O11,再加工O21,然后继续加工其余工序。 表3 基因加工顺序 Tab. 3 Gene processing sequence 初始种群解质量与最优解之间的差距很大程度上决定了GA的搜索性能,而一般采用随机方式产生的初始种群很难保证解的质量,在搜索过程中难免会造成陷入局部最优解以及增加搜索时长的情况。为了加强GA的全局搜索性能,本文结合均衡分散原则来生成初始种群,均衡分散原则是实验设计(Design of Experiment, DOE)中的常用方法[18],在实验安排中,所挑选出来的水平组合是均匀分布在所有水平空间的,均衡分散原则如表4所示。以此原则为基准的初始种群生成方法主要遵守三个原则:1)所有机器被选择的次数相等;2)同一工件的不同工序选用不同机器;3)不同工件的同一工序选用不同机器。以此方法生成的每一个解都具备三个维度上的分散性,提升了解的质量,具体步骤如下: 步骤1 建立调用机器次数初始集a1×k=[0,0,…,0]。 步骤2 随机生成工序Oij的机器号Mij,令am=Mij,其中Mij∈mij,m代表机器号。 表4 均匀分布点数 Tab. 4 Evenly distributed points 假设存在一个每个面都有9个点的立方体中,根据均匀分散原则,在所有的面上都需要均匀分布点数,如表4所示坐标,在立方体中均匀分布着9个点。具体示例如图2所示,该表为4×4的一条染色体,共有4个工件,每个工件4道工序,最终所选的机器集体现了上述三个原则,但考虑到实际情况中机器平均调用次数不一定为整数,本实例中共有6台机器,每台机器的理想调用次数为2.6,而机器1~4都调用三次,机器5、6调用两次,因此原则1)可以具有一定柔性。 选择操作的目的是为了让具有高适应度值的染色体存活下来,而高适应度值意味着该个体的解质量更高,在一次次迭代过程中,种群的规模N是固定不变的,但是其中的染色体是在不断变化的,并且是朝着好的一面发展。本文采用轮盘赌的方法选择染色体个体,具体步骤如下: 步骤2 随机产生α,α∈(0,1),若α∈(∑fi′,∑fi+1′),则选取第i个个体,将此步骤循环N次,即得到新的种群。 在IGA中,交叉操作选择双个体算术交叉的方式,在基于机器的编码或基于工件的编码方式中,通常在两个被选中染色体的相同位置选取两个或者多个交叉位进行交叉,随后再进行冲突检测,检查重复的基因片段,而在本文所采用的三维实数的编码方式中,需要将该交叉方式进行改进,同时避免了产生相同的基因片段,无需进行冲突检测,减少了交叉操作的步骤,示例如图3所示,具体步骤如下: 步骤1 随机从种群N中选取两条染色体,染色体结构为n×Ni,随机确定两个数βi,βj,β=(β1,β2,…,βn),其中βi∈{1,2,…,Ni},N=N-2。 步骤2 在两条染色体的每一行都确定一个交叉位,每个交叉位置的选择用β,然后将两条染色体进行交叉。继续步骤1的操作,直至N=0。 图3 染色体交叉Fig. 3 Chromosome crossover 变异操作的目的是为了保证种群的多样性,同样也是为了增加算法的搜索方向,防止遗漏某些区域的解。本文因采用的是实数编码,所以选择动态步长[16]的方式来进行变异操作,从而达到搜索该方向局部空间的效果,实例如图4所示,具体步骤如下: 步骤1 随机生成X=(ε1,ε2)用于确定需要执行变异操作的基因,其中ε1∈{1,2,…,n},ε2∈{1,2,…,Ni},X为选中的机器号。 步骤2 确定基因的搜索方向,若X≤k/2,则搜索方向为正方向{X+1,X+2,…,k};否则搜索方向为负方向{1,2,…,X-1},其中X∈{1,2,…,k}。 步骤3 确定搜索的步长。为了保证局部搜索的有效性,若搜索方向为正方向,则将步长确定为L1,若L1不存在,将步长变为L3,直至步长存在L2i+1;否则步长为L2,L2不存在变为L4,直至步长存在L2i,其中L=(X+1,X-1,X+2,X-2,…,k,1)。 图4 染色体变异实例Fig. 4 Example of chromosomal variation 为了验证IGA的有效性,本文采用Matlab 2014a的M语言进行编程,并在Windows 7,Intel Core i5- 3337U,CPU 1.8 GHz,内存4 GB,64位操作系统的计算机上运行。在整个实验过程中,IGA的参数设置如下:迭代次数count=1 000,种群规模N=200,交叉概率Pc=0.8,变异概率Pm=0.1。 3.1.1 实验1(8×8问题) 实验1的8×8工件测试数据来自于文献[19],由8个工件、8台机器组成,为了测试IGA的性能,将其目标函数设定为最小化最大完成时间,将所得结果与SPT规则、传统GA以及Zhang等[20]提出的GA测试结果进行对比,其中SPT所能求得的最优解为19,传统GA求解的最优解为16,Zhang等[20]的方法求得的最优解为14,而本文所提算法求得的最优解为14,由对比数据可知,IGA的求解结果已达到文献记录中的最优解,图5显示了8×8算例中Makespan为14的调度方案。 3.1.2 实验2(基准Brandimarte算例) 为了更好地验证IGA的有效性,在基准Brandimarte算例MK01~MK08的基础上分别运行10次,并取其中的最优解分别与田旻等[21]提出的分层混合遗传算法(Hierarchical Hybrid Genetic Algorithm, HHGA),Ziaee[22]提出的基于构造过程的启发式算法(Heuristic Algorithm Construction Process, HACP),夏俊红等[23]提出的改进萤火虫(Improved Glowworm Swarm Optimization, IGSO)算法进行对比。 从表5的统计结果来看,MK02、MK03以及MK06已经达到了相关文献算法的最优值,其余问题的结果也接近于相关文献算法的最优值。与单个算法相比,本文算法得到的结果有7个优于HACP得到的结果,有3个优于HHGA得到的结果,有7个接近或等于IGSO得到的结果,由此可见本文算法与其余三种算法相比具有一定的优越性,图6显示了20×10算例中最大完成时间为530的调度方案。 图5 8×8实例(Makespan=14)调度方案Fig. 5 Scheduling scheme of 8×8 instance (Makespan=14) 图6 20×10实例(Makespan=530)调度方案Fig. 6 Scheduling scheme of 20×10 instance (Makespan=530) 表5 Brandimarte算例结果分析 Tab. 5 Analysis of Brandimarte example results 3.1.3 算法分析 图7为实验1中传统GA的收敛曲线,图8为IGA的收敛曲线,从图7~8中可以看出,传统GA在第1 000代的时候才得到了最优解,而IGA在420代的时候已经得到了传统GA最优解相等的值,并在大约500代的时候得到了IGA所能得到的最优解。此外,IGA在开始阶段就快速收敛,并在之后收敛速度减缓,说明了IGA初始解集的质量较高,具有一定的全局搜索性能。 图7 8×8实例传统GA收敛曲线Fig. 7 Traditional GA convergence curve of 8×8 instance 图8 8×8实例IGA收敛曲线Fig. 8 IGA convergence curve of 8×8 instance 对于以最大完工时间(Makespan)CT和总能耗E的加权和最小为目标函数的绿色FJSP,为了保证实验结果的可信度,数据采用基准Brandimarte算例的MK08,因其最终的Makespan较大,能够较为明显比较出不同α值得到结果的差异。机器的四阶段(开机、空载、加工、关机)单位能耗取[42,14,25,43][24],同时考虑新旧机器单位能耗不同的因素[25],因不同使用年限的机器能耗不同,在这里本文假设旧机器的单位能耗为新机器的1.2倍,MK08算例中的10台机器M1~M5为新机器,M6~M10为旧机器,因此旧机器的四阶段(开机、空载、加工、关机)单位能耗为[50,17,30,52]对于α分别取[0.0,0.2,0.4,0.6,0.8,1.0]六个维度,测试结果如表6所示。 表6 不同α取值的绿色FJSP结果 Tab. 6 Green FJSP results with different α values 为了更好地分析不同α取值对OS、C、E的影响,将OS与E分别取除以100得到对比结果,如图9所示。 图9 FJSP结果分析Fig. 9 Analysis chart of FJSP results 从图9可以发现:在α不断增大的过程中,最大完成时间逐渐缩小,而总能耗也呈逐渐下降的趋势,因此可以得出结论,最大完成时间与能耗呈正相关关系,企业在追求完工时间最小化的同时,也在潜在地追求能耗的最小。 针对绿色FJSP进行研究,本文设计了IGA用于解决该类问题。依据GA的缺陷,采用三维实数的编码方式,并在初始解集生成阶段引入均衡分散原则,确保初始解集均匀分散在整个解空间,保证了初始解集的质量;在交叉阶段选用双个体算术交叉的方式,结合实数编码方式能够避免单个解内部的冲突;在变异阶段采用了动态步长的方式进行变异,保证了对局部空间的有效搜索。最后将IGA运用于两个实验,实验结果表明了IGA求解FJSP的有效性,同时分析了不同权重比例对最大完工时间CT和总能耗E的加权和的影响,实验结果表明最大完工时间与总能耗呈正相关关系。 本文的不足之处在于仅考虑了机器柔性,下一步的研究方向是考虑其他的柔性约束,此外对于大规模调度,库存对于工件的加工顺序影响也值得研究。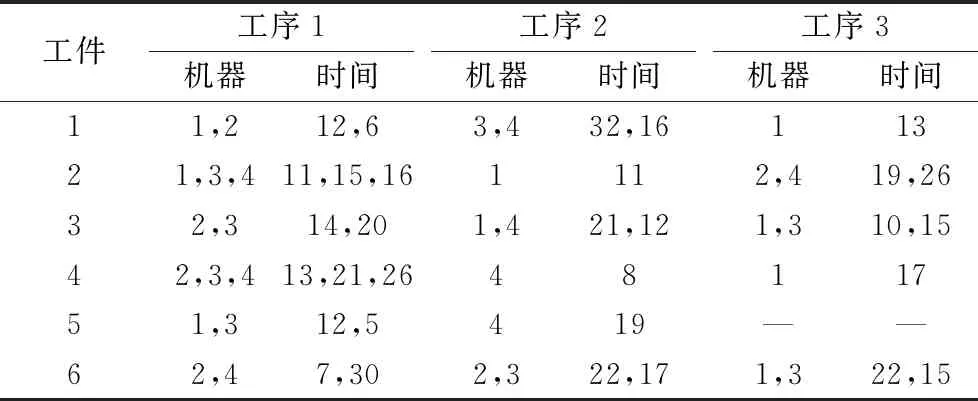
1.2 柔性作业车间绿色调度问题模型建立



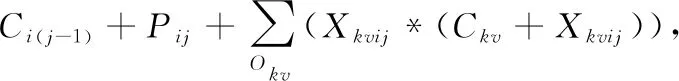
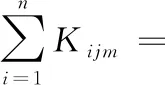
2 改进遗传算法设计
2.1 编码机制
2.2 初始种群的产生
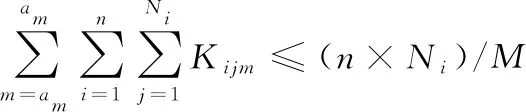

2.3 选择算子
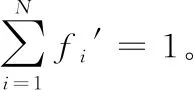
2.4 交叉算子

2.5 变异算子

3 算例研究和结果分析
3.1 IGA性能分析

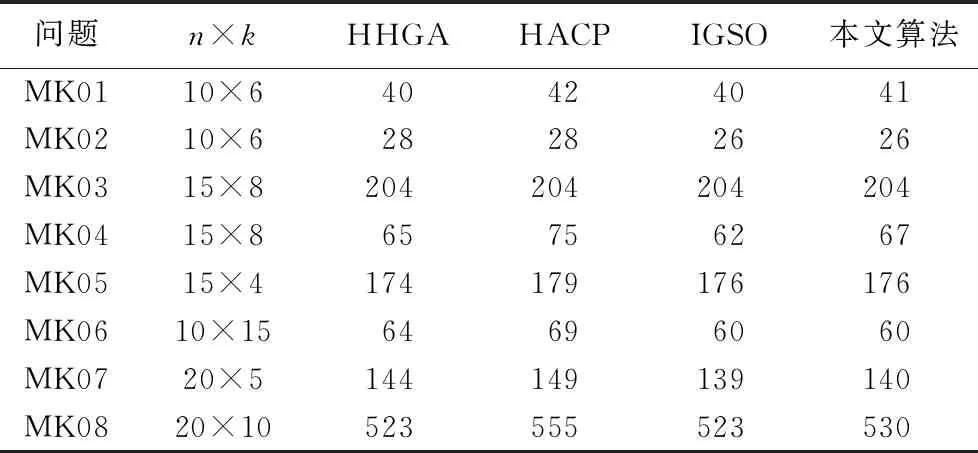
3.2 绿色FJSP结果分析

4 结语

