基于声固耦合的水下复杂目标声散射研究

周 烨, 温 玮, 韩建辉, 杨日杰

基于声固耦合的水下复杂目标声散射研究

周 烨, 温 玮, 韩建辉, 杨日杰

(海军航空大学 战勤学院, 山东 烟台, 264001)

针对现有简单模型对水下实际目标的仿真逼真度较差的情况, 利用COMSOL声固耦合算法以及完全匹配层对二维潜艇简单模型受激励后的散射声场进行了数值仿真分析。利用ANSYS有限元分析软件对相同简化模型进行计算对比, 计算结果基本吻合, 验证了COMSOL在计算大型目标散射声场时的有效性。最后以某型潜艇结构为原型构建了内部舱室结构及结构材料属性, 提高了模型相对于实际目标的逼真度, 仿真了受激励后的再辐射声场。其结果可对水下主动探测装备发展提供参考。

潜艇; 散射声场; 声固耦合; 完全匹配层

0 引言

水下目标声散射可看作目标受激励后的再辐射过程。随着电子计算机技术的不断发展, 有条件对水下目标散射声场进而对主动声呐回波信号进行较为精确的数值仿真, 避免了频繁进行海试试验, 节省了大量的人力物力[1]。通过相关文献发现, 国内对于水下结构的散射声场数值仿真大都采用有限元与边界元相结合的方法, 并在工程应用方面取得了良好的结果[2], 但只是针对简单模型进行仿真。近年来, 有学者利用新型多物理场耦合分析软件COMSOL Multiphysics进行了简单形状模型以及小型加肋壳体模型的尝试[3]。初步验证了利用该软件计算目标散射声场的可行性, 但未见更复杂模型的仿真报道。而更加真实的目标结构建模在仿真应用中又是不可忽略的, 因此文中借助COMSOL软件对复杂潜艇舱室结构进行了声固耦合数值仿真分析, 为提高主动声呐回波信号仿真逼真度提供了有效借鉴。

1 理论研究

1.1 声场有限元结构

对于模拟无限场条件下的数值计算, 一般需要构造一个有限的求解域[4], 通过对求解域内进行有限剖分, 建立结构体和流体的有限元方程求解[5], 并且对结构连接处进行部分网络细化, 如图1所示。由于声波主要在流体中进行传播, 可以将流体看作特殊的声学介质, 将其离散化, 在只考虑体积应变相关力的同时忽略剪切应力[6]。但是因流体粘性等原因导致的速度耗散无法忽略, 并且其介质属性可以给出相应的阻抗或者反射边界条件[7]。对于可压缩的绝热流体环境, 可以给出运动方程[8]

图1 简单潜艇模型网络剖分及精细化结构处理

假设流动是非定常的, 不考虑对流带来的影响。对于无粘性、线性和可压缩流体, 声压值和体积模量与应变有关, 可以表示为

式中:为体积模量; 剩余项表示体积应变。

1.2 声固耦合

将流体结构看成弹性体介质。在流固界面上会产生流体负载, 同时声压也对结构体产生弹性应力[10]。结合流体波动方程和结构动力方程可以计算弹性结构表面的位移和声压。对于波动方程

应用其变分形式

又因为声场内声压满足入射声场和散射声场的叠加, 故有

将其代入式(4), 可得

对于各向同性的均匀线弹性体, 其结构方程可以写成

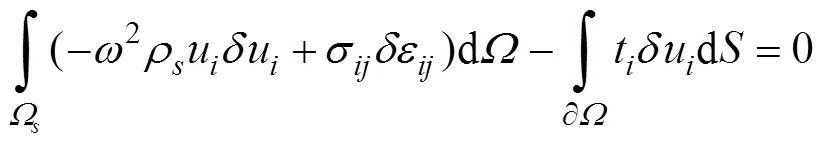
2 模型仿真

2.1 简单潜艇目标模型

为了在无限水域中建立有限元模型, 需要阻绝模型边界反射对于目标声场的影响。这里引入Berenger提出的完全匹配层(perfectly matched layer, PML), 其主要是在目标周围构造起一个封闭空间, 散射声波到达PML时, 会迅速衰减吸收, 构造出一个无反射边界, 从而不会影响空间内的散射声场[10-11]。为精确计算结果, 整个模型采用自由三角形网络进行剖分, 如图1所示。建立潜艇模型长度为50 m, 直径8 m, 指挥台高度2 m, 长5 m, 外围包裹厚度为2 m的PML。模型材料设定弹性模量为203 GPa, 泊松比为0.29, 密度为7 880 kg/m3, 流体声速设定为1 500 m/s, 密度为1 000 kg/m3, 设定平面波沿轴正半轴入射。在进行网络剖分时, 为了达到较为精确的结果, 空间步距应该小于辐射波长的1/6。

2.2 有效性验证

利用COMSOL可进行简单形状的水下目标数值分析, 已经有人通过对比解析解以及实验验证了其有效性[12-13], 但是对于大型复杂形状的水下目标数值仿真是否仍然保持准确并没有相关介绍。由于ANSYS在计算水下复杂目标声散射方面已被业界广泛接受, 为了验证COMSOL在计算大型潜艇目标时的有效性, 使用ANSYS分析软件建立相同模型进行仿真计算, 并将结果进行对比。图2显示了在距离潜艇艇艏10 m和200 m处的散射声压级仿真结果。

由图2可以看出, 2种计算方法在大型目标模型计算上有很好的一致性, 反映了COMSOL在分析大型潜艇模型声散射方面具有可行性。同时, 由于自身具有强大的后处理功能, 针对三维目标其可以直接生成三维辐射方向图, 如图3所示。

通过对比仿真相同多物理场耦合模型时ANSYS软件和COMSOL软件的计算时间可发现, 随着仿真模型单元格数量的增加, COMSOL表现出在计算多物理场耦合高效性, 如图4所示。

图2 距离潜艇艇艏10 m和200 m处的散射声压级仿真结果

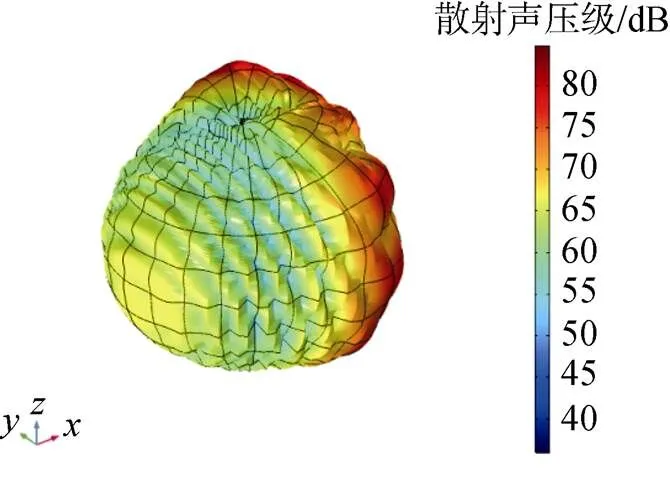
图3 500Hz平面波激励下的辐射方向图

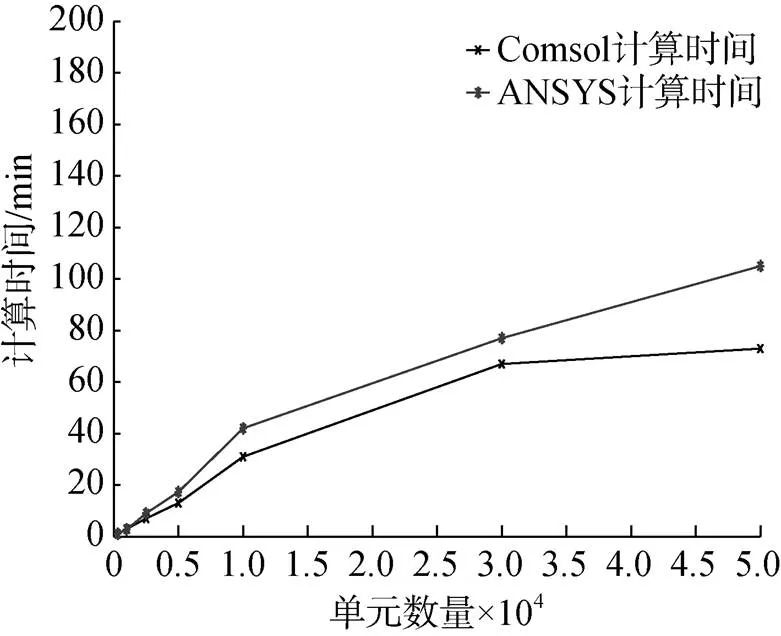
图4 计算效率对比

2.3 复杂水下潜艇结构仿真

为了更加真实地模拟潜艇散射声场特征, 需要考虑其内部舱室构造所带来的影响。文献[5]运用二维模型处理水下结构的仿真问题, 设计了针对轴对称目标的二维有限元数值计算方法, 证实了利用COMSOL所建立二维目标散射模型同样可以反映真实的水下声场环境, 同时节省了大量的计算时间, 使得建立复杂精细的舱室结构模型仿真得以实现。如图5所示, 在COMSOL中依据某型双壳潜艇构造建立二维仿真模型, 在内壳与外壳处建立肋状结构模拟支撑板。

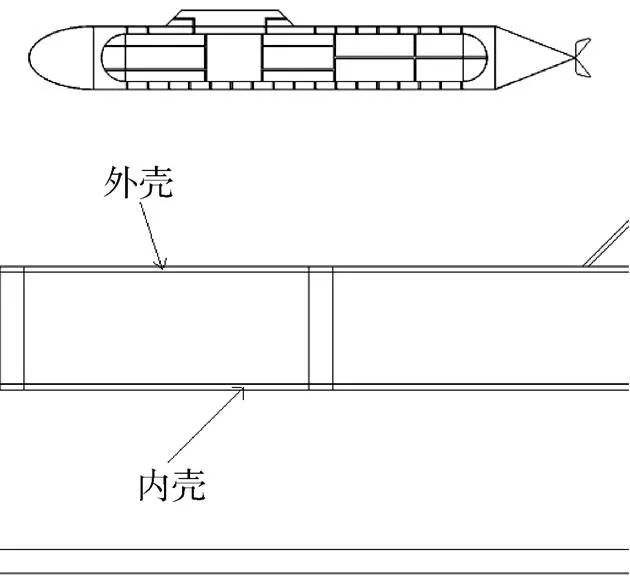
图5 潜艇舱室结构建模及内部支撑结构

如图6所示, 设定潜艇目标在水下150 m处类比三维模型, 在水体四周设立完美匹配层来模拟无限场。建立潜艇模型长度50 m, 指挥台高度2 m, 长5 m, 外围包裹厚度为1 m的PLM层。潜艇外壳设定为钢铁材质, 模型材料设定弹性模量为203 GPa, 泊松比为0.29, 密度为7 880 kg/m3, 声速为5 880 m/s。内壳设定为钛合金材质, 设定弹性模量为117 GPa, 密度为4 500 kg/m3, 泊松比为0.35, 声速为6 100 m/s。设置典型声速剖面, 如图7所示, 横坐标为深度, 纵坐标为水中声速, 与简单模型背景声场相同, 采用一系列特定频率平面波以0°入射, 计算模型受激励后的响应。

图6 水体环境建模

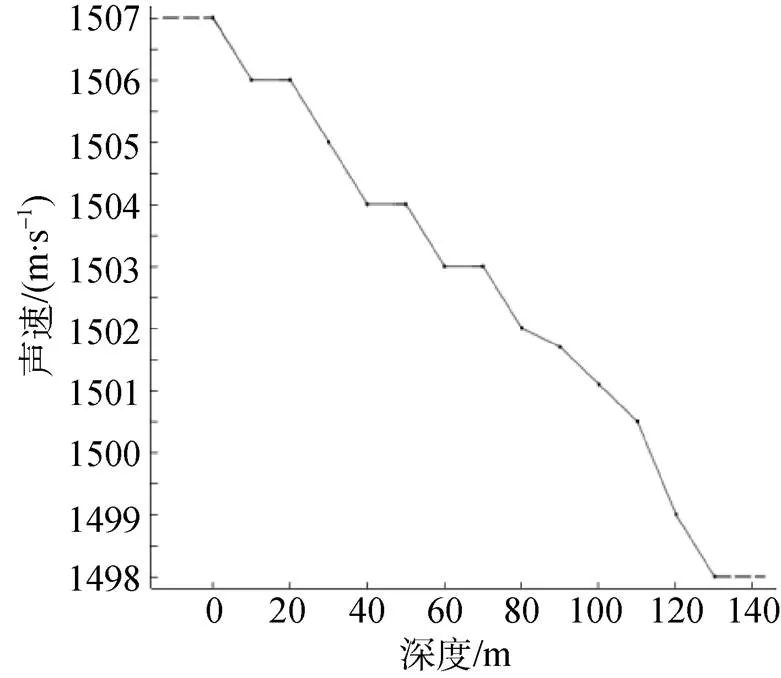
图7 声速剖面

通过仿真计算, 得出距离舰桥上方50 m处的单壳体模型与舱室结构模型的散射声压级曲线, 分别如图8和图9所示。

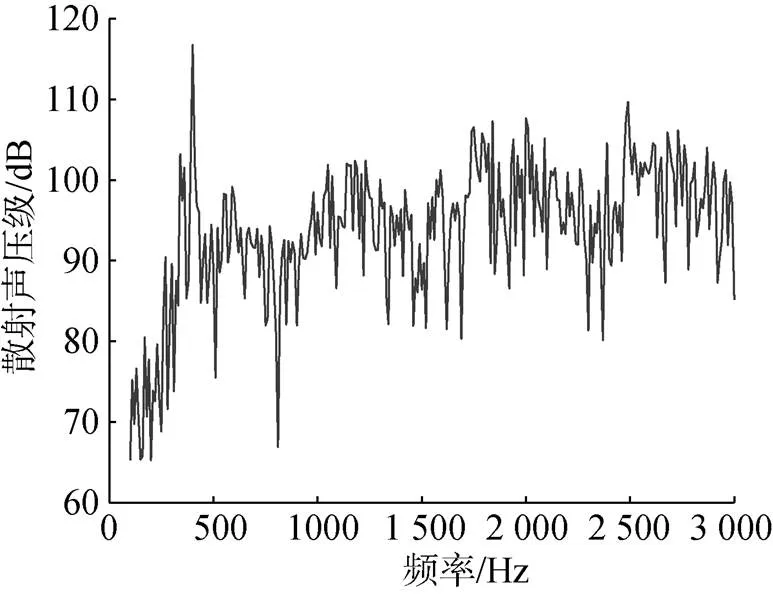
图8 单壳体模型散射声压级曲线

图9 结构模型散射声压级曲线

由图8和图9可以发现, 2种模型在数值上大致接近, 但是精细化的舱室结构散射曲线明显比单壳体模型要平滑很多, 这说明横梁以及支撑板组成的结构对于潜艇表面振动产生了明显的抑制作用。由于计算结果代表了模型在一组特定频率下的散射声压级, 结果表明两者均在低频处产生了比较高的峰值, 且考虑舱室结构后其对于低频信号激励后的响应更加剧烈, 结构之间的相互影响加大。下面考虑声波在不同垂直方向角度的入射情况, 仿真在0°和45°入射平面波时, 其距离艇艏前10 m处的散射声压级曲线如图10和图11所示。由图可知, 仿真后的不同垂直方向角的改变对于模型声散射的影响在于低频响应的微弱改变, 对于散射声压级曲线的大体趋势影响不大。

图10 45°入射散射曲线

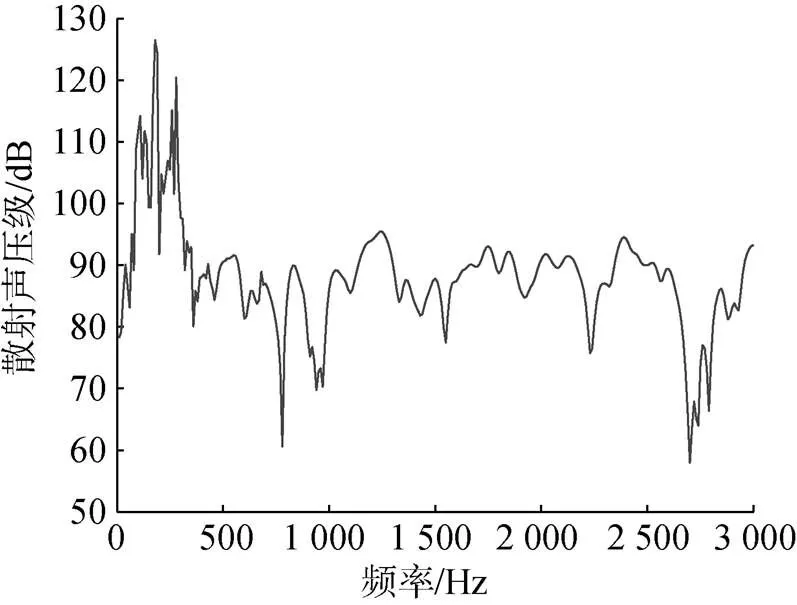
图11 0°入射散射曲线

接下来考虑正横方向入射时目标的散射声场情况, 建立潜艇纵切面模型, 如图12所示。

所建立模型直径8 m, 外壳以及支撑杆为不锈钢耐压壳, 厚度为1 m, 内壳为钛合金材料, 材料属性同上文。对比水平方向角0°与90°的声散射仿真结果如图13所示。

由图13可以发现, 在以90°水平角入射时, 也就是在正横方向, 对更多低频的信号响应明显, 且散射声强加大, 结构之间相互影响力增加。

图12 潜艇横切面模型

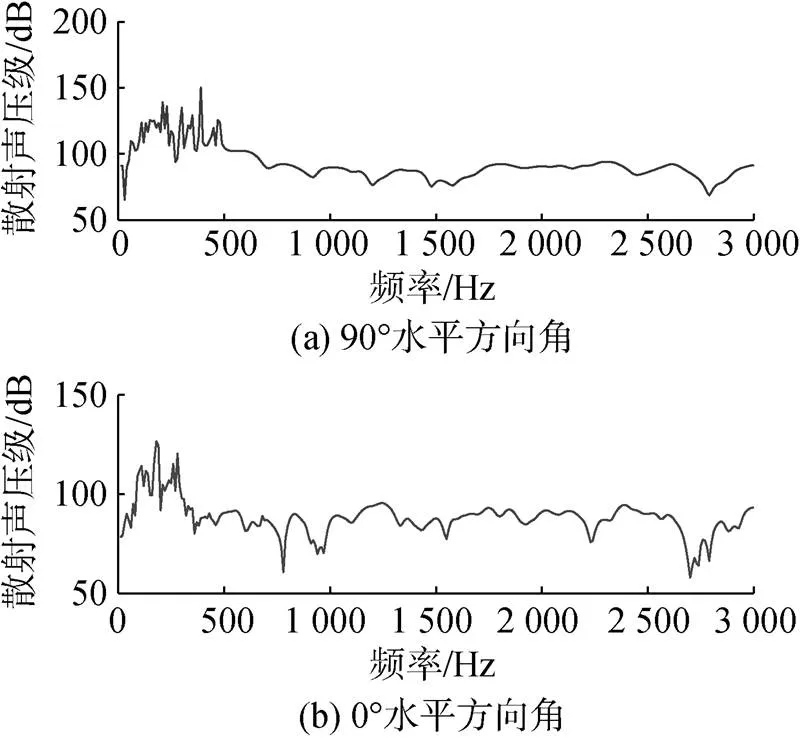
图13 水平方向角0°与90°的声散射仿真结果

3 结束语

文中通过ANSYS和COMSOL针对同一模型的仿真对比, 验证了COMSOL在复杂形状目标数值仿真方面仍能保持有效性。随后利用COM- SOL的PML以及多物理场耦合模块仿真了大尺度下的精细舱室结构潜艇模型, 并与单壳体潜艇模型进行对比, 说明了舱室结构相对于单壳体在受迫振动上有一定的抑制作用且对于低频激励响应比较强烈, 为主动探测设备发展以及潜艇消声提供了一定启示。当然, 文中建立的仿真模型包括设立的PML只是为仿真潜艇舱室结构下的近场声场环境。针对目标的远场声场可以利用COMSOL自带远场计算模块来计算自设条件下的远场声场, 如何在复杂环境参数包括环境噪声以及混响下仿真目标的远场回波情况将是下一步工作的重点。

[1] 孙乃葳, 李建辰, 万亚民, 等. 基于改进板块元法的潜艇目标强度预报仿真[J]. 鱼雷技术, 2016, 24(4): 254-259.Sun Nai-wei, Li Jian-chen, Wan Ya-min, et al. Simulation of Submarine Target Strength Forecast Based on Improved Planar Element Method[J]. Torpedo Technology, 2016, 24(4): 254-260.

[2] 于福建, 王斌, 张培珍. 起伏海底掩埋目标声散射特性数值仿真[J]. 水下无人系统学报, 2018, 26(6): 533-536.Yu Fu-jian, Wang Bin, Zhang Pei-zhen. Numerical Simulation on Acoustic Scattering Characteristics of Targets Buried in Fluctuating Seabed[J]. Journal of Unmanned Undersea Systems, 2018, 26(6): 533-536.

[3] 缪旭弘, 钱德进, 姚熊亮, 等. 基于ABAQUS声固耦合法的水下结构声辐射研究[J]. 船舶力学, 2009, 13(2): 319-324.Miao Xu-hong, Qian De-jin, Yao Xiong-liang, et al. Sound Radiation of Underwater Structure Based on Coupled Acoustic-structural Analysis with ABAQUS[J]. Journal of Ship Mechanics, 2009, 13(2): 319-324.

[4] Liu B, Niu W, Ruan X Z, et al. Observation of Small Polaron and Acoustic Phonon Coupling in Ultrathin La0.7Sr0.3MnO3/SrTiO3 Structures[J]. Physica Status Solidi(RRL)-Rapid Research Letters, 2019, 13(5): 1800657(1 of 6)-1800657(6 of 6).

[5] 张冠军, 朱翔, 李天匀, 等. 双层加筋板水下声振耦合特性研究[J]. 船舶力学, 2019, 23(1): 78-87.Zhang Guan-jun, Zhu Xiang, Li Tian-yun, et al. Vibro-acoustic Coupling Characteristics of Double Stiffened Plates Coupled with Water[J]. Journal of Ship Mechanics, 2019, 23(1): 78-87.

[6] 刘慧, 彭子龙, 范军, 等. 船坞登陆舰声散射时频特征数值及试验研究[J]. 声学技术, 2019, 38(2): 147-152.Liu Hui, Peng Zi-long, Fan Jun, et al. Numerical and Experimental Research on Acoustic Scattering Time-fre- quency Characteristics of Dock Landing Ship[J]. Tech nical Acoustics, 2019, 38(2): 147-152.

[7] 卢笛. 基于有限元原理的弹性目标声散射计算[D]. 哈尔滨: 哈尔滨工程大学, 2014.

[8] 钱治文. 浅海波导中弹性结构声辐射预报方法研究[D].哈尔滨: 哈尔滨工程大学, 2018.

[9] 张培珍, 李秀坤, 王斌, 等. 掩埋目标声散射特性及其实验[J]. 声学学报, 2018, 43(6): 934-942.Zhang Pei-zhen, Li Xiu-kun, Wang Bin, et al. Acoustic Scattering Experiments and Characteristics of Targets Buried in Sediment[J]. Acta Acustica, 2018, 43(6): 934-942.

[10] 刘学芳. 目标散射声场模拟及散射体尺寸的计算[D]. 西安: 陕西师范大学, 2017.

[11] 郭文杰. 含液面的多边界约束下潜浮圆柱壳声振模型研究及性能分析[D]. 武汉: 华中科技大学, 2018.

[12] 侯欣雨, 陈航. 水下无载波超宽带信号波形设计与回波特性[J]. 鱼雷技术, 2016, 24(5): 340-345.Hou Xin-yu, Chen Hang. Waveform Design and Echo Characteristic of Underwater Carrier-free Ultra-Wide Band Signal[J]. Torpedo Technology, 2016, 24(5): 340- 345.

[13] 石焕文, 盛美萍, 孙进才, 等. 加纵肋平底圆柱壳振动和声辐射的FEM/BEM研究[J]. 振动与冲击, 2006, 25(2): 88-92.Shi Huan-wen, Sheng Mei-ping, Sun Jing-cai, et al. On FEM/BEM for the Problems of Vibration and Acoustic Radiation from an Axially Stiffened Cylindrical Shell with Two End Plates[J]. Journal of Vibration and Shock, 2006, 25(2): 88-92.

Research on Acoustic Scattering of Underwater Complicated Target Based on Sound-Solid Coupling

ZHOU Ye1, WEN Wei1, HAN Jian-hui1, YANG Ri-jie1

( Air Combat Service College, Naval Aviation University, Yantai 264001, China)

In view of the low simulation fidelity of the existing simple model for actual underwater target, the scattered acoustic field of the two-dimensional simple model of submarine after excitation is simulated numerically by using the COMSOL sound-solid coupling algorithm and the perfectly matched layer(PML). The result is compared with that of the same model calculated by using the finite element analysis software ANSYS, and both results are basically consistent, verifying the effectiveness of the COMSOL sound-solid coupling algorithm in calculating the scattered acoustic field of large target. Furthermore, the interior cabin structure and its structural material attributes are established for a submarine structure, which improves the fidelity of the model to the actual target, and the sound field of re-radiation after excitation is simulated. The simulation results may be taken as a reference for the numerical analysis of active sonar signals and the development of underwater active detection equipment

submarine; scattered acoustic field; sound-solid coupling; perfectly matched layer(PML)

相关文章导航

1. 于福建, 王斌, 张培珍. 起伏海底掩埋目标声散射特性数值仿真[J]. 水下无人系统学报, 2018, 26(6).

2. 杨益新, 韩一娜, 赵瑞琴, 等. 海洋声学目标探测技术研究现状和发展趋势[J]. 水下无人系统学报, 2018, 26(5).

3. 冯雪磊, 李晓伟, 李锦, 等. 基于改进板块元法的标准潜艇收发分置目标强度分析[J]. 水下无人系统学报, 2018, 26(3).

4. 陈原, 郝保安, 万亚民, 等. 基于板块元法的Benchmark亮点聚类优化算法[J]. 水下无人系统学报, 2017, 25(6).

5. 陈炜彬, 段浩, 王云. 基于声固耦合算法的发射模拟试验承压结构湿模态分析[J]. 水下无人系统学报, 2017, 25(5).

6. 何心怡, 王磊, 陈菁, 等. 基于高斯声束模型的快速声场计算方法[J]. 鱼雷技术, 2016, 24(2).

TJ630.34; TB566

A

2096-3920(2020)01-0051-06

10.11993/j.issn.2096-3920.2020.01.008

周烨, 温玮, 韩建辉, 等. 基于声固耦合的水下复杂目标声散射研究[J]. 水下无人系统学报, 2020, 28(1): 51-56.

2019-06-12;

2019-06-29.

山东省重点研发计划项目资助(2016CYJS02A01).

周 烨(1995-), 男, 在读硕士, 主要研究方向为水声信号检测、处理与融合技术.

(责任编辑: 许 妍)