煤层底板岩层的渗流特性以及水岩耦合作用的理论研究

杜 琳

（大同煤矿集团同生峪沟煤业有限公司，山西 朔州036002）

当矿井底板中含有含水层时，在采场采动作用下含水层的运移变形以及稳定性演化特征是应力场和渗流场相互作用相互耦合的结果[1]。具体作用形式表现为：在围岩应力作用下裂隙岩体含水介质会发生运移变形，从而改变了岩体内部结构的力学特性，进而影响岩体的渗透特性，在宏观角度会对地下水的分流等形成影响；当岩体内部形成水体的渗流通道时，在渗流场的作用下岩体的受力特征发生改变；故本文对煤层底板岩层的渗流特性以及水岩耦合作用进行系统研究，从而为矿井防治水提供一定理论依据。

1 岩体全应力- 应变- 渗透特征

岩体内部孔隙和裂隙的发育贯通程度决定了水体的渗透通路，也就决定了岩体的渗透性；而岩体在应力作用下的变形特征也决定了内部孔隙裂隙的演化规律，故岩体在应力作用下的变形是引起其自身渗透性改变的内在因素。岩体的岩性不同，则力学特性就具有差异，在应力作用下变形特征就不同。矿井底板不同岩性岩体的渗透特性如下：

1）砂岩的渗透性较大，而泥岩的渗透性往往较小，故一般作为隔水层。

2）在峰值强度之前，随着所受应力的增大，砂岩和泥岩的渗透性也在不断增加，但强度峰值要超前于渗透峰值。

3）在不同的围压作用下泥岩渗透率的变化特征不同；当围压较小时，在峰值强度后渗透率的变化较小，而围岩较大时在峰值强度后渗透率的减小速率较快；但灰岩的渗透率受围压的影响较小。

4）通常情况下不同种类岩体的渗透性随着围岩的增大而减小，但随着渗透压力的增大而增大。

有专家学者[2]研究表明，岩体在受载过程中表现出的渗透率是应变的函数。在应变软化阶段会出现渗透率的峰值点，也就是说该峰值点要滞后与岩体破坏而出现，如图1 所示。由此可见，在矿井防治水过程中，避免岩层发生失稳破坏是固然重要的，但对于已经失稳破坏的岩体，需要避免岩体在应变软化阶段变形的进一步演化。

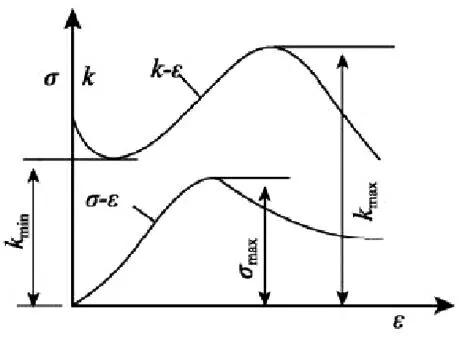
图1 岩体全应力- 应变- 渗透示意图

总体上根据岩体在应力作用下的变形特征可将其失稳过程分为六个阶段;

1）裂隙闭合阶段，在该阶段岩体在外载荷作用下内部的孔隙和裂隙逐步闭合，渗透率减小；

2）弹性变形阶段，在该阶段岩体渗透率缓慢增大；

3）裂隙扩展阶段，在该阶段岩体的体应变随着应力的增加而逐步加大，表现为渗透率的快速增大；

4）岩体失稳破坏阶段，在该阶段岩体变形以塑性屈服为主，内部裂隙不断扩展贯通，形变增加显著，体积膨胀，最终发生屈服破坏；

5）应变软化阶段，随着岩体应变的增大应力在不断减小，在阶阶段渗透率演变特征表现为峰值强度之后逐步减小；

6）残余强度阶段，在该阶段应力随着应变的增大而逐步趋于稳定。

本次研究矿井工作面底板岩层岩性以泥岩和灰岩为主。当围压较小时，未发生失稳屈服的泥岩渗透率小，具有良好的阻水性；如果泥岩在采动作用下发生失稳，当围压较大时，则泥岩内部扩展贯通的裂隙容易被压实，透水性减弱；总体上围压对灰岩渗透性的影响效果不是十分显著。

2 矿井水对应力场的影响

矿井水不仅会使底板岩层内部的裂隙发生拉应变，而且会改变岩体的应力应变特征，进而改变岩体的强度和杨氏模量。通过改变岩体内部的体积应变渗流场实现了对应力场的改变。

矿井水根据突水动力源的不同可分为静水压突水和懂水压突水。前者不受外界动力的冲击，水体储存稳定，顶板岩层容易在水体的水理作用下而逐步发生渗流；后者水压较大，会在一瞬间形成涌水通路而使得水体涌入工作面。

2.1 静水压突水的影响

静水压突水的影响主要体现在劈裂和导升两个方面。

2.1.1 劈裂

劈裂主要为对隔水层内部裂隙的破坏，在静水压作用下岩体内部裂隙的受力的对称的，裂隙在水的作用下发生张开，如图2 所示。

为了对静水压作用下的裂隙特征进行定量评价，将裂隙视为椭圆结构，长度为2a，围岩应力为σ，裂隙内部水压为p，如图3 所示。

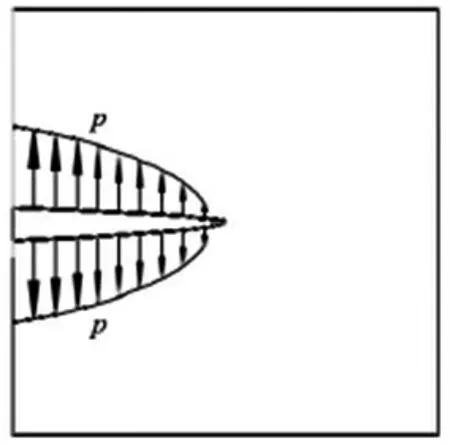
图2 岩体内部裂隙受力特征示意图

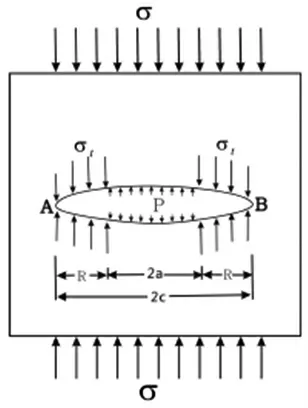
图3 岩体内部裂隙等效模型示意图

在图3 中，在静水压作用下发生扩展的裂隙面会产生抵制扩展效应的屈服应力σt，屈服区宽度为R，R=c-a。

由于屈服区端部应力没有奇异性，故裂隙尖端的应力强度因子为0，由此可得公式（1）：

通过公式（2）可以看出，随着静水压力的增大裂隙屈服区宽度也在增大，当围岩应力表现为拉应力时，裂隙容易发生扩展，而围岩应力表现为压应力时，裂隙扩展困难，因为静水压需要克服围岩应力的作用才回扩展起裂裂隙。

2.1.2 导升

在静水压力作用下，承压水会顺着岩体内部的天然裂隙导升，导升的高度为导高带。本次研究矿井底板岩层中存在一小的断层，在底板开挖过程中破坏了原有的平衡状态，底板发生弹性变形，裂隙面发生展布，在承压水作用下断层面会继续开裂，进而导致承压水导升[3]，如图4 所示，进一步建立承压水挤入岩体的等效模型，如图5 所示。

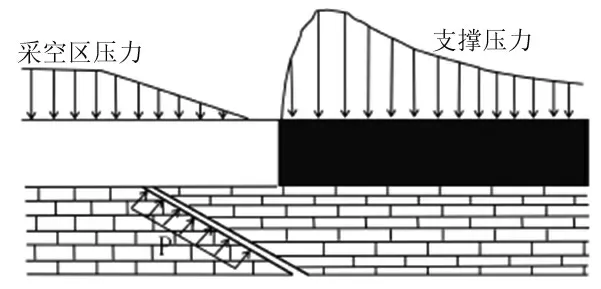
图4 底板开挖引起的导升示意图

在图5 中，裂隙起裂的方向为X 轴正向，为裂隙夹角，B 为裂隙宽度，l 为裂隙厚度，裂隙受到的水压为p，K 为裂隙面的粗糙系数，u 和ρ 分别为水的密度和流速，x 为承压水挤入裂隙的深度。则在裂隙起裂方向上有公式（3）：

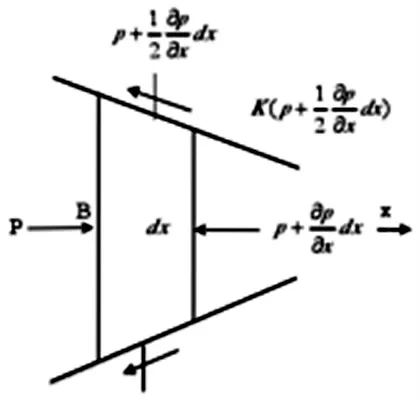
图5 底板开挖引起的导升示意图

在公式（3）中，为水流速对时间的偏导，可认为等于0，裂隙的起裂角也极小，由此可得公式（4）：

式中：p0为承压水刚开始作用于裂隙的水压。

由此可以发现，裂隙的粗糙度和宽度均会影响裂隙受到的水压，其中，裂隙受到的水压与裂隙粗糙度呈正相关关系，而与裂隙宽度呈负相关关系。通常情况下岩体内部发育的自然裂隙宽度较小，则意味着承压水挤入裂隙的深度也较小。

2.2 动水压突水的影响

动水压突水的影响主要体现在对裂隙的冲刷和对突水量的控制两个方面。

1）对裂隙的冲刷。

动水压突水的能量和压力较大，会对裂隙进行冲刷侵蚀，从而提高裂隙的过水性，对裂隙的宽度起到扩展作用，动水压突水的冲刷作用可等效为图6 所示的模型。

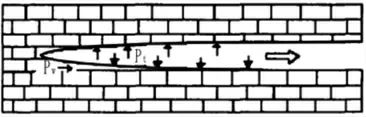
图6 动水压突水的冲刷作用等效模型示意图

在图6 中，假设动水压压力为pw，裂隙为突水通道，通道壁面上的压力为PR，直径为dR，通过通道的水量为Q，水体流速为vt，可通过公式（5）计算：

基于能量守恒定律，PR可通过公式6 计算：

式中：γw为水体的密度。压力差为ΔP=PW-PR。

由此可知压力差与流速呈正相关关系，当水流速度增加到一定值时，压力差达到了岩石的极限强度，则岩体发生失稳破坏，进而扩展的突水通路。

2）对突水量的控制。假设水流能量在突水通路中得到全部耗散，则根据达西定律可得公式（7）：

式中：K 为渗透系数；A 为通路断面面积；P 为岩溶水压；lt为渗流通路的长度。

3 应力场对渗流场的作用

有研究结果[4]显示，当岩体内部裂隙孔隙分布较为均匀时，则裂隙渗流遵循达西定律，由此可得公式（8）：

式中：V 为水流速率；J 为水力梯度。

采场采动破坏了岩体的应力平衡状态，在采场采动过程中，岩体发生运移变形，内部孔隙裂隙发生一系列的物理变化，形态和特性均发生改变，主要表现为裂隙开度和长度的改变，进而影响岩体的渗透性。为了达到应力场和渗流场的动态平衡状态，二者必须多次耦合，如图7 所示。

图7 应力场和渗流场耦合关系示意图

我们通过渗透系数来表征岩体渗透性的变化特征。基于渗透张量理论，则岩体渗透系数与裂隙开度呈正相关关系，应力场的改变影响了裂隙面的开度，进而改变的渗透系数，改变了岩体对水的渗透能力，这便是应力场对渗流场的作用机理。

4 结束语

1）在矿井防治水过程中，避免岩层发生失稳破坏是固然重要的，但对于已经失稳破坏的岩体，需要避免岩体在应变软化阶段变形的进一步演化。

2）当围压较小时，未发生失稳屈服的泥岩渗透率小，具有良好的阻水性；如果泥岩在采动作用下发生失稳，当围压较大时，则泥岩内部扩展贯通的裂隙容易被压实，透水性减弱；总体上围压对灰岩渗透性的影响效果不是十分显著。

3）随着静水压力的增大裂隙屈服区宽度也在增大，当围岩应力表现为拉应力时，裂隙容易发生扩展，而围岩应力表现为压应力时，裂隙扩展困难，因为静水压需要克服围岩应力的作用才回扩展起裂裂隙。

4）裂隙的粗糙度和宽度均会影响裂隙受到的水压。动水突水压力差与流速呈正相关关系，当水流速度增加到一定值时，压力差达到了岩石的极限强度，则岩体发生失稳破坏，进而扩展的突水通路。

5）应力场的改变影响了裂隙面的开度，进而改变的渗透系数，改变了岩体对水的渗透能力，这便是应力场对渗流场的作用机理。