自适应迭代滤波在水轮发电机组振动分析中的运用

黄冬松，吴道平，温钦钰，赵志炉

（1.能源科技工程公司，上海 200233；2.国网江西省电力有限公司电力科学研究院，江西 南昌 330096；3.华中科技大学能源学院，湖北 武汉 430074

0 引言

近年来，由于电力体制的不断改革，我国水电得到了充分的开发，并产生了巨大的经济效益。清洁，安全，价格低廉是水力发电的优点，因此，水电机组运行的稳定性成了人们关注的焦点[1-3]。水力发电机组的振动和水轮机压力脉动是衡量机组运行状态稳定性的重要指标。

水电机组在非稳态运行时，其振动信号变化较大，加上在采集过程中硬件以及环境因素的影响，得到的振动信号混杂着噪声，甚至会被噪声淹没，这对水电机组的运行监控产生了不便。

为了分析非平稳信号及从强噪声背景提取特征信号，本文提出基于独立分量分析-自适应局部迭代法的水轮机特征提取方法。非平稳信号的分析一直是众多学者研究的热点，自适应分解法能够很好的解决这个问题。从傅里叶分析[4-5]开始，到Huang[6-8]推出EMD（empirical mode decomposition）以及EEMD（ensemble empirical mode decomposition），自适应分解法得到了不同程度的发展。从小波变换入手，Gilles[9]在2013年提出了基于小波变换的EWT（empiricalwavelet transform）。在2014年，Dragomiretskiy[10]提出了VMD（variational mode decomposition）。 ALIF（adaptivelocaliterativefiltering）是Cicone[11]提出的一种基于迭代滤波[12]的分解方法，它能将信号分解成具有物理意义的分量，并且大大的提高分解精度；此外，ALIF具有很好的抗模态混叠能力，Xueli等[13]研究表明ALIF能够有效解决噪声所导致的模态混合。独立分量分析ICA（independent component analysis），一般被用作盲源分离，它通过建立目标函数将盲源信号分解，由此恢复信号[14]。因此，可先利用独立分量分析对原始信号进行分析，再结合自适应局部迭代滤波对各个分量进行分解，并分别进行自相关分析，求得归一化自相关函数及对应的能量集中度指标[15]，基于能量集中度选择有效分量并进行特征信号重构。

1 自适应迭代滤波

Cicone在2014年提出的ALIF是基于迭代滤波IF（iterative filtering）的一种新的模态分解方法。ALIF与IF的区别在于滤波所使用的Fokker－Planck方程以及增加的自适应性[16]。

1.1 迭代滤波

ALIF可以用下面的算法表示：

算法：IMF=ALIF（f）

外部循环：当极值的个数f大于2，即f>2时，

令f1=f

内部循环：当不满足终止条件时，

计算fn滤波器长度ln

内部循环结束：

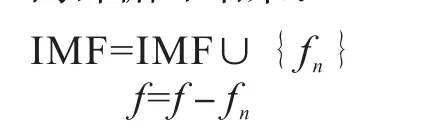
外部循环结束：

其中wn（x，t），t∈[-ln（x），ln（x）]，是滤波函数，它的长度是2ln（x）。ln（x）可以从式（1）求得

其中N为信号的长度，m为信号的极值点个数，λ为可调参数，λ∈[1，3]。对于被分解的信号，其信噪比越高，λ越大。

从上述算法中我们可以观察到，ALIF有两个循环，外部循环是为了得到，f1=∑IMFn+r（x）其中为残余项，内部循环是确定相应的IMFn。对于内部循环，迭代终止条件可用式（2）表示

对于外部循环，当r（x）满足为相应的趋势项时，即可停止循环。

1.2 Fokker－Planck方程

Fokker－Planck方程可以用式（3）表示

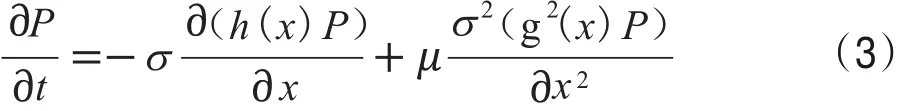
式中σ，μ∈（0，1）。我们假设h（x），g（x）都是光滑可导的函数，且h（x），g（x）∈[a，b]其中a＜0＜b，满足

（1）g（a）=g（b）=0，且对于任意x∈（a，b）均有g（x）＞0；

（2）h（a）＜0＜h（b）

在式（3）中，等号右侧第一项使得方程的解P（x）从端点a和b向（a，b）的中点聚集，而第二项使得P（x）从（a，b）向端点a和b扩散。当两者达到平衡，即

此时，方程有解P（x）且满足x∈（a，b）时，P（x）≥0；x∈（a，b）时，P（x）=0。Fokker－Planck方程的解P（x）为ALIF中的的滤波函数wn（x，t），wn（x，t）可以随着区间的改变而求解出不同的表达式。

2 独立分量分析

ICA作为基于统计的代数方法和基于信息论的迭代算法，根据算法的不同，可以分成不同的方法，本文以FastICA算法作为分析方法。设观测信号与混沌信号（原信号）函数为S（t）=[s1（t），s2（t），…，sn（t）]，对于观测信号，可以用式（4）表示

其中每个si（t）（i=1，，…，n）之间相互独立，且满足条件：

1）至多有一个服从高斯分布。

2）A为混合方阵，则A为非奇异矩阵，存在逆矩阵。

FastICA算法流程如下所示：

1）为使观测到的数据X的对其进行中心化；

2）对数据进行白化，X→Z；

3）选择需要估计的分量m，把迭代次数设为P→1；

4）选择一个初始权矢量（随机的）Wp；

5）令

6）如果Wp不收敛的话，返回5）；

7）令P=P+1，如果P≤M，则返回4）。

3 仿真信号

为了验证该方法的准确性，本文采用常见的振动倍频信号作为仿真信号进行试验。假设机组转速为，采样频率为1 024 Hz，采样时长为3 s，幅值单位为mm，具体信息如下所示：

1）1倍频源信号

S1=20*sin（t*87.5/30*π）；

2）2倍频源信号

S2=10*sin（t*87.5/15*π）；

3）50 Hz干扰信号

S3=5*sin（t*2*50*π）；

4）噪声信号

S4=randm（1，3073）；

源信号波形如图1、图2所示。

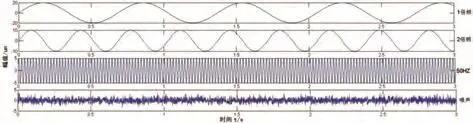
图1 源信号

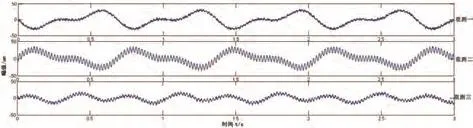
图2 观测信号

接着用一个随机矩阵A将上述几种信号混合。

经过ICA处理，结果如图3所示。

图3 ICA分解信号

对图3中的各个分解信号做ALIF分解，其中Xi设为2.2，当Xi越大，分解出的IMF所包含的噪声越少，但是所要求的滤波函数长度也就越长，对离散信号而言，则所要求的滤波函数的点数也就越多。为了筛选出有效的IMF分量，本文采用基于自相关函数的能量集中度指标EFA（energy focus abilityindex），即归一化自相关函数原点两侧的小区间内所含能量与总能量的比值：

式中归一化自相关函数的计算公式如下：

一般，噪声分量的EFA值相比于特征频率要大得多，由于需要根据EFA的大小来选择合适的IMF分量并进行重构，那么指标的边界使我们要考虑的一个关键问题。为了能得出合理的边界，本文对不同高斯白噪声强度下的ALIF分解结果的EFA进行了分析实验，其中噪声强度从5 dbw至20 dbw，ALIF的Xi从1取至3，EFA的区间取原点两侧的百分之十。由于数据较多，本文只将Xi分别为1，1.6，2.2，3时的EFA的最小值作为展示，具体如图4所示。

图4 EFA

从图4中可以观察到，EFA最小值随着Xi的增大而减少，说明Xi的大小对ALIF的滤波作用有一定的影响。其中当Xi为3时，噪声强度为5 dbw的EFA低于0.2。根据实验分析，当噪声为非高斯白噪声时，可以根据不同的Xi值来确定边界值。本文选取Xi=2.2，将边界值设为0.2。对ALIF分解的各个分量做EFA计算，以第一个分量为例，具体如表1所示。

表1 IMF的EFA值

从表1中可以看出，满足EFA小于0.2的只有第6个IMF，因此我们选取IMF6作为有效分量。采用相同方法对其余分量进行筛选，如图5所示。（图中忽略噪声分量）

图5 仿真信号ICA-ALIF处理结果

由图5可知，本文所提方法成功的将相关噪声过滤，并提取出相应的特征分量。

4 实例分析

本实例采用某电站实际采集到的上导信号，该机组信息为水轮机额定出力120 MW，额定转速为75 rpm。采样频率为1 024 Hz，截取的时长为3 s。信号具体如图6-9所示。

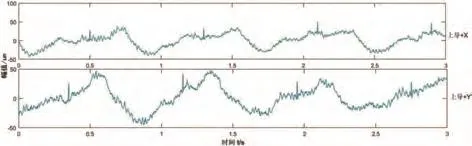
图6 上导信号

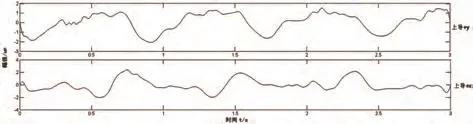
图7 ICA-ALIF分解

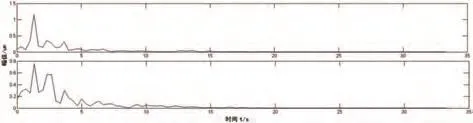
图8 ICA-ALIF频谱图

图9 仅ALIF分解频谱图

为说明该方法的有效性，分别采用该方法与无ICA的ALIF分解的结果作为对比。从图8，图9中我们可以看出只有ICA-ALIF分解可以将上导信号中的0.5倍频、1倍频、2倍频、3倍频分解出来，单纯的ALIF分解在虽然能将1倍频、2倍频提取出来，但无法将0.5倍频提取，并且在3倍频特征提取方面并不清晰，在降噪方面与ICA-ALIF有一定的差距。

5 结语

通过上述仿真与实验，本文提出的一种基于自适应迭代滤波与独立分量分析的降噪以及特征提取的方法，并得出如下结论：

1）信号通过独立分量分析，可以将多通道混合的源信号中的噪声去除，并突出特征信号。

2）采用基于自相关函数的能量集中度指标在筛选相关模态分量可以将含有噪声分量较多的模态去除，并保留相关特征模态。

3）采用自适应迭代滤波与独立分量分析相结合的方法能有效的去除水轮机振动信号中的异常噪声并使曲线变得更为平滑，准确、全面、高效的将突变特征提取出来。该方法与传统方法相比，在降噪和特征提取方面有着明显的优势，可以更有效的解决和满足实际工程的需求。