基于动态伪装网络的主动欺骗防御方法

王硕，王建华，裴庆祺，汤光明，王洋，刘小虎

（1.信息工程大学密码工程学院，河南 郑州 450001；2.西安电子科技大学综合业务网理论及关键技术国家重点实验室，陕西 西安 710071；3.西安电子科技大学陕西省区块链与安全计算重点实验室，陕西 西安 710071）

1 引言

随着网络应用的广泛普及以及支撑技术的不断发展，云计算、智能设备、区块链、物联网等不断涌现的新技术正在深刻改变人们的生活，推动社会的飞速发展。然而，与此同时，伴随网络而来的安全问题也越发严重。据国家计算机网络应急技术处理协调中心2018 年度网络安全工作报告显示[1]，2018 年，我国境内感染计算机恶意程序的主机数量约为1 256 万个，规模在100 个主机以上的僵尸网络数量达3 143 个，规模在10 万个主机以上的僵尸网络数量达32 个，WannaCry 蠕虫病毒事件爆发等。然而，在众多网络攻击形式中，渗透攻击威胁尤其巨大，特别是以高级持续攻击（APT,advanced persistent threat）为代表的渗透攻击，给人们带来了巨大的威胁。传统的网络防御以“筑高墙、堵漏洞、打补丁”为主，手段单一被动，不能有效应对新型攻击形式，且存在“攻防不对称”的严重劣势。

网络欺骗防御是改变“攻防不对称”劣势的创新思路，已成为当前网络安全防御的研究热点和重要研究方向之一[2-3]。它的核心思想在于：防御者在己方目标网络中布设骗局，干扰、误导攻击者对己方网络系统的认知，使攻击者采取对防御方有利的动作，从而有助于发现、延迟或阻断攻击者的活动，达到防护目标网络的目的[4]。美国提出的移动目标防御（MTD,moving target defense）[5-6]是增加攻击者的认知难度，而网络欺骗是干扰攻击者的认知，甚至使攻击者产生错误认知，显然网络欺骗相对移动目标防御层次更高，目标更远。也有学者称网络欺骗是“后移动目标防御时代”。2016 年，Springer出版社出版了《Cyber Deception》[7]，这是第一本专门介绍网络欺骗研究的著作，汇集了最新的网络欺骗研究成果。网络欺骗不是一种具体的防御技术，而是由蜜罐演进而来的一种防御思想。

现有研究可将蜜罐分为狭义的蜜罐和广义的蜜罐。狭义的蜜罐作为传统意义的蜜罐，用来模拟服务或服务器等网络资源。根据交互水平，狭义的蜜罐可分为低交互蜜罐、中交互蜜罐和高交互蜜罐。Provos[8]提出了一种低交互蜜罐，通过模仿网络堆栈行为来欺骗nmap 等指纹识别工具。此外，一些学者也提出了用于应用层协议的蜜罐，如Telnet[9]和HTTP[10]，还有一些针对特殊设备的蜜罐，如智能手机[11]、USB 设备[12]和数据采集装置[13]。广义的蜜罐则是基于蜜罐这种模拟思想，针对相对广泛的对象来模拟一些伪造的对象，从而达到欺骗攻击者的效果。Juels 等[14]提出一种Honeywords 方法，通过构造虚假账户密码来检测用该密码尝试攻击的攻击者。Araujo 等[15]提出一种Honey-patches方法，通过巧妙设计虚假漏洞补丁来欺骗攻击者。Conroy 等[16]提出利用虚假新闻来欺骗攻击者。Lee等[17]则提出在社交网络上设计蜜罐来欺骗垃圾邮件制造者。Lazarov 等[18]提出用虚假的URL 地址欺骗攻击者。加密消息也被用来吸引并欺骗攻击者[19-20]。广义的蜜罐形式多种多样，理论上只要攻击者对网络中某一个对象有兴趣，则可依据该对象伪造一个虚假的对象，达到欺骗攻击者的目的。

此外，为了提高蜜罐的隐蔽性，避免其被攻击者识破，Clark 等[21]通过周期性地改变蜜罐节点的IP 地址，使攻击者已识别出的蜜罐IP 失效，从而增加蜜罐节点的安全性。Sun 等[22-23]将IP 随机化与伪造欺骗节点巧妙结合，在目标网络中放置蜜罐节点，并通过真实节点与蜜罐节点的IP 随机化来干扰攻击者。Venkatesan 等[24]提出利用强化学习来部署检测器和蜜罐，实现最优化地去除僵尸节点的目的。然而该方法学习周期过长，模型训练较难。石乐义等[25]提出基于动态阵列蜜罐的协同部署方法来达到干扰和防范攻击者的目的。然而上述几种方法往往不考虑防御成本，从而导致实用性较低。为了获得有限防御成本下的最优欺骗策略，一些学者[26-30]用博弈论思想描述攻防对抗过程，并用纳什均衡解作为最优欺骗策略，取得了较好的效果。然而大多研究仅考虑纳什均衡的纯策略而忽略了混策略。事实上，混策略由于其特有的随机性更能使攻击者产生不确定性，更适合于欺骗防御攻防场景。

基于以上分析可知，当前的渗透攻击往往是针对特定目标的定向攻击，持续时间长且隐蔽性强。现有蜜罐很容易被攻击者识破而失效。为了实现对渗透攻击者的最大化欺骗，本文提出一种基于动态伪装网络的主动欺骗防御方法。动态伪装网络包括真实网络和伪装网络，其中伪装网络是依据真实网络而创建的虚假网络。首先，基于动态伪装网络描述了攻防对抗场景。该场景中，借助动态伪装网络，防御者通过向攻击者发送伪装信号，从而使处于真实网络中的攻击者受到威慑而放弃攻击，并使处于伪装网络中的攻击者受到欺骗而攻击虚假目标，从而实现对真实网络的更好防护。其次，为了最大化防御收益，将攻防双方对抗过程用信号博弈模型进行描述，设计了基于双层威胁渗透图的攻防策略收益量化方法；进而提出了一种统一纯策略与混策略的精炼贝叶斯纳什均衡求解方法，利用精炼贝叶斯纳什均衡作为最优欺骗策略，实现了防御收益的最大化。最后，实验表明了本文方法的有效性，并在分析实验结果的基础上提出了针对性的主动欺骗防御规律及建议。

2 基于动态伪装网络的主动欺骗攻防场景

一般来讲，蜜罐主要通过布置一些作为虚假的主机、网络服务或者信息，致使攻击方对其实施攻击，从而捕获攻击者信息。多个蜜罐组成的模拟网络称为蜜网，其本质仍是蜜罐，反而有时更容易被攻击者识破。然而事实上，对于真正高水平的渗透攻击者，其不仅对目标网络有一定的了解，且其攻击目标非常明确，为了不暴露自己的攻击痕迹，攻击者仅对自己的攻击目标感兴趣，如“震网”病毒没有发现攻击目标时，其一直保持“静默”，直到满足攻击条件。面对该种攻击者，传统的蜜罐或蜜网很难引起攻击者的兴趣且容易被其识别，往往不能达到欺骗攻击者的目的。基于上述考虑，为了进一步提高欺骗环境的真实性而达到欺骗攻击者的目的，本文提出一种基于动态伪装网络的主动欺骗防御方法。动态伪装网络的定义如定义1 所示。

定义1动态伪装网络（DCN,dynamic camouflage net）DCN=(G,G′)。对一个特定的真实网络G，动态实时地模拟真实网络G中节点、拓扑、功能及数据等，创建用于欺骗攻击者入侵而获得攻击者知识的伪装网络G′。其中G′可以是真实的物理网络，也可以是利用软件定义网络（SDN,software defined network）及虚拟化的容器技术创建的网络。动态伪装网络的拓扑示例如图1 所示。

图1 动态伪装网络的拓扑示例

由定义1 及图1 可知，与传统的蜜罐或蜜网不同，DCN 近似完美地“复制”真实网络G，真实网络中的每一个节点都能在伪装网络G′中找到它的“影子”节点，其真实性更高，对攻击者的干扰性也更强，更易实现欺骗攻击者的目的。然而，通常情况下，真实网络运行着正常的业务活动或为合法用户提供服务，其系统活跃性较高；相反，伪装网络尽管与真实网络相似，但由于伪装网络是专门为攻击者打造的，缺少正常的网络业务活动，其系统活跃性相对较低，一旦有用户访问伪装网络，则认为该用户为攻击者。该问题也导致攻击者会依据所在网络的系统活性来分辨其所处的网络类型，防止被欺骗。

鉴于此，本文深入分析该攻防场景，利用主动欺骗思想，设计了一种基于动态伪装网络的主动欺骗防御方法。该方法中，借助动态伪装网络，防御者向攻击者发送伪装信号，使处于真实网络中的攻击者受到威慑而放弃攻击，并使处于伪装网络中的攻击者受到欺骗而攻击虚假目标，从而实现对目标网络的更好防护。基于动态伪装网络的主动欺骗攻防场景如图2 所示。

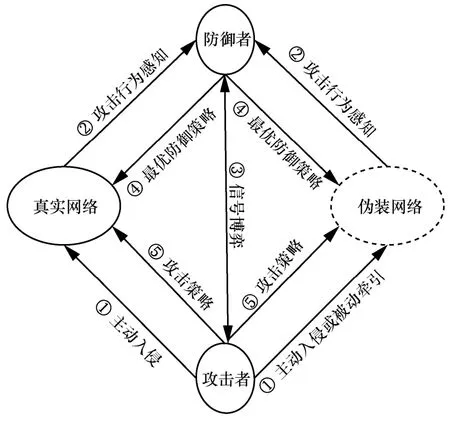
图2 基于动态伪装网络的主动欺骗攻防场景

依据图2，基于伪装网络的网络主动欺骗攻防场景可分为以下5 个步骤。

Step1攻击者为了达到攻击目标，需要对目标网络进行持续渗透，在渗透过程中，攻击者可能入侵真实网络或者伪装网络。此外，防御者可通过流量牵引的方法，将处于真实网络中某一节点的攻击者牵引到伪装网络中对应的节点，从而实现攻击者由真实网络到伪装网络的被动牵引。

Step2防御者通过分析网络产生的告警来实现对攻击者的行为感知，进而推断攻击者当前所处的节点及攻击目标。

Step3一方面，攻击者通过分析所在网络的系统活性来识别该网络类型，进而决策下一步的攻击；另一方面，防御者可发送伪装信号来干扰攻击者（通过减少或暂停部分网络活动来降低真实网络的系统活性，或通过伪造虚假的流量来提高伪装网络的系统活性），使攻击者无法正确识别其所处的网络类型。在此过程中，攻击者与防御者展开博弈，该博弈过程可用信号博弈模型描述。

Step4依据博弈结果，防御者选取最优的防御策略，即是否发送伪装信号。

Step5依据博弈结果，攻击者选取最优的攻击策略，即是否对攻击目标发动攻击。

3 信号博弈模型

任何实用的防御策略均需要考虑防御收益，博弈论是网络安全领域公认的定量分析攻防对抗收益的有力工具。在基于动态伪装网络的网络主动欺骗防御攻防场景中，网络类型对攻击策略有着重要的影响：若攻击者处于真实网络中，它将继续渗透最终实现攻击目标；若攻击者处于伪装网络中，它将放弃攻击以减少毫无意义的攻击花费。事实上，攻击者并不知道其所处网络的类型，而需通过探测所处网络的系统活性来推断网络类型；防御者可通过发送伪装信号来干扰攻击者的推断。已有研究表明，信号博弈模型可以使防御者通过主动选择及发送伪装信号，实现对攻击者的欺骗、干扰，提升主动欺骗防御能力，适用于本文提出的攻防场景，能够为防御者选取最优防御策略提供指导。

3.1 信号博弈模型定义

作为不完全信息动态博弈的一种，信号博弈能够准确描述不确定信息对攻防策略选择的影响。由第2 节的攻防场景描述可知，攻防对抗过程是一个非合作、不完全信息、多阶段、动态博弈的过程。因此，该过程可用信号博弈模型来描述，定义如下。

定义2信号博弈模型（SGM,signaling game model）是一个五元组，即SGM=(Ω,Θ,S,P,U)，各变量具体定义如下。

1)Ω={Ωd,Ωa}为局中人集合，Ωd为防御者，作为信号发送者；Ωa为攻击者，作为信号接收者。

2)Θ={N,H}为防御者类型空间，在该攻击过程中，防御者类型可认为是攻击者所处的网络类型，N表示攻击者处于真实网络G，H表示攻击者处于伪装网络G′。攻击者并不知道其所处的网络类型，其仅有对自己所处网络类型的先验概率。

3)S={D,A}为防御者与攻击者的行动空间。其中，D={d1,d2}为防御者的行动空间，d1代表维持和真实网络相似的较高的系统活性，d2表示维持和伪装网络相似的较低的系统活性。具体来讲：①当防御者类型为N时，防御者一方面可不采取任何动作来实现行动d1，另一方面可通过减少或暂停部分网络活动来降低真实网络的系统活性，使真实网络看起来与伪装网络相似，从而来实现行动d2；② 当防御者类型为H时，防御者一方面可通过伪造虚假的流量来提高伪装网络的系统活性，使伪装网络看起来与真实网络相似，从而来实现行动d1，另一方面可不采取任何动作来实现行动d2。A={a1,a2}为攻击者的行动空间，a1表示攻击者选择入侵，a2表示攻击者选择不入侵。

4)P:Θ↦[0,1]×[0,1]为攻击者对防御者类型的先验概率。P=[p,1-p]，其中p=P(Θ=N)表示防御者类型是真实网络的概率，1-p=P(Θ=H)表示防御者类型是伪装网络的概率。

5)U={ud,ua}为防御者和攻击者的收益函数。

本文所提信号博弈模型主要分为4 个阶段。

1)自然以概率分布(p,1-p)从防御者类型空间Θ={N,H}选择防御者类型，即P(Θ=N)=p∈[0,1]，P(Θ=H)=1-p∈[0,1]。

2)由于目标网络入侵检测系统的存在，防御者能够实时感知攻击者所处的网络类型。当防御者观察到防御者类型后，从伪装信号集D={d1,d2}中选择一个信号进行执行。

3)攻击者不能观测到防御者类型，但能观测到防御者发送的信号，然后从攻击行动集A={a1,a2}中选择一个动作。

4)攻防双方得到收益函数U={ud,ua}，收益函数的设定原则为回报与花费之差。

图3 给出了本文所提信号博弈模型的一种扩展式描述。图3 中的每一个分支表示一种博弈情况，由虚线连接的节点构成一个信息集。由于攻击者不能确定防御者的类型，因此攻击者不能区分信息集中的节点属于哪一种防御者类型。图3 中包含了2个信息集，一个是d1信息集，另一个是d2信息集。

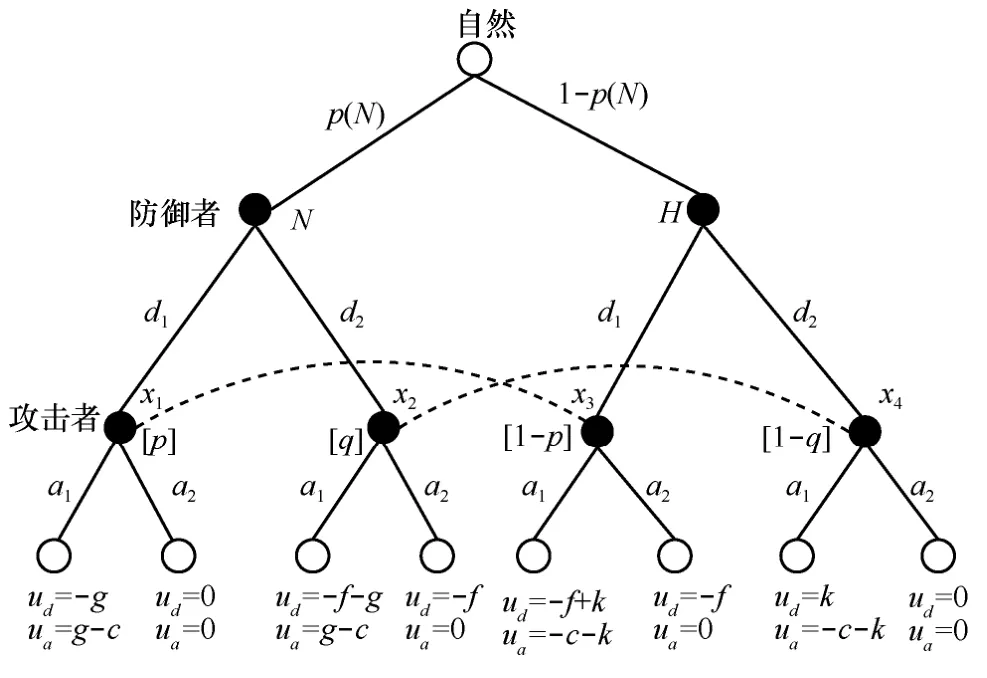
图3 信号博弈的扩展式表述

对于防御者来讲，当防御者类型为N，即攻击者当前所处的网络为真实网络时，若防御者执行行动d1，表示防御者没有采取任何动作，其花费为0；若防御者执行行动d2，表示防御者减少或暂停部分网络活动来降低真实网络的系统活性，需要一定的花费。同样，当防御者类型为H，即攻击者当前所处的网络为伪装网络时，若防御者执行行动d1，表示防御者伪造虚假流量来提高伪装网络的系统活性，需要一定的花费；若防御者执行行动d2，表示防御者没有采取任何动作，其花费为0。为了简化，假设处于真实网络中的防御者减少或暂停部分网络活动来降低真实网络系统活性所需的花费与处于伪装网络中的防御者伪造虚假流量来提高伪装网络系统活性所需的花费相同，统一记为f。

对于渗透攻击的攻击者来讲，攻击者入侵的最终目标往往是获得目标网络中一个攻击目标节点的Root 权限，如入侵目标网络的数据库服务器进而获得机密数据。不妨设攻击者的攻击目标节点价值为g，则攻击者入侵真实网络中的攻击目标节点成功时，其获得收益g，付出的攻击代价记为c，显然，此时防御者便失去了价值g。相反，若攻击者入侵了伪装网络中的攻击目标节点时，由于伪装网络和真实网络的拓扑相同，其付出的攻击代价同样为c，然而攻击者在伪装网络中获取的数据只能是虚假数据，其攻击收益为0。此外，该种情况下，由于入侵伪装网络，攻击者的身份等信息会暴露给防御者，对攻击者造成一定的损失，记为k，显然，此时防御者可得到收益k。一般来说，k的值相对较小，本文假设g＞k，f＞k。

在图3 中，当防御者类型为N，防御者和攻击者分别采取策略(d1,a1)时，防御者的收益为-g，攻击者的收益为g-c；当防御者类型为N，防御者和攻击者分别采取策略(d1,a2)时，防御者的收益为0，攻击者的收益为0。其他情况的攻防双方收益不再赘述。

3.2 基于双层渗透威胁图的攻防策略收益量化

3.1 节给出了攻防双方的信号博弈模型，依据博弈均衡理论可知，该博弈模型的纳什均衡能够给出攻防双方的最优策略。而事实上，博弈模型的均衡结果往往取决于攻防双方的收益函数。因此，如何准确量化博弈模型中攻防双方的收益函数成为选取最优防御策略的关键。依据图3 可知，本文信号博弈模型中，有4 个需要量化的参数：真实网络中攻击目标节点的价值g、攻击者入侵伪装网络产生的损失k、防御者发送伪装信号所需的代价f和攻击者渗透过程花费的攻击代价c。由于前3 个参数的设定相对简单，可依据网络自身价值以及攻击者知识直接量化。攻击者渗透过程花费的攻击代价c往往与网络中的漏洞难易程度、攻击者能力及攻击者所处的网络位置等因素有关，不能直接设定。鉴于此，为了准确量化该参数，本文提出基于双层渗透威胁图（TLTPG,two-layer threat penetration graph）的攻击代价量化方法。双层渗透威胁图是一个双层图结构，下层为主机威胁渗透图（HTPG,host threat penetration graph），描述了目标网络中任意2 个主机间的微观渗透场景；上层为网络威胁渗透图（NTPG,network threat penetration graph），描述了目标网络中各主机之间的宏观渗透关系。

定义3主机威胁渗透图GHTPG=(NHTPG,EHTPG)。NHTPG表示节点，用＜Host,Privilege＞表示，描述攻击者获得的主机权限，其中Host 表示攻击者已渗透的主机，可用该主机的IP 地址表示，Privilege 表示攻击者获得的主机权限，分为User 和Root；EHTPG表示边，用于描述单步渗透攻击，用＜Service,Vulnerability,Probability＞表示，其中Service 表示渗透攻击所利用的主机服务，Vulnerability 表示渗透攻击所利用主机服务上的漏洞，一般用公共漏洞和暴露（CVE,common vulnerability and exposure）编号表示，Probability 表示渗透攻击成功的概率。

定义4网络威胁渗透图GNTPG=(NNTPG,ENTPG)。NNTPG表示节点，描述主机标识，一般用主机的IP地址表示；ENTPG表示边，描述主机间渗透成功概率，用＜UP,RP＞表示，其中UP表示从源主机渗透获得目的主机User 权限的概率，RP表示从源主机渗透获得目的主机Root 权限的概率，二者均为0～1之间的实数。

图4 展示了一个简单的TLTPG 实例。相对于传统的攻击图，TLTPG 通过分层，宏观与微观相结合，有效减少了由于生成全局攻击图造成的高计算复杂度和空间复杂度，便于量化及计算面向渗透攻击的攻击代价。

TLTPG 能够给出目标网络中任意2 个主机的直接渗透成功概率，在此基础上，文献[31]给出了任意2 个主机间的最优渗透路径的生成方法。由于攻击者在入侵时，总希望付出较少的攻击代价，因此可假设攻击者进行渗透攻击时，会沿着最优渗透路径传输。此外，TLTPG 给出了渗透成功概率，而事实上，攻击代价与渗透成功概率有着重要的联系。一般人们认为，渗透成功概率越高，攻击代价越低；相反则攻击代价越高。渗透成功概率是依据通用漏洞评分系统（CVSS,common vulnerability scoring system）和网络拓扑量化得来，可信度较高，也得到学者的广泛认可。然而，针对攻击代价量化评估的相关研究较少，大多依据专家经验，准确度不高。因此，通过渗透成功概率来间接量化攻击代价是一种合理的方法。鉴于此，本文研究得出一种利用渗透成功率量化攻击代价的新方法。不妨设当攻击者从节点ni入侵节点nj时，其攻击成功率为sij，其需要的攻击代价记为cij。则在同一个TLTPG 中，cij的量化需要满足以下2 个条件。

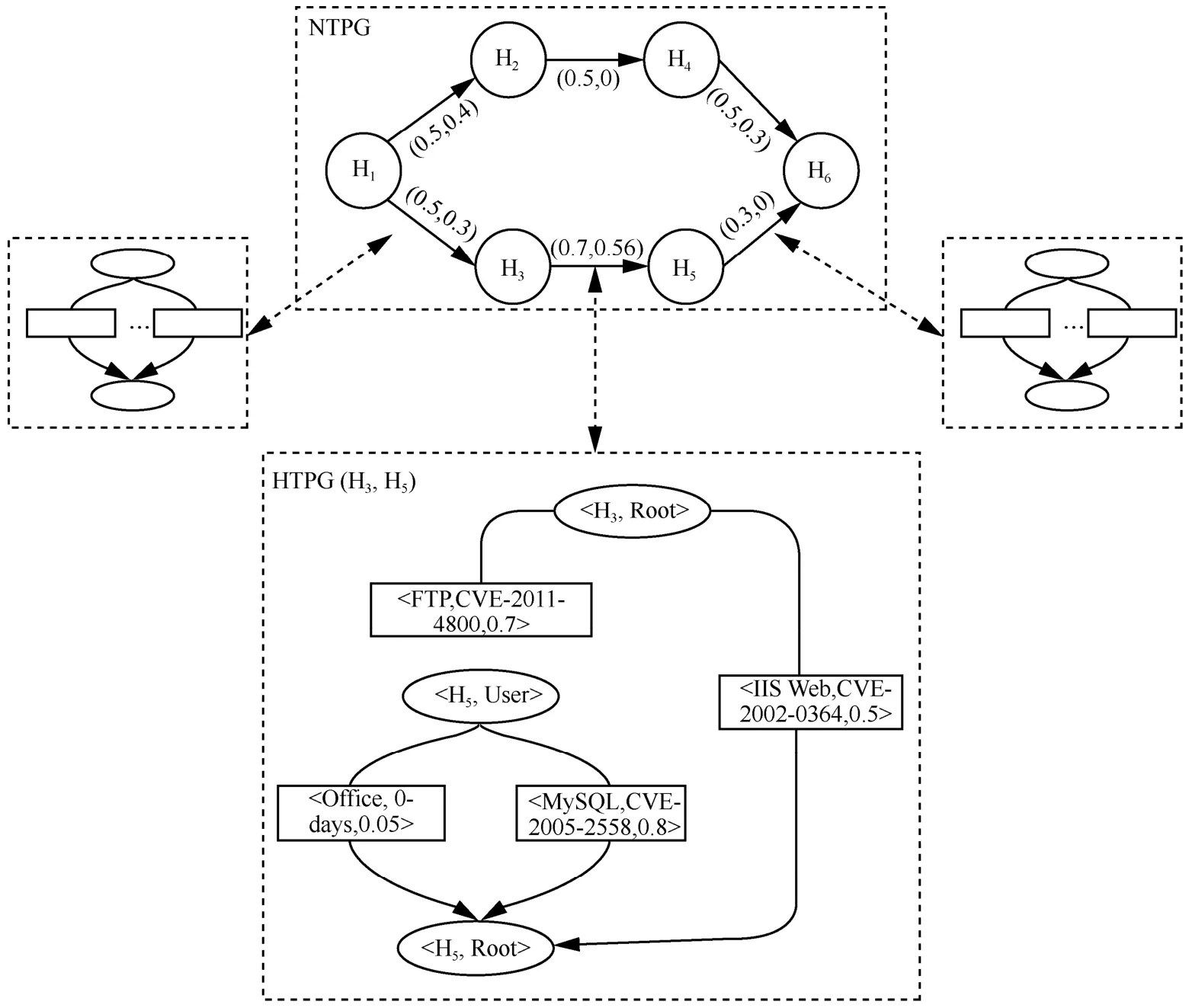
图4 一个简单的TLTPG 实例

1)对于任意2 个渗透动作eij（攻击者从节点in入侵节点nj）和epq（攻击者从节点np入侵节点nq），若sij≤spq，则cpq≥cij。

2)对于任意2 条攻击路径pathij=ni→nx→ny→ …→nz→nj和pathpq=np→→ …→→nq，若存在，则有。

定理1当时，其中κ为一正值，可用cij来表示攻击者能力系数，其满足上述2 个条件。

证明

证毕。

4 精炼贝叶斯纳什均衡求解及最优欺骗防御策略选取

信号博弈作为一种不完全信息动态博弈，其对应的纳什均衡为精炼贝叶斯纳什均衡。纳什均衡的存在性定理表明，任何一个有限博弈都至少存在一个纳什均衡（纯策略和混策略）[32]。然而，许多学者在分析信号博弈的均衡过程中，为了简化均衡求解过程，往往通过主观限定条件，仅仅考虑纯策略（包含分离策略和混同策略），忽略混策略。这种情况往往会遗漏最优策略。除此之外，由于混策略可看成纯策略的随机组合。在混策略中，局中人在博弈前通过随机装置确定自己的策略，如上抛一枚硬币等，其他局中人便不能观测到其行为，这增加了对方的不确定性，更适合于欺骗防御攻防场景。鉴于此，本文提出一种统一简洁的精炼贝叶斯纳什均衡求解方法，该方法能将纯策略与混策略统一起来求解，且求解方式快速简洁。

定义5信号博弈模型（SGM,signaling game model）具有精炼贝叶斯纳什均衡EQ=(d*(θ),a*(d),，其中d*(θ)为防御者的类型依存信号策略，表明防御者类型为θ Θ∈ 时，其执行的伪装信号策略为d*()θ；a*(d)为攻击者的依存信号策略，表明攻击者在接收到防御者发送的信号d时，其执行的攻击策略为a*(d)；为攻击者在接收到防御者发送的信号d后，判断防御者类型的后验概率。该均衡满足以下3 个条件。

1)a*(d)=。

2)d*(θ)=。

依据定义5，本文的精炼贝叶斯均衡的求解方法可分为4 步。

1)攻防双方策略形式化表示

若防御者的策略为：当节点类型为N时，以概率e1发送信号d1，以概率1-e1发送信号d2；当节点类型为H时，以概率e2发送信号d1，以概率1-e2发送信号d2。则该策略可形式化表示为。

若攻击者的策略为：当接收到信号d1时，以概率τ1选择动作a1，以概率1-τ1选择动作a2；当接收到信号d2时，以概率τ2选择动作a1，以概率1-τ2选择动作a2。则该策略可形式化表示为。

2)攻击者对防御者类型的后验概率确定

攻击者对防御者类型的后验概率的确定由其先验概率与防御者策略决定，并依据贝叶斯定理推断得出。

不妨设先验概率p(N)=p，则p(H)=1-p。当防御者采取策略时，由贝叶斯定理知

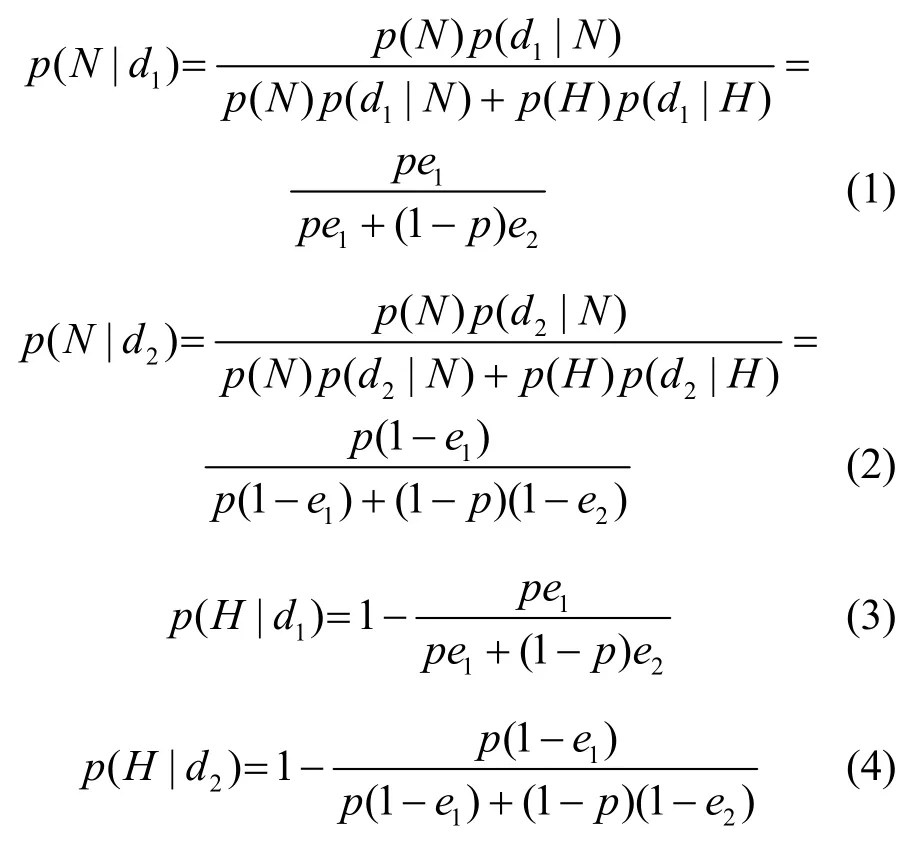
3)防御者最优策略判定

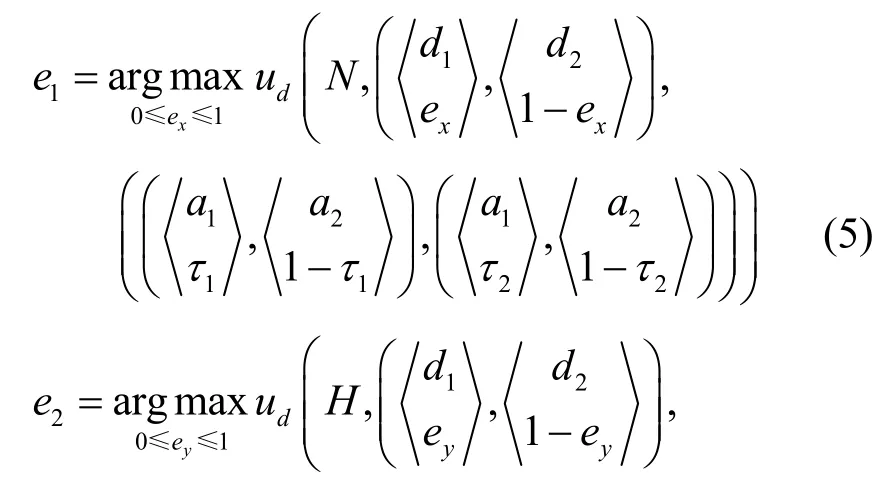
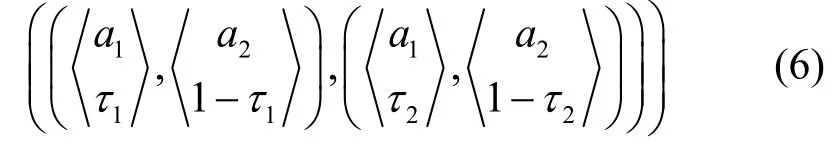
进而可化简为

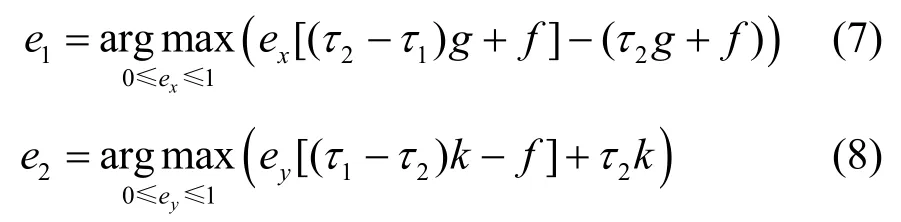
4)攻击者最优策略判定

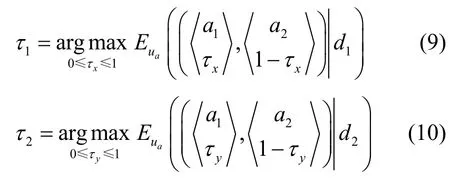
进而可化简为

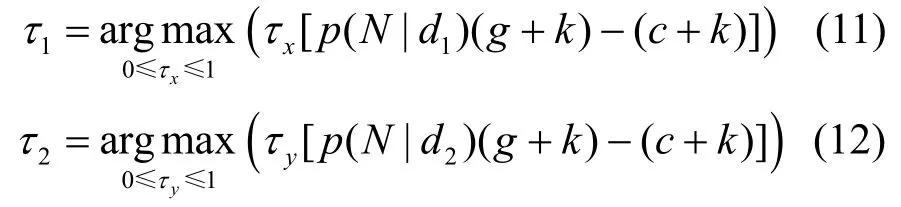
不妨令

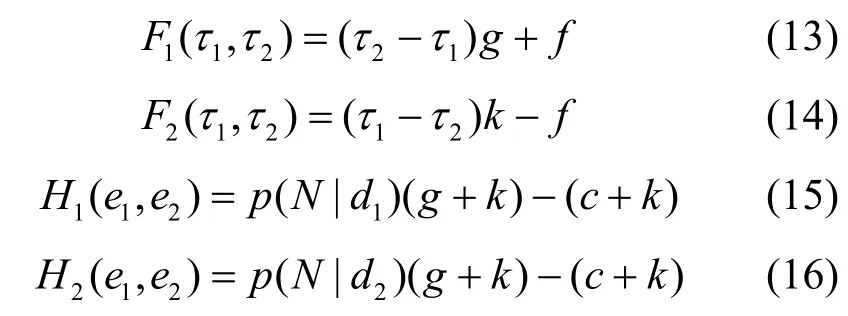
由一次函数单调性可知

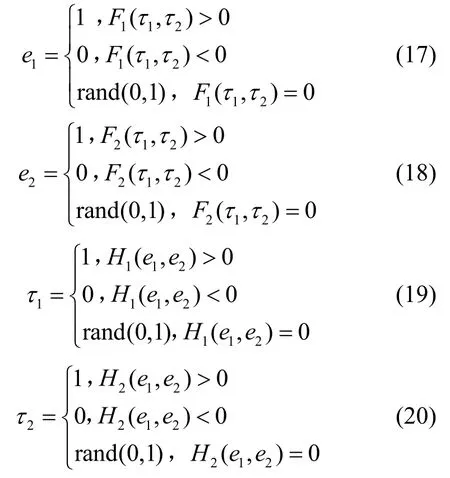
其中，rand(0,1)表示0～1 之间的任意值。显然，任意一组 (e1,e2,τ1,τ2)解，均可构成一个纳什均衡

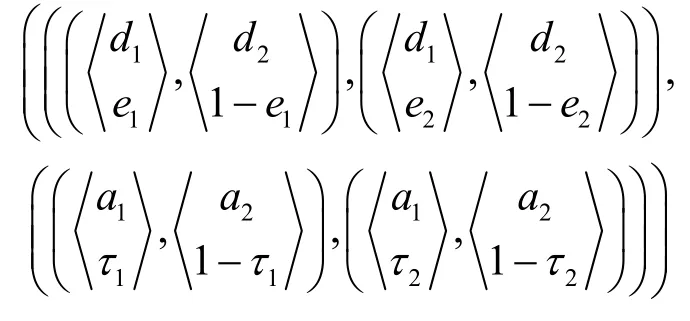
例如，当满足

时，可得(e1,e2,τ1,τ2)=(0,0,1,0)，此时存在均衡((d2,d2),(a1,a2))。式(21)可化简为

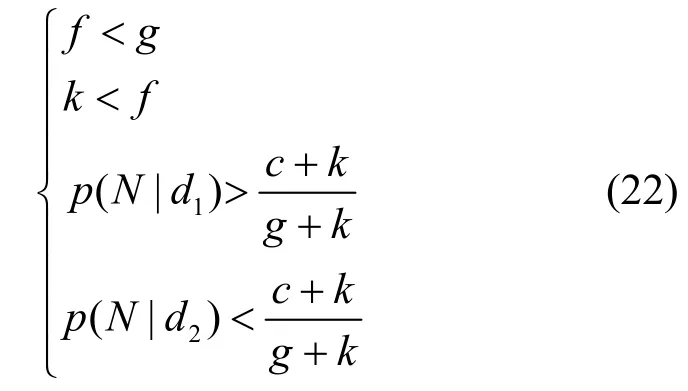
于是，当满足式(22)时，存在均衡((d2,d2),(a1,a2))，显然，该均衡为纯策略。同理可求得该信号博弈模型中的所有纳什均衡。特别地，当 (e1,e2,τ1,τ2)的解中不存在rand(0,1)时，其对应的纳什均衡为纯策略纳什均衡；反之，当 (e1,e2,τ1,τ2)的解中存在rand(0,1)时，其对应的纳什均衡为混策略纳什均衡。最终计算得出，本文信号博弈模型存在的所有纳什均衡如表1 所示。表1 纳什均衡中e1、e2、τ1、τ2的解均可视为rand(0,1)。

表1 不同网络攻防状态条件下的所有精炼贝叶斯均衡解

表1 展示了不同网络攻防条件下的所有精炼贝叶斯纳什均衡解。由纳什均衡的存在性定理知，对于不同的网络攻防条件，必存在纳什均衡解，而该均衡解便可作为最优欺骗防御策略。此外，在本文的攻防博弈模型中，防御者先于攻击者做决策，即防御者具有“提前选择”优势[27]。若存在多重均衡问题，一方面防御者可依据最大化自己的收益来选择策略；另一方面由于混策略具有干扰攻击者的作用，适用于欺骗防御策略，在收益相同的条件下，防御者可倾向于采用混策略。当防御者采用混策略时，需要根据实际情况使用一种随机装置，而该种随机装置最好不要让攻击者知道。

5 实验与分析

5.1 实验环境描述

为了验证本文方法的有效性，搭建了一个实际网络环境来进行测试。实验网络拓扑如图5 所示。

实验网络主要由2 个网络构成，即真实网络和伪装网络。伪装网络是依据真实网络构造的，其拓扑与真实网络保持一致。两者之间的唯一差别在于真实网络部署着真实的数据且运行着正常的业务活动，而伪装网络部署着虚假的数据且没有运行正常的业务活动。攻击者可利用Internet 访问真实网络。2 个网络都可分为4 个区域，分别是DMZ 区、子网1、子网2 和子网3。DMZ 区有一台Web 服务器。子网1 有2 台设备，分别是一台Pad 和一台主机，可连接Internet。子网2 有2 台主机，不能连接Internet。子网3 包括3 台服务器，分别是打印服务器、文件服务器和数据服务器。网络中的服务访问规则如表2 所示。其中，攻击者为Internet 中的一台主机。通过Nessus 漏洞扫描器对网络中各网络段进行扫描，得到各主机中漏洞信息，结合CVSS，得到表3 所示的各主机信息及其所含漏洞信息。特别地，Pad和Host1并不能通过网络访问内网的Host2和Host3，但由于人为操作不当的因素，可通过USB等传输设备连接到Host2和Host3。

5.2 均衡求解与防御策略选取

依据渗透威胁图的生成方法[31]可知，整个目标网络的网络威胁渗透关系如图6 所示。攻击者能够利用漏洞在网络中不断渗透，此外，防御者可利用流量牵引的方法将攻击者从真实网络中的一个节点牵引到伪装网络中对应的节点中。经过实验测试，流量牵引的过程时延为毫秒级，故本文假设其不会被攻击者发现。进一步，参考文献[26-27]的赋值方法，不妨设攻击者的攻击目标是入侵数据服务器并获取机密数据，其价值设为100，即g=100。攻击者入侵伪装网络产生的损失为20，即k=20。防御者发送伪装信号所需的代价为30，即f=30。依据图6 可得目标网络中任意节点之间的最优渗透概率，进而可利用3.2 节的方法来定量刻画攻击者从一个节点到另一个节点所需的攻击代价，不妨设攻击者能力系数κ=30。最初，外部攻击者成功入侵数据服务器的最优渗透路径为攻击者→Pad→Host3→数据服务器，故其渗透成功概率为0.6×0.32×0.6=0.115 2，则在此过程攻击者需要花费的攻击代价为c=28。不妨设防御者类型为真实网络的概率p=0.7，则处于外部的攻击者与防御者展开信号博弈，纳什均衡为EQ4，其中e1=0.714，τ2=0.7。由均衡结果可知，在此场景下，防御者的最优策略为：真实网络以0.714 的概率发送信号d1，以0.286 的概率发送信号d2（模拟伪装网络特征）；伪装网络则发送信号d2。随着攻击者的渗透过程，攻击者在网络中的位置会不断深入，本文分析了当攻击者处于不同节点时的精炼贝叶斯均衡结果，如表4 所示。

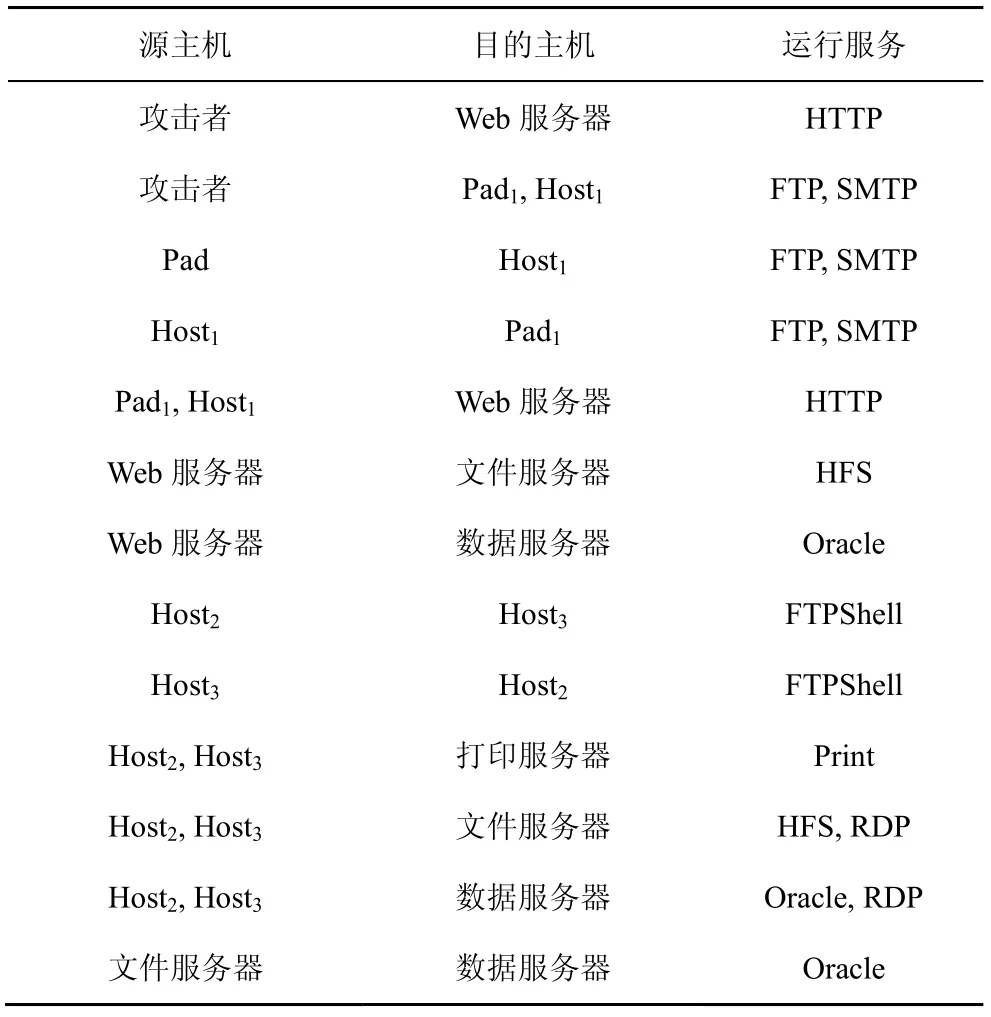
表2 网络中的服务访问规则

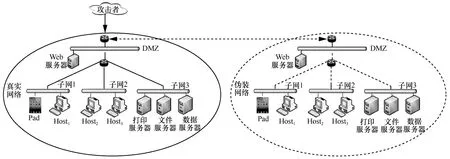
图5 实验网络拓扑

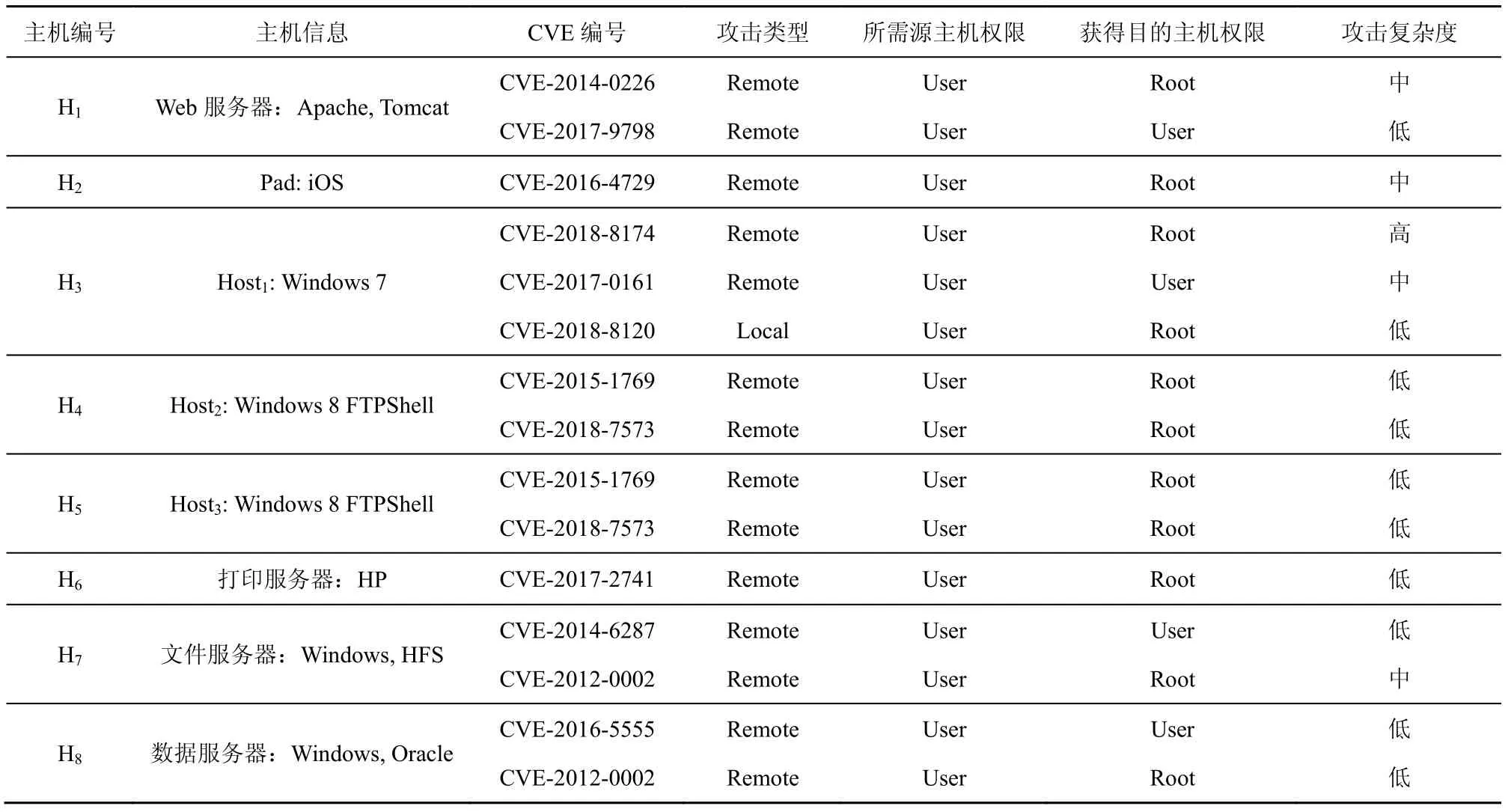
表3 各主机信息及其所含漏洞信息

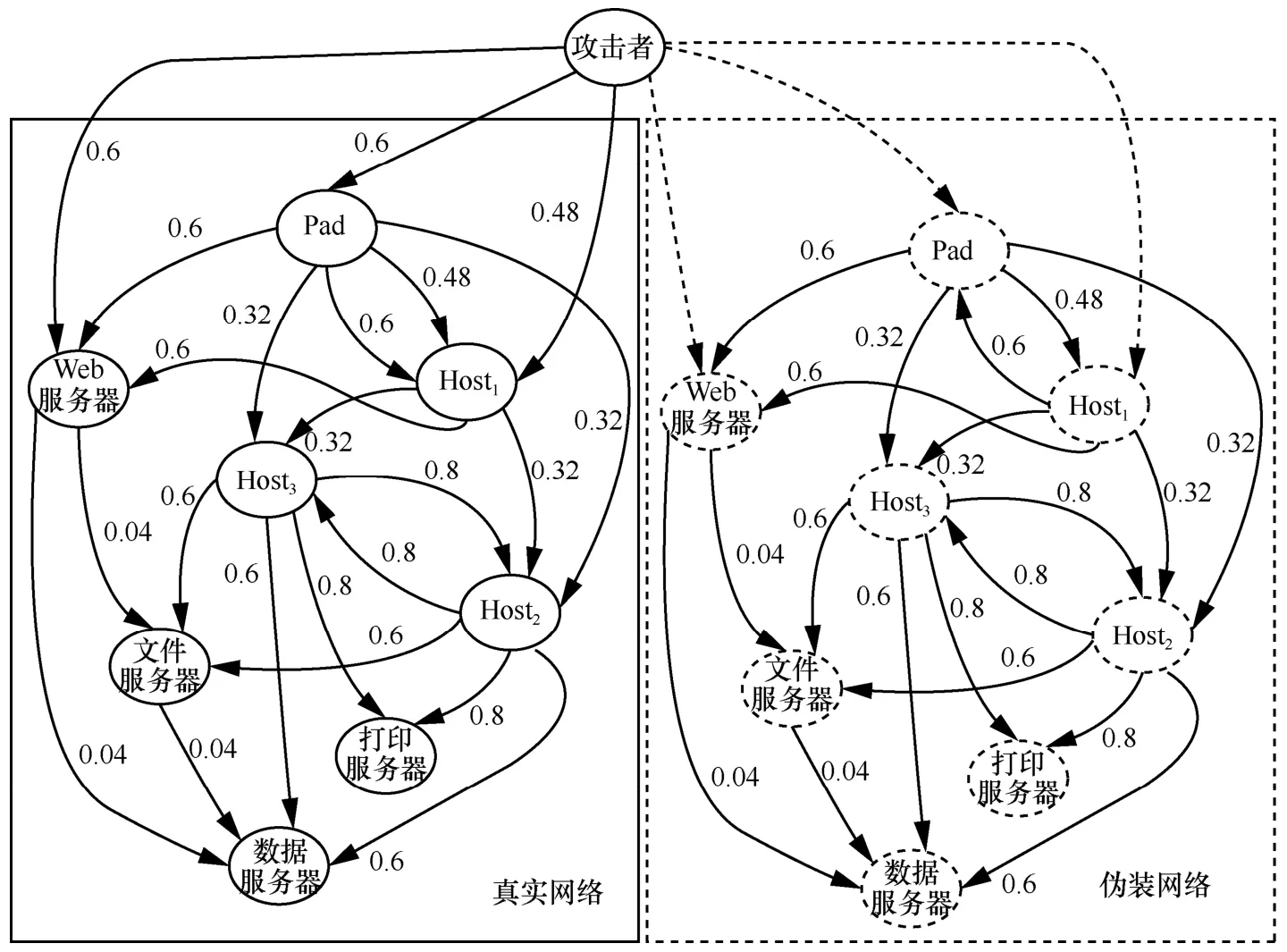
图6 实验网络的网络威胁渗透关系

由表4 可知，从文件服务器及打印服务器这2个节点对目标数据服务器进行渗透的难度较大，攻击者很少会对这2 个节点发起攻击。当攻击者由外部不断向网络内部渗透时，假设攻击者对防御者类型的信念p保持不变，攻击者需要花费的攻击代价c逐渐减小，存在精炼贝叶斯均衡EQ4。在此过程中，攻防双方均依据EQ4做出最优策略，防御者最优策略中的e1逐渐增大，表明随着攻击的不断深入，防御者发送真实信号的比重应该越来越大，而发送伪装信号的比重应该越来越小。

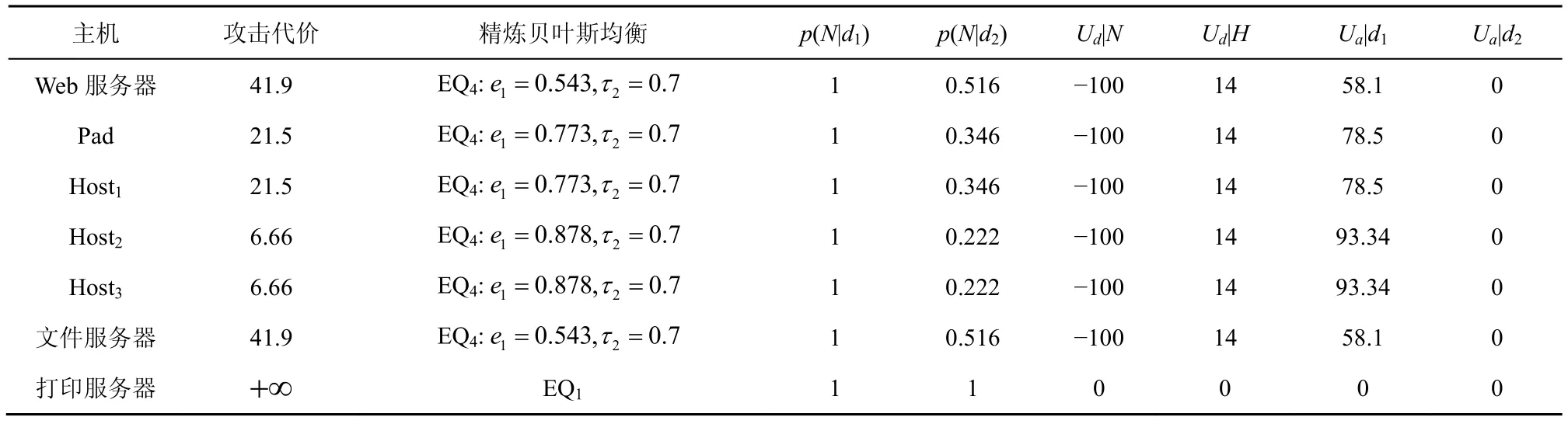
表4 攻击者处于网络中不同节点时的均衡分析结果

5.3 实验分析

通过分析精炼贝叶斯均衡的计算过程可知，攻击者对防御者类型的先验信念p和攻击代价c是影响策略选择和攻防双方收益的关键因素，且p和c可能会随着攻击者的渗透过程而变化。因此，本文进一步深入分析了p和c的变化对防御者最优策略的影响，其结果如图7 所示。由于在本文的信号博弈模型中，防御者首先做决策，即防御者具有“提前选择”优势，此种情况下攻击者只能在观测到防御者发出的信号后选择最优攻击策略，攻击者收益对多重均衡选择问题并没有影响，因此本文并没有关注p和c的变化对攻击者收益的影响。

在图7 中，当p和c同时变化时，攻防双方均依据精炼贝叶斯纳什均衡做出最优决策。图7(a)展示了当攻击者处于真实网络中（防御者类型为N）时，p和c的变化对防御者收益的影响。当时，防御者的收益保持在-30；当时，防御者的收益保持在-100；当时，防御者的收益与攻击者策略有关，保持在-100～-30 之间。图7(b)展示了当攻击者处于伪装网络中（防御者类型为H）时，p和c的变化对防御者收益的影响。当时，防御者的收益保持在 0；当时，防御者的收益保持在20；当时，防御者的收益与攻击者策略有关，保持在0～14之间。图7(c)展示了p和c的变化对防御者最优策略中参数e1的影响。当时，e1为0；当时，e1在0～1 之间。此外，由图7 可知，无论p和c如何变化，Ud|N＜Ud|H恒成立，故可知流量牵引能够提高防御者的收益。为了便于分析，进一步考虑了以下2 种攻防场景。

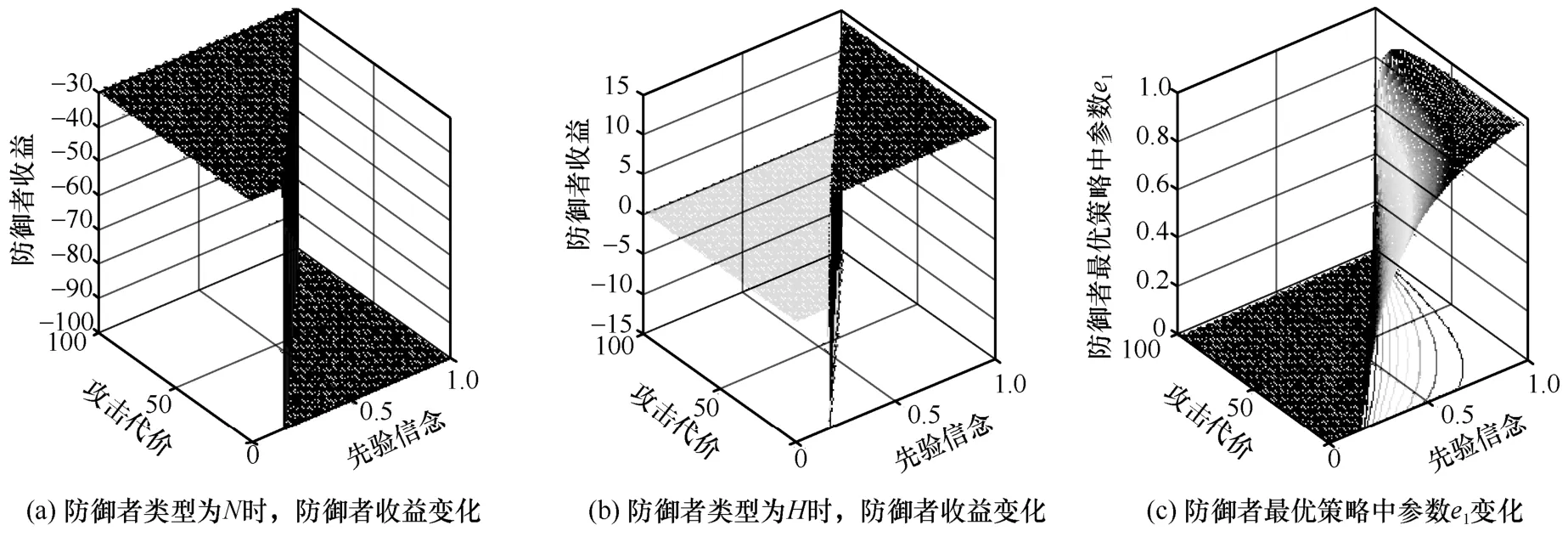
图7 先验信念p和攻击代价c的变化对防御者策略的影响

场景1攻击者对实验网络不断渗透，一方面攻击者对防御者类型的先验概率保持不变，另一方面由于攻击者位置与实验网络中漏洞情况变化会导致攻击者的攻击代价发生改变，即c变p不变。该场景中防御者策略结果如图8 所示。

由图8 可知，当攻击者处于真实网络中时，适当地提高c使其满足c＞p(g+k)-k，能够提高防御者的收益，本质上是提高攻击难度来震慑攻击者，使其不去攻击真实网络；当攻击者处于伪装网络中时，适当地降低c使其满足c＜p(g+k)-k，能够提高防御者的收益，本质上是降低攻击难度来诱惑攻击者，使其去攻击伪装网络以达到间接保护真实网络的目的。此外，当c＜p(g+k)-k时，若攻击者处于真实网络中，当c较大时，防御者策略中的e1较大，表明攻击者对虚假防御信号的分辨能力较差，此时防御者发送真实信号的比重应该越来越小，而发送伪装信号的比重应该越来越大，以最大化干扰攻击者。

场景2攻击者一直尝试从一个固定节点对目标发起攻击且实验网络的漏洞情况不发生改变，而攻击者对防御者类型的先验信念会不断变化，即p变c不变。该场景中防御者策略结果如图9 所示。

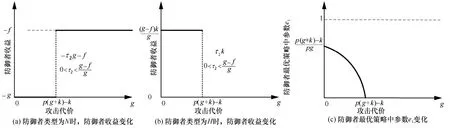
图8 c变p不变时对防御者策略的影响

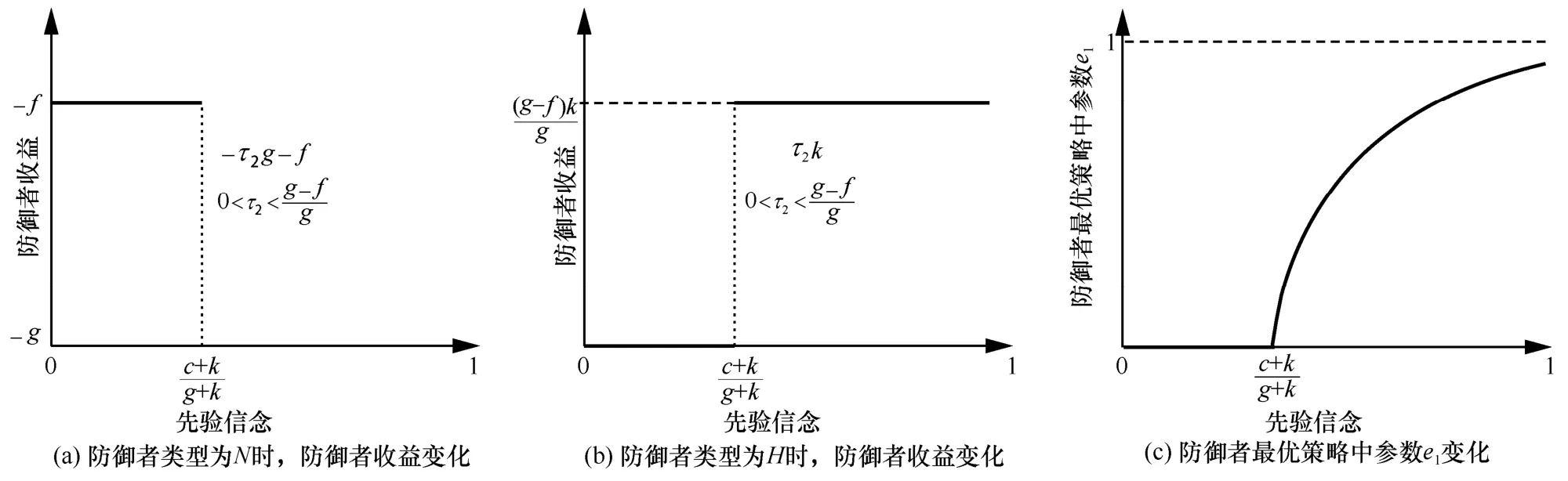
图9 p变c不变时对防御者策略的影响

由图9 可知，当攻击者处于真实网络中时，适当地减小p使其满足，能够提高防御者收益；当攻击者处于伪装网络中时，适当地增大p使其满足，能够提高防御者收益。该事实说明，防御者可利用社会工程学手段干扰并改变攻击者的先验概率来提高防御者收益。此外，当攻击者处于真实网络中时，随着其对虚假防御信号分辨能力的提高，p会不断变大，进而防御者策略中的e1变大，此时防御者发送真实信号的比重应该越来越大，而发送伪装信号的比重应该越来越小，防止防御信号被攻击者识别。

特别地，图8 和图9 中的垂直虚线表示均衡的一种特殊情况。在该均衡中，防御者收益受攻击者策略影响，为一变量。例如，图8(a)中，当c=p(g+k)-k时，均衡策略中攻击者策略参数范围为0<τ2<，对应的防御者收益为变量-τ2g-f。

信号博弈模型中，由于信号发送方能够混淆信号接收方对其类型的信念，使信号博弈模型在描述不完全信息的网络攻防中具有天然优势。当前，信号博弈模型已被很多学者应用于网络攻防策略选取上。鉴于此，将本文方法与其他典型方法对比，其结果如表5 所示。

表5 本文方法与其他典型方法对比

由表5 可知，文献[26,28-29]均不考虑混策略，仅有文献[27]和本文方法考虑了混策略，但文献[27]的博弈过程仅局限于单阶段且均衡求解方法不够详细，方法的通用性一般。本文方法适用于描述渗透攻击全过程，对场景描述详细，方法的通用性较强，且给出了一种详细的统一混策略和纯策略的均衡求解方法。均衡求解及防御策略选取也表明了混策略相比纯策略更适用于欺骗防御，能够增加策略对攻击者的干扰性，提高防御的实际效能。

综上可知，在基于伪装网络的网络主动欺骗防御攻防场景中，利用本文构建的信号博弈模型求解的精炼贝叶斯纳什均衡能够为防御者实施最优防御策略提供有效指导，实现防御者收益最大化。

6 结束语

为了抵抗目标性较强的渗透攻击，本文提出一种基于动态伪装网络的主动欺骗防御方法。借助动态伪装网络，防御者通过发送伪装信号来欺骗干扰攻击者。为了实现最大化防御者收益，将攻防过程用信号博弈模型进行刻画，进一步利用精炼贝叶斯纳什均衡解作为最优欺骗防御策略。所提方法能够同时求解出纯策略和混策略，且利用混策略更利于欺骗攻击者。实验结果表明，本文方法能有效欺骗攻击者，从而实现对真实网络的保护。未来的工作包括在动态伪装网络中利用MTD 技术加强对攻击者的干扰，并结合欺骗防御方法实现更有效的防御。