分时电价研究中采用持续负荷曲线洛桑德公式和概率倍加原理的探讨

张淑红，吴晋萍，张育全

（1.青岛工学院，山东 胶州 266300；2.国网太原供电公司，山西 太原 030012；3.山西大学电力工程系，山西 太原 030013）

0 引言

实施峰谷分时电价可缓解尖峰时段电力供需矛盾，提高系统负荷率，降低平均发电成本。国家监管部门规定：“峰谷时段划分要合理，原则上高峰时段不得超过低谷时段2 h；分时电价以电网平均电价为基础，高峰电价可为低谷电价的2～4倍。”[1]进入21世纪以来，电动汽车晚间充电日渐影响了地区日负荷曲线的形态，北方地区大规模的“煤改电”措施也影响了冬季的电力日负荷变化规律，城乡居民两段式“黑白电价”引导着晚高峰的电量向着白天低谷移动，诸多因素使峰谷电价这一节能举措面临着新的局面。2020年初，国家电网公司提出“电力需求响应工作两年行动计划（2020—2021）”，旨在发掘、发挥需求侧资源作用，扩大需求侧响应规模，催生多元化、规模化、市场化发展应用。因此，作为电力需求响应工作核心措施之一的峰谷电价必将再度引起人们的高度重视。围绕峰谷时段划分和峰、平、谷电价比两个核心问题，国内学者对此进行了长期研究，其中一部分学者着力于用户响应的研究。文献[2]根据峰电增收与谷电减收必须相等的基本要求，从用户响应视角出发，推导出反映峰谷分时电价结构的重要公式，对实施分时电价的行业反应做出了评价，认为电费支出占比及电价结构是影响分时电价响应的主要因素。文献[3]基于消费者心理学理论及加权最小二乘法，建立了分时电价下的用户响应模型及响应参数识别校正模型，解决了响应度曲线的斜率、死区拐点及饱和区拐点的获取问题；实例仿真研究表明，对用户响应度曲线不断进行修正，拟合出的负荷曲线更接近实测负荷曲线，这就为分时电价实施机构掌握用户的响应行为并制定合理的分时电价结构提供了科学依据。文献[4]以负荷曲线最大值、最小值为边界，构建了偏大和偏小型两种隶属度函数，采用尖、峰、平、谷4种定价模式，在分时电价模型中进行优化，选取削峰填谷效果最好、负荷曲线形状最优的模型即为时段划分的模型；而尖、峰、平、谷4个时段的电价是以该时段长期统计的累计平均市场结清价MCP（market clearing price）为基础制定的。文献[5]提出了用市场结清价MCP计算的平均购电价来确定平时段电价的方法，从一个可行途经将分时电价市场化，得到适应电力市场条件的分时电价体系。

本文基于地区年度典型日负荷曲线及其持续负荷曲线相关性，将长时段内峰负荷转移作为随机问题予以研究，提出了一种确定峰谷分时电价基本结构的新方法。

1 持续负荷曲线洛桑德公式

在特定时段内，不按时序而按负荷大小及其持续时间排列的派生曲线称为持续负荷曲线。20世纪20年代，德国学者就提出了持续负荷曲线指数型的解析公式，现被各国广泛采用的洛桑德（R ossander）公式有如下两种形式[6]

其中，β为持续负荷曲线最小负荷率，是测计期内最小负荷与最大负荷之比，即β=Pzx/Pzd；T为测计期，h；负荷变动指数1/λ为峰高与谷深之比，即1/λ=（1-f）/（f-β）；f为负荷率，

当1/λ<1.0，即f>（1+β）/2时，峰高<谷深，负荷变动较缓，用式（1）；当1/λ>1.0，即f<（1+β）/2，峰高>谷深，负荷变动剧烈，用式（2）。

负荷曲线及其参数与对应的持续负荷曲线如图1所示，持续负荷曲线是按同一负荷下持续时间的累加所得，即有t3=t1+t2。

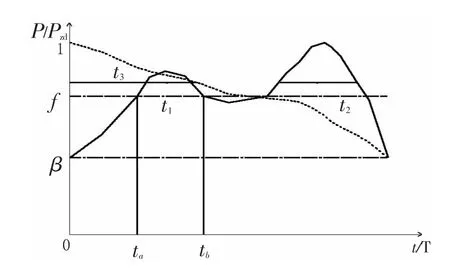
图1 负荷曲线参数与持续负荷曲线

图1中，Ppj/Pzd=f的水平线以上、负荷曲线以下面积之和即为尖峰电量，它与该水平线以上、持续负荷曲线以下面积所表示的电量是相同的，所以可以利用持续负荷曲线和洛桑德公式（1）或（2）来研究负荷曲线中尖峰电量向低谷转移的问题。

图1中ta-tb为早高峰时段，该时段电量由该区间的负荷曲线ab以下至坐标轴间的面积所表述，显然峰时段电量远大于同时段的尖峰电量。如果峰时段电价设计得过高，用户转移到低谷时段的电量会高于尖峰电量，严重时会造成系统负荷曲线峰谷倒置的情况，这将使电网企业面临巨大的经营风险；反之，用户原尖峰电量不大，而按远大于尖峰电量的峰段电量和较高的峰电价格付电费，加大了用户生产成本，电网企业则得到制度性的营业增收。故两种情况都应避免。

2 概率倍加原理在预测问题中的运用

计划评审管理技术是多工序大型工程或研究项目实施的管理手段。该项技术用三时点估计方法预测计划网络图中每项活动所需要的期望时间为

其中，a为最乐观时间；m为最可能时间；b为最悲观时间。

著名数学家华罗庚对期望时间计算作了如下的论证[7]：假定m的可能性分别是两倍于a、b的可能性，在a和m间的平均值是（a+2m）/3，同样，在b和m之间的平均值是（b+2m）/3，这2个平均值各以1/2的可能性出现的概率分布逼近实际的分布，这2个平均数的均值即为期望时间te，即te=1/2[（a+2m）/3+（b+2m）/3]=（a+4m+b）/6。从用户数量与时间变量双重因素考虑，对一个地区年内尖峰电量转移值进行预测是可以引用“概率倍加原理”的。

3 基于年负荷曲线预测的峰谷电价确定

3.1 峰平谷时段的确定

对当年前三季度地区供电负荷数据分析，考虑下一年各因素引起的电量变化，可以细致地预测下一年度指标和负荷曲线参数：年供电量、年线损率、最大负荷、最小负荷、基本电价水平下的年售电收入等，据此可建立与年售电负荷曲线相一致的典型日负荷曲线，选择对应的洛桑德公式（1）或（2），通过“用户响应”调查并参考过去掌握的数据，可初步确定用户响应后年度合计尖峰转移电量的最乐观值、最可能值、最悲观值，用反函数由这3个值可求得尖峰负荷转移时段的对应值ta、tm、tb；如绘出精细的年持续负荷曲线，可在年平均负荷水平线与持续负荷曲线构成的三角形中，从顶点往下量取表征3种转移电量值的面积，即可图解得到对应的ta、tm、tb值，两种方法所得结果可相互比较、修正；由式（3）求得尖峰转移电量期望值QP.e所对应的te，即为峰谷分时电价中要确定的尖峰时段期望值。

考虑到平时段是以平均负荷时点为中心且负荷变动幅度不大的区段，所以在持续负荷曲线上，以0.05Ppj为变动幅度，做2条Ppj的平行线，与持续负荷曲线2个交点j1和j2其对应的时点间隔即可定为平负荷时段；24 h减去平、峰时段之和即为谷时段值。诚然，时段值应取整数，还应满足高峰时段不得超过低谷时段2 h的基本要求。

3.2 峰平谷电价的确定

3.2.1 长时段峰谷电能量的确定

国内学者对持续负荷曲线P（t）及对应的线损曲线P2（t）采用概率倍加原理进行联动分析，得到长时段内最小、正常、最大方式3个区间的功率分点，解决了长时段线损预测的难题，也为确定峰谷分时电价结构时，峰、平、谷3者电量之比的预测提供了途径。文献[6]表格4-4中Px.zh、Pzh.d为谷、平、峰3个区段2个分割点功率值，现将该表格中属于高负荷率组合的数据转述如表1所示。

表1 谷、平、峰时段分点功值率

3.2.2 峰谷分时电价的确定

峰谷分时电价的设计遵循两项原则：总售电量不变；电网企业峰段增收与谷段减收相当。如记Q为电量，r为电价，下标p、s、v分别表示峰、平、谷，取平段电价为基本电价即rs=r，记峰谷电价比k1=rp/rv，峰谷时段电量比k2=Qp/Qv，峰平电价比k3=rp/rs，根据上述两项原则，经“用户响应”分析可得到分时电价结构公式

步骤1：按照监管部门要求，确定峰谷电价比k1，一般情况下均取k1=3.0。

步骤2：由年负荷曲线预测参数f、β，所得λ值，用插入法可从表1中求得3个区段功率分点值Px.zh、Pzh.d；用式（1）或（2）计算或用持续负荷曲线图解求峰谷时段电量比k2。

步骤3：将k1和k2代入式（4）即可求得k3，至此，峰谷电价结构已完全确定。

4 算例分析

浙江某地区典型日负荷数据如表2所示，预测下一年度年供电量581.64×108kW·h；预测年线损率为2.84%，按年基本电价水平预测年售电收入258.8×108元。

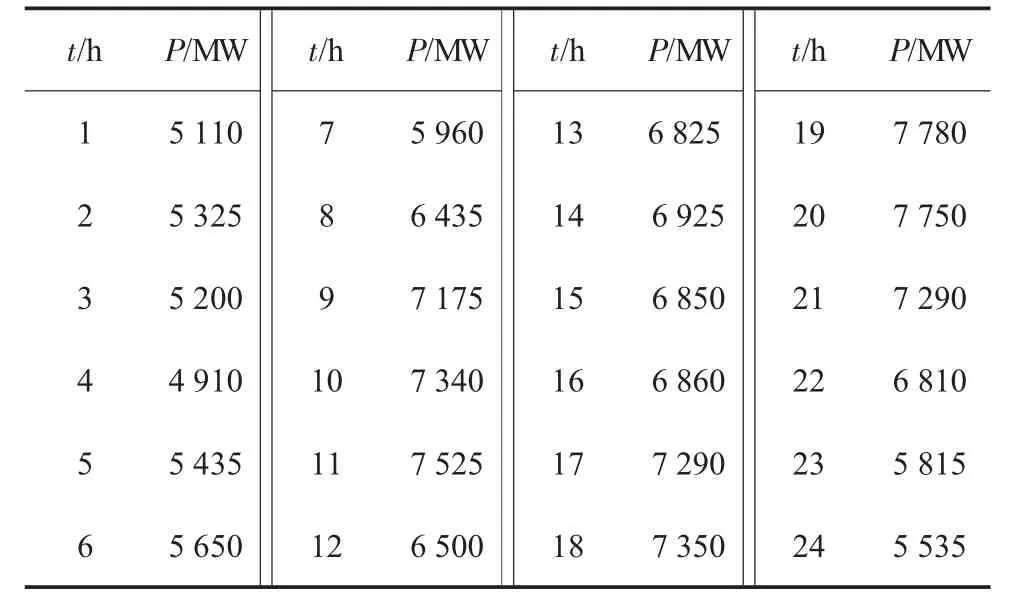
表2 典型日负荷曲线

4.1 时段分割计算

4.1.1 负荷曲线参数计算

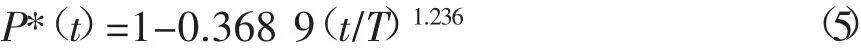
4.1.2 持续负荷曲线功率值的计算和作图

按式（5）算得各时点的功率值如表3所示，负荷曲线与持续负荷曲线如图2所示。

由图2可见，该持续负荷曲线近似以12点为中点的一条下降直线；在某一尖峰负荷下，持续负荷曲线下面积SA与该负荷下负荷曲线下面积SB与SC之和相等。

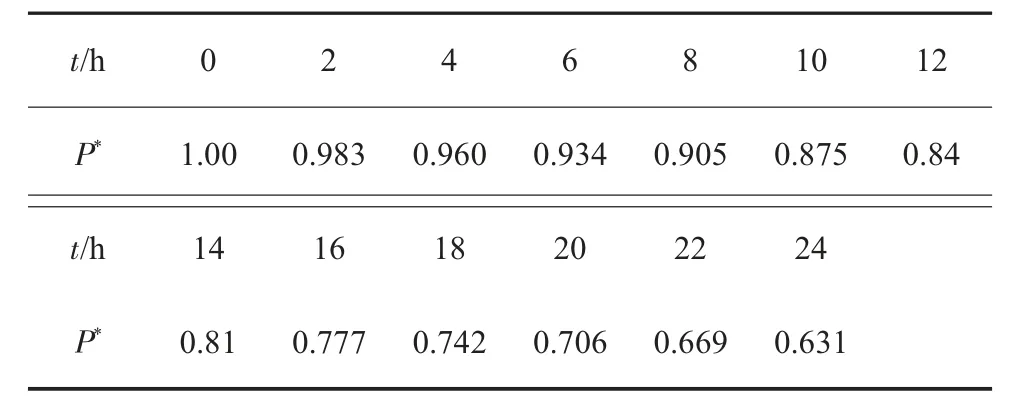
表3 持续负荷曲线功率标幺值

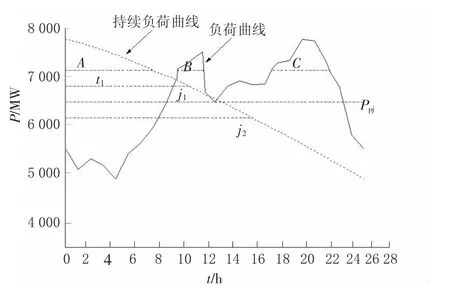
图2 某地区典型日负荷曲线与持续负荷曲线

4.1.3 图解求取峰段时间

因该持续负荷曲线近似为一直线，故转移电量占尖峰电量之比可由相似直角三角形面积之比来表述，而面积比与边长平方比关联，即其中，Qi为转移电量，QP为尖峰总电量；d为持续负荷曲线上半日的时长，即d=12 h。

设经大用户调查，最悲观、最可能、最乐观3种情况的（Qi/Qp）分别为0.20、0.35、0.55，由式（6）算得ta=5.36 h、tm=7.10 h、tb=8.90 h（下标a、m、b分别代表3种情况），将这代入式（3）即可求得尖峰转移电量的期望时间：te=（5.36+4×7.10+8.90）/6=7.11 h，取整数为7 h。这就是基于持续负荷曲线洛桑德公式和概率倍加原理求得的峰段时间。需要指出，按峰电量转移3种情况计算，峰电量转移期望值比例为36%，是较为合适的。

4.1.4 求取平段时间

设平负荷时段负荷变动幅度为0.05Ppj，作0.95Ppj（6 107 MW）和1.05Ppj（6 885 MW）2条平行线，与持续负荷曲线2个交点j1和j2，其对应的时间分别为10点和15点，该时距即为平负荷时段，为5 h，则谷负荷时段为24-（7+5）=12 h，满足峰负荷时段不大于谷负荷时段2 h的硬性要求。

4.2 峰、平、谷电价的确定

4.2.1 谷、平、峰段电量比的预测

设下一年的年负荷曲线特征与表2所示的典型日负荷曲线相同，已知λ=1.236，则1/λ=0.809 2，查表2可得P*x.zh=0.762 6，P*zh.d=0.928 1，各乘以最大负荷可得3个区段功率分点值：Px.zh=5 933 MW，Pzh.d=7 220 MW，按式（5）作指数运算，得功率分点时值tzh.d=6.4 h，tx.zh=16.8 h；按三角形加矩形面积求得谷、平、峰段日电量分别为39 035 MW·h、68 396 MW·h、48 000 MW·h，其比值为Qv/Qs/Qp=1.0/1.75/1.23；即得k2=1.23。

图解可得峰电量Qjf=8 345.7 MW·h，是峰段电量的17.4%；峰电量转移期望值则仅为峰段电量的6.26%，比例不大，可信度较高。

4.2.2 谷、平、峰电价的预测

由年供电量和线损率求得年售电量：Qsh=Qy（1-2.84%）=581.64×108×0.971 6=565.12×108kW·h，平段电价rs=总售电收入/总售电量=258.8×108/565.12×108=0.458元/（kW·h）。

如取峰谷电价比为常用值，即k1=3.0，由式（4）可得

代入k1、k2值可得峰平电价比：k3=rp/rs=1.426，则可得峰段电价rp=1.426×0.458元/（kW·h）=0.653元/（kW·h），最后算得谷段电价rv=rp/k1=0.653/3=0.218元/（kW·h）。至此，该电网企业下一年度的峰谷分时电价的基本结构设计所得结果是峰、平、谷3个时段分别为7 h、5 h、12 h；3种电价为0.653元/（kW·h）、0.458元/（kW·h）、0.218元/（kW·h）。

4.3 基本结构设计结果的校核

由3个时段电量按不同的单价计算，即可完成电网企业峰电增收与谷电减收相平、按基本电价水平计算的总收入不变2项校核。

本算例2项校核所得的误差为0.304%，原因是时段值取整和电量比值用了分析与图解综合的方法，但整个峰谷分时电价构成预测的结果是令人满意的。

5 结论与建议

本文所述的内容与算例表明，基于持续负荷曲线洛桑德公式和概率倍加原理确定峰谷分时电价构成的新方法，具有严密、简明特点，可以作为峰谷分时电价基本结构编制、分析和监管部门审核的参考。

近年来，有些地区电网已将峰、谷、平时段做了分割安排，这就是“用户响应”调查后的针对性措施。所以，本文提出的新方法可作为用户响应预测方法的比较与补充。

本文所述峰电转移量的悲观值、最可能值、乐观值和与用户响应理论中提出的用户响应度曲线的死区、比例区、饱和区相对应，探寻这种对应的概率本质，是需要利用用户负荷大数据和概率理论解决的新课题；电网企业所积累的不同季节的典型日大数据为精准预测下一年度售电负荷曲线参数提供了基础条件；建议专业和管理人员对上述两个问题进行探索，为不断提高峰谷分时电价确定过程的科学性而努力。