火炮回转支撑结构刚度特性研究

刘更喜，顾克秋，张新建

(南京理工大学 机械工程学院， 南京 210094)

回转支撑结构支撑火炮的回转部分，通过转动副实现火炮回转部分与下架之间的相对转动，是火炮结构的关键组成部分。火炮射击时，回转支撑结构传递来自上架的发射载荷到下架，使炮架保持平衡。良好的回转支撑结构对全炮稳定性以及总体性能有着至关重要的作用。

传统火炮回转支撑结构方案一般有两种，一种是立轴式，另一种是座圈式。立轴式回转支撑结构，通常设有立轴室，回转部分借助于方向机的作用，围绕立轴(基轴)在下架上回转以赋予火炮方向角，上下架断面之间留有一定的间隙，射击时，断面贴合在一起承受发射时的载荷[1]。为了使端面贴合在一起时不产生很大的冲击，端面的间隙必须保持很小，一般约为0.2～0.4 mm。由于回转部分的质心与立轴中心往往是不重合的，引起上下架端面之间的间隙前后不等，甚至会有局部接触。因此如何保持间隙均匀且在技术条件要求的范围内是此种结构方案的难点；座圈式回转支撑结构，采用封闭式单排或多排滚珠座圈连接上下架体，回转部分能够在圆周内自由平稳的回转，然而此方案缺点是座圈的质量较大，不利于火炮轻量化。

回转支撑结构是火炮的关键承力部件，在全炮静载或发射过程中，由于各个结构架体之间的复杂作用，其会受到轴向力、径向力、倾覆弯矩及突变载荷的作用，这些外载使得回转支撑结构发生变形，导致各连接部件之间载荷分配不均。因此，对于同时作为承载件和传动件的回转支承结构，进行刚度特性分析研究非常重要。

回转支撑结构也是作为全炮总体结构的子结构，起着重要的联接作用，在全炮动力学分析模型中，如何正确合理的构建结构刚度模型，如何准确地表征上下架之间连接的刚度特性，这对动力学分析模型和计算结果的准确性和可靠性有着很重要的影响。

现在国内外研究回转支撑刚度主要是两种方法：经典赫兹接触理论的刚度分析法、有限元数值分析法。1882年，赫兹发表了论文《论弹性固体的接触》[2]，有了著名的赫兹接触理论，赫兹接触理论在点接触问题上给出了一套完整的理论解，但是在线接触问题上，仅给出了部分理论解，也没有给出线接触弹性趋近量计算公式，所以还有待完善；Palmgren等[3]在大量实验数据统计的基础上，获得了线接触弹性趋近量经验公式，被广泛应用到现在的工程中。余海东等[4]对盾构机回转支承的刚度特性进行了研究，同时对各滚子沿周向分布的变形规律以及轴承受载变形的非线性关系进行了分析；黄东升[5]通过研究复杂系统有限元建模技术，对某轻型火炮座圈刚度进行了数学计算和有限元计算，并且借助轻型火炮平台，研究座圈刚度对射击稳定性的影响。彭迪[6]通对超轻型火炮结构动力学有限元分析的研究中也对立轴部分的刚度表征问题提出了解决方案。

本研究对某轻型火炮立轴回转支撑结构特性进行分析，同时运用刚度数值计算方法，采取有限元刚度分析手段，对其结构刚度特性进行分析研究，获得立轴回转支撑结构在全炮结构中刚度特性的表征方式。

1 回转支撑结构特性分析

1.1 一般立轴式回转支撑结构

上下架之间不同的连接方式对上架结构有很大影响，传统的火炮立轴式结构按照不同的上架结构类型通常分为长立轴式和短立轴式两种，短立轴式有称为带防翘板式[7]。

简单的长立轴式结构(见图1)，其前方两侧有固定高低齿弧的支座，支座上各有两个连接耳，用于固定上防盾，在连接耳的后方有耳轴室。上架的下部两侧有平衡机外筒，中间是上架的立轴，立轴上的轴颈与下架上立轴室相配合，下轴颈与下立轴室相配合。此种立轴结构较为简单，广泛应用于中、小口径火炮上。

长立轴式回转支撑的结构特点就是立轴较长且固定在上架或下架上，上架以及回转部分围绕长立轴旋转，同时通过长立轴把载荷传递到下架，而且长立轴由于其结构特点可以抵抗弯矩。

图1 长立轴式结构上架示意图

短立轴式结构(见图2)通常应用与大口径火炮上，在长立轴下面加止推轴承和蝶形弹簧以支撑回转部分，并使上下架断面之间留有一定的间隙。由于大口径火炮回转部分较重，回转摩擦力矩较大，且质心离基轴(短立轴)较远，为了使基轴处不上翘，通常在上下架端面之间回转部分质心之前添加滚轮结构。此种立轴式结构的特点就是立轴很短，不能抵抗弯矩，上架前端较长并由一个防翘板与下架连接。

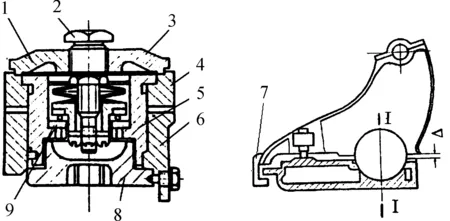
1-立轴盖板；2-调整螺钉；3-蝶形弹簧；4-上架；5-立轴；6-下架；7-防翘板；8-螺帽；9-滚珠轴承

图2 短立轴式结构上架示意图

1.2 本研究中的立轴回转支撑结构

在全炮结构中，回转支撑结构部分上与上架底板固连，下与下架之间通过立轴连接，结构简图如图3所示。立轴回转支撑结构主要由上架底板、立轴结构、下架、滚柱导轨4部分组成，上架底板2与下部架体1上表面之间设有滚柱导轨4，与立轴结构1配合工作使得火炮回转部分能够在下部架体上平稳回转，同时承受发射载荷。

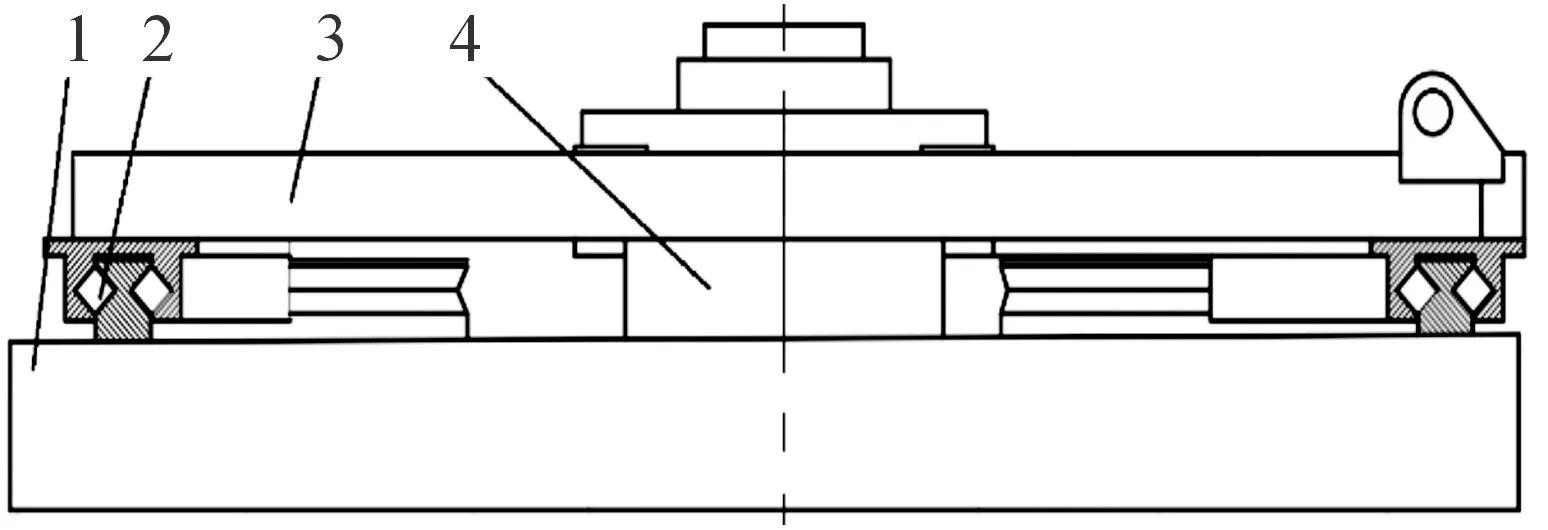
1-下部架体； 2-滚柱导轨； 3-上架底板； 4-立轴结构

如图3中的滚柱导轨所示，滚珠导轨部分作用类似交叉滚子轴承，其在静载状态下，全炮质心偏离导轨几何中心线较远，因此滚柱导轨在非发射状态下和调炮过程中主要承受轴向载荷以及倾覆载荷。在全炮动力学建模分析中，此部分结构包含大量的接触对，连接关系复杂，直接建模计算时间成本较大。本研究把此部分结构从全炮模型中独立出来，建立滚珠导轨刚度有限元模型，分析其刚度特性。

立轴结构(见图4)主要由立轴1、立轴盖板2、上轴承3、下轴承4以及立轴室5组成，是整个回转支撑部分结构以及全炮回转的基础，立轴通过立轴盖板与上架底板固连，同时立轴与上轴承3和下轴承4的内圈紧固在一起，与上架底板以及上架一起构成回转部分，在调炮时，整个回转部分结构以立轴轴线为旋转中心线，作往复旋转运动。轴承外圈与立轴室5固连，同时立轴室与下部架体连接在一起，作为整个火炮的回转基座。

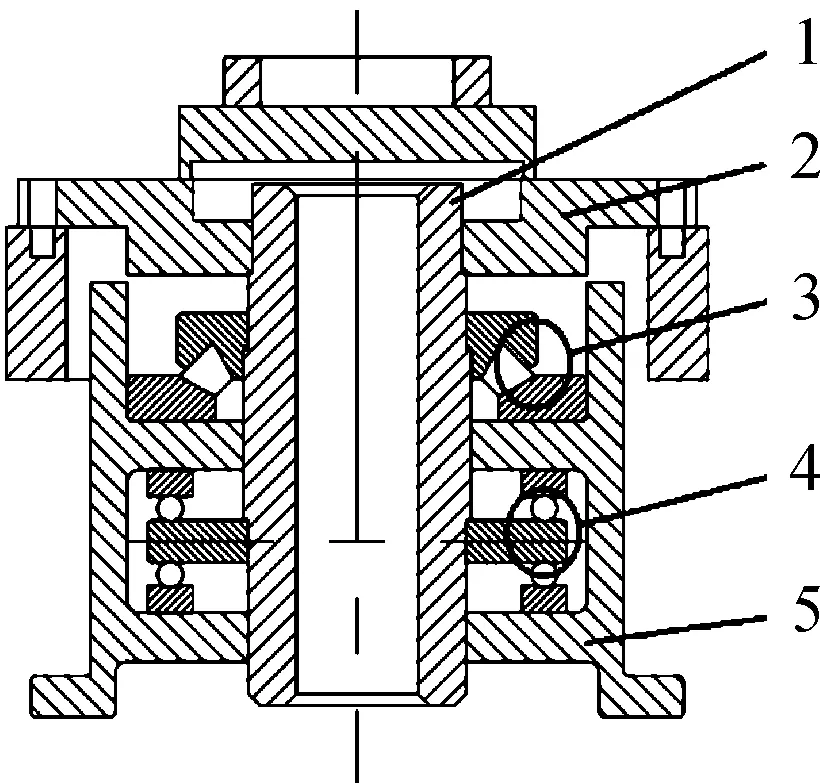
图4 立轴结构简图

立轴结构部分的刚度主要由上下两个轴承来决定，上轴承是推力调心滚子轴承，可以承受轴向载荷和径向载荷、下轴承为推力球轴承，主要承受轴向载荷，不能承受径向载荷，上下两个轴承配合工作形成组合轴承。立轴结构轴向刚度由上下轴承刚度耦合而来，径向刚度主要由推力调心滚子轴承单独构成。

2 回转支撑结构刚度特性分析

上节对回转支撑结构进行了结构特性分析，对其内部结构特点、工作方式、以及承载环境有了清晰的认识。本节将对如何在具体的刚度特性分析当中表征结构的刚度，以及如何在全炮动力学建模中处理支撑结构的刚度特性，作具体研究。

2.1 回转支撑结构刚度特性表征策略

根据立轴回转支撑结构在全炮当中的位置及工作特点可知，其主要位于上架底板与下部架体之间，同时承担传动和连接的作用。如图5所示，分别把滚柱导轨结构和立轴结构采取两个刚度连接单元来表征其在全炮中的连接关系。

滚柱导轨结构主要是由滚柱和导轨组成，上下导轨分别与上架底板和下部架体固连在一起，上下导轨之间通过建立刚度连接单元来模拟上下导轨之间的轴向刚度、径向刚度。

立轴导轨结构主要由上轴承和下轴承组成，上下轴承的内圈同时连接在立轴上。在立轴刚度计算模型中，可以将立轴轴承支撑系统分为三个部分：上轴承刚度、下轴承刚度、轴承座刚度，轴承支撑的刚度是由这三部分耦合计算求得，而在在实际轴承支撑刚度计算中，轴承座具体建模不在刚度计算当中，因此仅考虑剩下两者的耦合计算，轴承耦合刚度则根据弹簧串并联系统的刚度计算方法来计算。

立轴结构轴承等效刚度：

(1)

式中：k12为轴承等效刚度；k1为上轴承刚度；k2为下轴承刚度。

根据上述公式，求得k1、k2即可获得轴承支承的等效刚度值，后续章节则运用有限元数值解法分别计算刚度参数。

图5 回转支撑结构刚度逻辑框图

2.2 滚柱导轨刚度分析计算

对于传统赫兹接触理论解析方法来说，其假定套圈近似为刚体，除局部接触变形外无偏离初始几何形状的整体变形，忽略了套圈形状变化对接触状况的影响；而实际情况并非如此，因此计算出的座圈刚度与实际刚度有一定差距，而使用有限元法可以综合考虑上述因素的影响，计算结果更加精确可靠。本章分别使用理论法和有限元法研究计算不同载荷下的刚度，并进行对比分析。

2.2.1赫兹接触刚度理论

赫兹接触理论基于以下假设：① 材料是均质的；② 接触区的尺寸远小于物体的尺寸；③ 作用力与接触面垂直(即无摩擦)；④变形发生在弹性极限内。

图6为赫兹线接触示意图。对于线接触情况，赫兹给出了部分理论解：

(2)

式中：b为接触面半宽；ρ1、ρ2为两接触体截面曲率半径；E1、E2为两接触体材料的弹性模量；μ1、μ2为两接触体材料的泊松比；P为总法向载荷；L为接触长度。

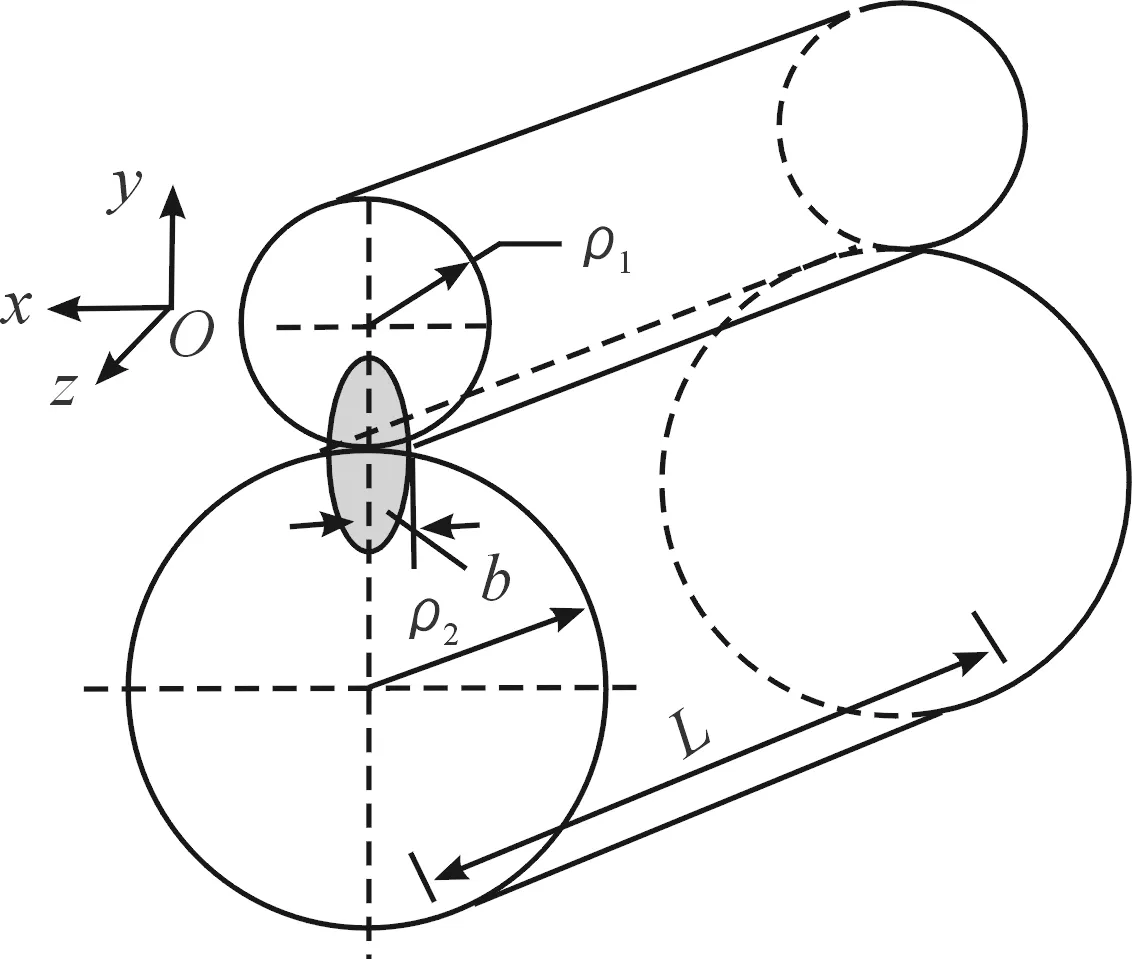
图6 赫兹线接触示意图

赫兹并没有给出弹性趋近量的求解方法。

一般光滑弹性体接触理论中的法向接触变形公式如下：

δ=ηbp0K

(3)

其中：K为第一类全椭圆积分；p0为最大接触压力。η的求解表达式为

(4)

国内学者丁长安[8]等根据式(3)推导出有限长线接触下的弹性变形公式如下：

(5)

对于面——面接触的非线性问题[9]，比如推力球轴承的接触问题，图7表示滚动体与轴承座圈接触情况，根据赫兹理论，滚动体与滚道在载荷的作用下接触时，产生的压力面应是椭圆形。对于弹性模量E=2.08×105N/mm2及泊松比为0.3的轴承钢，根据赫兹理论可推出滚动轴承接触变形的弹性趋近量公式如下：

(6)

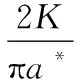
图7 滚动体与轴承座圈接触示意图

2.2.2有限元模型

1) 基本假设和模型简化

为简化建模现作如下假设：

① 上下导轨与滚柱接触表面皆为刚性，不发生变形。

② 下导轨静止，上导轨随载荷产生位移。

③ 滚珠导轨结构主要由上导轨、下导轨和滚子组成，建模时作适当简化：忽略倒角、边棱；忽略保持架的影响；忽略径向与轴向间隙的影响；将导轨几何中心的相对位移量近似作为刚度变形量计算，与其相对应的是轴承整体刚度。

2) 网格划分和边界条件

为了保证接触计算精度，采用三维六面体实体单元对几何模型进行有限元网格划分。单元类型采用线性缩减积分单元，以减少计算工作量。

对滚子与滚道之间的相互接触碰撞作用关系，可通过在滚子与上下滚道之间可能发生接触的表面区域定义面对面的接触对模拟，并采用“硬接触”作为接触对的法向接触属性。图8为滚子与上下滚道之间接触的示意图。

边界条件定义为对下导轨底面施加固定约束，在上导轨中心建立参考点并与上导轨建立耦合约束，对耦合点施加轴向和径向载荷，计算相应的变形量，求得滚珠导轨的轴向与径向刚度。

图8 滚子滚道接触示意图

2.3 计算结果与分析

1) 滚柱导轨结构刚度分析

将滚柱导轨几何参数代入本文2.2节相应的公式，计算出刚度的经典赫兹解，并与有限元结果进行对比，讨论有限元刚度解的正确性与可靠性，由于滚柱导轨的结构特点，其轴向刚度是问题分析的重点，因此本研究主要验证轴向刚度有限元解的准确性与可靠性。表1、表2分别为轴向刚度有限元解和轴向刚度赫兹解，图9为有限解刚度值和赫兹解刚度值的分析曲线。

由表1、表2和图9可以看出，滚柱导轨轴向刚度呈非线性，刚度随着载荷的增大而增大，但是增加趋势越来越平缓。有限元求出的刚度与赫兹理论求出的刚度有差别，这是因为赫兹理论在分析时作了许多假设，忽略了一些变形，而有限元法计算时考虑了这些变形因素，所以导致计算出的刚度比赫兹理论求出的刚度小。随着载荷的增大，赫兹解与有限元解两者之间的差值越来越小，这是因为随着载荷的增大，忽略的那些变形相对于整个变形所占比重越来越小，两个计算结果越来越接近。

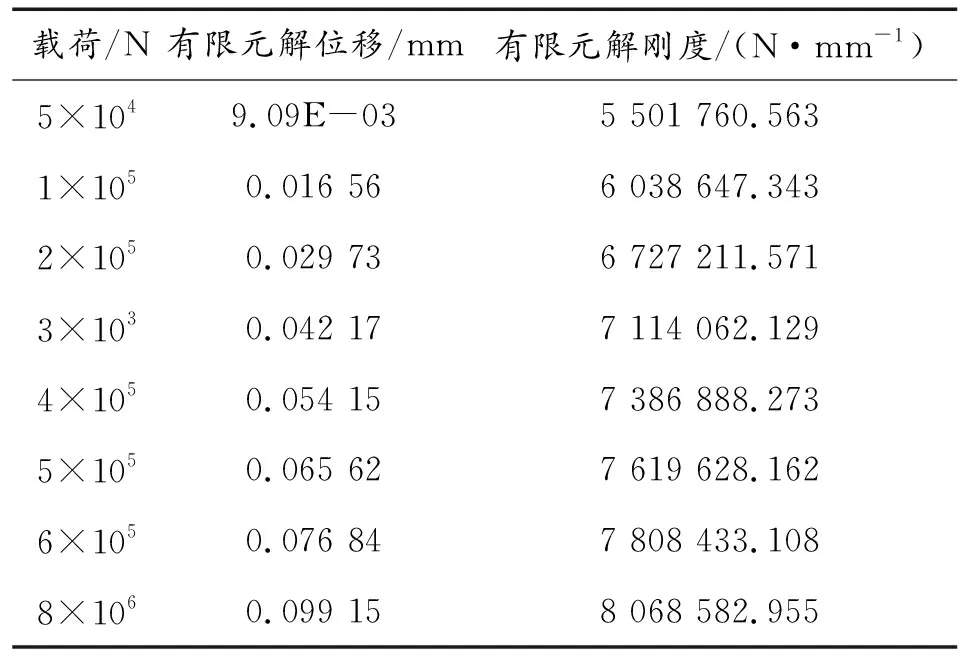
表1 刚度有限元解

表2 刚度赫兹解

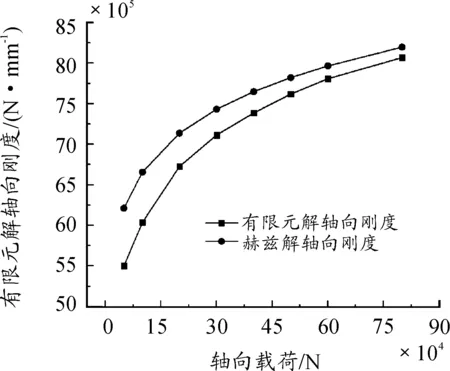
图9 刚度分析曲线

2) 立轴结构刚度分析

立轴结构主要由推力调心滚子轴承和双向推力球轴承上下两个轴承组成，本节对两个轴承分别独立建立刚度有限元模型，计算其刚度。

双向推力球轴承由上、中、下三座圈、保持架和球体构成，用于承受轴向载荷。推力调心滚子轴承由上下座圈、保持架和球体构成，用于承受轴向和径向载荷。本研究首先对轴承结构进行三维实体建模，然后对其进行有限元静力接触分析，为立轴结构刚度的计算分析提供数据支撑。轴承有限元模型如图10和图11所示。

图10 下轴承有限元模型 图11 上轴承有限元模型

施加载荷对下轴承刚度有限元模型进行求解，对轴承的弹性趋近量的赫兹理论解与有限元分析结果如表3所示。

表3 轴向变形结果

对上轴承刚度有限元模型进行求解，分别施加轴向载荷和径向载荷，对轴承的弹性趋近量的赫兹理论解与有限元分析结果进行对比，如表4、表5所示。

表4 轴向变形结果

由表3～表5可以看出，有限元分析结果与赫兹理论解比较接近，因网格划分、穿透等原因造成的误差在可接受范围内，所以可以认为对轴承接触问题的有限元分析结果是可靠的。计算得到下轴承刚度为2.99×106N/mm，上轴承有限元解轴向和径向刚度为2.13×106N/mm、5.12×106N/mm。

3 结论

通过对火炮立轴回转支撑结构工作原理、结构特性以及刚度特性分析研究，得到在全炮动力学分析中的结构刚度特性分析建模策略。建立了有限元刚度计算模型，得到该滚柱导轨结构整体刚度及变形分布以及立轴结构轴承刚度计算结果，该结果合理有效。本文的分析研究为火炮立轴回转支撑结构刚度特性的表征问题提供了有效解决方案，可为火炮立轴结构方面的研究提供了重要参考。