爆炸冲击下某车辆底部梁结构设计优化

胡建宇，王显会，周云波，张 明，孙晓旺，李高伟

(南京理工大学， 南京 210094)

车身抗爆炸冲击能力是装甲车辆的关键防护性能之一，它是车辆抵御爆炸物产生的冲击波对车辆结构和车内乘员损伤的能力[1]。在地雷的爆炸冲击作用下，车辆底部最易受损，轻则可能使汽车失去行驶能力，重则威胁驾驶员和乘员的人身安全，所以对装甲车辆底部实施防护措施是必不可少的[2]。目前，ALE算法既能够有效的跟踪物质结构边界的运动，又能让网格可以根据定义的参数在求解过程中适当调整位置，使得网格不致出现严重的畸变，从而国内外基本利用ALE流固耦合[3-4]的方法对车辆进行抗爆炸冲击的模拟仿真。Zakrisson B等[5]采用该方法模拟了空气场中近场爆炸冲击载荷作用下的结构变形; Fatt等[6]模拟了三明治结构对车辆防护能力的影响；石少卿等[7]和王显会等[8]分别研究了钢板-泡沫铝-钢板新型复合结构和蜂窝夹层结构抗爆炸冲击波能力，仿真与试验结果基本一致。然而在全尺寸的车辆仿真中，车辆有限元模型单元总数多于百万，计算成本高，所以目前对于大模型仿真优化问题，国内外已经开始基于实验设计、响应面法的多参数优化方法(MO)解决该类问题。Ran W等[4]提出了基于因子分析的多参数优化(FAMO)，以降低提高车辆抗爆性能的计算成本；Shariyat M[9]采用基于DOE的响应面方法(RSM)来最小化发动机引起的不平顺性。

本文基于有限元软件LSDYNA中的ALE流固耦合的算法对某军用装甲车辆进行仿真分析，评估其防护能力，随后进一步对比三种梁结构对车辆底部防护能力的影响。选择防护性能最优的梁结构，通过采用多目标遗传算法(MOGA)对其进行优化设计，得到最优解后再通过仿真验证其准确性。

1 原车建模及防护能力分析

1.1 原车有限元建模

目标车型没有进行过防护性能试验，因此模型建立的准确性直接决定仿真分析准确性和防护方案设计的可行性。保证模型建立准确性的方法为对原车进行模块化管理，即准确建立各个模块，模块化管理可方便根据分析结果修正仿真模型，大量分析和模型调整之后可保证模型的整洁性和准确性。

由于整车包含许多复杂的零部件，所以要对整车模型进行简化；对原数模中部分构件之间干涉穿透的现象进行修复；去掉模型中多余的特征点、合并自由边[10]。

对整车数模中车身的每个构件进行的网格划分，单元网格类型为四边形单元和三角形单元，其中三角形单元所占比重小于10%，网格单元尺寸为10～20 mm。车身底甲板是仿真分析的主要部件，采用10～15 mm的单元尺寸进行划分。网格划分从形状较小且复杂的曲面开始，所有构件网格划分完毕后要检查网格质量，检查的项目包括最小边(大于5 mm)、翘曲度(小于15°)、最大/最小角度(大于45°小于135°)、单元的雅克比(大于0.65)等[11]。模型单元总数为 2 159 919，节点总数为 2 000 055，原车主要材料技术参数如表1所示。

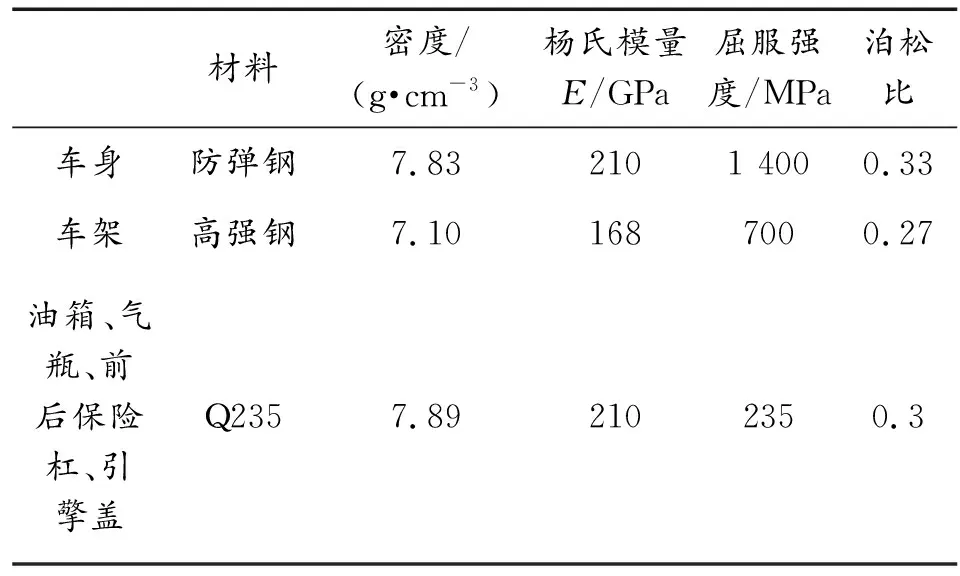
表1 原车主要材料技术参数

1.2 原车防护能力分析

在6 kg地雷当量下，对车辆进行底部爆炸仿真分析，根据车身底甲板响应结果，评判其防护能力。在车身底甲板受爆炸冲击作用下，考察其Z向最大塑性变形量，考虑底甲板向上变形所引起的结构碰撞，制定车身防护结构底甲板变形的设计要求，即最大塑性变形量，以此目标加强车身底部的防护性能。

爆炸仿真模拟中，为确保仿真模拟的准确性，按照建模规范，建立有限元模型如图1。空气网格模型(图中最大的长方形部分)能够容纳车身底部。空气单元尺寸的选择按规定大约是车身单元的2倍。土壤网格模型(图中最下面的长方形部分)，上表面与空气网格模型的下表面采用共节点的方式实现连接，6 kg当量的TNT地雷放置在车身底部中心正下方，浅埋地下100 mm，TNT地雷包含在土壤内部，引爆点位置不能低于炸药的1/3高度位置。

图1 有限元模型件示意图

基于ALE流固耦合的算法来模拟地雷引爆所产生的冲击波在土壤和空气中传播过程以及冲击波对车体的响应。耦合方式采用的是针对壳单元的罚函数法，仿真中空气模型与车身结构模型网格单元的尺寸关系(流体为固体的2倍)，流体端面积分点为2、罚函数刚度缩放因子为0.2、耦合时单元中流体体积最小百分比为0.5、摩擦因数为默认值[11]。对整车全部构件设置自接触，以避免各个构件之间在爆炸冲击波的推动下产生干涉，确保仿真的真实性。

基于LS-DYNA计算30 ms，输出底甲板位移曲线如图2所示，底甲板最大变形量为159 mm。

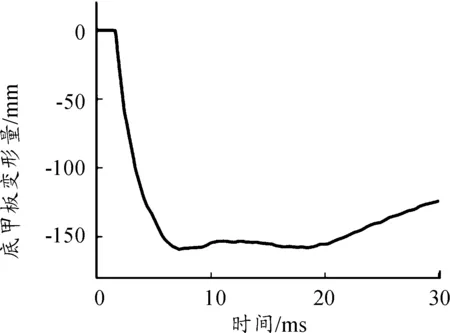
图2 底甲板位移曲线

输出底甲板内能和动能曲线，如图3、图4所示，在车辆底部受到爆炸冲击后2.7 ms，底甲板内能到达峰值17.9 kJ，随后内能开始下降，最后稳定在12.1 kJ；在车辆底部受到爆炸冲击后2 ms，底甲板动能到达峰值35.2 kJ，随后逐渐衰减至0。

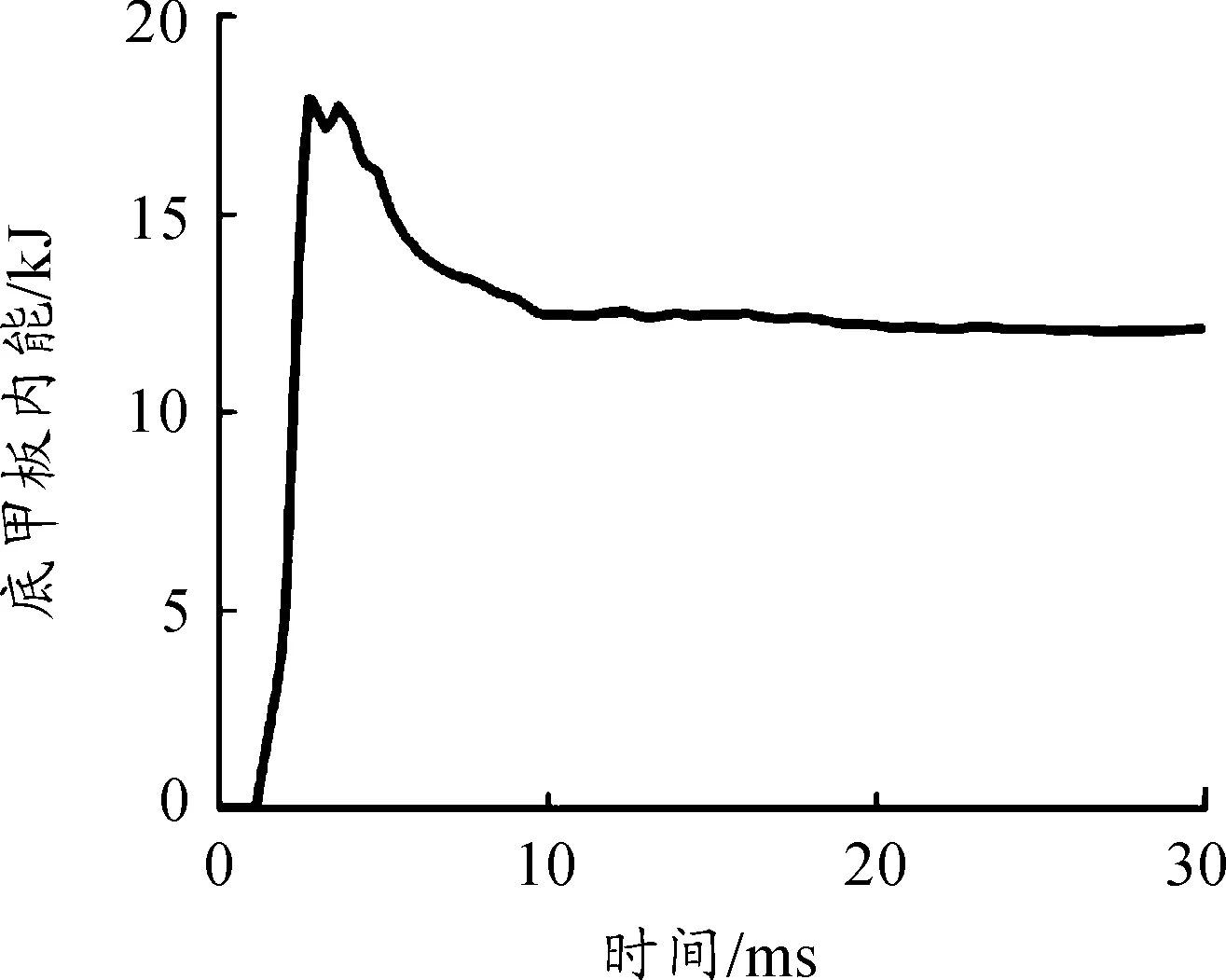
图3 底甲板内能曲线

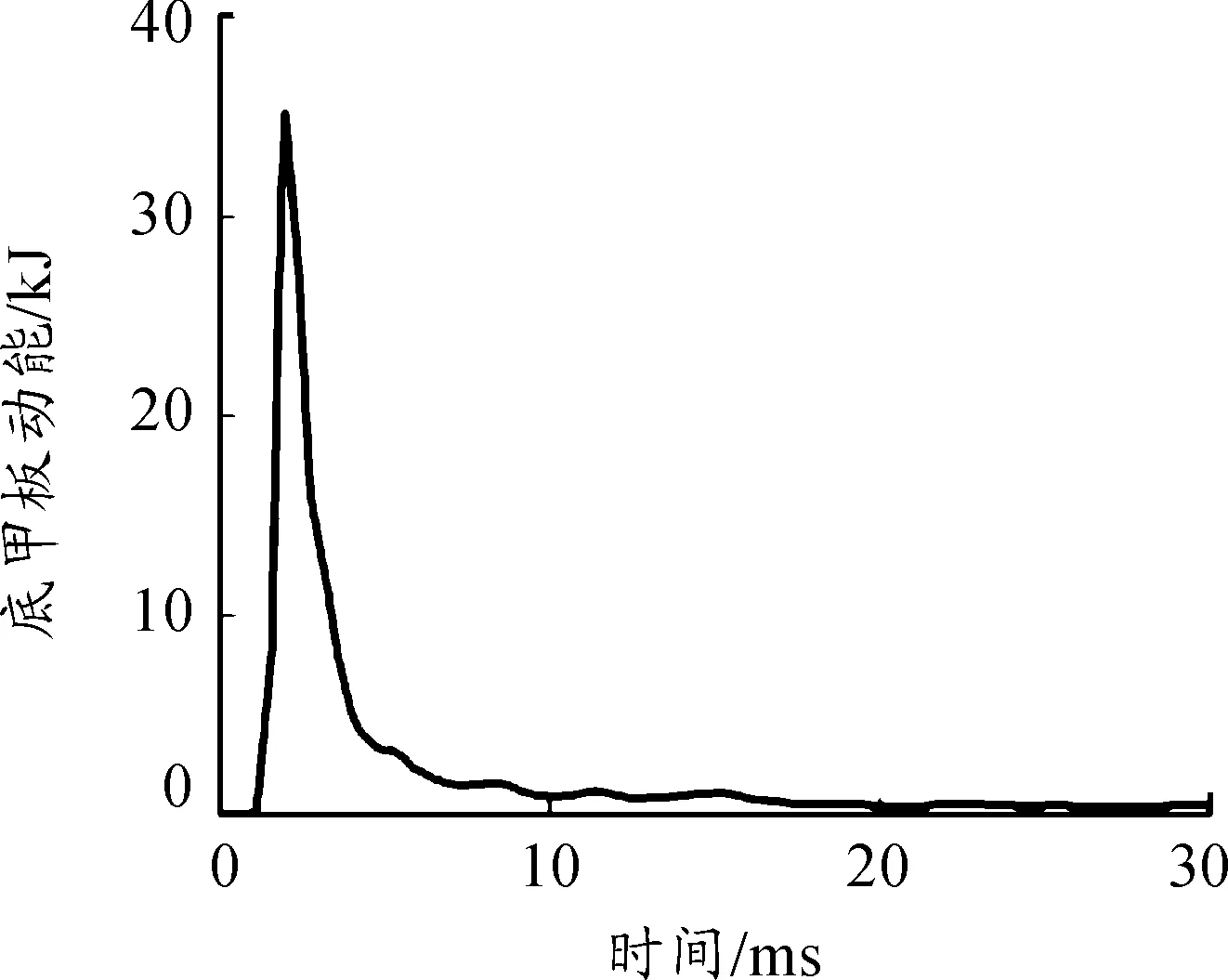
图4 底甲板动能曲线

输出底甲板合应力云图，如图5所示。应力主要集中在底甲板前半段，应力在底甲板前端四分之一处两侧达到最大，最大值为2 046 MPa。

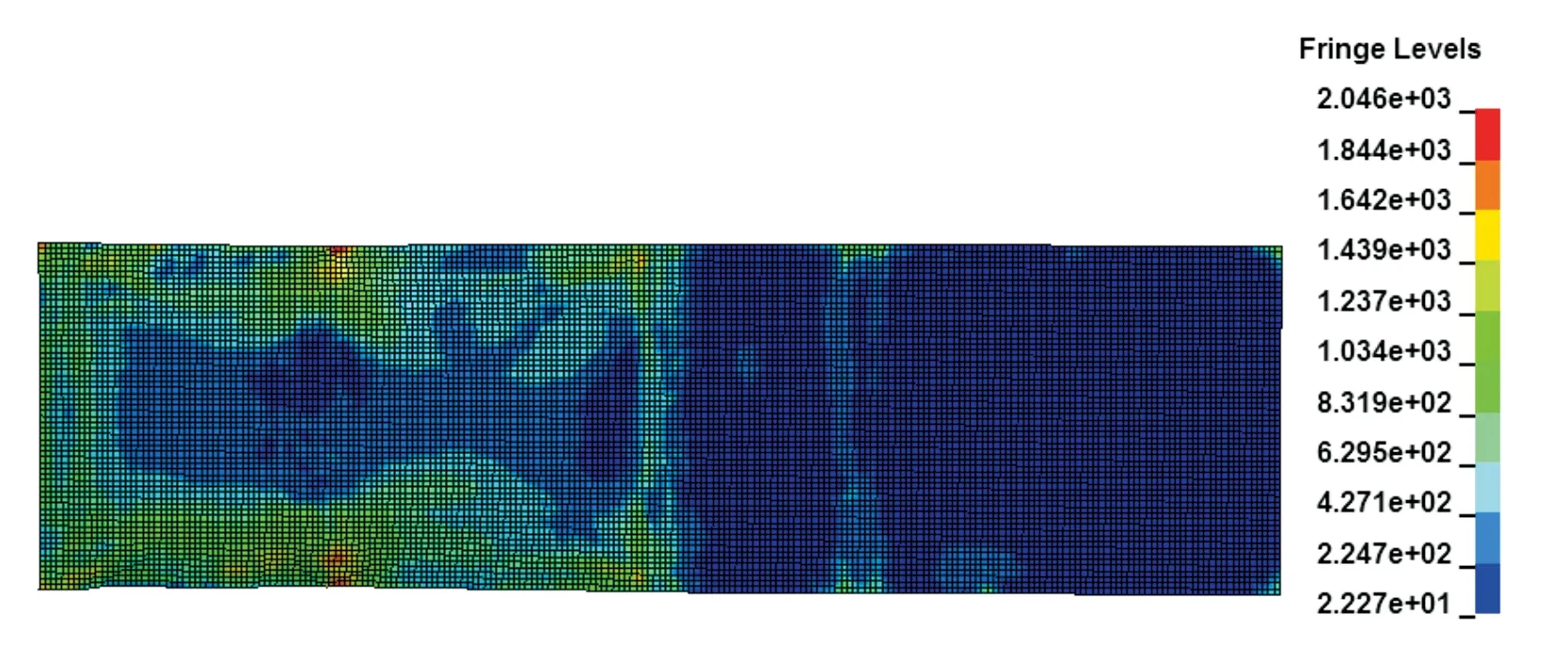
图5 底甲板合应力云图

底甲板最大变形量为159 mm，远超过底甲板与地板之间的距离110 mm，而底甲板与地板产生碰撞必然会导致车内乘员受到严重损伤。原车底部地板，中部为平板，两侧为对开的V形板，V形结构有利于将能量分散到车身两侧，但是中部平板无加强梁结构，两侧斜板外侧梁结构较弱，这会导致车身底部结构刚度不足，不利于能量的分散，所以必须通过在底甲板上方增添梁结构来增加车辆底部结构刚度，即减少底甲板的最大变形量，降低底甲板应力，从而减少车内乘员的损伤。

2 三种梁结构防护能力对比分析

梁是车辆防护结构中常用的部件，主要用来支撑板和承受板传来的各种竖向载荷，从而提高整体的刚度，起到抗震、抗裂、稳定等构造性作用。梁按照截面形式，可分为：矩形截面梁、T形截面梁、工字形截面梁、口形截面梁、几字形截面梁及不规则截面梁等等。本文选取工字形截面梁、口形截面梁和几字形截面梁进行仿真计算，从而对比三种梁防护性能的优劣。

2.1 三种梁结构模型建立

三种梁的布置形式相同，均为在底甲板上方均匀布置四根梁，形状与底甲板相适应，如图6所示。3种梁的材料均采用高强钢，其材料参数见表2，梁厚度为10 mm，高度为80 mm，上表面宽度为50 mm，采用BEAM模拟梁与底甲板之间的焊缝。

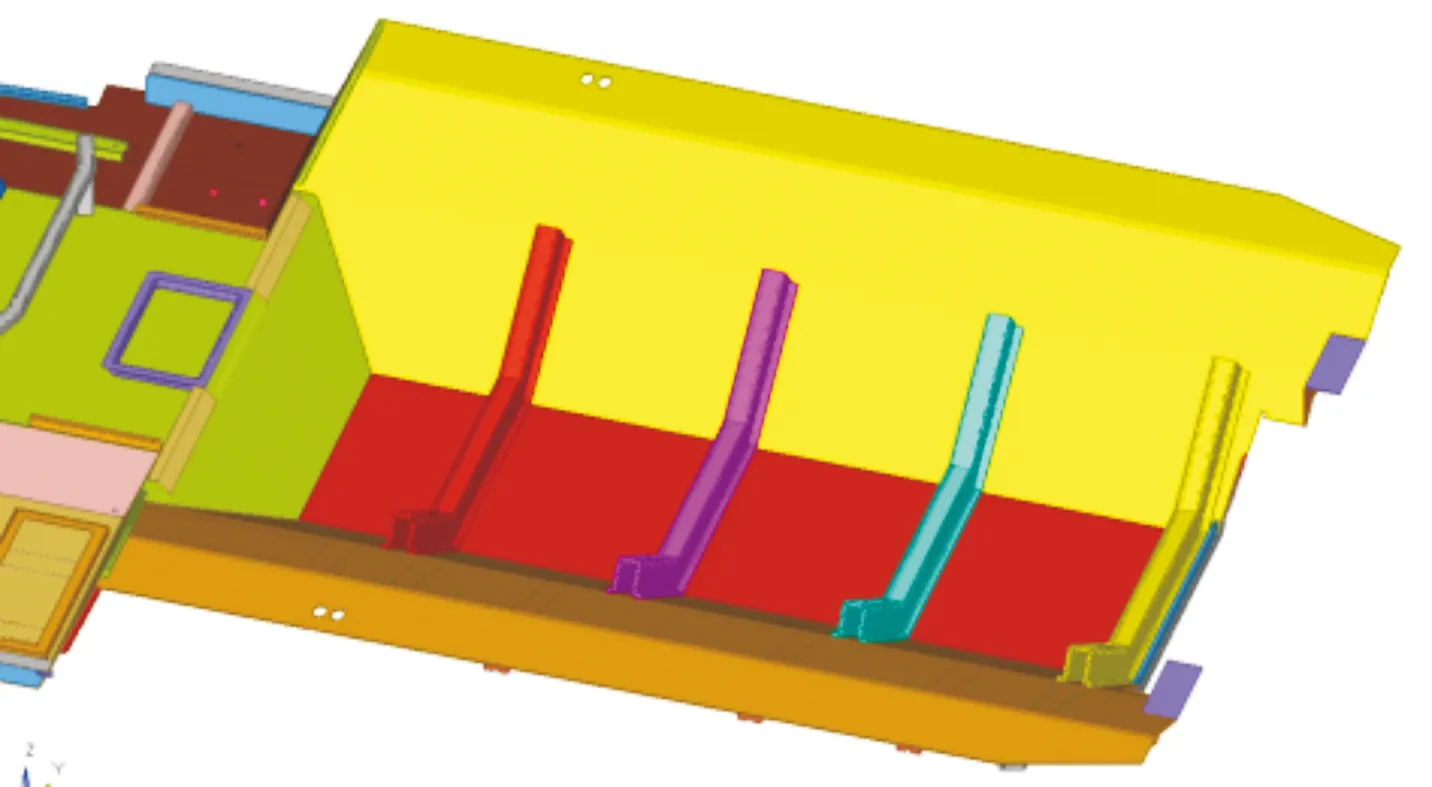
图6 梁布置示意图

表2 高强钢的材料参数

4根几字梁重106.7kg，工字梁重77.13kg，口形梁重111.2 kg，3种梁模型截面如图7所示。

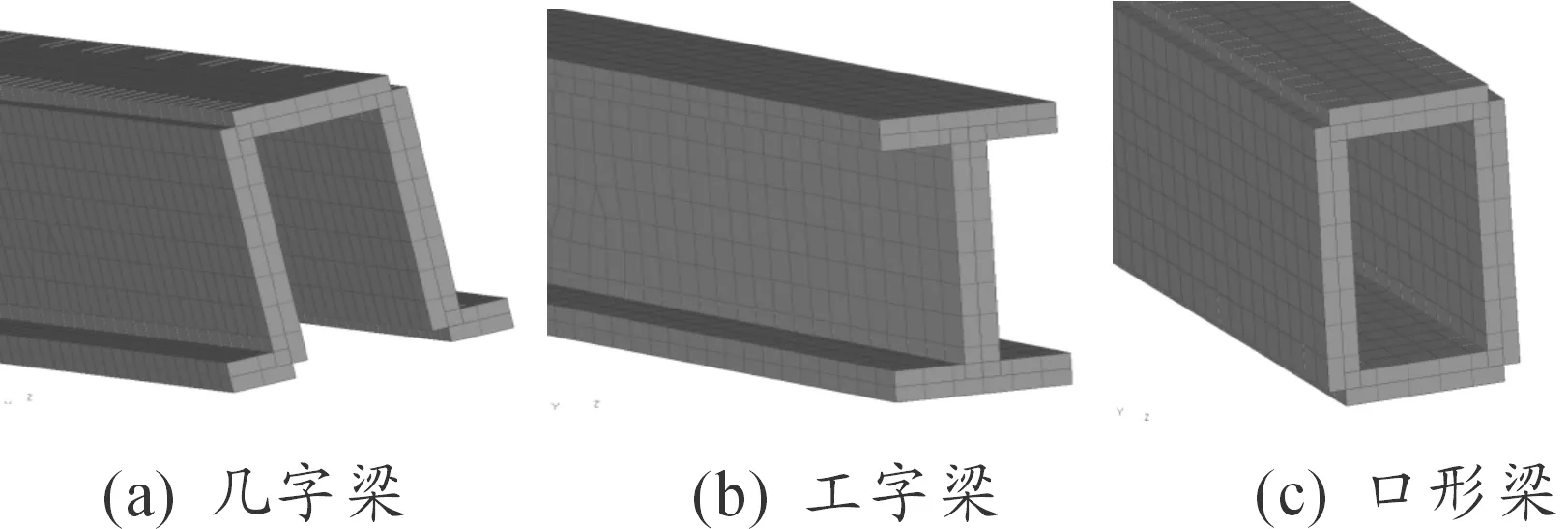
图7 梁结构模型截面示意图

2.2 三种梁结构防护性能对比

底甲板刚度是评价装甲车辆抗爆炸冲击能力的重要参考性能，而底甲板刚度可以通过底甲板的变形和应力大小来体现，底甲板的变形与应力愈小则底甲板刚度愈大，即车辆抗爆炸冲击能力愈强。

以同样的材料、高度、厚度及上表面宽度的三种梁在经过计算后的结果如表3所示，三种梁对应的底甲板应力云图如图8所示，三种梁对应的底甲板最大变形、内能和动能的曲线如图9、图10和图11所示。三种梁结构对应底甲板总体趋势基本一致，应力均主要集中在底甲板前半段，应力在底甲板前端约二分之一处两侧达到最大；车辆底部受到爆炸冲击后2.4 ms，底甲板内能到达峰值随后内能开始下降，最后趋于稳定；在车辆底部受到爆炸冲击后2 ms，底甲板动能到达峰值，随后逐渐衰减至0。从表中可以看到布置几字梁的底甲板方案的防护性能表现的更为优异一些，与工字梁的方案相比底甲板最大位移减少了3.70%，底甲板应力峰值减少了3.56%；与口形梁的方案相比底甲板最大位移减少了1.85%，底甲板应力峰值减少了1.73%；与原相比底甲板最大位移减少了32.08%，底甲板应力峰值减少了4.07%。

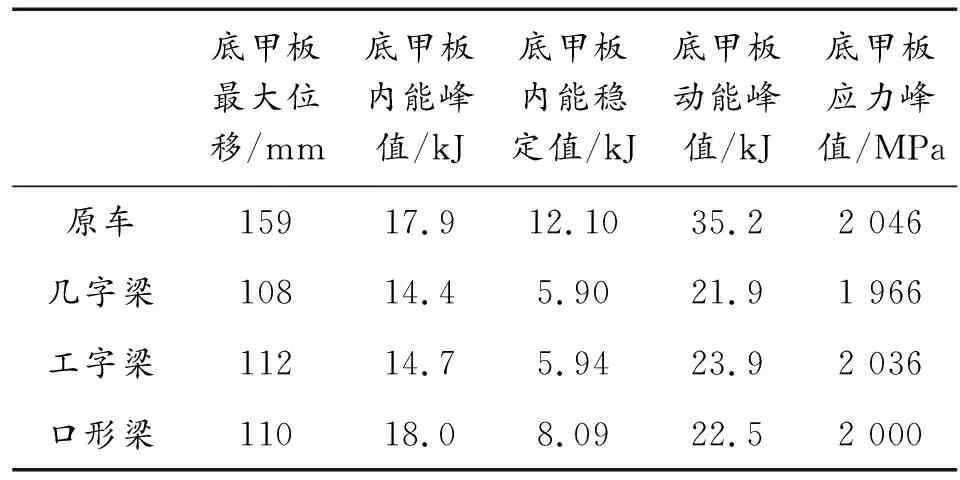
表3 三种梁防护性能

图8 各个梁结构对应底甲板合应力云图

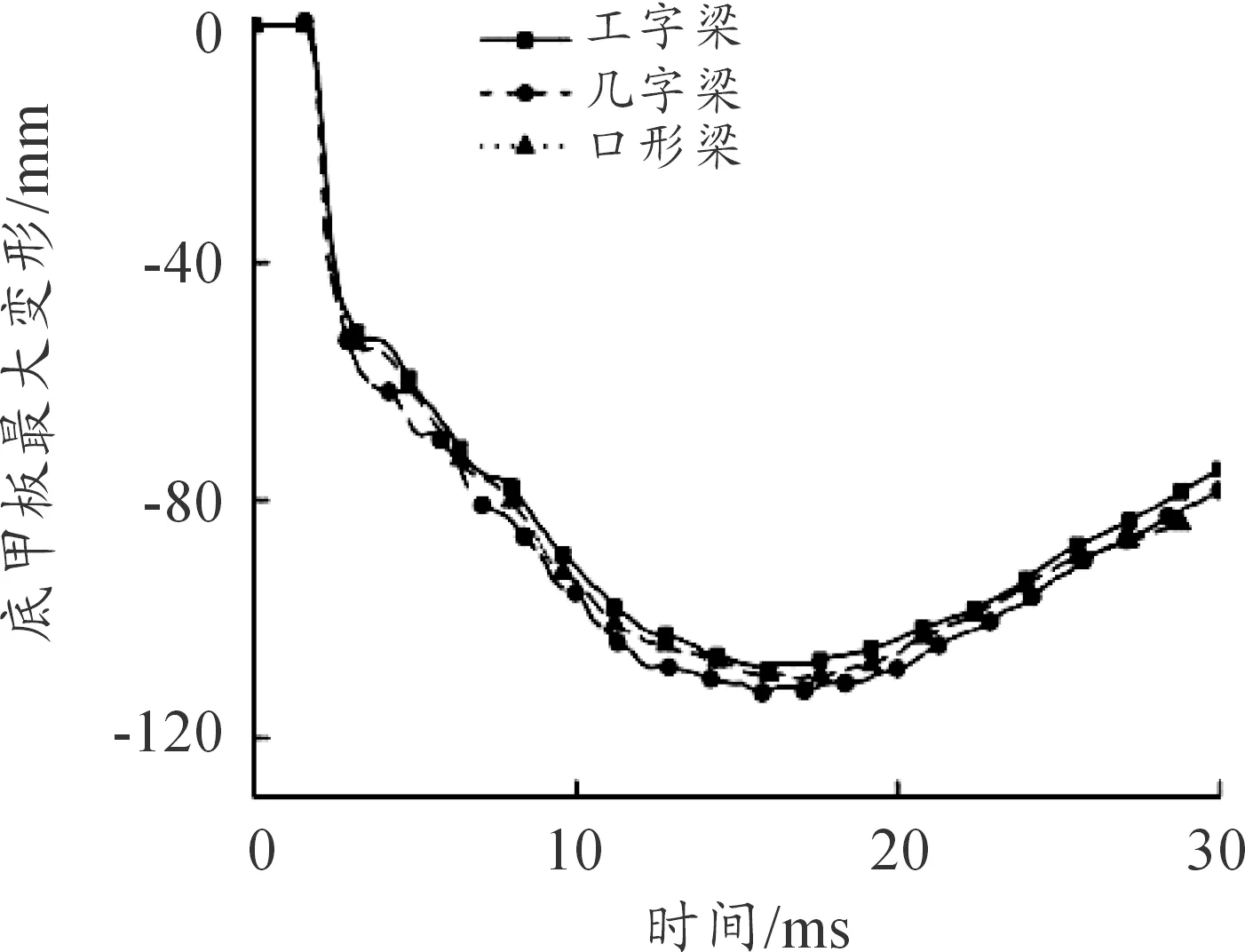
图9 底甲板位移曲线

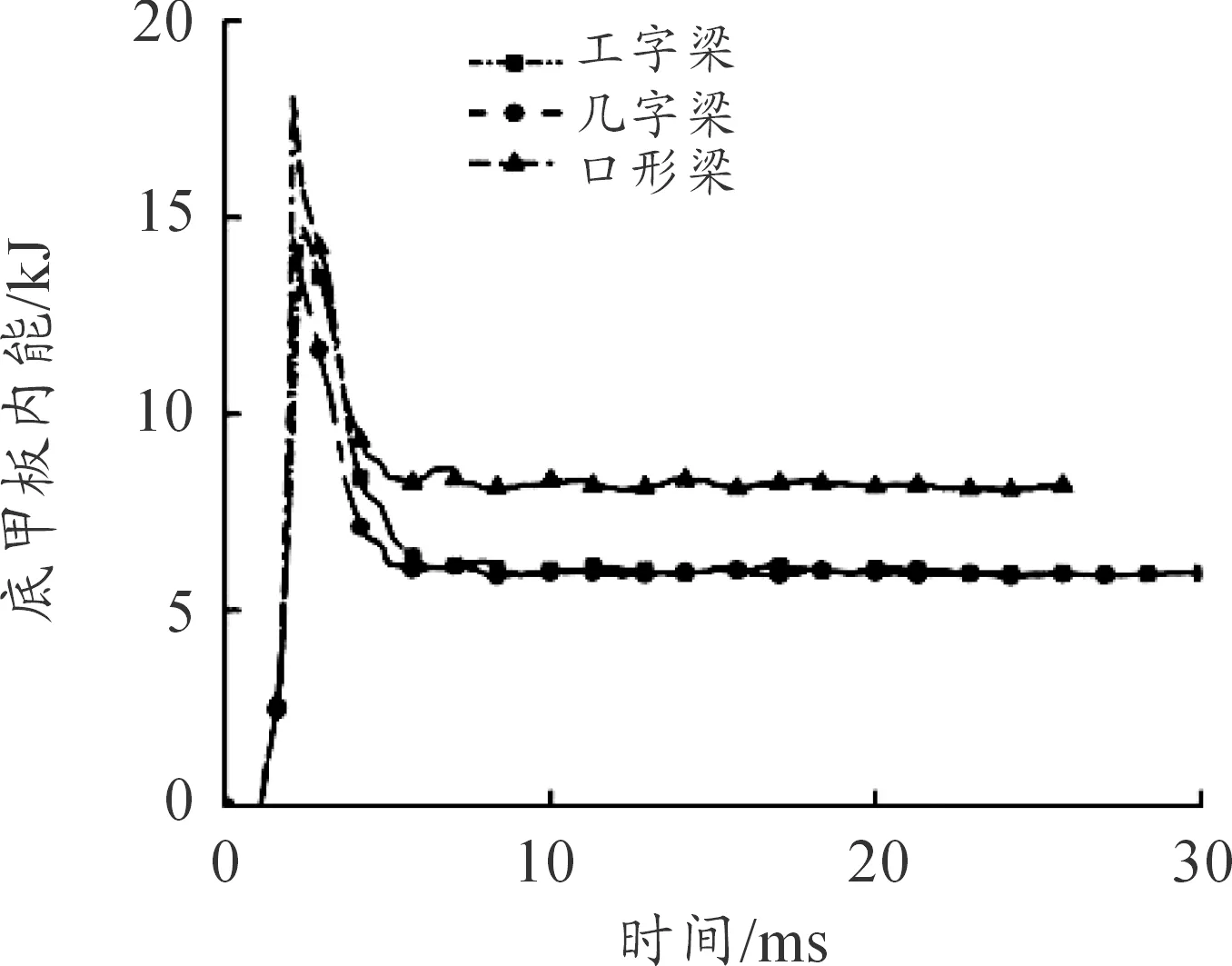
图10 底甲板内能曲线

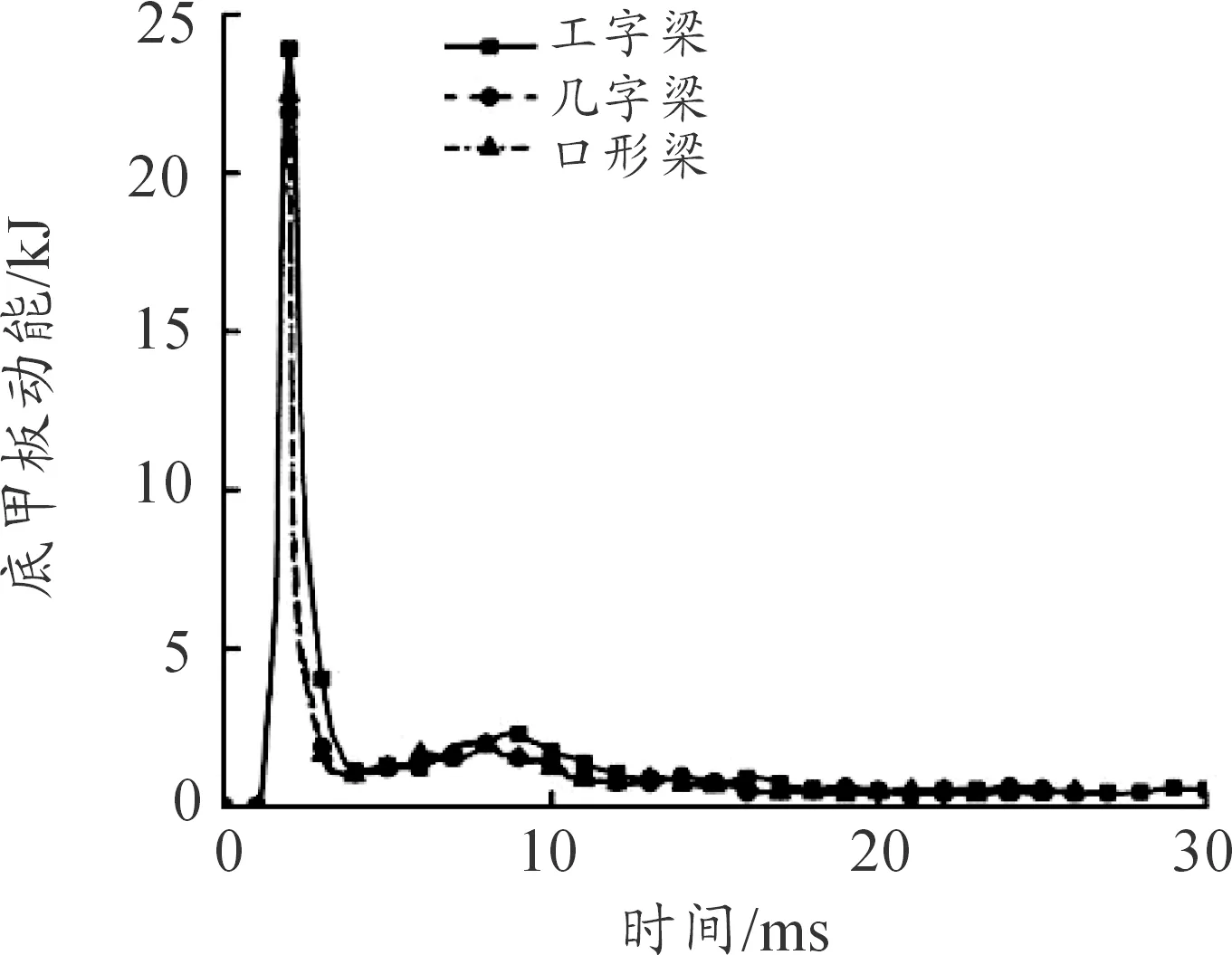
图11 底甲板动能曲线

3 梁结构优化设计

针对当前工程领域中复杂的优化问题，国内外将代理模型技术与多目标优化算法进行集成，开发出了一种高效的基于代理模型技术的多目标优化算法[12]，其优化设计流程框图如图12。

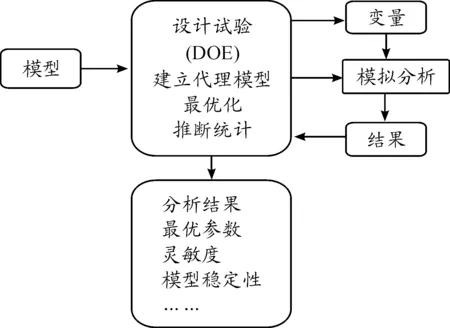
图12 优化设计流程框图

3.1 试验设计

基于拉丁超立方的方法进行试验设计，当响应面高度非线性时，采用该方法，默认运行次数是1.1×((N+1)×(N+2))/2，其中N是输入变量的数量。为了得到可重复的设计，必须维持随机变量的值。建立结构参数与目标函数的响应面模型。将梁的厚度T、杨氏模量E及屈服强度作为变量输入，3个变量的有关数值如表4所示，将底甲板的最大变形量D和应力S作为目标函数进行优化，对变量进行评估，得到11组采样点，针对11组采样点进行仿真分析，得到的数据如表5所示。

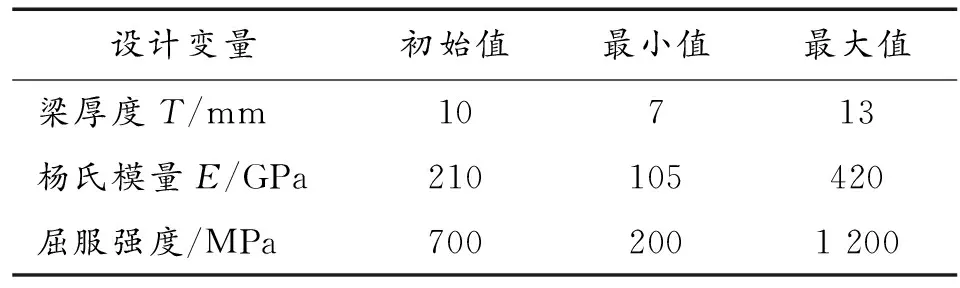
表4 初始设计变量值

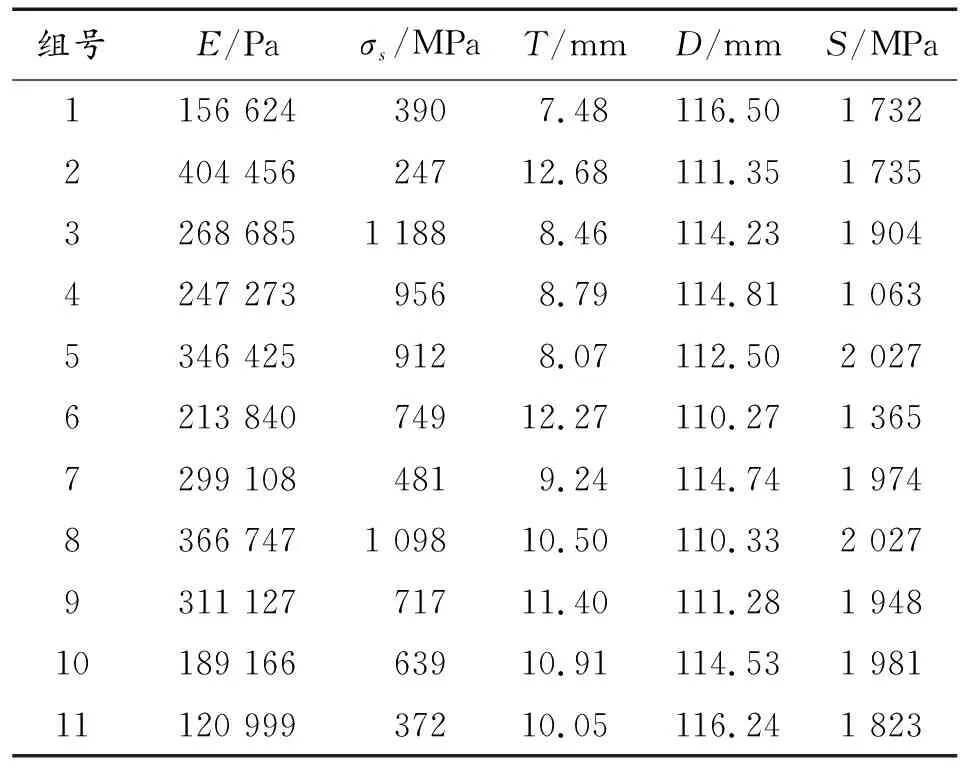
表5 DOE方案及对应数据

3.2 建立响应面模型及优化计算

基于Kriging最优内插法针对DOE建立响应面模型。Kriging是根据协方差函数对随机场进行空间建模和预测的回归算法。给定己知的样本点集X=[x1,x2, …,xn]T，样本点的响应值Y=[y1,y2, …,yn]T，其中xi(1≤i≤n)是m维向量，m为设计变量的个数，n为样本点个数。Kriging模型假设响应值与样本点之间的关系如下：

y(x)=f(x)+z(x)

(1)

其中f(x)是确定性部分，是对设计空间的全局近似，一般f(x)可以用一个常数用β表示。则式(1)可表示为：

y(x)=β+z(x)

(2)

z(x)为一随机函数，表示对全局近似的背离，它具有如下的统计特征：

E[z(x)]=0

(3)

Var[z(x)]=σ2

(4)

Cov[z(xi),z(xj)]=σ2Τ[R(xi,xj,θ)]

(5)

式(5)中T为相关函数矩阵，R(xi,xj,θ)为xi、xj之间的相关函数。

以底甲板最大变形量D和应力S为优化目标，同时对应力S进行上边界2 100 MPa和下边界1 000 MPa的约束，建立的3个变量与目标函数的响应面模型如图13所示。

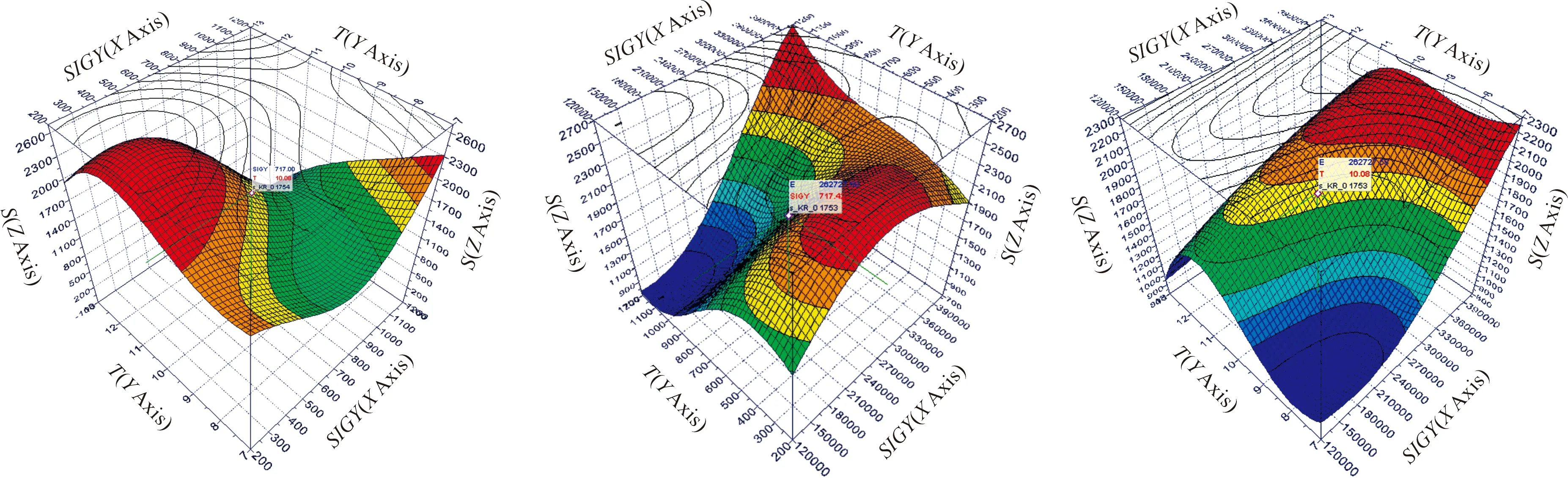
图13 响应面模型

图14显示表4所有采样点与代理模型拟合曲线的吻合程度，可以看到所有采样点都在拟合曲线上，因此代理模型稳定可靠。

基于多目标遗传算法(MOGA)对响应面模型进行求解，求解过程中，设置迭代次数为2 000次，遗传代数为50代，每代精英数量为样本空间的10%，变异率为0.1，最终得到帕累托解集1 913个，其拟合曲线如图15所示，结果如表6。

图14 响应面拟合曲线

图15 帕累托解集拟合曲线

表6 帕累托解集(部分)及变量参数

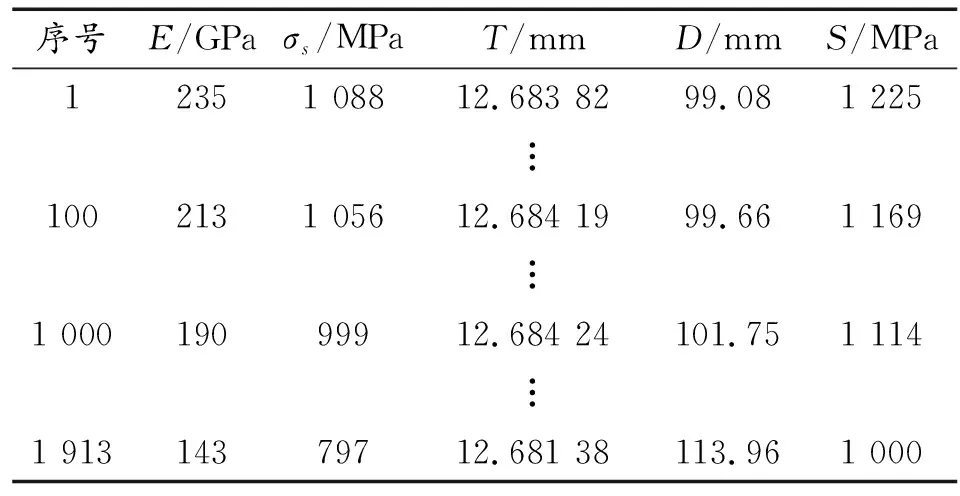
序号E/GPaσs/MPaT/mmD/mmS/MPa12351 08812.683 8299.081 225︙1002131 05612.684 1999.661 169︙1 00019099912.684 24101.751 114︙1 91314379712.681 38113.961 000

3.3 优化结果分析

因为优化的主要目标是底甲板的最大变形量，所以选择第一组解作为最优设计方案，与原始方案相比梁的杨氏模量增加25 GPa，屈服强度增加388 MPa，厚度增加2.68 mm，底甲板最大变形量减小了9 mm，最大应力减小了741 MPa。

由于该方案是由响应面模型预测所得，为了验证该结果是否可信，将对应数据代入有限元模型进行仿真，结果见表7，仿真值与优化结果的相对误差小于5%，证明所得到的最优解真实可靠。

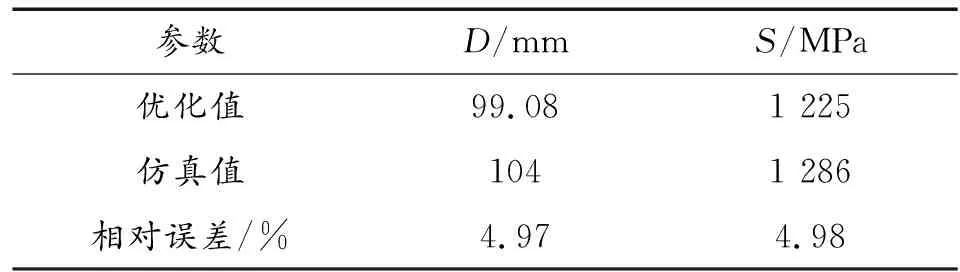
表7 优化值与仿真值

4 结论

1) 原车底部地板为对开的V形板，中部平板无加强梁结构，两侧斜板外侧梁结构较弱，导致车身底部结构刚度不足，防护能力不足。

2) 三种梁结构均能有效的提升车身底部结构刚度，明显减小底甲板的最大变形量，减小车内乘员损伤的可能性，但几字形截面梁对车辆底部结构抗爆炸能力最佳。

3) 利用多目标遗传算法(MOGA)对几字形截面梁优化设计，节省了计算资源，通过有限元模型检验，误差满足工程要求，使车辆底部结构抗爆炸能力再次提升。