多目标粒子群和人工蜂群混合优化的阈值图像分割算法*

赵 凤，孔令润，马改妮

(1.西安邮电大学通信与信息工程学院,陕西 西安 710121; 2.西安邮电大学电子信息现场勘验应用技术公安部重点实验室,陕西 西安 710121)

1 引言

随着目标识别、机器视觉的不断发展，图像分割技术越来越受到人们的重视。图像分割的目的是将一幅图像划分为多个感兴趣的区域，以便后续对这些区域进行进一步处理。目前常用的分割方法主要包括基于阈值的分割方法[1]、基于区域的分割方法[2]和基于聚类的分割方法[3]等。在诸多的图像分割方法中，基于阈值的图像分割方法因其性能稳定、算法简单等特点，一直是图像分割领域中的热门研究方向。其中，最大类间方差法(Otsu)[4]、最大熵法(Kapur)[5]由于其原理简单，易于实现，因此是最常见的2种阈值分割算法。但是，上述算法对于双峰不明显的复杂图像分割效果不佳；而且在进行多阈值图像分割时，由于计算量过大，效率太低，往往也不能得到理想的分割结果。

为了解决上述问题，有学者将粒子群优化PSO(Particle Swarm Optimization)算法[6]和人工蜂群ABC(Artificial Bee Colony)算法[7]等生物启发式算法应用到阈值图像分割[8 - 11]中。文献[8]针对二维Otsu算法计算量过大的缺点，采用PSO算法寻找最优的二维阈值向量，实验结果表明，该算法在取得较为理想分割结果的同时，大大减少了计算量。文献[9]提出了一种基于ABC优化的阈值图像分割算法，将最大熵函数作为需要优化的目标函数，可以得到良好的分割结果。需要指出的是，PSO算法和ABC算法在优化的后期阶段都存在一些问题[12,13]，PSO算法易陷入局部最优，而ABC算法的全局搜索能力虽然强，但局部搜索能力较弱，不能达到一个很好的平衡。因此，有学者结合ABC算法与PSO算法的优点，提出了ABC算法和PSO算法相结合的混合优化算法[14,15]。文献[15]在PSO算法中引入人工蜂群搜索算子，利用人工蜂群算子具有较强的全局探索能力的特点，对粒子的历史最优位置进行搜索，从而避免陷入局部最优。

然而，上述方法都只是单个阈值准则下的优化问题，无法满足用户多方面的需求，因此多个阈值准则下的图像分割问题越来越值得研究。近年来，多目标优化算法被用到阈值图像分割[16 - 18]中，与其他单目标的阈值分割算法相比，多目标优化算法在多个阈值准则之间协调权衡，尽量使得各个阈值准则都达到最优。在文献[17]中，Nakib等人提出了利用第2代非支配排序遗传算法NSGA-Ⅱ(Non-dominated Sorting Genetic Algorithms-Ⅱ)[18]同时优化改进的类间方差、香农熵和2-D熵函数这3个目标函数。

本文针对多阈值分割问题，利用PSO算法开采能力强而ABC算法注重探索能力的特性，提出了基于多目标粒子群和人工蜂群混合优化MPS-ABC(Multi-objective Particle Swarm and Artificial Bee Colony hybrid optimization)的阈值图像分割算法。该算法采用改进的最大类间方差准则和最大熵准则作为多目标进化的2个适应度函数，提出了一种粒子群和蜂群的混合进化策略，并对ABC算法的搜索策略进行了改进，在进化过程中每隔1代进行1次信息的交互，避免由于错误的信息判断而陷入局部最优的问题，从而能够更加有效地逼近最优阈值。本文将最大类间方差法[4]、最大熵法[5]、基于最大熵的人工蜂群阈值MEABCT(the Maximum Entropy based Artificial Bee Colony Thresholding)图像分割算法[9]、基于Otsu标准的多级阈值粒子群优化算法[19]PSO-Otsu(Particle Swarm Optimization algorithm for multilevel thresholding by the criteria of Otsu)、多目标人工蜂群优化MOABC(Multi-objective Optimization method based on the Artificial Bee Colony)算法[20]和基于多目标粒子群优化MOPSO(Multi-Objective Particle Swarm Optimization)的阈值图像分割算法[21]作为对比算法。实验结果表明，本文算法对于目标和背景复杂的多阈值图像的分割，不但缩短了计算时间，而且还能取得较为理想的分割结果。

2 粒子群优化算法和蜂群算法的基础理论

2.1 粒子群优化算法

PSO算法[6]是模拟鸟群觅食行为的一种优化算法。PSO算法首先在搜索空间内生成1组均匀分布的粒子xi=(xi,1,xi,2,…,xi,D),i= 1,2,…,N，N表示种群规模，D表示粒子的维度。每1个粒子会有1个速度来决定飞行的距离和方向，速度的更新是由当前粒子经历过的最好位置以及所有粒子在每次迭代中得到的最好位置决定的。粒子的速度更新如式(1)所示：

(1)

对于每1个粒子xi，更新方式如式(2)所示：

xi,j(t+1)=xi,j(t)+vi,j(t)

(2)

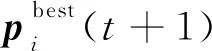
(3)

其中，f是目标函数。

全局最优解gbest由式(4)计算得出：

(4)

2.2 人工蜂群算法

在ABC算法[7]中，蜂群由雇佣蜂、跟随蜂和侦察蜂3个部分组成，整个蜂群的目标是寻找花蜜量最大的蜜源，即优化问题中的最优解。雇佣蜂的数量和跟随蜂的数量是相等的。雇佣蜂的作用是搜索花蜜源并把蜜源信息传递给跟随蜂；跟随蜂根据蜜源的丰富程度采用轮盘赌的方式选择蜜源进行跟随，并在蜜源周围进行搜索；如果蜜源经过多次更新没有改进，则放弃该蜜源，雇佣蜂变为侦查蜂随机搜索新蜜源。在ABC算法中，每个蜜源代表优化问题的1个可能解，蜜源的花蜜量(解的优劣)是通过适应度值来评定的。雇佣蜂的数量等于蜜源的数量。

假设问题的解空间是D维的，则第i个蜜源的位置可以表示为1个D维的向量xi=(xi,1,xi,2,…,xi,D),i= 1,2,…,N，N代表蜜源的数量。ABC算法各个阶段的细节如下所示：

在种群的初始化阶段，根据式(5)来随机产生蜜源的位置:

(5)

在雇佣蜂阶段，雇佣蜂会在蜜源周围进行搜索，并按照式(6)产生新的个体x′i，每1个蜜源对应1个变量trial来记录该蜜源连续未被改善的次数，若某一蜜源的trial值超过限定的循环次数l，则对应雇佣蜂转化为侦察蜂随机搜索新蜜源。

x′i,j=xi,j+rand()·(xi,j-xk,j)

(6)

其中，j是{1,2,…,D}中随机选择的整数，代表雇佣蜂随机地选择可行解的一维进行更新搜索；xk,j表示在蜜源中随机地选择1个不同于xi,j的蜜源。

在跟随蜂阶段，跟随蜂会评估雇佣蜂带回的花蜜量的信息，并采用轮盘赌的方法选择雇佣蜂进行跟随。跟随蜂选择雇佣蜂的概率计算如式(7)所示:

(7)

其中，fit(xi)代表第i个蜜源的花蜜量。

在侦查蜂阶段，如前文所述，若1个蜜源经过l次循环之后不能被改进，则该蜜源被放弃，同时，该蜜源处的雇佣蜂成为侦察蜂，侦查蜂会根据式(5)产生1个新的蜜源。

通过分析以上2种算法可以得出：PSO算法更侧重于开采能力，局部搜索能力更强，但是容易陷入局部最优；而ABC算法则更加注重探索能力，全局搜索能力相对更强。因此，本文结合PSO算法和ABC算法各自的优点，提出了一种基于粒子群和蜂群的混合优化算法MPS-ABC,并将其用到图像分割中，以达到更好的分割效果。

3 基于多目标粒子群和人工蜂群混合优化的阈值图像分割算法

3.1 种群初始化及编码

本文所提出的MPS-ABC算法是对图像的阈值进行编码，编码方式采用实数制编码，编码范围是[Imin,Imax]，其中Imax和Imin分别表示图像像素的最大值和最小值。本文算法使用式(5)来生成初始种群，并将生成的种群随机等分为种群Q1和种群Q2，使其分别作为PSO算法和ABC算法的初始种群。

3.2 适应度函数的构造

适应度函数主要用于评价种群中个体的优劣性。本文将改进的类间方差函数和最大熵函数作为待优化的适应度函数。设1幅图像总的像素数目为C，其灰度级为[0,255]，Ci表示像素值为i的像素个数，则像素值i出现的概率pi由式(8)计算得出：

(8)

设图像的阈值为t1,t2,…,tn，改进的最大类间函数定义如下：

(9)

其中，

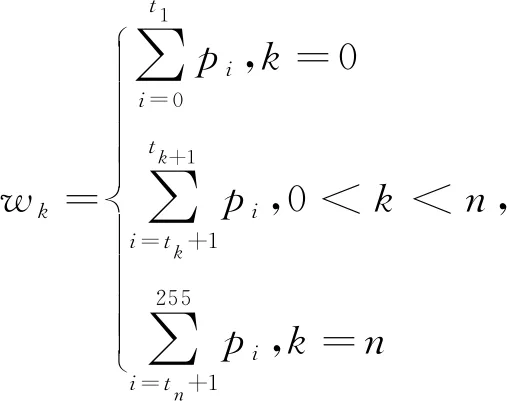
最大熵函数的定义如下：

H(t1,t2,…,tn)=H0+…+Hk+…+Hn

(10)

其中,H0,…,Hk,…,Hn分别计算如下：

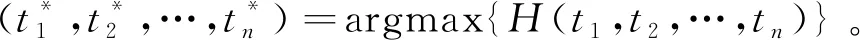
3.3 粒子群和蜂群的混合优化策略

在3.1节得到2组初始种群，Q1按照PSO算法进行寻优，个体的更新采用式(2)进行；Q2按照ABC算法进行寻优，为了保证算法的探索能力，同时提高开采能力，在ABC算法中的雇佣蜂阶段提出了新的搜索方程[22]：

(M(x)-xk)+A(i)·(xi-xk)

(11)

A(i)=(1+trial(i))-0.2+0.1·rand()

(12)

其中，trial(i)代表第i个个体连续未更新的次数。

由于新的搜索方程(11)中引入了最优解，因此在提高开采能力的同时也保证了算法的探索能力，能够让该算法在全局搜索与局部搜索之间达到更好的平衡。与此同时，算法在混合优化的过程中，每隔1次迭代会利用1种信息交流机制进行信息的交互，避免错误的信息判断而陷入局部最优解。种群之间的信息交流机制如下所示：

(1)在蜂群的进化过程中，将粒子群更新后的解作为蜂群的初始种群，并在雇佣蜂阶段比较式(11)产生的解yi、原解xi和粒子群中的全局最优解gbest的适应度值，保留最优个体。经过l次循环之后，若还未找到更优解，则放弃原来的解，并按照式(5)产生1个新解。

3.4 最优解的选择

本文采用多目标方法进行优化，每次迭代产生的解都会根据拥挤距离进行非支配排序，并保留非支配解，因此经过上述步骤会获得一组非支配解集。但是，在实际应用中，我们往往只需要1个最优解。本文通过计算每个非支配解的类间差异和类内差异的加权比值F[23]来选取种群的最优解,并对其中的类内差异进行扩展，选取使得F取最大值的个体作为种群最优解。加权比值F的定义如下所示：

(13)

(14)

其中，xij表示第j类中的第i个像素的灰度值。

Figure 1 Segmentation results on #3096图1 #3096分割结果

Figure 2 Segmentation results on #24063图2 #24063分割结果

3.5 混合优化算法的流程

混合优化算法的流程如下所示：

步骤1设置种群的规模N，最大迭代次数Tmax，局部循环次数l，学习因子c1和c2，惯性权重w。

步骤2由式(5)进行种群初始化，并将种群随机等分为2个种群Q1和Q2。

步骤3设置初始的迭代步数iter=0。

步骤4种群Q1按照式(11)产生新解，种群Q2按照式(2)产生新解，分别计算新产生解的适应度值。对所有解进行评估，保留非支配解，实现对非支配解集的更新。

步骤52个种群每隔1代进行1次信息的交互。

步骤6更新迭代步数iter=iter+1，当算法迭代达到Tmax次时终止，输出找到的解集，否则转至步骤4。

步骤7从得到的1组非支配解集中，根据加权比值F选择最终解。

4 实验结果与分析

为了验证本文算法的性能，采用Otsu算法、Kapur算法、MEABCT算法、PSO-Otsu算法、MOABC算法和MOPSO算法作为比较算法。实验分为2个部分：第1部分采用多幅Berkeley图像进行验证，第2部分用核磁共振(MR)图像进行分割实验。本文所提出的MPS-ABC算法和6种对比算法的参数设置如下：本文算法以及其他6种对比算法的种群规模均设置为30，最大迭代次数为100；MEABCT算法和MOABC算法的局部循环次数设置为100，PSO-Otsu算法中的c1和c2都取1.8，w0取3，ri(t) 是0～1的随机数；MOPSO算法和本文算法的学习因子c1=1，c2=2，惯性权重w=0.5。

Figure 3 Segmentation results on #241004图3 #241004分割结果

Figure 4 Segmentation results on #55067图4 #55067分割结果

4.1 Berkeley图像对比实验

本节采用多幅Berkeley图像来验证算法的分割性能。在Berkeley图库中选择图像#3096、#24063、#241004、#55067作为实验对比图。分割结果如图1～图4所示，其中a～i分别展示的是原图像、标准分割图、Kapur算法、Otsu算法、MEABCT算法、PSO-Otsu算法、MOABC算法、MOPSO算法和MPS-ABC算法的分割结果。此外，本文采用图像分割准确率来客观评价算法的分割结果，相应的结果如表1所示。表2给出的是本文算法和对比算法在6幅Berkeley图像上得到的最优分割阈值。

由图1～图4可以明显看出，本文算法相对于其他6种对比算法能够取得更好的分割结果。对于图像#3096，可以看出Kapur算法、Otsu算法、MEABCT算法和PSO-Otsu算法都在图像的左下角存在明显的错分，本文算法相比于这4种算法在视觉效果方面明显取得了更好的分割效果。在图2中，Kapur算法、Otsu算法、MEABCT算法、PSO-Otsu算法和MOABC算法对于右上角的天空以及门前的栅栏都存在错分；而MOPSO算法虽然能分清门前的栅栏，但对于右上角的天空那一部分处理不佳；而本文算法借鉴了ABC算法的进化策略，并且对ABC算法的进化策略进行了改进，所以相对于MOPSO算法来说更容易跳出局部最优以找到最优阈值，因此对门前的栅栏和右上角的天空都取得了良好的分割效果。

Table 1 Segmentation accuracy values of all algorithms on Berkeley images表1 所有算法在Berkeley图像上的分割准确率

Table 2 The best thresholds of all algorithms on Berkeley images表2 所有算法在Berkeley图像上的最优分割阈值

根据表1的准确率对比也可以明显看出，本文所提出的MPS-ABC算法相较于其他6种对比算法，在大多数图像上都取得了较高的分割准确率。例如，对于图像#135069，本文算法的分割准确率可以达到0.991 6，而Otsu算法和MEABCT算法的分割准确率分别为0.554 1和0.605 5；对比多类分割图像#55067的分割准确率结果，本文算法的分割准确率为0.921 0，相对于Kapur算法在准确率方面提高了0.118 4，比PSO-Otsu算法高出0.230 6。

通过比较本文算法与其余6种对比算法在准确率以及视觉效果上的差异可知，本文算法的寻优能力更强，能够更加有效地逼近最优阈值。

为了验证本文算法的有效性，图5给出了Kapur算法、Otsu算法、MEABCT算法、PSO-Otsu算法、MOABC算法、MOPSO算法和MPS-ABC算法在多幅Berkeley图像下的平均PR曲线对比图。通过图5可以看出，本文算法性能优于其他6种对比算法。

Figure 5 PR curves comparison of each algorithm图5 各个算法的PR曲线对比

与已有的Otsu算法与Kapur算法相比，本文算法在多阈值情况下不但分割效果有所提升，运行时间也大大降低。图6给出了本文算法与Otsu算法、Kapur算法、MOPSO算法以及MOABC算法在5幅阈值图像#55067下的运行时间对比。可以看出，本文算法相较于Otsu算法和Kapur算法不但分割效果更好，而且运行时间大大降低。而相较于MOPSO算法和MOABC算法，本文算法在运行时间基本相同的情况下，分割效果更好。

Figure 6 Run time comparison of each algorithm图6 各算法的运行时间对比

4.2 MR图像对比实验

为了进一步验证本文算法的性能，本节选择来自互联网脑分割库IBSR(The Internet Brain Segmentation Repository)的MR图像进行分割实验，并用图像分割准确率作为评价标准。如图7～图9所示为本文算法与其他6种对比算法在3幅MR图像上的分割结果；对比算法和本文MPS-ABC算法的准确率如表3所示。

Figure 7 Segmentation results on the slice 12 of image 12-3图7 图像12-3切片号为12的分割结果图

Figure 8 Segmentation results on the slice 50 of image 2-4图8 图像2-4切片号为50的分割结果图

Figure 9 Segmentation results on the slice 45 of image 100-23图9 图像100-23切片号为45的分割结果图

从视觉效果看，本文算法能够取得较为理想的分割结果。由图7～图9中可以看出，本文算法相较于Kapur算法、PSO-Otsu算法、MOABC算法、MOPSO算法能够有效地分清灰质和白质，在视觉效果上有了明显的提升；而Otsu算法和MEABCT算法虽然能大致分清灰质和白质，但本文算法在一些细节处理方面的性能更优。

分析表3中的分割准确率可以看出，本文算法相对于其他对比算法能够取得更好的分割结果。对于图像2-4，切片号为7时，本文提出的MPS-ABC算法的准确率为0.973 3，而Kapur算法、PSO-Otsu算法和MOPSO算法的准确率分别为0.938 6,0.925 1和0.944 4；对于图像110-3，切片号为37时，本文算法的准确率为0.935 6，相对于Kapur算法提升了0.053 7，相较于MEABCT算法准确率提高了0.053 5，比MOPSO算法的准确率高出0.064 7。

综合各算法在图像分割准确率和视觉效果上的表现可知，本文所提出的MPS-ABC算法的性能更好，能够得到更优的分割结果。

5 结束语

将粒子群和蜂群的混合优化策略引入到阈值图像分割算法中，使算法在全局和局部搜索能力之间建立一个良好的平衡。同时将多目标优化引入到阈值图像分割中，采用改进的最大类间方差和最大熵2个准则作为该算法的目标函数；在ABC算法的进化过程中对搜索方程进行了改进，增强了算法的寻优能力，避免种群陷入局部最优，使得算法能更加有效地逼近最优阈值，获得更加好的图像分割效果。

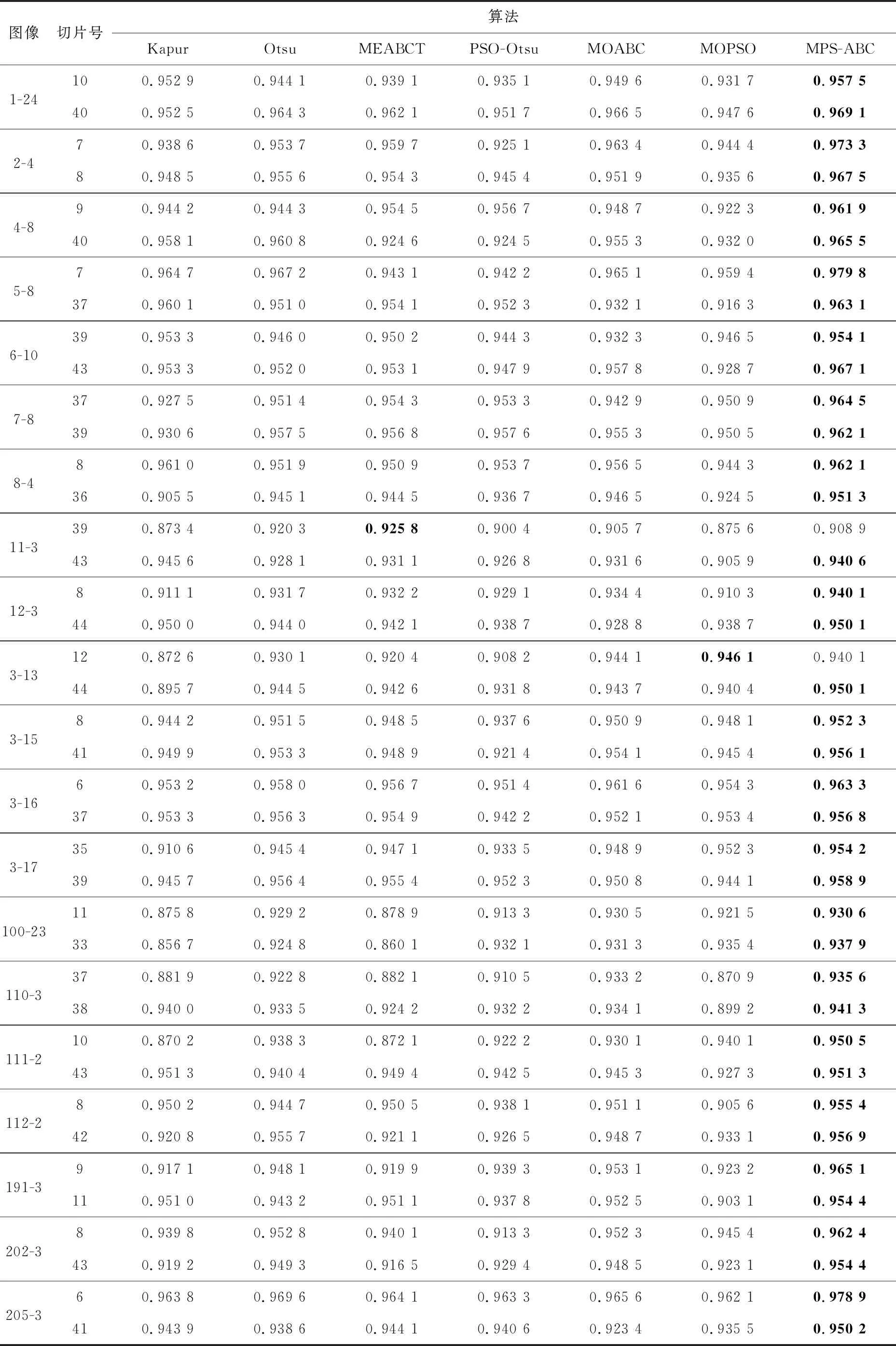
Table 3 Segmentation accuracy values of all algorithms on MR images 表3 所有算法在MR图像上的分割准确率

本文算法的阈值数目是提前设定好的，因此如何自适应地确定图像阈值数目是我们下一步的研究方向。此外，阈值图像分割对噪声比较敏感，因此如何利用图像的空间信息，使得被噪声污染的图像能够取得良好的分割结果将是一个非常有意义的研究方向。