制冷压缩机电机转子不平衡电磁力计算与改善

张 申，王孚懋，张玉环，张 娜，徐基超

（1.山东科技大学，山东青岛 266000；2.瑞智（青岛）精密股份有限公司，山东青岛 266000）

0 引言

电机转子偏心是制冷压缩机常见的故障之一，主要分为静偏心、动偏心以及混合偏心。静态偏心一般是由制造安装误差、定子铁芯椭圆以及转子临界速度引起振动等原因造成；动态偏心一般由转轴弯曲、轴承磨损、严重的静态偏心等因素造成的；混合偏心，则兼有上述两种偏心的特点。对于旋转式压缩机，其电机转子采用悬臂梁安装方式，难以保证定子与转子的中心轴线重合，易造成电机转子静偏心。针对转子偏心，众多学者进行了大量的研究。文献［1］应用麦克斯韦应力张量法计算了转子不平衡磁拉力，将解析结果与有限元计算进行对比，得到静态偏心和动态偏心不平衡磁拉力均随着偏心距的增加而增大。文献［2］运用麦克斯韦张量法计算了永磁及铁磁材料电磁力，大型感应电动机发生短路故障时，径向与切向转子电磁力波幅值分别达到了正常状态下的2.4 倍和2.7 倍。文献［3］采用三维有限元法计算了汽轮发电机端部电磁场分布，得到了端部电磁力的精确分布，与试验分析结果是吻合的。文献［4］计算了大型感应电动机单相短路故障时的动态电磁力以及某笼型感应电动机径向电磁力。文献［5］计算了转子静态与动态偏心时，电磁转矩的变化量及定子侧受到的径、切向电磁力，得到了转子偏心引起电机内电磁场不对称分布，且气隙磁密度随偏心距离增加而增大。在研究电机故障方面，文献［6］结合模糊算法对螺杆式空气压缩机进行了故障分析与诊断。文献［7-10］利用粗糙集理论和小波能量谱理论相结合的方法，对活塞式压缩机进行故障诊断研究，提高了活塞压缩机故障诊断的有效性和准确性。

以制冷压缩机配套的S55202N-U1FN 单相异步电机为样机，采用麦克斯韦张量法，将交流电磁铁理论应用于电机转子径向不平衡磁拉力的计算，利用Ansoft Maxwell 软件计算电机转子在不同偏心程度时产生的径向电磁力，并将计算结果导入Ansys workbench 中，求得转子在受到最大磁拉力时产生的形变量，并在原有工艺改造项目中进行了验证方案的有效性。

1 不平衡磁拉力计算

求电磁力方法有麦克斯韦张量法和交流电磁铁理论［11］。

应用麦克斯韦张量法，某点或某线上的切向力和径向力的计算式分别是：

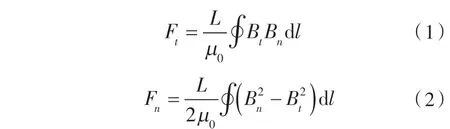
式中 Ft，Fn——径向与切向电磁力，N；

Bt，Bn——径向与切向磁通密度；

L ——导线长，m；

μ0——真空磁导率，取 μ0=4π×10-7N·A-2。

电磁铁分为直流与交流两类，直流电磁铁的吸附力为恒定值。交流电磁铁的吸附力是大小变化的。根据交流电磁铁理论，气隙中电磁铁对衔铁的吸附力计算式为：

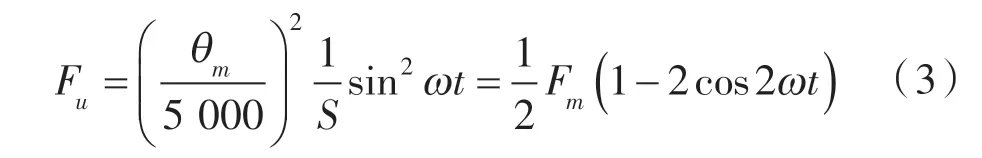
式中 θm——磁通量的幅值，M；

S ——气隙界面面积，cm2；

ω ——频率，rad/s；

Fm——幅值，N。

由式（3）可知，交流电磁铁吸附力平均值 Fm/2，幅值为Fm，最小值为0，频率为电频率的 2 倍。

以电机主、副绕组中心线划分电机，可以得到4 个气隙，分别求这个4 个气隙中电磁力，其合力就是转子受到的径向力，其中F 表示在发生转子偏心时产生的不平衡磁拉力；θ表示F 与主线圈中心线的的夹角；Δ 表示转子偏心的距离。转子不平衡径向力如图1 所示。

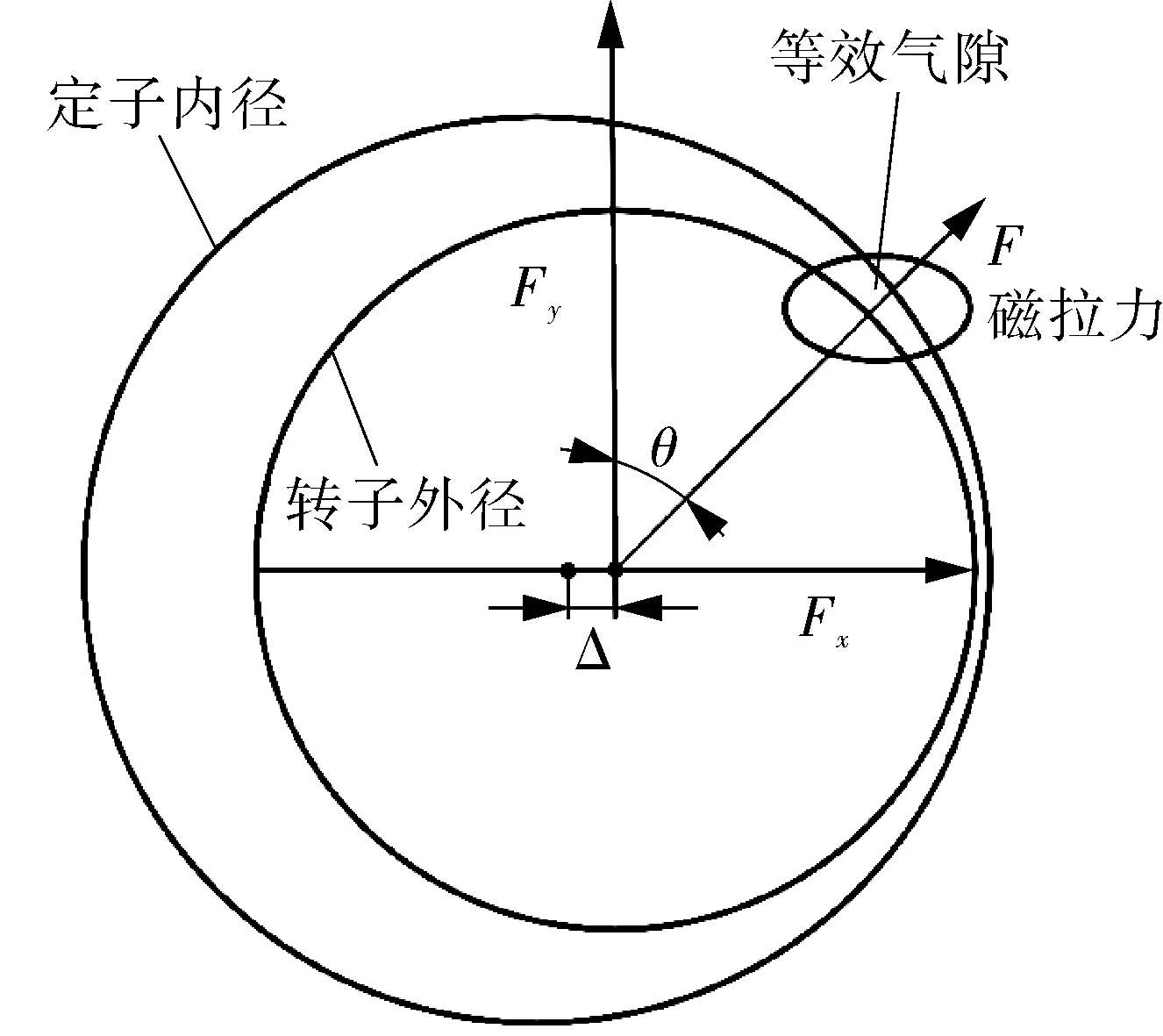
图1 转子不平衡径向力示意

不平衡磁拉力按下式计算［8］：

式中 δ0——电机设计气隙，mm；

θ ——等效磁拉力夹角度数，°。

由式（4）可知，确定不平衡磁拉力时，需要计算转子径向力角度θ。首先求齿磁导，可得总的磁通量θm（匝数×总磁导）见表1。

表1 机槽匝数与齿磁导

根据各齿的磁导大小来分配磁通量。求出每个定子齿的磁通量、X 方向总分量和Y 方向总分量，求得 θ 角度见表2。

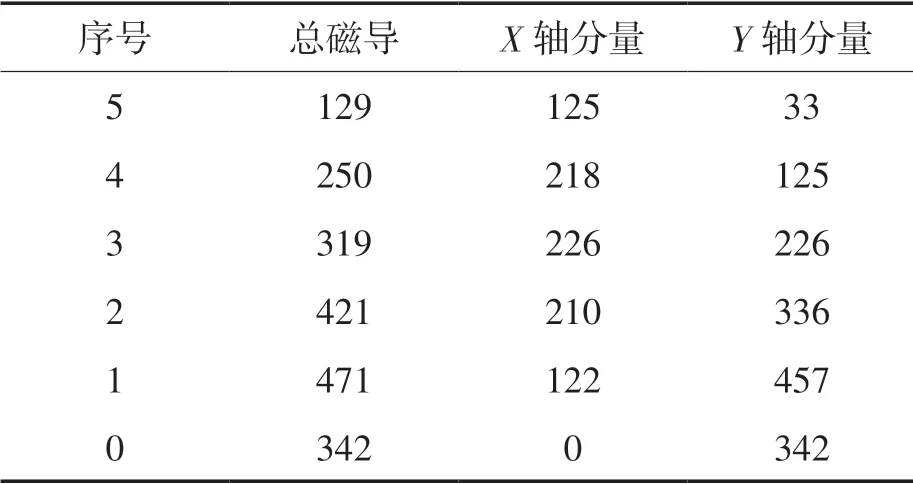
表2 总磁导与X 轴Y 轴分量 H

由表2 可知在X 轴的总磁导为901，在Y 轴上的总磁导为1 519，所以可以求出径向力电磁力与Fy轴之间的夹角 θ 的大小为59.325°。

气隙面积计算：

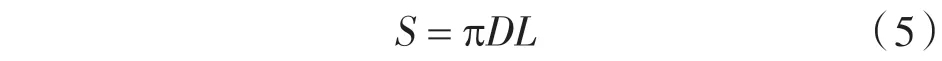
式中 D —— 磁密度积分路径所对应直径，D= 6.4 cm；

L ——电机轴向长度，L=17.42 cm。

将求出的 θ 角度与气隙面积代入式（4），可求任意偏心距离的不平衡磁拉力。将求得的转子径向力角度 θ ，气隙积S，代入到式（4）中，例如当转子偏心距Δ 为0.05 mm 时，其转子在单位面积上所受径向不平衡磁力为117.8sin2ωt N。

2 径向不平衡磁场力有限元分析

采用Ansoft maxwell 软件可以对电机或电磁铁进行电磁场、电磁力的仿真计算。在Ansoft maxwell 中有二维、三维以及RMxprt 3 种电机分析模块。

软件自动生成电机二维模型如图2 所示。

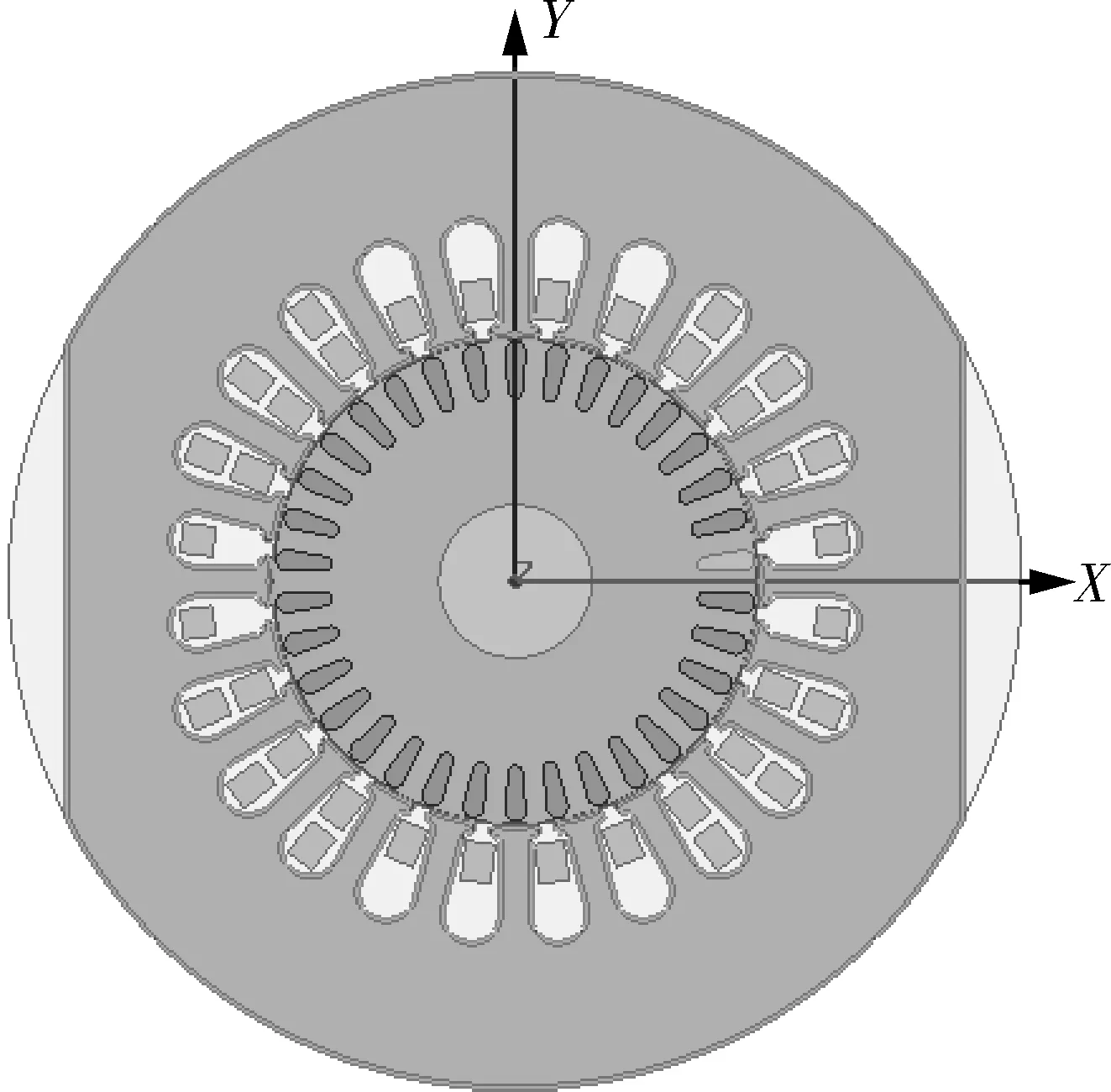
图2 电机模型

本文使用RMxprt 模块进行电机的建模分析，该模块基于等效电路和磁路的计算方法，而且该模块基本囊括了工业生产所需要的各种电机。选择单项异步电机，添加RMxprt 材料库，选择硅钢片材料属性，设置定子与转子参数，其中主要参数为定子铁芯外径为139.14 mm，内径为67.32 mm，轴向长度为107 mm，槽型代号为2，槽数24。设置转子参数，外径66.294 mm，内径21.02 mm，轴向长度107 mm，槽型代号为2，槽数34。

转子不同情况下受到的径向不平衡磁拉力见表3。

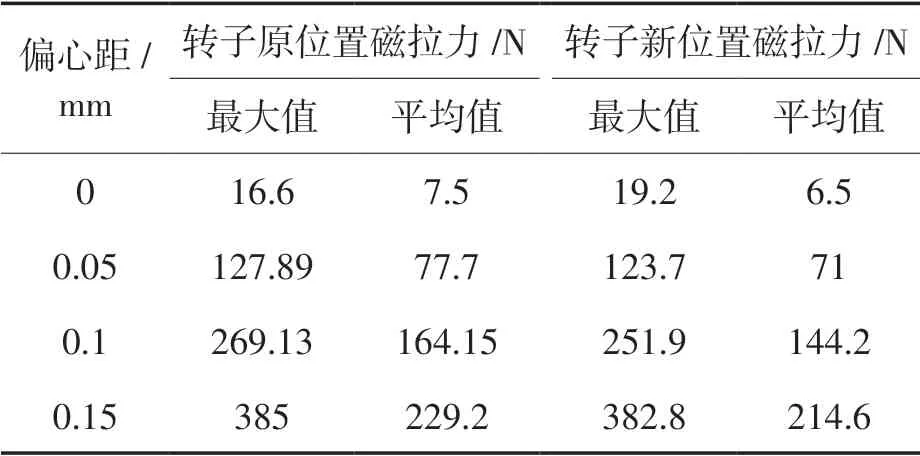
表3 不平衡磁拉力

当转子由于位置与偏心程度不同时，受到的最大径向力与理论计算值进行对比如图3 所示。由图3 可以看出理论计算公式得到的结果与实际计算得到的结果接近，并且改善后的转子受到的径向磁拉力有所减小。

图3 转子所受径向磁拉力比较

3 转子-泵浦系统强度分析

在做启动测试时，如果转子发生偏心，会导致转子受到径向不平衡电磁力产生弯曲变形，使电机定转子发生摩擦碰撞，损坏电机。建立转子-泵浦系统模型如图4 所示，转子通过过盈配合与偏心转子组合在一起。

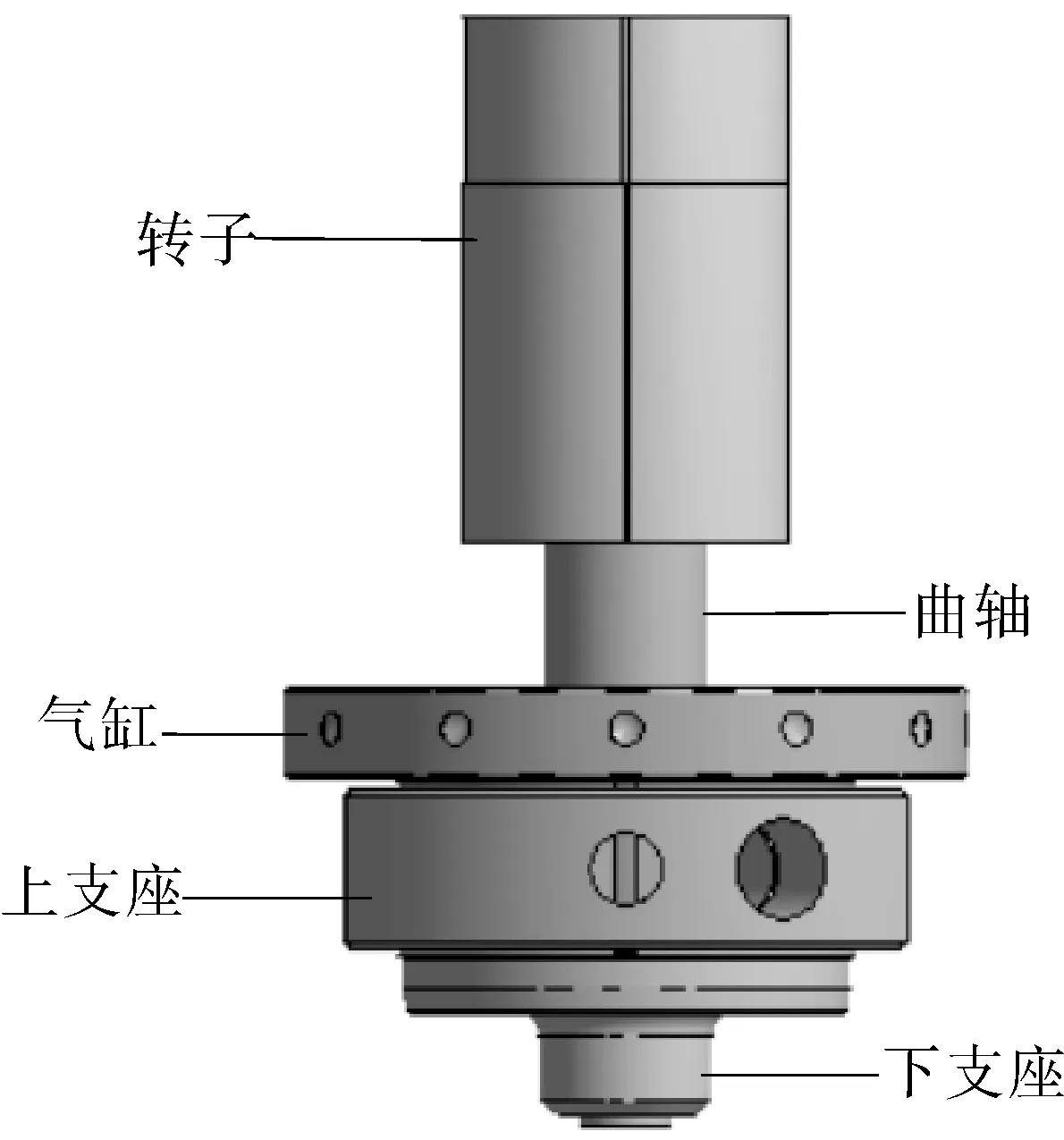
图4 转子-泵浦系统

本文采用SolidWorks 软件建立泵浦三维实体模型。将模型导入Ansys workbench 中，设定材料。采用软件自带的自动划分网格，按照实际受力方向添加结构载荷F，大小为4 700 N，设定方向沿x轴，按照实际三点焊接方式添加约束，约束点为上支撑座上面的A 点、B 点、C 点3 点，模拟实际焊点位置如图5 所示。经过计算输出结果如图6 所示，最大变形量为0.396 86 mm，并且最大形变位置在转子顶部，方向与力的方向相同，转子向下移动5 mm 后，有限元计算结果输出结果如图7 所示，最大型变量为0.36 mm，最大形变位置依旧在转子顶部，但是最大形变量得到改善。

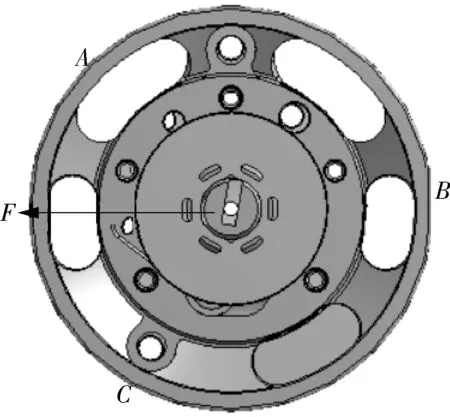
图5 约束与载荷示意

图6 原位置形变量

图7 转子下降后形变量

4 压缩机能效验证对比

经过理论计算与模拟分析后，新组装的压缩机需要进行单体能效验证对比，以保证新组装压缩机的性能不会受过多影响。

设计对照试验，1 台作为对照组，使用原设计压缩机电机；另1 台作为试验组，采用改进后的电机结果见表4。

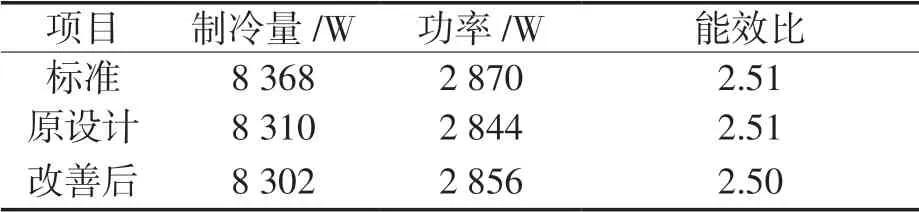
表4 压缩机主要性能对比

由表4 可以看出改善后的压缩机制冷量下降0.1%，功率增加0.43%，能效比降低0.55%。

5 结语

通过Ansoft Maxwell 分析，计算转子在原位置与下降后两种不同状态下与不同偏心距下的径向不平衡磁拉力。通过对比，转子的偏心量越大，产生的径向不平衡磁拉力越大；转子在向下移动5 mm 后，所受的径向不平衡磁拉力有所减小，并且与理论计算相符合。

采用Ansys workbench 软件分析转子强度，转子的变形量由之0.396 9 mm 下降到改善后的0.363 9 mm，减小8.3%。经过验证，压缩机主要性能不会因转子下降而产生明显影响。