类岩石蠕变性能试验及长期强度确定方法研究
张慎河徐学国王军杨景赵春鑫
(山东建筑大学 土木工程学院,山东 济南250101)
0 引言
地下工程围岩处于高应力状态下,极易受到临近巷道的开挖扰动影响,严重时会加速巷道变形破坏[1]。 高应力状态即长期强度应力状态下,当岩石所受应力处于该类岩石的长期强度以下时,岩石没有蠕变变形,采掘扰动对巷道变形影响极小;一旦应力超过岩石的长期强度,岩石蠕变变形增加,采掘扰动影响也会显著增加,反复扰动作用下巷道会加速变形甚至破坏[2-4]。 可见,岩石长期强度对岩石蠕变性能和蠕变扰动性能的影响较大,确定岩石的长期强度是非常必要的,但是岩石的长期强度具有时间效应,这些参数在岩石中非常难获取[5-7]。
王振等[8]对岩石进行常规单轴、常规三轴试验及单轴蠕变、三轴蠕变试验,提出了等应变速率曲线拐点法确定长期强度,并验证了极限应变法的准确性。 武东生等[9]通过比较灰岩在不同的蠕变方法下的试验结果,分析灰岩的蠕变力学性能,并改进稳态蠕变速率曲线法,得到了很好的验证效果。 崔旋等[10]研究岩石的应变变形理论,提出了黏塑性应变率法,这种方法可以缩短岩石蠕变时间,并验证了岩石长期强度的正确合理性。 崔希海等[11]通过比较岩石的横向蠕变与轴向蠕变的变化情况,得出了用岩石的横向蠕变确定的长期强度比轴向蠕变的阈值确定的长期强度低19%~35%,对工程设计与施工具有一定的指导意义。 此外,有更多学者对岩石的蠕变现象进行了研究[12-15]。
上述对岩石长期强度的确定方法大多集中在传统蠕变法或在传统蠕变法的基础上进行修正,岩石长期强度的确定仍然需要进行大量试验研究。 文章基于TAW-1000D 岩石三轴蠕变扰动试验仪,对类岩石试件进行了单轴蠕变性能试验,并对岩石蠕变力学性能进行分析,然后结合蠕变本构模型,推导出了可以预估长期强度的方程式,基于该方程式,通过瞬时单轴压缩试验确定岩石基本参数,将基本参数代入方程式后即可确定长期强度的范围值。
1 类岩石蠕变性能试验研究
1.1 材料与方法
1.1.1 室内试件制作
由于岩石是非均质的天然材料,即使是在同一块岩块上取出的岩芯,其离散性也特别大,而且岩石的取芯率极低,获得完整的岩芯较为困难。 针对以上问题,采用类岩石模拟砂岩。 根据相似模拟定理中的第三核心定理,凡具有同一特性的现象,若单值条件(容重、应力、应变、密度等条件)彼此相似,则由这些相似单值条件组成的现象也必定相似[16-17]。试验原型砂岩取自山东省泰安市华丰煤矿第11 煤层顶板,对其进行标准单轴抗压强度试验后获得基本物理参数,之后根据物理参数进行类岩石试件制作。 类岩石试件尺寸为Φ50 mm×100 mm,由铁铝酸水泥、砂和水按照一定质量混合制作而成,并将其放置在混凝土养护箱内养护20 d。 为了保证类岩石两端的不垂直度与不平整度均<0.02 mm,放到岩石打磨机上进行打磨,磨平端面,剔除带有肉眼可见缺陷(如裂隙,层理等)的类岩石试件。 最后使用HSYS4A 型岩石声波参数测试仪测试类岩石波速,剔除波速差别较大的试件。 最终获得20 块标准类岩石试件,如图1 所示,从中取8 块进行试验测试,并选取5 块进行单轴抗压强度测试,采用轴向变形加载方式,加载速率为0.1 mm/min。 绘制全应力—应变曲线,获得所需的基本参数。 岩石与类岩石基本参数见表1,全应力应变曲线如图2 所示。

图1 类岩石试件实物图

表1 岩石与类岩石基本力学参数表
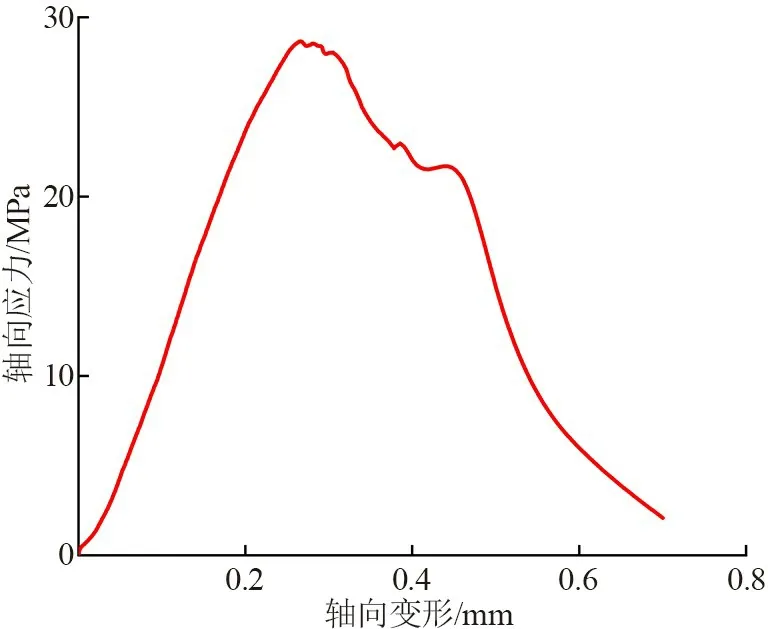
图2 类岩石全应力—应变曲线图
1.1.2 试验方案
采用TAW-1000D 岩石流变扰动试验仪进行类岩石蠕变试验研究,该试验仪由轴向加载系统、围压加载系统、扰动加载系统、数据采集系统共同组成,如图3 所示。 其中,轴向加载系统可施加轴向力为1 000 kN、围压加载系统可施加最大围压值为50 MPa、扰动加载系统最大扰动荷载值可以达到20 kN,以上各项精度均>99%。 数据采集系统可以自动记录应力、轴向应变、轴向应力、围压值、位移值、扰动载荷值和时间等数据。 类岩石试件属于软岩,蠕变性能明显,蠕变曲线较易获得,并且趋于稳定的时间较短,因此第一级荷载加载至单轴抗压极限强度的30%,分级加载荷载值为1 MPa(约为3.5%),各分级加载应力的间隔不低于2 h,且当蠕变曲线平稳变化时,可进行下一级加载。 待到试件发生破坏时,停止试验。

图3 岩石流变扰动试验仪实物图
1.2 蠕变性能分析
分别对3 个试件进行单轴蠕变性能试验,类岩石破坏形式属于劈裂破坏,如图4 所示。

图4 类岩石试件劈裂破坏图
经观察,编号7 ~9 的蠕变变形路径相似,对编号7 的试件进行蠕变结果分析,其全过程蠕变变形与相应的理想弹性材料比较曲线,如图5 所示。 其中,理想的弹性材料即材料受力只处于弹性阶段,无时间效应,变形与应力成正比,不会发生蠕变变形,完全符合胡克定律,由式(1)表示为

式中:ε为应变;σ为受到的应力,MPa;E为弹性模量,通过单轴抗压强度试验获取,MPa。
(1) 轴向蠕变曲线分析
由图5 中的全过程蠕变变形实验曲线可以看出,在每一级荷载加载后,都会产生一定的瞬时变形与蠕变变形,而且在岩石受到的应力中存在着一个阈值。 当应力小于这个应力阈值时,岩石处于第一蠕变阶段:蠕变变形衰减阶段;当应力超过这一应力阈值时,岩石进入第二阶段:等速蠕变阶段。 轴向蠕变变形较径向变形稳定,径向变形表现出的各个蠕变变形阶段较轴向蠕变变形阶段更敏感,这一现象对于深部岩石工程的支护设计及其稳定变形预测起到重要的指导作用[2]。
如图5(a)所示,类岩石受到的应力较小时,理想曲线明显低于试验蠕变曲线,试件初始加载所产生的瞬时变形大于理想弹性材料所产生的变形,这是由于在实际实验中存在压密阶段所导致,与类岩石的单轴抗压强度试验压密阶段产生的变形相对应。 继续进行分级加载,实验曲线与理想曲线变得较为接近,之后理想曲线明显高于实验曲线,类岩石的瞬时变形值逐渐增大,同时蠕变变形增大,类岩石的变形不再像之前那样稳定。 可以发现,类岩石受力在一定范围内时,实验曲线的瞬时变形与理想曲线的变形相比,随着应力水平的增加而降低,说明瞬时弹性模量发生了硬化。
(2) 径向变形曲线分析
如图5(b)所示,类岩石在开始受到较小的力,直接进入衰减蠕变阶段,并且理想曲线明显高于试验曲线,直到类岩石由衰减蠕变曲线进入等速蠕变曲线,瞬时径向变形大幅度提高,且随着应力的增加越来越明显,最后类岩石径向变形曲线显著高于理想曲线,即试件的径向力学性质发生了损伤。
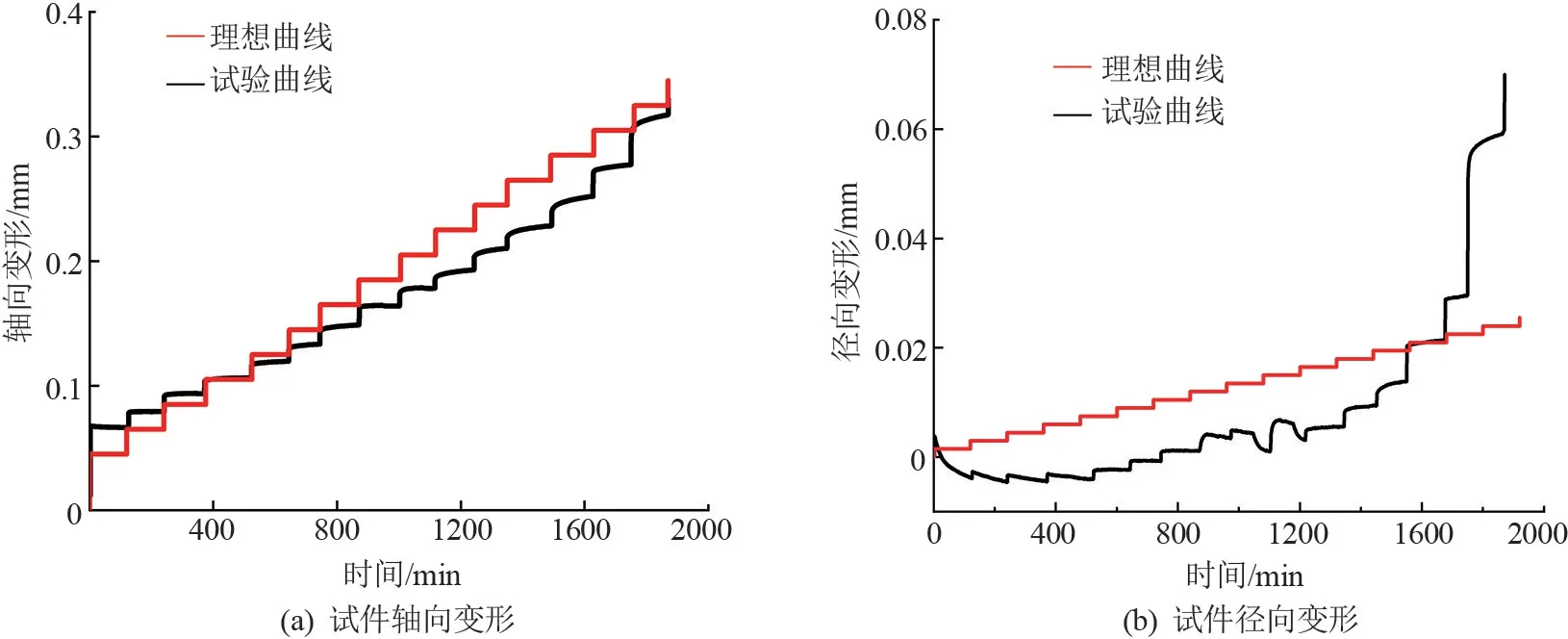
图5 试件全过程蠕变曲线与理想曲线比较图
1.3 类岩石长期强度确定
当试件受到的强度低于长期强度时,岩石的变形处于衰减蠕变阶段;当试件受到的强度高于长期强度时,岩石的变形处于等速蠕变阶段及加速蠕变阶段。 根据上述试验数据,为了更好的观察各级应力下的蠕变变形阶段,绘制出各应力下的蠕变变形曲线图,如图6 所示。
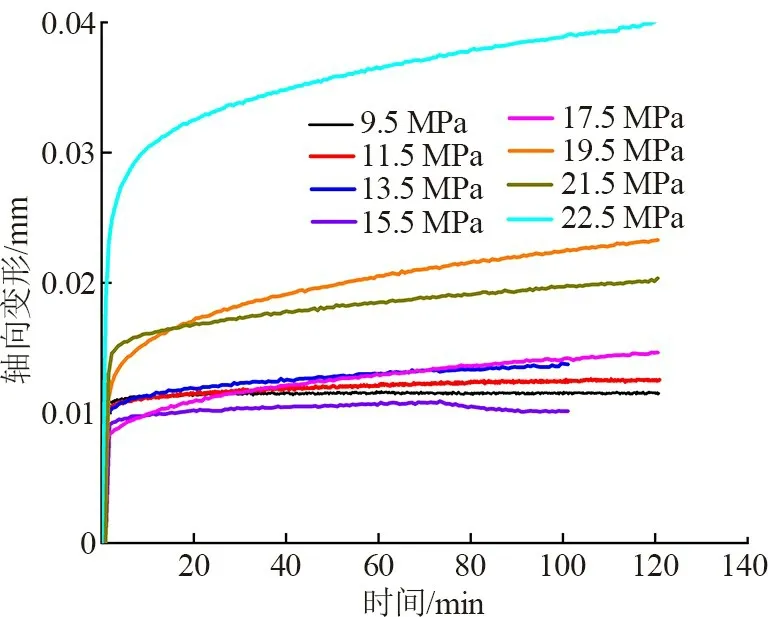
图6 各应力下变形曲线图
当类岩石受到的预静载为σc的33%、40%、47%和54%时,其相应的蠕变变形变化值分别为-8.85× 10-4、2. 755 × 10-3、2. 605 × 10-3和3. 2 ×10-3mm。 当类岩石受到的预静载为σc的61%、68%、75%和82%时,其相应的蠕变变形变形值分别为4.452×10-3、8.195×10-3、2.146×10-2和2.1755×10-2mm。 在受力为σc的33%~54%时,类岩石的瞬时变形值减小,同时与预静载为σc的68%~82%相比,蠕变变形较小,对应力的敏感程度也小。 当受力为σc的68%~82%时,类岩石的瞬时变形值随着应力的增大逐渐增大,表明类岩石已发生了损伤,且蠕变变形值随着应力的增大而大幅度增大,表明类岩石在受到较大的应力后,其蠕变特性变得更加突出,对应力更加敏感。 因此实际工程应将其受力控制在长期强度以下,由图6 可以看出,当类岩石受到的应力为15.5 MPa 时,其蠕变变形曲线较为平稳,最后出现轻微的衰减,表明处于衰减蠕变阶段;当类岩石受到的应力为17.5 MPa 时,其蠕变变形曲线处于匀速增长状态,表明处于等速蠕变阶段,故类岩石的长期强度为15.5~17.5 MPa。
2 长期强度理论分析及其验证
确定岩石长期强度的方法一般包括过渡蠕变法、等时曲线法、蠕变曲线与应力应变曲线结合法等[8,18]。 文章结合三参量模型的变形公式[19],推导出可以预估长期强度的关系式。 由以上试验可以得出,当岩石压缩强度低于长期强度时,不会发生蠕变破坏;当岩石的压缩强度等于长期强度时,所产生的瞬时变形与蠕变变形发生之和,称为稳定变形阈值εs。 若对岩石进行瞬时单轴压缩试验,受到的应力低于屈服强度σy时,岩石变形基本上为稳定变形;当岩石受到的应力高于屈服强度σy时,岩石将发生不稳定变形,岩石在屈服强度下发生的变形称为损伤变形阈值εy,具体的公式推导见式(2)~(8)。
三参量模型变形公式由式(2)表示为
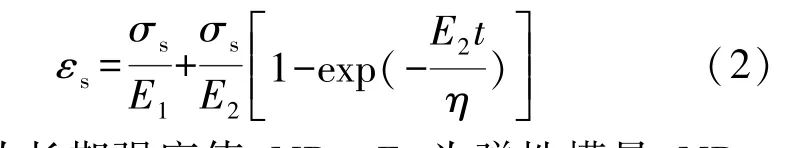
式中:σs为长期强度值,MPa;E1为弹性模量,MPa;E2为黏弹性模量,MPa;η为黏质系数。
式(2)中t→∞时由式(3)表示为

瞬时单轴抗压强度损伤变形阈值εy由式(4)表示为
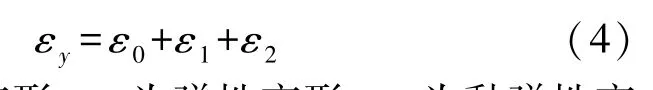
式中:ε1为压密变形;ε2为弹性变形;ε3为黏弹性变形。
由压缩试验值可知,岩石进行压密后,对岩石卸压,岩石的压密变形不再恢复。 因此,屈服应力σy主要由弹性阶段的应力σ1与黏塑性阶段应力σ2组成,由式(5)表示为
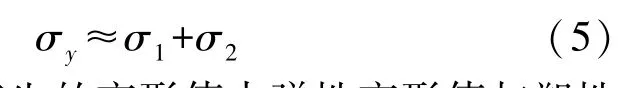
设弹性阶段产生的变形值占弹性变形值与塑性变形值之和的比例为x,则塑性变形占比为1-x。 将x带入式(5),屈服应力σy由式(6)表示为
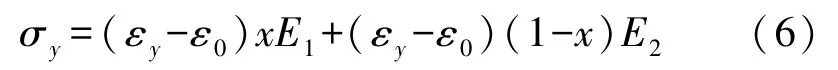
简化式(6)可得损伤变形阈值εy,由式(7)表示为
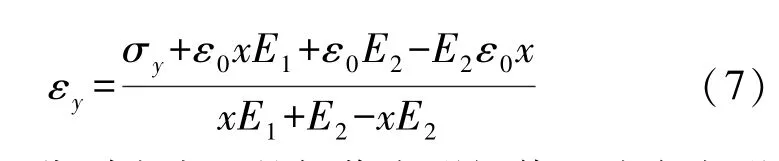
式中:εy、εs分别为岩石的损伤变形阈值和稳定变形阈值,两者之间存在着某种特定的关系,假定εs=Kεy,其中K为损伤变形阈值与稳定变形阈值的关系系数。 结合式(3)与(7),可以推导出预估长期强度的关系式,由式(8)表示为
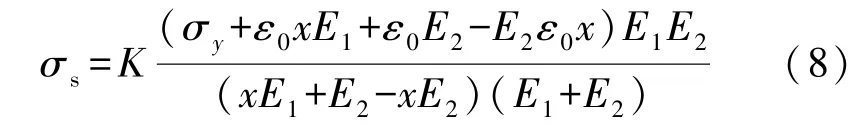
由式(8)可以得出,已知屈服强度σy、比例值x、压密变形弹性模量E1、黏弹性模量E2及关系系数K值,就可以预估长期强度值。 其中除K外,其余参数都可以通过瞬时压缩试验获取,K值需要进行大量的瞬时试验与蠕变试验,由试验结果总结得出。
对长期强度值进行验证,其中相应的参数由单轴抗压强度可以得出:σy=24.95 MPa、x=0.691、
ε0=0.021385 mm、E2=10.25 GPa。
对于K值的取值,尚需大量试验验证后获取,获取方法为:通过对岩石试件进行多组瞬时压缩实验,记录每组的损伤变形阈值εy,并且通过对相同岩石试件进行多组蠕变压缩实验,记录每组的稳定变形阈值εs,总结出两者之间的相关系数K。 此处暂取K=1,经计算可得σs=13.40 MPa,理论计算结果与实测实际长期强度有一定的偏差,处于保守范围,主要原因如下:
(1) 类岩石试件存在离散性问题。 与岩石相比,虽然在一定程度上降低了离散性,但是无法完全消除其离散性,做蠕变试验的类岩石试件的强度比之前做单轴抗压强度试验的类岩石试件强度大。
(2) 类岩石的基本参数的获取存在一定的误差。 此公式的参数主要由弹性模量、黏弹性模量和屈服强度组成,其中类岩石的基本参数物理量不能非常准确的获取,然而其中的任何参数出现误差,其结果就会出现误差。
(3) 假定的长期强度所产生的最终蠕变变形值εs与屈服应力εy所产生的变形值相等,即K=1,此假定存在一定的误差,K值的确定尚需大量的试验研究。
综上分析,利用式(7)所得的理论结果与试验结果有明确的相关性,可以在一定程度上预估岩石的长期强度,对工程的安全支护与长期强度的确定起指导作用。
3 结论
通过上述对蠕变试验结果的分析,可以得出以下结论:
(1) 单轴蠕变试验时,应力使岩石的性质发生变化,受力在长期强度以下时,其蠕变变形对应力不敏感,同时瞬时弹性模量发生硬化,瞬时变形值逐渐减小。
(2) 当类岩石受力高于长期强度值时,蠕变变形增加,蠕变变形对应力越来越敏感,瞬时变形值也随应力增加而增加,且蠕变性质十分突出,蠕变变形不稳定。
(3) 径向变形曲线与轴向变形曲线对比表明,径向变形对应力的敏感程度明显高于轴向变形对应力的敏感程度。

