基于上证50ETF期权的“定价核之谜”研究
(东北财经大学应用金融与行为科学学院,辽宁 大连 116025)
一、引言
定价核(Pricing Kernel)又被称为随机折现因子(Stochastic Discount Factor),自被提出以来在资产定价领域具有极其重要的地位(Lucas,1978)[18],是构成资产定价大厦不可或缺的一块基石。通过求解定价核,可以将所有资产定价理论纳入一个一般化模型,进而为所有金融资产定价。同时,定价核包含了投资者在不同状态下效用评估的重要信息,通过研究定价核可以反映投资者对市场未来不同情况的预期。
在理性投资者与完全市场等基本假设下,Dybvig(1988)[11]理论上证明了定价核是经济总财富的单调递减函数。但Ait-Sahalia and Lo(1998)[1],Jackwerth(2000)[17]及Rosenberg and Engle(2002)[20]基于美国市场数据的经验研究表明,定价核具有局部增加的特性,经验证据与理论结果相悖。这一现象后来被称为“定价核之谜”(Pricing Kernel Puzzle)(Brown and Jackwerth, 2012)[6]。随后,诸多学者采用不同金融市场的数据与不同方法证实了“定价核之谜”的存在,其中对美国金融市场的研究占绝大多数(Beare and Schmidt,2014;Cuesdeanu et al., 2017;Bali et al., 2017)[4][10][2],对德国市场与香港市场同样有学者给出了“定价核之谜”存在的经验证据(Golubev et al.,2014;吴鑫育,2015)[13][23];另外,也有学者认为如果对投资者效用函数的形式进行限制,“定价核之谜”就不存在(Chernov and Ghysels, 2000)[9]。
尽管现有文献对于境外主要发达市场的定价核均有研究,但对国内市场定价核的研究几乎为零。中国市场是股票市值排名第二的大市场,在国际金融市场中的地位与影响愈发重要,因此给出“定价核之谜”在中国市场是否存在的实证证据,对我国资产定价领域的研究具有极其重要的意义。同时,鉴于中国金融市场与发达金融市场在投资者与制度等方面存在诸多差异,如能给出“定价核之谜”在中国存在的经验证据,将会进一步为“定价核之谜”提供实证支持。
在“定价核之谜”被大量经验研究证实存在后,有学者研究了“定价核之谜”的形成原因。如果金融市场不能满足市场完整、投资者风险厌恶且具有一致的正确信念,就可能出现“定价核之谜”(Hens and Reichlin,2012)[15],另外有学者认为波动率可能是导致“定价核之谜”的原因(Song and Xiu,2016;Giacomini et al., 2008;Grith et al., 2013)[21][12][14]。不难发现“定价核之谜”包含了市场中一些隐藏的重要信息,但鲜有文献着眼于“定价核之谜”与市场表现之间存在何种关系。本文在对“定价核之谜”与市场走势的特征事实进行观察后,发现两者之间确实存在一定相关性,提出猜想“当期出现定价核之谜会预示下期市场出现震荡或下跌”,随后将Hens and Reichlin(2012)[15]的研究结果与“定价核之谜”成因会对市场造成影响的实证证据(郑振龙和孙清泉,2013;陈国进和张贻军,2009)[24][22]相结合,给出了猜想成立的理论支持,最后通过计量方法证实了上述猜想。
总的来说,本文首先选取上证50ETF日度收盘价来计算客观风险概率密度,并根据上证50ETF期权计算风险中性概率密度,求解得到经验定价核。随后对中国市场是否存在“定价核之谜”进行检验,根据Beare and Schmidt(2014)[4]的统计框架,本文构建了定价核单调性统计量,对所有月份的定价核进行统计检验。结果表明,在95%的置信水平下,可以在18%的月份1里拒绝定价核单调递减,即存在“定价核之谜”。最后,本文对定价核与上证50ETF走势之间的关系进行了分析,结果显示,“定价核之谜”与下期市场收益率呈反向关系、与下期市场振幅呈正向关系。
本文的主要贡献有以下两点:第一,首次给出了“定价核之谜”在中国金融市场存在的经验证据;第二,创新性地将“定价核之谜”与下期市场走势联系起来,在给出两者之间具有相关性的理论支持后,通过实证检验证实了“定价核之谜”对未来市场走势有一定的预测作用。
二、研究方法
(一)定价核的测算
通过对现有文献进行梳理,可以将定价核的估算方法大致分为两类。第一类方法是从计量经济学的角度进行研究,将定价核看作是所有个体禀赋聚合成一个整体的函数进行求解,其中具有代表性的例子为Chapman(1997)[8]等人的研究。第二类方法基于无套利原则,从资产定价的视角对定价核进行估算,其中具有代表性的例子为Rosenberg and Engle(2002)[20]、Beare and Schmidt(2014)[4]等人的研究。由于第一类方法中所需的总消费数据需要运用宏观经济数据来计算,而宏观数据的测量误差较大,因此定价核的估计存在较大误差。所以本文采取第二类方法,采用Monteiro et al.(2008)[19]提出的三次样条模型近似得到风险中性密度函数。该方法兼具灵活和参数化的优点,可以很好地拟合风险中性概率密度,进而计算得到定价核。
从定价核的基本表达式出发,若Yt为t期资产Y的价格,zt+1为t+1期资产的支付,Mt为当期定价核,则资产Y的定价公式如式(1)所示:

求解定价核的核心思想为“同一资产在不同概率测度下计算出的价格应当一致”。现考虑一个在t时期发行的或有要求权资产(如指数期权),其在t+1期的支付为zt+1=ft(xt+1),ft为标的指数的支付函数,xt+1为t+1期指数收益率。那么在风险中性概率测度Q下,该种资产在t期的价格为:

式(2)中的qt为该期关于标的指数收益率的风险中性概率密度(risk-neutral density),rt为当期无风险利率。
在客观概率测度P下,由期望的迭代法则可推得该种资产在t期的价格为:
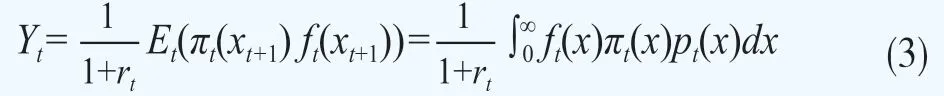
式(3)中的pt为该期关于标的指数收益率的客观概率密度(physical density),πt为剥离了无风险折现率的定价核(在本文以下部分所指定价核均为πt形式)。将式(2)与式(3)联立,即可得到定价核πt的表达式(4),在下面本文将分别给出pt和qt的计算方法。

1.客观概率密度pt的计算
本文参照Rosenberg and Engle(2002)[20]的方法对客观概率密度pt进行求解,具体步骤如下:
首先,对于使用标的指数数据描述股票指数收益时间序列变化过程,本文使用具有经验新息密度(empirical innovation density)的GARCH模型,模型的具体形式如下:
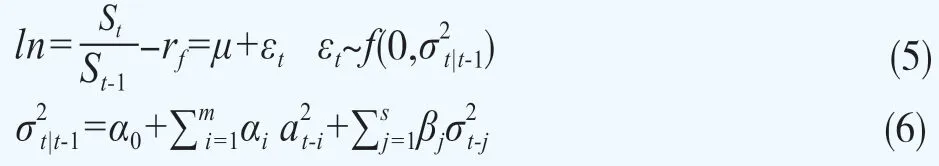
其次,在估计得到GARCH模型的参数后,通过将新息密度分解为时变和恒定的部分来模拟经验新息密度f。定义“标准化新息”为收益率新息εt与其条件标准差σt|t-1的比率,标准化新息密度(εt/σt|t-1)——即标准化新息集合——是经验新息密度的恒定成分。条件标准差(σt|t-1)是经验新息密度的时变分量。计算出的标准化新息的集合构成了经验密度函数,它可以体现出在实际金融市场中出现的过度偏斜、峰度和其他不能在正态分布下体现的特征。
最后,通过模特卡罗方法模拟整个周期收益率路径来求解客观概率分布。在根据单周期的模拟方法得到当期收益率与收益率新息εt+1后更新条件方差σt+2|t+1,进而得到第二个周期的回归新息εt+2,随后再更新条件方差σt+3|t+2,…,直至最后一期,最终得到多期对数收益率模拟值∑n i=1(μ+rf+εt+i)与多周期简单回报的模拟值{exp[∑ni=1(μ+rf+εt+i)]-1}。重复此步骤20,000次,得到整个周期的客观概率分布。
2.风险中性概率密度qt的计算
通常,对风险中性概率密度的计算可分为以下三种方法:(1)第一种方法对标的资产价格的变动模式进行了较强的假设,随后使用数值方法求解风险中性概率密度(吴鑫育,2015)[23];(2)使用非参数方法估计风险中性概率密度Q(Ait-Sahalia and Lo, 1998)[1];(3)首先对风险中性概率密度的分布进行设定,随后通过参数化的方法对其进行求解(Rosenberg and Engle,2002;Beare and Schmidt,2014)[20][4]。本文在第三种方法的基础上,依据Monteiro et al.(2008)[19]的方法使用三次样条近似风险中性密度函数。该方法在汲取前两种方法优点的同时,规避了他们的缺点,使结果兼具参数化与灵活性。
首先,构建三次样条风险中性密度的表达式,设风险中性密度q是在区间(x0,xk]上具有k个子区间与k+1个固定节点的三次样条(即平滑的分段三次多项式)。节点的选择是任意的,本文根据当期的条件波动率来选择结点的位置与个数,具体做法详见实证部分。给定节点的位置后,q可以写成式(7)的形式。
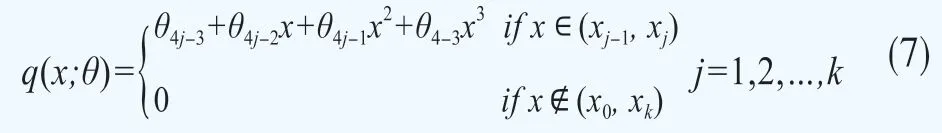
同时q(x;θ)需要满足如下条件:(1)概率密度函数q在整个区间积分要求等于1;(2)函数在各个端点处连续且二次可导;(3)函数在左右端点x0和xk处连续并且等于零;(4)函数在区间内为非负函数。
其次,求得使以交易量vi加权的市场价格wi与用风险中性密度q拟合的价格之差的平方和最小的最优参数θm,用交易量加权的做法源于高频交易资产更有可能反映出准确的定价。参数θm的表达式为
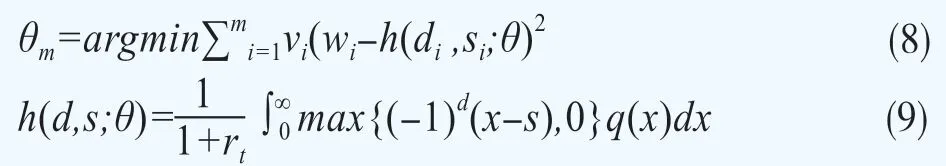
其中di为期权的行权方向,di=1为看涨,di=0为看跌;si为期权的行权价格;rt为当期的无风险利率。
最后,将估计出的参数θm代回风险中性密度q的表达式,估计完成。
(二)统计检验
本文按照Beare and Schmidt(2014)[4]的统计检验方法,通过计算序数优势曲线(Ordinal Dominance Curve)与最小凹面主函数(Least Concave Majorant)之间的距离构建检验统计量,对定价核的单调性进行统计检验。首先,建立原假设与备择假设:
H0:定价核是非增的
H1:定价核不是非增的
单调性检验方法的基本原理是基于定价核π的单调性与序数优势曲线的凹度之间的等价关系。首先对前文所得q与p进行积分,可获得对应的累计概率分布函数Q与P,设m表示当期观察到的期权合约数量,n表示时间序列的长度,将Qm和Pn作为Q和P的样本大小为m和n的无偏估计值。给定对Qm和Pn,本文构造相应的序数优势曲线ϕm,n:[0, 1]→[0, 1]如下:
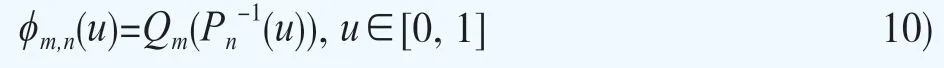
构造ϕm,n的最小凹度主函数Mϕm,n,该函数定义为最小的且处处大于等于ϕm,n(u)的凹函数。最后,通过Mϕm,n与ϕm,n之差的构建检验统计量来对原假设与备择假设进行检验:
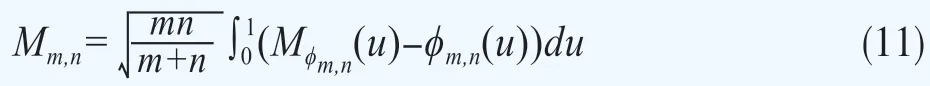
三、实证检验
(一)样本选取和变量定义
本文使用在上海证券交易所交易的上证50ETF期权数据估算风险中性概率密度,样本区间为2015年2月9日至2019年4月1日,共计118,146个期权合约的交易数据,数据来源于Wind资讯。在实证研究中,本文对样本数据进行了如下筛选:(1)剔除成交量为0的期权数据;(2)剔除在值程度小于0.85和大于1.15的看涨期权数据;(3)剔除在值程度大于1.15和小于0.85的看跌期权数据。经筛选后,获得满足条件的期权合约数量1025个。随后,从期权当日行情数据与合约标的数据中提取风险中性概率密度计算所需的d-行权方向、v-当日交易量、w-市场价格、s-行权价格,计算风险中性概率密度。
对于期权标的价格数据,本文选取2005年1月1日至2019年4月1日的上证50ETF后复权收盘价,用当日收盘价St除以前一日收盘价St-1取对数得到当日对数收益率,计算客观概率密度。
在后文验证定价核之谜与市场相关性时,本文用下期上证50ETF的对数收益率与振幅对衡量定价核之谜程度的定价核非单调递减统计量进行了回归,选取股市流动性指标与实现波动率作为控制变量,相关变量的含义和定义式如表1所示,上证50ETF数据与所选取回归变量均来源于Wind资讯。
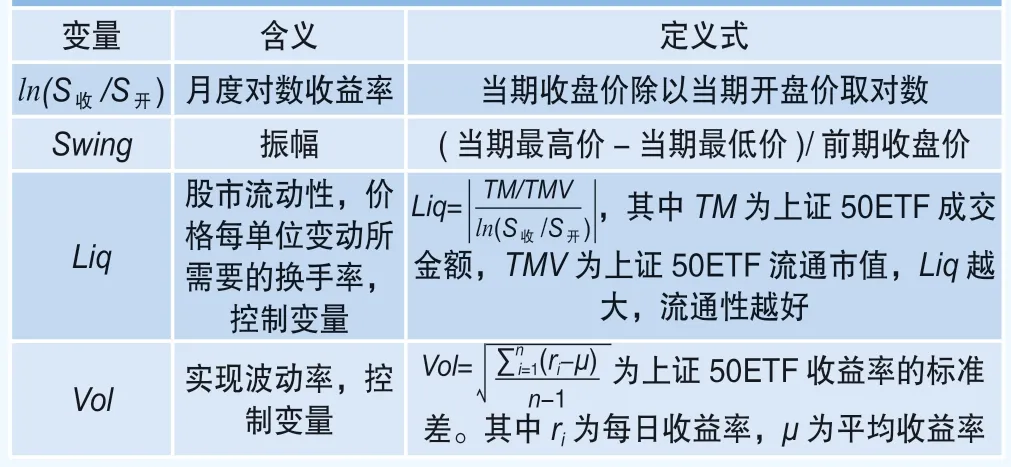
表1 变量的定义
(二)定价核计算结果
1.P测度的计算结果
本文采用经验概率分布的GARCH模型对上证50ETF的对数收益率序列进行建模,进一步应用蒙特卡洛模拟的方法模拟出未来一个月的客观概率密度。首先,采用ADF方法对上证50ETF对数收益率序列进行平稳性检验,结果表明上证50ETF对数收益率是平稳序列。其次,对均值方程的残差项进行分析,发现收益率残差的分布与正态分布并不匹配。最后,应用Ljung-Box混成检验方法对残差进行ARCH效应检验,结果发现各阶滞后项的p值都接近于0,认为残差的平方序列存在显著的自相关性,同时也说明序列存在很强的ARCH效应。
虽然残差并不满足正态分布的特征,但根据Bollerslev and Wooldridge(1992)[5]的研究结果,即使真正的新息密度是非正态的,使用正态假设的GARCH模型也能提供一致的参数估计。所以,本文采用标准的GARCH模型对收益率时间序列进行拟合,通过比较不同阶数的AIC与BIC值,本文最终采用GARCH(1, 1)模型,拟合结果如表2所示。
从表2的结果可以看出,均值方程中的系数接近0,条件波动率方程中前一期新息的系数为0.1,前一期条件标准差的系数为0.88,说明当期条件波动率确实与前一期相关,选择GARCH模型对收益率时间序列进行拟合是合理的。将条件标准差与标准化新息密度相乘,获得该期的经验概率分布。将符合经验概率分布的信息替换原有的正态分布新息,得到经验概率分布的GARCH模型:
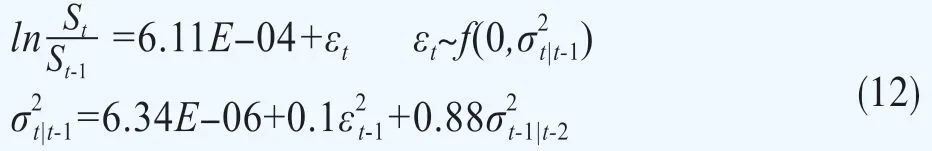
最后,本文运用经验概率分布的GARCH模型,在每个月的特定日期运用蒙特卡洛方法模拟未来一个月的对数收益率,并重复20,000次,进而获得基于估计日所能获得信息对一个月后客观概率密度曲线的估计。
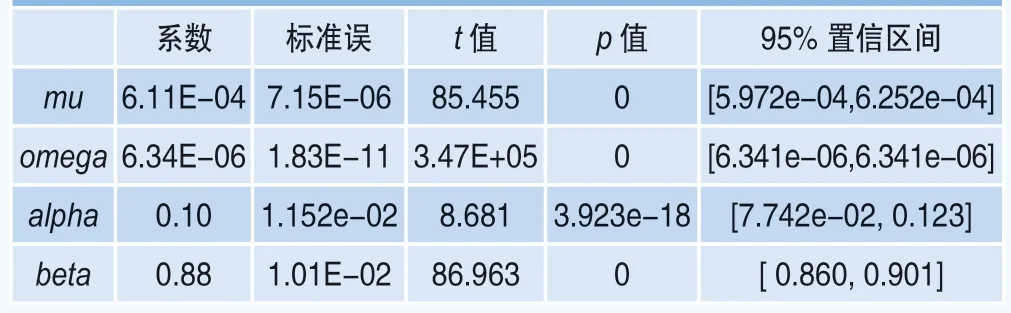
表2 上证50ETF对数收益率GARCH模型拟合结果
2.Q测度的计算结果
本部分采用风险中性概率密度的三次样条插值模型对上证50ETF期权的交易收盘价进行参数拟合,求得最优参数后代入模型,最终得到风险中性概率密度。基于前文对客观概率密度的估计,以下月到期日当日价格估计分布的条件标准差为基准,确定风险中性概率密度的最优区间与子区间。具体而言,本文按照式(13)确立节点的位置及个数,其中S0为估计当日的标的收盘价,a=[3.25 2.25 1.5 1 0.5 0]2。

本文采用Monteiro et al.(2008)[19]等人提供的一种基于半定规划的方法对参数θm进行求解,最后代入式(8)得到风险中性概率密度q。为对拟合结果进行检验,本文利用得到的风险中性概率密度曲线计算期权的拟合价格,并计算其与市场价格的偏离程度,误差为17.7%3,可认为拟合出的风险中性概率密度很好地提取了期权市场价格中所包含的信息。
3.实证定价核的计算结果
基于前文客观概率p与风险中性概率密度q的计算结果,对定价核进行求解。由于在市场的某些特殊时期投资者情绪过激,位于分布尾端的风险中性概率密度曲线与客观概率密度曲线差异过大,导致定价核出现指数型暴增,失去了实际意义,对于该种情况本文截取月涨跌幅在20%以内的范围对定价核进行求解,使得定价核的结果便于横向比较,更具实际意义。基于当月数据求解的下月定价核结果如图1所示(50期,2015年3月~2019年4月)。
对图1中定价核的形状进行直观观察可以发现,大部分定价核都呈现出单调递减的形式,个别月份的定价核呈现局部递增与U型定价核的情况,但是这一结论仅是直接观测出的,没有相关理论与数据支持,所以本文在下节进一步研究定价核的单调性,通过构建检验统计量,在统计层面上给出定价核之谜是否存在的结论。
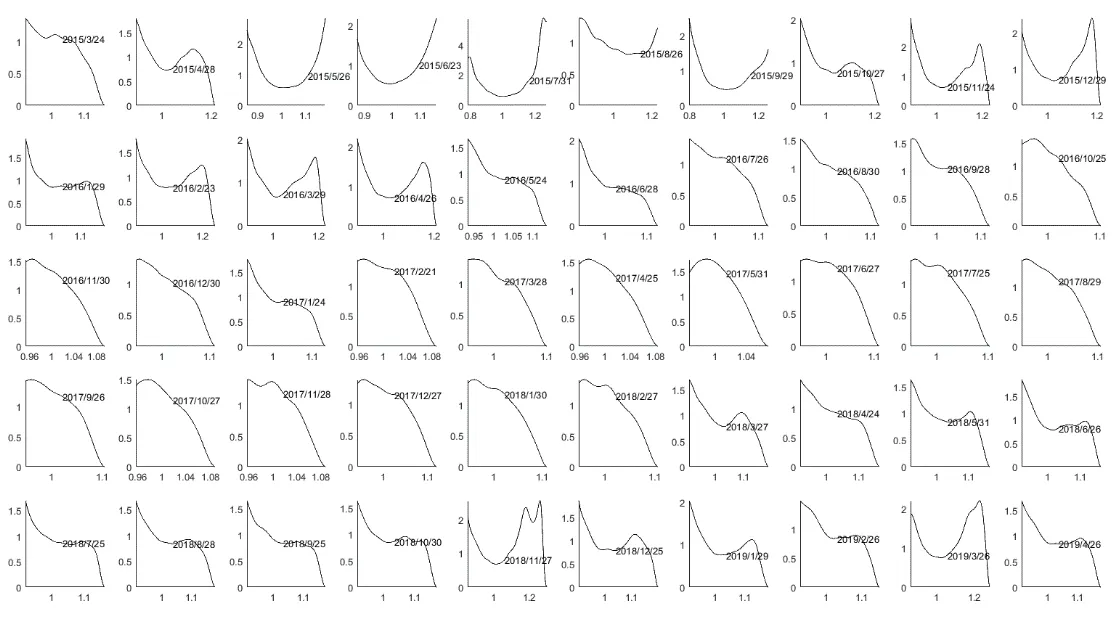
图1 实证定价核结果
(三)统计检验结果
基于本文研究方法(二)中的统计框架,本节首先求得每个定价核对应的序数优势曲线ϕm,n,在此基础上做出每条序数优势曲线ϕm,n对应的最小凹度主函数,结果如图2所示。
基于图2中两条曲线之差的积分,即图中的阴影部分,构建定价核非单调递减的统计量M如表3所示。
依据理论部分对临界值的计算方法,本文通过蒙特卡洛模拟方法得到了检验统计量的临界值。在95%的置信度下,拒绝值为0.063。根据结果,在95%的置信度下,整个时间区间内18%月份的定价核是非单调递减的,即存在“定价核之谜”。
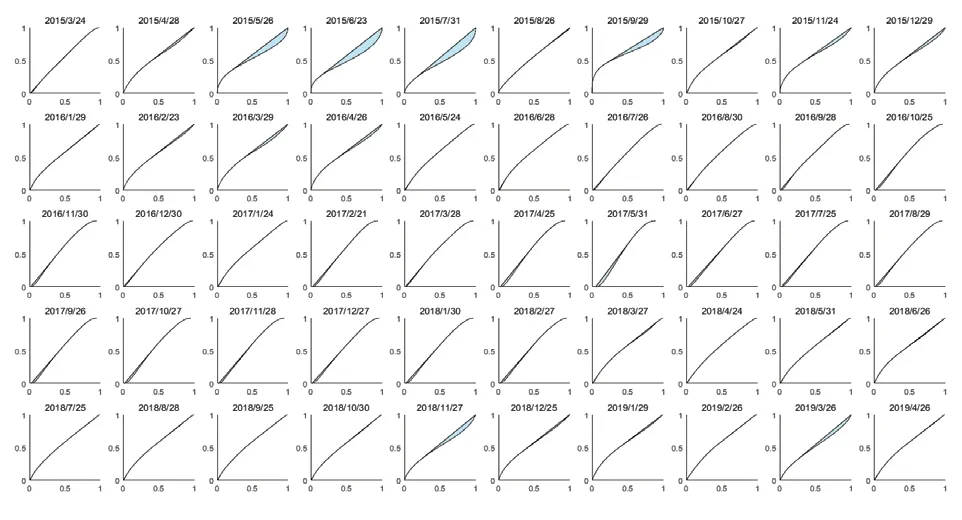
图2 序数优势曲线与最小凹度主函数
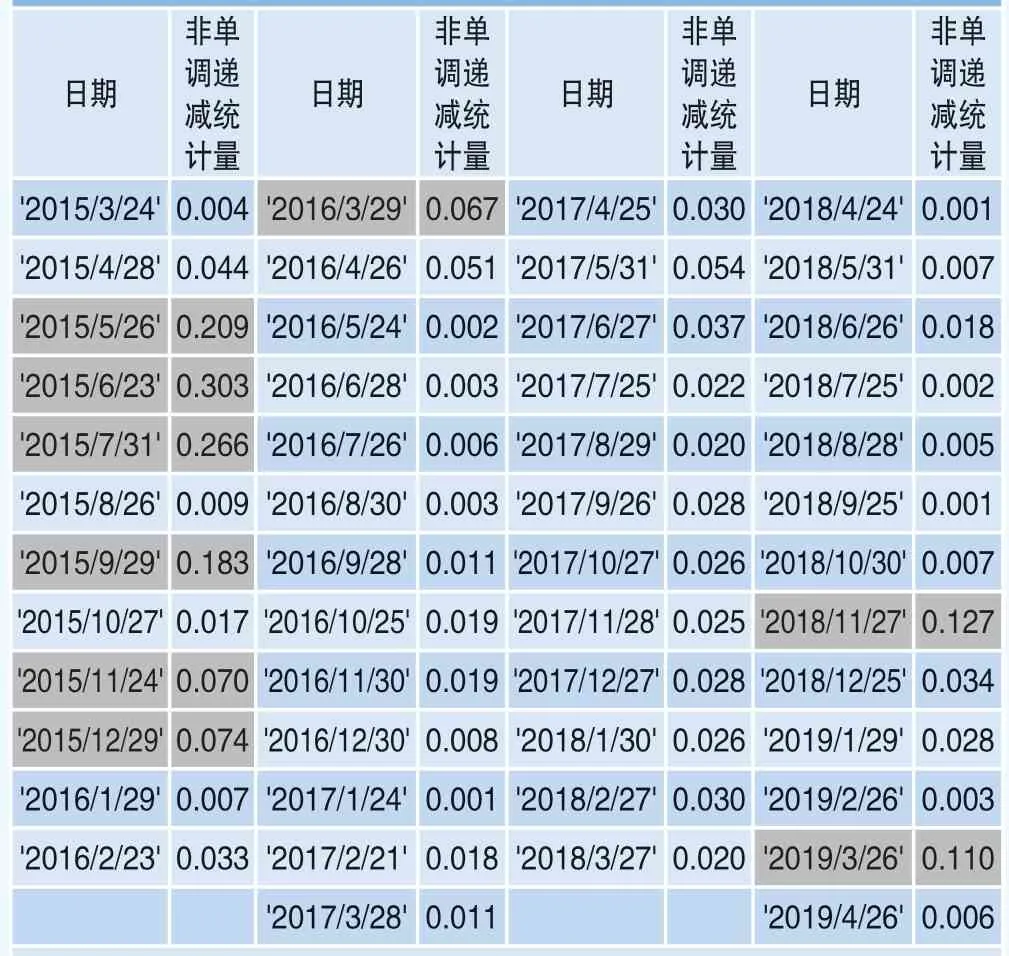
表3 月度定价核非单调递减统计量
四、进一步研究
(一)“定价核之谜”与市场走势相关性的特征事实与猜想的提出
为进一步研究“定价核之谜”,本文将估算得到的定价核时间序列与市场走势放在一起进行对比,对两者之间的相关性进行分析。首先,本文对上证指数从2015年初到2019年中的走势进行了总结。通过对比指数走势与定价核的时间序列,发现当定价核呈现出较大程度的U型或局部递增程度很大(即定价核的非单调性异常显著)时,下月市场往往会出现不同程度的大幅下跌或震荡,如表4所示。
基于以上事例,本文提出如下猜想:“定价核之谜”的出现往往预示着下期市场将出现大幅下跌或震荡。为验证这一猜想是否合理并具有一般性,下面本文将给出该猜想的理论支持,并用下期上证50ETTF对数收益率与振幅对能够衡量“定价核之谜”程度的定价核非单调递减统计量进行回归,进行实证检验。
(二)猜想的相关理论支持
根据Hens and Reichlin(2012)[15]的理论推导,“投资者的风险寻求行为”(高估尾部事件概率)与“不完全市场和异质信念”导致的定价核中递增部分,可能是导致“定价核之谜”的潜在原因。进一步,本文将分析导致定价核之谜潜在原因与市场走势之间存在何种相关性。
1.“投资者的风险寻求行为”(高估尾部事件概率)与市场收益之间的关系
Brunnermeier et al.(2007)[7]指出过度自信会使投资者的主观概率偏离客观概率,过于重视尾部事件发生的概率。Barberis and Huang(2008)[3]在前景理论的基础上,认为投资者会对资产收益分布的两端赋予较高的概率权重。这些研究都表明投资者存在高估极端事件概率的心理,持有彩票类股票能提高其预期效用,并愿为彩票类股票支付较高的价格,从而导致赌博偏好的风险收益为负。郑振龙和孙清泉(2013)[24]选用Fama-French三因子模型作为基准定价模型来考察中国股市中彩票类股票组合的相对收益表现,结果表明,与“非彩票类股票”和“其他股票”相比,在我国股市上投资“彩票类股票”的相对收益为负且显著。综上,在中国市场投资者高估尾部事件概率这一特征与风险回报呈负相关系。
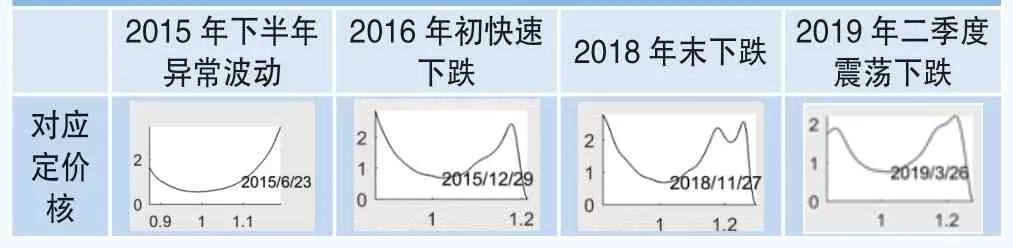
表4 2015年至今大幅震荡或下跌时期对应定价核
2.“不完整的市场和异质信念”与市场收益之间的关系
Hong and Stein(2003)[16]根据行为金融理论的框架,认为投资者的过度自信会导致异质信念的产生,并从投资者具有异质信念与市场存在卖空限制这两个角度,论证了暴跌的产生原因,以及暴跌为什么具有传染性。由他们的理论模型分析可知,在市场存在卖空限制的背景下,投资者的异质信念会导致坏信息不能及时被投资者知晓,从而造成大范围的暴跌。陈国进和张贻军(2009)[22]基于中国股票市场对异质信念、卖空限制与股价行为进行了研究,结果表明,异质信念与不完全市场的存在会导致市场会出现暴涨暴跌、大幅震荡,且暴跌的影响更大。
由此,无论导致定价核之谜的成因是“投资者高估尾部概率”还是“不完整的市场和异质信念”,本文都找到了其与市场收益负相关并会导致市场震荡的证据,进而给出了“定价核之谜”会预期下期市场出现震荡或下跌的理论支持。
(三)猜想的实证检验结果
为给出猜想的实证检验结果,本文首先关注“定价核之谜”对下期市场收益率的影响,用下一期的对数收益率对当期定价核非单调递减统计量进行回归。为样本匹配,被解释变量使用t+1期,解释变量使用t期,控制变量使用t期,其中式(15)为在式(14)的基础上添加了实现波动率与流动性指标两个控制变量。
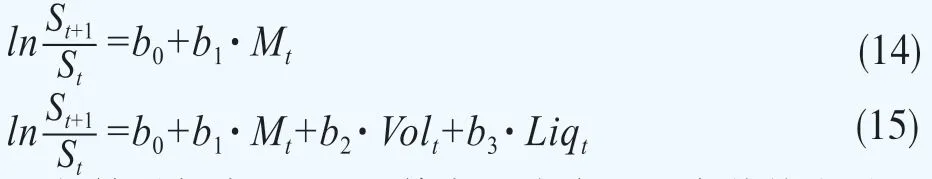
回归结果如表5所示,其中Mt为衡量“定价核之谜”显著程度的统计量。
从方程(14)的回归结果可以看出,定价核非单调统计量的系数为-0.163且在1%显著性水平显著(t=-2.83),说明定价核的非单调递减统计量对下一期收益率有显著的负向影响;在方程(15)中,控制了波动率和流动性指标之后,定价核非单调递减统计量的系数在10%的显著性水平下依然为负(t=-1.72),这说明“定价核之谜”对下期市场收益率确实有负向影响,与本文的猜想一致。时间序列回归易产生“伪回归”问题,因此本文对回归的残差序列进行了ADF检验,检验结果表明方程(14)与方程(15)的ADF检验统计量分别为-8.1897与-8.2517,均小于1%显著性水平的Mackinnon临界值-3.435,因此残差序列是平稳的,上述回归结果不存在伪回归问题。
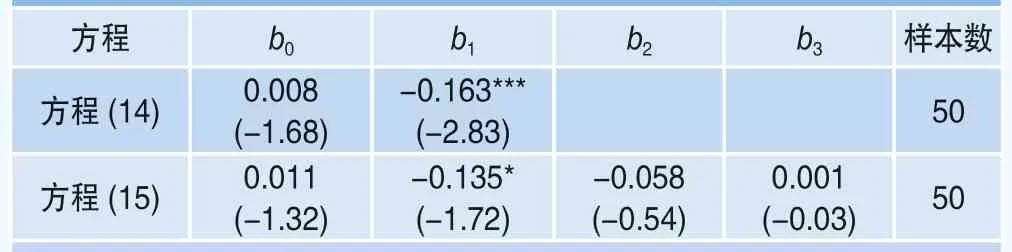
表5 当期定价核与下期市场收益率的回归结果
再用振幅对当期定价核非单调递减统计量进行回归,同样选择实现波动率与流动性指标作为控制变量,回归结果如表6所示。
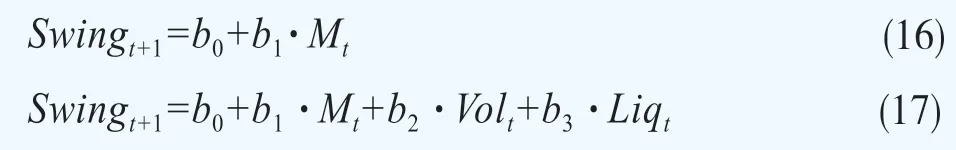
从方程(16)的回归结果可以看出,定价核非单调递减统计量的系数为0.619且在1%显著性水平下显著(t=5.78),说明定价核非单调递减性统计量对下一期振幅有显著的正向影响;在方程(17)中,控制了波动率和流动性之后,定价核非单调统计量的系数依然在1%显著性水平下为正(t=3.38),这说明“定价核之谜”对下期市场振幅确实有正向影响,与本文的猜想一致。同样对“伪回归”问题进行了检验,方程(16)与方程(17)残差的ADF检验统计量分别为-7.2802与-4.3386,均小于1%显著性水平的Mackinnon临界值-3.435,上述回归结果不存在伪回归问题。
综上,本文运用下期市场对数收益率与振幅对能够衡量定价核之谜的定价核非单调递减统计量分别进行了回归,结果表明定价核之谜的出现与下期市场收益率呈显著的负向关系,与下期市场振幅呈显著的正向关系,并且再加入了控制变量后依旧显著。这一实证结果证实了本文提出的猜想。
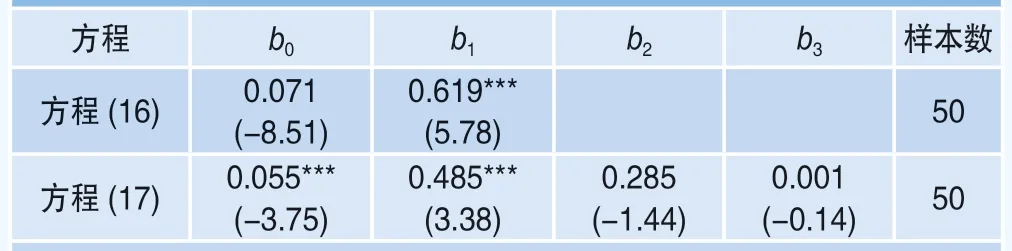
表6 当期定价核与下期市场振幅的回归结果
五、结论
本文首先利用具有经验概率分布新息的GARCH模型对上证50ETF对数收益率进行模拟来计算客观风险概率密度。接下来,利用GARCH模型得到的条件波动率确立风险中性概率分布的分布区间并构建三次样条插值的风险中性概率密度参数模型,利用市场上观测到的期权数据(交易量、行权方向、行权价格、收盘价格)对模型参数进行估计,代入原模型得到风险中性概率密度。将风险中性概率密度与客观概率密度相除,本文获得了中国市场的月度定价核。观察发现大部分时间定价核表现出了单调递减的形式,在某些特殊时期定价核呈现出了局部递增或U型的特征。随后,为更准确地检验“定价核之谜”,本文构建了单调性统计量,对所有月份的定价核进行单调性检验。结果表明,在95%的置信水平下,可以在18%的月份里拒绝定价核单调递减,从而首次给出了“定价核之谜”在中国市场存在的经验证据。最后,本文对定价核与上证50ETF走势之间的关系进行了分析,提出猜想——“定价核之谜”的出现往往预示着市场下期走势会出现震荡或下跌。为验证这一现象,本文用下期市场收益率、振幅对定价核非单调递减统计量进行了回归,结果表明非单调性统计量是显著的,“定价核之谜”与下期市场收益率呈反向关系、与下期市场振幅呈正向关系。
注释
1.根据投资者预期短时间内(一个月)不变的假定,本文选择对月度定价核进行计算。
2.a值的选取是任意的,实证结果表明按该a值划分区间计算得到的风险中性概率密度是最优的。
3.限于篇幅限制未给出期权拟合价格与实际市场价格误差的计算结果,如有需求,可向作者索要。

