方形截面弯管流量计计算模型建立与率定

刘斌云 赵嘉珩 任仲宇 谭九岑 王炳鑫

摘  要：利用量纲分析基本理论建立方形截面弯管流量计的理论计算模型，并对两类测压管方位角23°、45°及弯管曲率半径r分别为40mm、50mm、60mm的六种弯管流量计实验件进行室内过流实验，通过实验确定各种弯管流量计的流量理论计算模型待测系数。同时，通过实验获得了理论模型的计算精度。结果表明，各种管型弯管流量计按所建立的理论计算模型计算出的管内过流量都不同程度的接近于实测流量，而流量模型测算相对误差均值的大小与流量计上所布设测压管的方位角大小及弯管曲率半径的取值大小有关。实验结果分析还表明，曲率与水力半径比值r/R相对较大、方位角相对较小的管型5流量计的设计参数相对最优，其计算误差最小。

关键词：计量学  方形截面  弯管流量计  流量系数  理论模型  率定

中图分类号：TB92           文献标识码：A 文章编号：1674-098X（2020）07（c）-0053-04

Abstract： Based on the basic theory of dimensional analysis， the flow theoretical calculation model of square cross section elbow flowmeter is established， through-flow tests were carried out on six kinds of elbow flowmeter test pieces with azimuth angle 23°，45° and curvature radius r of 40mm， 50mm and 60mm， respectively， the measured coefficients of the theoretical calculation models of various elbow flow meters are determined by experiments，meanwhile， the calculation precision of the theoretical model is obtained. The results show that the flow rate calculated by the theoretical calculation model is close to the measured flow rate in different degrees， the mean value of the relative error of the flow model is related to the azimuth angle of the pressure tube and the curvature radius of the tube.The design parameters of tube-type 5 flowmeter with larger r/ R ratio and smaller azimuth angle are relatively optimal and its average calculation error is the least.

Key Words： Metrology;Square cross section;Elbow flow meter;Flow coefficient;Theoretical model;Calibration

弯管流量计的工程应用很广，针对其相关应用的问题研究也很多样。例如，实际工程应用中不同材料不同斜接角度弯管的流量测量精度问题，蒸汽计量中弯管流量计的巧用与相较孔板流量计的测量优势问题[1-2]。也有研究环境温度与弯管流量计直管段长对其计量的质量评价问题[3]，以及不同取压孔直径对弯管流量计流量系数影响及取压孔不同布设方位角对量程变换的影响问题[4]。弯管流量计也应用于气固两相流如煤粉质量流量的量测[5]。另外，研究电极安装平面位置对电磁弯管流量计的测量精度的影响以及如何提升流量计量程低端的差压测量精度方面近期也有研究成果[6-7]。然而，上面所涉及的研究对象弯管流量计都有一个共同的特点，即流量计的过流横断面均为圆形。而本文主要针对另一种横截面类型，即方形截面。事情缘于当时委托厂家加工一个曲率半径较小的圆形截面弯管流量计时碰到的加工精度困难所引起，当时厂家建议将弯管流量計横截面由圆形改成方形更方便于加工并提高制作精度。因此，此文主要涉及方形截面弯管流量计的理论量测模型研究，并结合实验实测数据确定模型流量系数相关性能参数，对不同测压孔方位角与不同曲率半径的方形截面弯管流量计的量测计算精度进行对比分析与最优模型率定。

1  方形截面弯管流量计计算模型

圆截面弯管流量计流量计算大多采用强制涡流理论流量公式：

其中α，r，d分别为流量系数，曲率半径及管内直径。对于方形截面，不能由圆形截面推导出来，需要重新建立其流量计算模型。设管内流量Q仅与方形弯管过流横截面的水力半径R、弯曲段曲率半径r、流体质量密度ρ以及测压管内外侧压强差?p有关，即函数表达式为：此式也可写成

其中过流横断面的水力半径R定义为过流横断面积与过流横断面的湿周（此处为周长）之比，对于方形截面，其水力半径R=（a×b）/（2a+2b），其中a，b分别为方形过流截面的宽与高。

由量纲分析法（π定理）原理[8]，选取参数R、ρ、Δp为基本物理量，即可写出两个无量纲π项：

其中α、β、γ为无量纲指数。由量纲和谐原理有：

其中长度L、质量M、时间T为三个基本量纲。按式（4）三个基本量纲的指数和两边相等，通过列方程组可解出：

由F（π1，π2）=0，可导出方形截面弯管流量计理论计算模型为（其中Δp=ρgΔh）：

Q=f（r/R），此式可变换为：

式中f1（r/R）是与无量纲数r/R有关的参数，为待测流量系数，Δh为弯管测压孔内外两侧的测压管水头差。

2  管型设计与实验方法

弯管流量计实验管型设计采用相同玻璃材质、不同曲率半径与不同取压孔管方位角组成的6种方形截面90°弯管流量计管型实验件进行室内实验。弯管部分内部过流横断面尺寸均采用宽高尺寸a×b为8mm×14mm的方形断面（R=28/11mm），通过弯管中心线的弯曲面曲率半径分别采用为r=40mm、50mm 、60mm，方位角θ分别采用23°与45°（具体制作尺寸图与实物件参见弯管流量计管型图1～6图及图7）。

实验台装置如图8所示，该装置为一台恒定总流伯努利方程综合型实验装置，上部玻璃水箱能提供0.6m恒定水头（装置下部装有自循环供水器）。水箱出流管道中间装有文丘里数显流量仪（精度0.5级），实验時利用量筒和秒表计算进行了人工校准，数显流量仪量程为000.0～999.9×10-6m3/s，实测流量均在量程范围内。

实验中将以上6种规格管型的方形弯管流量计连接于总流能量方程测流实验装置进行过流试验，记录各种管型通过不同过流流量时流量计上测压孔的测管读数h1、h2，并计算其Δh（Δh=h2-h1）值，并取其均值列于表中。利用各读数实验组均值确定所建立计算模型（7）式的率定待测系数f1（r/R）。

3  实验结果与分析

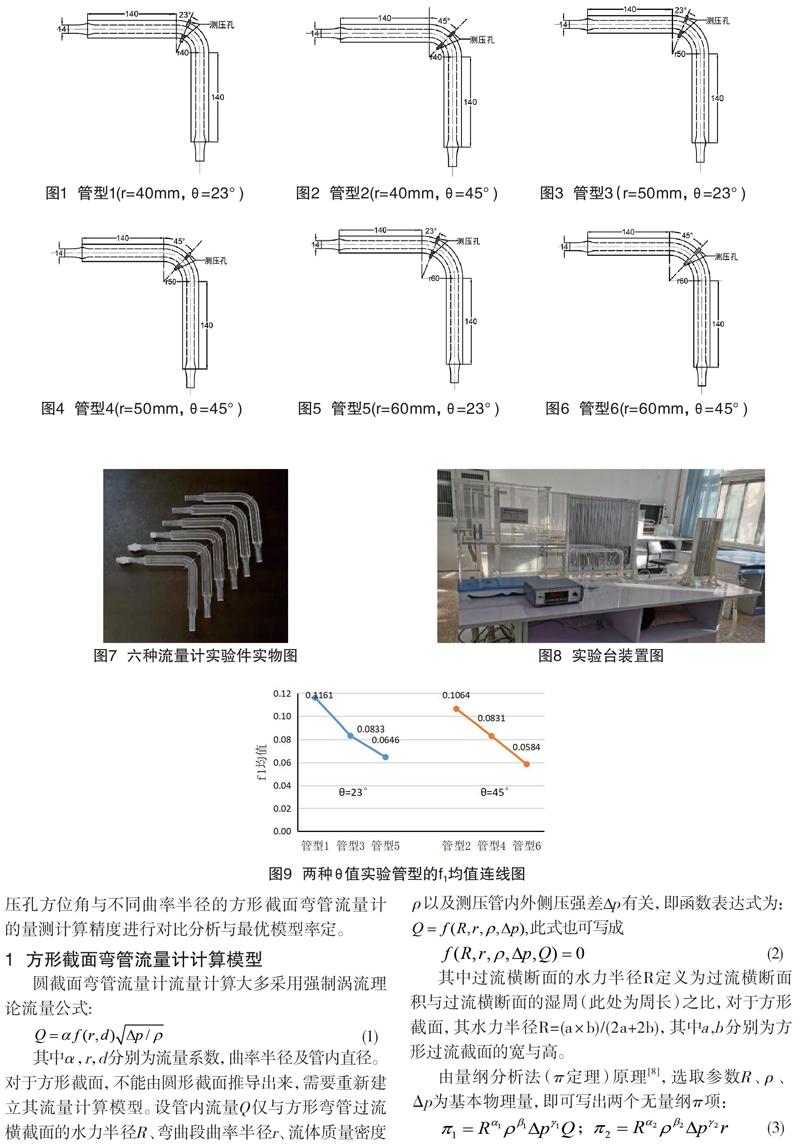
对六种管型弯管流量计实验件分别在4种不同流量下做过流实验。运用所建立的理论计算模型式（7），并结合实测流量Q实测与Δh的均值则可反推出各均值流量下的待测流量系数f1（r/R）值。实测流量均值与待测系数f1均值计算结果见表1，并将测定的各实验管型流量系数f1均值点连成曲线如图9所示。

对表1与图9连接曲线进行分析，可得出如下结果：首先，当方向角θ相同时，弯管流量计曲率半径r值越大，其流量系数f1均值则越小。其次，经计算得出θ为23°及45°时流量系数f1均值随r值的平均变化梯度分别为0.257%/mm与0.240%/mm。可见，流量计的方向角θ越小，其f1均值的平均变化梯度则越大。

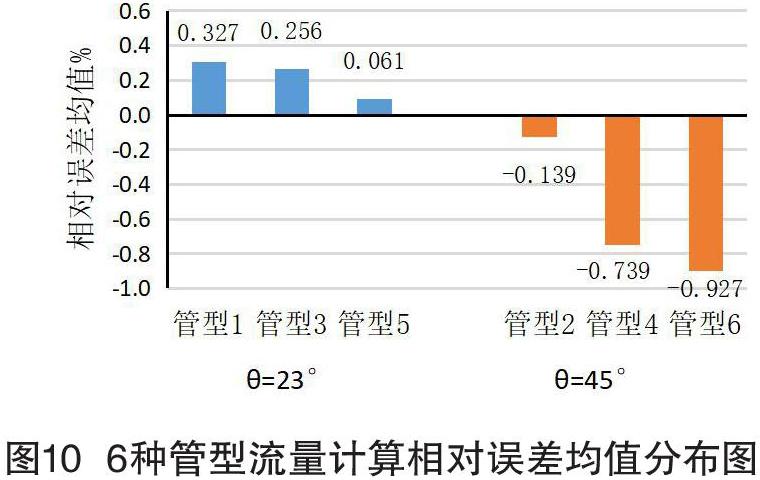
为研究文中推导的理论计算模型式（7）的计算精度，将前述实验得到的列于表1中的6种流量系数f1均值作为相应型号流量计实验件的理论模型式（7）的已知系数，对6个弯管实验件又进行了另外24次测流实验，将每组4次的测流流量实测值均值实测与理论模型流量计算值均值计算进行对比，并求取模型计算值计算相对于实测值实测的相对误差均值，各种实测与计算结果见表2所示。将6种实验管型的理论模型流量计算值相对误差均值按照两类方位角分组绘制成柱状图如图10所示。

对表2实验测试与模型计算数据及图10柱状分布图进行分析可得出如下结果：首先，理论模型流量计算相对误差大小与流量计实际所通过的流量关系密切，固定管型不同实验流量下的理论模型计算误差值均有所不同，无规律可循。但各实验管型的计算相对误差均值又表现出一定的规律性。即管型1、3、5的模型计算值表现出正误差，而管型2、4、6的模型计算值则表现出负误差。其次，由计算与实测结果的对比可知，流量计测压管的方位角大小对模型计算误差的正负特性有直接关联，23度方位角流量计会带来正误差，而45度方位角的流量计则会带来负误差。再者，模型计算流量相对误差绝对值的大小与流量计弯管的曲率半径r值大小有关，具体表现为23度方位角的流量计相对误差均值的绝对值随曲率半径r增大而减小，而45度方位角的流量计相对误差均值的绝对值随曲率半径r增大而增大，6种实验管型中，管型2与管型5对理论模型计算流量引起的平均相对误差最小。

4  结论

（1）利用方形弯管流量计及其理论计算模型式（7）可有效测算管中所通过的流量。各种管型流量计的流量模型计算平均误差范围约为-0.93%～+0.33%之间。

（2）理论模型计算流量引起的相对误差均值与所采用的弯管流量计的管型有关，即与测管方位角θ及弯管曲率半径r的取值有关，具体表现为较小方位角的流量计相对误差均值数随曲率半径r增大而减小，而较大方位角的流量计相对误差均值数则随曲率半径r增大而增大。

（3）使用较小方位角的测管管型1、3、5会引起正误差，而使用较大方位角的测管管型2、4、6则引起负误差。

（4）6种实验的方型弯管流量计中以管型2与管型5的综合测算误差相对较小，其中采用曲率与水力半径之比值r/R相对较大、方位角相对较小的管型5流量计为最优，引起的误差最小，约为+0.61‰。

（5）本文仅对6种管型流量计的测流参数性能进行了研讨，得出了有实际应用价值的结论，但对更多管型的测流参数性能还有待进一步研究。

参考文献

[1] 闫照辉.复杂工艺管道巧用弯管流量计实现流量测量[J].仪器仪表与分析监测，2016（4）：27-29.

[2] 裴晓迟，李耀刚，龙海洋，等.弯管流量计在测量上升管流量中的优势[J].华北理工大学学报：自然科学版，2018，40（2）：75-78.

[3] 琚立颖，王鑫阁，李耀刚，等.弯管流量计动态质量评价研究[J].现代制造工程，2016（11）：106-109，33.

[4] 吕鸣宇，李占贤.小直径取压孔弯道流量计的流量系统实验[J]，信息系统工程，2017（1）：119.

[5] 赵延军，黄晓飞.基于弯道流量计的煤粉质量流量监测[J].工业安全与环保，2018，44（8）：99-102.

[6] Jared C.Justensen， Stenven L.Barfuss，Machael.C.Johnson.  Effect of Meter Orientation Downstream of a Short Radius Elbow on Electromagnetic FlowMeters[J].J.Irrig. Drain Eng，2019，145（2）： 06018009-1-06018009-7.

[7] 纪波峰，纪纲.新型差压流量计的结构与性能研究[J].自动化仪表，2019，40（4）：77-81.

[8] LIU He-nian. Fluid Mechanics[M].China Construction Press， 3rd edition， January 2016：128-131.