初中数学变式训练教学切点探微
陶长海
(江苏省高邮市送桥镇初级中学 225600)
一、一题多解
所谓一题多解是指从多个方面、多个角度分析同一个问题,结合所学数学知识,根据问题提供的条件建立数学模型,运用多种解题方法解决同一个问题的思维方式.一题多解的本质是解题方法、解题思维的变式,无论何种水平的学生都可以参与,在积极参与中取长补短,查缺补漏.

例如,在右图所示的矩形ABCD中,对角线AC上有一点O,以OA为半径的圆O分别交AD,AC于点E,F,∠ACB=∠DCE,请问
(1)直线CE与圆O存在什么样的位置关系?请证明.
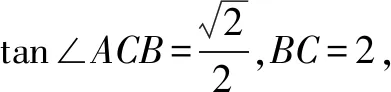
这个题目涉及到勾股定理、圆、矩形、三角函数等数学知识,需要运用作辅助线的数学思想方法,具有一定的综合性,思维跨度较大,可以有效考查学生综合运用数学知识的能力.为了更好地发挥该题目的教学作用,初中数学教师可以引导学生从多个角度去解答题目,开展一题多解变式训练.
解析(1)如上图所示,直线CE和圆O的位置关系是相切.ABCD为矩形,因此,AD与BC平行,∠DAC=∠ACB.又因为∠DCE=∠ACB,可知∠DAC、∠DCE相等.连结OE,可得∠DCE、∠AEO、∠DAC相等.因为∠DCE、∠DEC之和为90°,∠DCE、∠AEO之和为90°,可知∠OEC为90°,由此可证明直线CE和圆O为相切的位置关系.
问题(2)的解法有多个,教师可以引导学生尝试用多种解题方法解答这个问题.

解题方法2AE等于AD与DE的差,等于1.


通过一题多解变式训练,可以引导学生从多个角度去分析、解决问题,更加深入地理解和掌握问题涉及的知识,有助于提升学生的学习能力.
二、一法多用
在初中数学教学中,教师可以引导学生总结归纳题目立意、解题方法以及解题误区等,帮助学生构建更加完善的知识体系,同时可以考查学生对多个知识点的掌握,通过一题解答实现解一类题的教学效果.
原题目:已知关于x的方程3x-(2a-3)=5x+(3a+6)的解大于0,请问a的取值范围是多少?
变式题目1:

变式题目2:
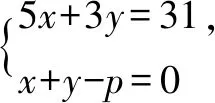
变式题目3:
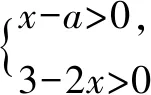
这组变式题目的共同点是都需要求解题目中出未知量以外的字母取值范围或具体数值,解题思路也大致相似,都是先解方程、方程组或不等式组,用所求字母表示解,然后将问题转换为不等式的问题,最终求得答案.
综上所述,变式教学方法的掌握是一个长期的过程,不可一蹴而就,这需要初中数学教师在平时的教学注意积累经验,收集教材中、教学辅助资料中的典型题目,将这些题目进行合理变式,在整理变式题目的过程中做到变式题组具有差异性、层次性、内涵性,才能确保变式训练教学达到预期效果.

