应用MS Excel求解三参数威布尔分布函数的参数估计

刘子娟， 郑学斌， 郭小军

（1.中国湖南航空动力机械研究所，湖南 株洲412002；2.长沙升华微电子材料有限公司，长沙410000）

0 引 言

在机械零件的疲劳试验数据统计分布中，广泛应用正态分布或对数正态分布[1]。但是，当机械零件失效概率很小时，用正态分布评估的疲劳寿命趋近于0[2]。威布尔分布是瑞典物理学家Waloddi Weibull在分析材料强度时，根据实际经验推导出来的分布形式[3]，与常用的正态分布或是对数正态分布相比，三参数威布尔分布往往能更准确地描述零件疲劳强度或疲劳寿命的概率分布，这是因为三参数威布尔分布中有个位置参数，其表征机械零件的最小寿命或最低疲劳强度，这更能反映机械零件疲劳特性的实际。因此，三参数威布尔分布拟合精度更高，在机械零件强度及疲劳寿命评价中得到了越来越广泛的应用[4-5]。

能用于三参数威布尔分布参数估计的方法大多计算复杂[6]，需要通过Matlab或其他计算机语言编程来计算，对于不掌握这些编程知识的人员来说应用难度很大。而MS Excel是大多数普通人员常用到的软件，本文运用Excel自带的强大数学运算、统计分析程序，对三参数威布尔分布进行参数估计，以一组数据为例来说明如何使用Excel中的数学运算函数、规划求解功能，以实现快速、高效地求解三参数威布尔分布的参数估计问题。

1 三参数威布尔分布的寿命分布函数

分布函数为

式中：N为零件寿命，N≥γ；m为形状参数，m＞0；η为尺度参数，η＞0；γ为位置参数，在机械零件寿命分析中，γ作为零件的最小寿命值，表示产品的使用寿命在达到γ值以前不会失效。因此对于实际零件产品来说，γ≥0（特别地当γ=0时，三参数威布尔分布函数退化成二参数威布尔分布函数）。

对式（1）两边取2次自然对数处理后得到

设零件寿命估计的可靠度为R，根据失效率F与可靠度R（即存活率）的关系

对式（5）作适当变换得

然后对式（6）两边取自然对数后整理得

式中，NR为三参数威布尔分布在可靠度下R的寿命估计。

2 位置参数γ的求解方法

先给一个初始值γ0（γ0≤Nmin，Nmin为试验得到的零件寿命数据组中最小寿命），利用最小二乘法，可求的m值、B值。

式（8）、式（9）中，n为样本容量。

式中：

当线性相关符合度r值的绝对值趋近1时，说明两个变量之间线性相关良好。为了使r值的绝对值越接近于1，需要优化γ0值。

3 经验分布的累计失效概率选取

根据经验，设有n个产品进行寿命试验数据，按其失效寿命值Ni（i=1、2、3……n）由小到大排序为N1＜N2＜N3＜……＜Nn，对应的累积失效概率（经验分布函数）为F（N1）＜F（N2）＜……＜F（Nn）。其中第i个失效产品的累积失效概率F（Ni）可用中位秩算法求得

或用平均秩算法：

4 运用MS Excel进行三参数威布尔分布的参数估计

MS Excel具有强大的统计和计算功能，其内含的“规划求解”功能更是求解最优化问题的便捷计算工具。因此，在MS Excel中编制好相应的计算公式后，可以很容易求解出三参数威布尔分布函数中位置参数γ、形状参数m和尺度参数η的最优值，并且可依据得到的3个参数值，求出指定某个可靠度R值下对应的零件寿命值。

现就以下面一个例子来说明，如何使用MS Excel表格来对机械零件进行三参数威布尔分布的参数求解和寿命估计。

设某零件经疲劳试验，测得其疲劳寿命循环次数分别为：29 613、35 862、42 267、46 500、51 233、54 600、60 970、66 820、71 608、75 088、79 604、82 200、87 368、92 570、100 790，共15个值（单位：次）。然后按图1的样式在MS Excel中设置表格。

1）在单元格A2～A16中由小到大升序方式输入上述试验测得的疲劳寿命循环次数值。

2）在单元格G18中指定一个初始值γ0，此处取29 000（注意，γ0≤Nmin）。

3）在单元格B2～B16中依次输入序号1～15。

5）在单元格D2～D16中，计算Ni-γ0值。在D2单元格中输入公式“=A2-$G$18”，同样用下拉填充方式填充D3～D16单元格，得到D3～D16单元格中的计算值。

6）在单元格E2～E16中，计算1-F（Ni）值。在E2单元格中输入公式“=1-C2”，用下拉填充方式填充E3～E16单元格，在对应单元格中得到计算值。

7）在单元格F2～F16中，计算Xi=ln（Ni-γ0）值。在F2单元格中输入公式“=ln（D2）”，用下拉填充方式填充F3～F16单元格，得到对应单元格的计算值。

这样，我们就完成了计算表格制作的第1步。

接着，根据所选取的初始值γ0值，对图1表格中的第F列（X值）和第G列（Y）进行线性规划拟合计算,然后求出线性拟合方程的斜率m值、截距B值和线性相关系数r值。

在此调用MS Excel自带的函数命令进行计算以上所述的m值、B值、r值。

在单元格G19中输入“=SLOPE（G2:G16,F2:F16）”，调用MS Excel中的求斜率函数命令，求式（3）所指的线性拟合方程中的斜率m值；在单元格G20中输入“=INTERCEPT（G2:G16,F2:F16）”，调用MS Excel中的求截距函数命令，求式（3）所指的线性拟合方程中的-B值（即得截距B值）；在单元格G21中输入“=CORREL（G2:G16,F2:F16）”，调用MS Excel中的求相关系数函数命令，用以反映［Xi,Yi］线性拟合的相关程度，即线性相关性符合度r值；在单元格G22中输入“=G19”，即为形状参数m值；在单元格G23中输入“=EXP（-G20/G22）”，即为尺度参数η值；在单元格G24中输入“=INT（G18）”，即取位置参数γ值为整数。设置好上述初始条件（已经对位置参数赋予初始值），并输入相关计算公式后，得到了一组初始数据，如图1所示。

图1 Excel计算表设计

最后，使用MS Excel 2003中的“规划求解”功能估计位置参数的最优值。先在MS Excel中加载“规划求解”宏。加载完成后，选择“工具→规划求解”功能，打开规划求解参数对话框，如图2所示。

先将图2中的“设置目标单元格”设为单元格“$G$21”，且目标值“等于最大值”，即要求该单元格所代表的相关系数r值为最大值；再将图2中的“可变单元格”选为单元格“$G$18”，即表示位置参数γ0可发生变化。接着设置约束条件，由于零件的疲劳寿命有0≤γ≤N1（N1即为收集的零件寿命值中的最小值），点击图2中“约束”条件偏右的“添加”按钮，添加约束条件：$G$18＜=$A$2 和$G$18＞=0。

为了保证精度，点击规划求解参数对话框右侧的“选项”按钮，弹出对话框，如图3所示，并按照图3所示进行参数调整，然后点击“确定”，返回到图2所示的对话框。点击图2中的“求解”按钮，MS Excel将自动规划求解计算出最终结果，求解结束后弹出的对话框如图4所示，点击图4中的“保存规划求解结果”后“确定”。

最终得到规划求解后的新结果见图5所示，此时显示相关参数r值的最大值是0.996 240 275；位置参数值γ =10 292、形状参数值m=2.535 947 749、尺度参 数 值 η =62 220.315 37。其他参数的新结果可参看图5所示。

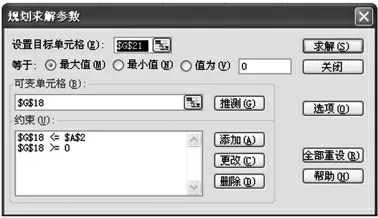
图2 规划求解参数对话框

图3 规划求解“选项”对话框

另外在单元格G25中输入指定可靠度R值，如输入0.9。在单元格G26中输入“=G24+G23*LN（1/G25）^（1/G22）”，即为式（7）所指的指定可靠度下的寿命值NR，此处NR=35 909，即经求出三参数威布尔分布函数的3个最优参数值后，零件的寿命服从该三参数值的威布尔分布，且当可靠度R值等于0.9的情况下，零件的疲劳寿命循环次数为35 909次。如图5所示。

图4 规划求解结果

图5 规划求解后的新数据结果

从上述运用MS Excel进行三参数威布尔分布的参数估计过程及形成的计算结果，可以看出，通过Excel制作相应的表格后，能快速、高效地求出威布尔分布的3个参数，并进一步评估出指定可靠度条件下零件的疲劳寿命值，而无需通过复杂的编程来求解。

5 结 语

1）本文根据线性相关系数最大化法则，利用MS Excel进行数据处理并求解三参数威布尔分布的3个参数，MS Excel表格制作简便，计算操作方便快捷，容易上手操作，可以在工程中得到推广和应用。

2）在使用MS Excel的“规划求解”进行参数估计时，要注意初始值的选择和求解精度的设置。初始值应尽量选择与最小失效寿命（N1值）接近，否则在进行规划求解后很可能会得不到满意的最优值。

3）由于累计失效概率有中位秩、平均秩等计算方式，采用不同的累积失效概率算法，三参数威布尔分布的参数估计和可靠性寿命估计的计算结果将稍有不同。