基于稀疏和低秩Hankel矩阵分解的SAR图像相干斑抑制①

蔡金萍 赵曜

(广东工业大学信息工程学院 广东广州 510006)

关键字：合成孔径雷达 相干斑抑制 低秩Hankel矩阵分解 稀疏

合成孔径雷达（Synthetic Aperture Radar,简称SAR）是用于地球环境监测、地质灾害调查等多种遥感应用的一项重要技术，具有全天时、全天候、工作距离远、高分辨率等优点，因而在遥感领域中得到了广泛的应用。与其他相干成像系统一样，SAR系统所成图像存在大量相干斑噪声，不仅影响了图像的质量，而且阻碍了图像信息的提取。因此，相干斑噪声的抑制是SAR图像处理中一个重要的步骤。

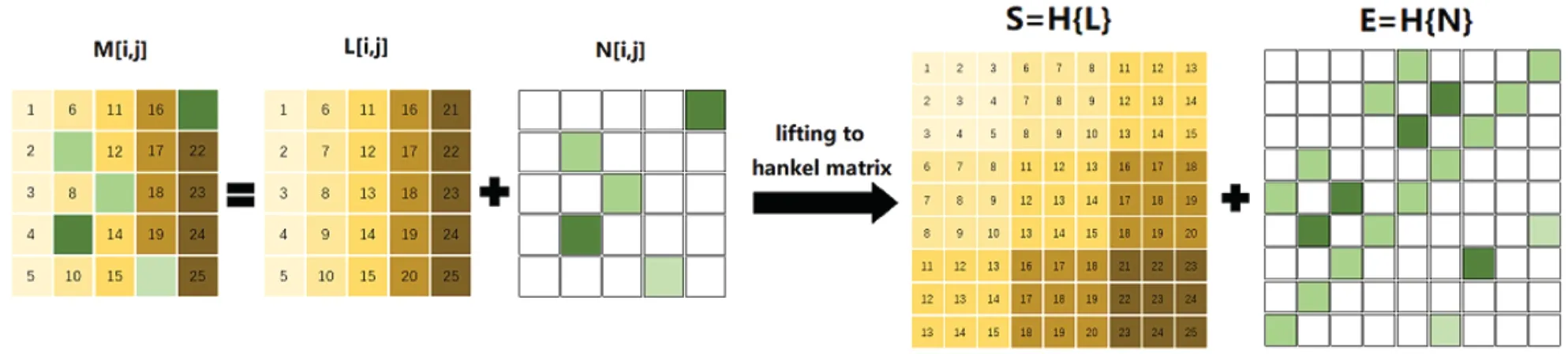
图1 含噪图像矩阵提升到Hankel矩阵的示意图

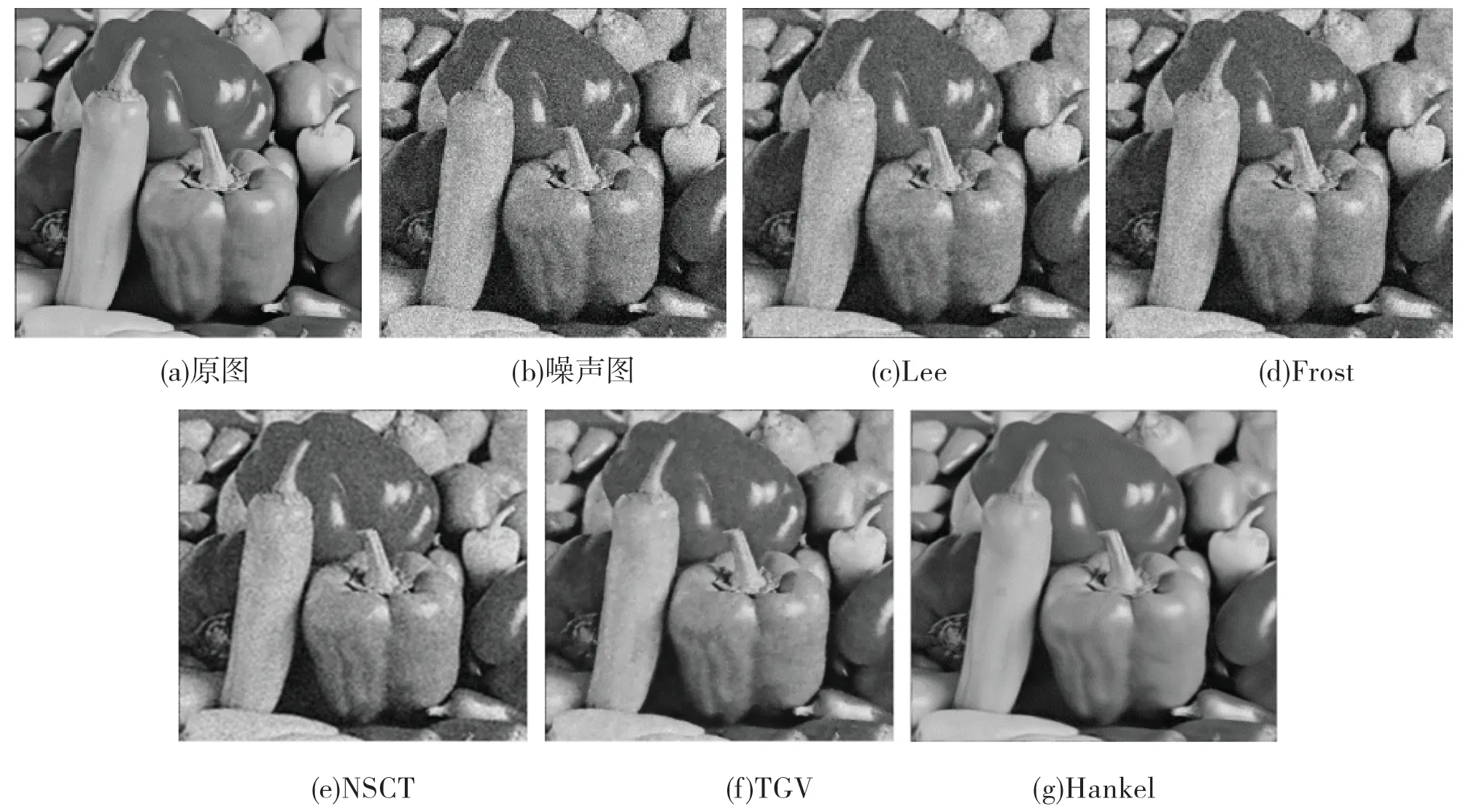
图2 图像Peppers降噪的效果图

目前，已经提出许多有效抑制相干斑噪声的方法，大体上可以分为成像前的多视处理方法和成像后的滤波器处理方法两个大方向[1]。其中Bhanu等[2]提出的多视处理方法通过降低处理器的带宽来形成多视子图，然后在各子图之间进行对应像素点的非相干叠加，从而有效地抑制相干斑噪声。此方法牺牲了空间分辨率，多视子图的增加会使得SAR图像的细节信息丢失。其中Lee滤波[3]、Kuan滤波[4]、Frost滤波[5]这几种滤波器方法的处理效率高、操作简单，但所得图像的清晰度和相干斑噪声的抑制效果和场景有关。随着变分和偏微分方程在图像处理中的应用不断深入，TV模型[6-8]和TGV模型[9]已经成功地应用到图像的去噪、修复以及放大等多个处理过程中，取得了可观的效果。文献[10]提出一种自适应总全变差方法，通过求解TV正则化式子来解决SAR图像相干斑噪声的问题，具有良好的图像锐度和边缘保持性能。针对TV模型阶梯效应的问题，Feng[11]等人提出一种基于总广义全变差的SAR图像相干斑抑制模型，该模型不能较好地恢复图像纹理。文献[12]提出了一种基于非下采样轮廓波变换（NSCT）和纹理模型的相干斑噪声抑制算法，利用纹理模型进行自适应阈值处理，从而得到边界清晰的图像，但该算法没有利用像素点及其领域像素的相关性，在去噪效果上容易出现局部亮点的现象。

图3 SAR河流区域图像的相干斑抑制比较图

图4 SAR山脉区域图像的相干斑抑制比较图

研究表明[13]，如果图像中存在噪声会导致频域中的频谱稀疏，存在一个与之相对应的湮灭滤波器，可以去除图像中的噪声。此外，可以根据湮灭滤波器构建低秩的Hankel矩阵，其秩由频谱域中的稀疏度决定。因而本文提出了一种基于稀疏和低秩Hankel矩阵分解的SAR图像相干斑抑制算法，利用Hankel矩阵自身所具有相关性，解决以上所述的不足。该算法主要分为两个阶段：第一个阶段，对SAR图像进行对数处理，然后提升到Hankel矩阵，接着利用鲁棒主成分分析进行低秩矩阵分解，从而解耦图像中的相干斑噪声分量。第二个阶段，利用交替方向乘子法（ADMM算法）解决该模型的优化问题。

本文将在第1节中介绍低秩Hankel矩阵分解的相关理论知识，其中1.1节介绍低秩Hankel矩阵的定义，1.2节介绍低秩Hankel矩阵分解模型。第2节将详细介绍所提算法的步骤。第3节将从模拟实验和真实数据的实验效果进行分析，验证本文所提算法的可行性和有效性。第4节将对全文工作进行总结。

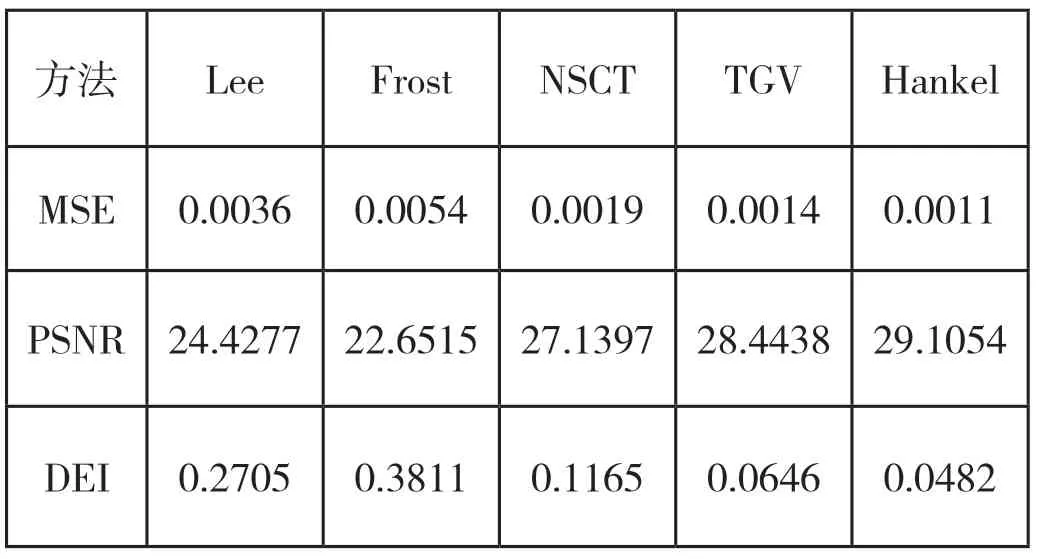
表1 图像Peppers降噪的评价指标比较

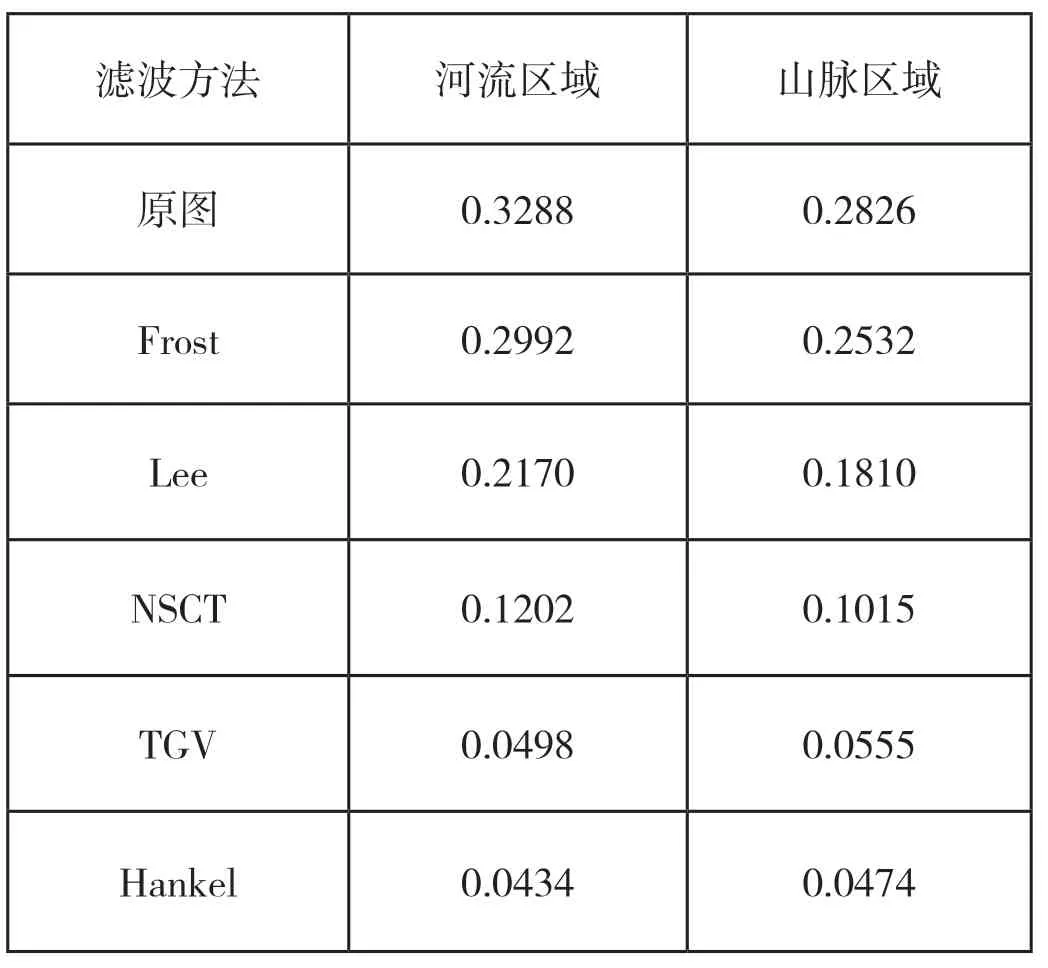
表2 不同区域相干斑抑制的评价指标比较

1 低秩Hankel矩阵的介绍及其分解模型

1.1 低秩Hankel矩阵

Hankel矩阵是一种特殊的结构矩阵，该矩阵在数值分析、图像处理、系统辨识等众多领域中具有广泛的应用。设离散数字序列为，则序列X的第i列向量一维Hankel矩阵可以表示为：

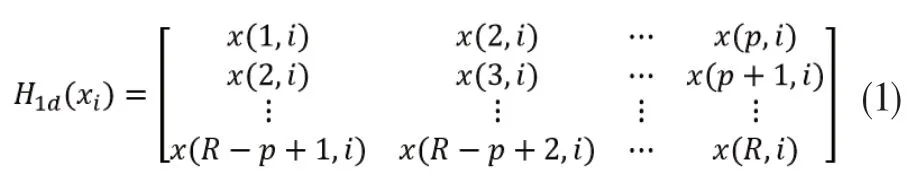
由式子（1）可以看出，矩阵的各行是由序列X以长度为p的滑动窗口截取得到，每次向右滑动1个距离单位，也就是说Hankel矩阵的反对角线上的元素是相同的，各行之间具有很大的相关性。

根据式（1）的一维Hankel矩阵，我们可以写出相应的二维Hankel矩阵，具体如下式子所示：

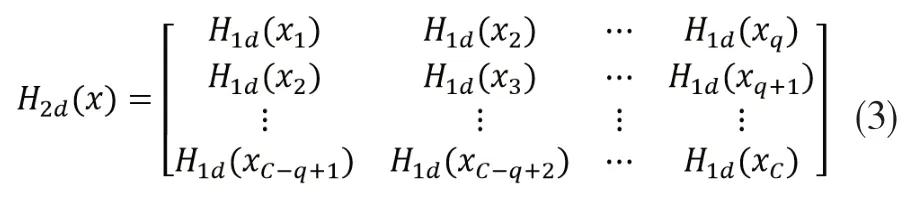
根据文献[14]的定理一可以得知，在含噪图像矩阵中，式（1）和式（2）是一个近似低秩矩阵，可以通过低秩Hankel矩阵分解的方法来进行图像降噪处理。

1.2 低秩Hankel矩阵分解模型

由上一节可知式（2）是一个二维近似低秩矩阵，利用文献[15]中所提鲁棒主成分分析（RPCA）方法进行低秩矩阵分解，可将该式子重写为：

其中H(x)表示对图像x提升到Hankel矩阵，S为低秩Hankel矩阵，E为稀疏Hankel矩阵。使用该模型进行噪声抑制是基于加性噪声的，而雷达相干斑噪声是乘性噪声，对SAR图像进行对数变换后，可以将乘性噪声转换为统计上独立于场景的加性成分。由于SAR图像信息大部分集中在低秩Hankel矩阵，而相干斑噪声主要由稀疏噪声引起的，所以在本文中设定S为提升到Hankel矩阵的相干斑噪声抑制SAR图像信号，E为提升到Hankel矩阵的图像噪声信号。

2 稀疏和低秩Hankel矩阵相干斑噪声抑制的算法

假设M表示含有相干斑噪声的SAR图像矩阵，L表示相干斑噪声抑制的SAR图像矩阵，N表示噪声组成的稀疏矩阵，则M可以表示为：

本文算法中根据Hankel矩阵所具有的线性性质，将L和N都提升到Hankel矩阵，如图1所示。

通过以上分析，假设N中的稀疏分量提升到Hankel矩阵中也是稀疏的，对于给定的SAR图像度量矩阵，为抑制图像中所含的相干斑噪声，可以模拟为解决以下最小化问题：

Hankel变换在本质上增加了矩阵的阶数，从而增加了求解计算的复杂度和内存需求。为了在一定程度上解决这一问题，对于式（6）的约束可以使用ADMM[16]方法处理，结合核范数分解[17]形式，可以写出其相应的拉格朗日函数：

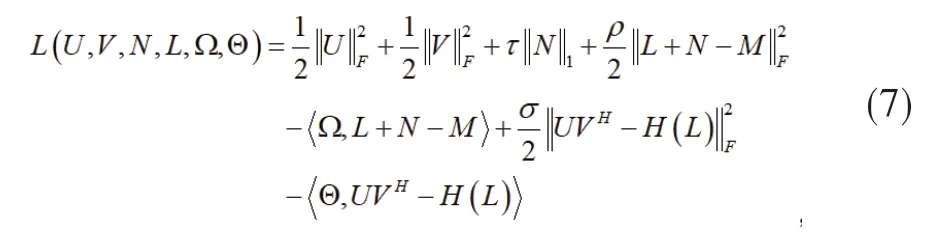
其中，U和V表示两个矩阵，上标H表示为矩阵的Hermitian转置，则H(L)可以表示为H(L)=UVH。Ω和Θ表示拉格朗日乘子，表示复数矩阵在希尔伯特空间的内积，ρ和σ为惩罚参数。则ADMM的迭代步骤为：

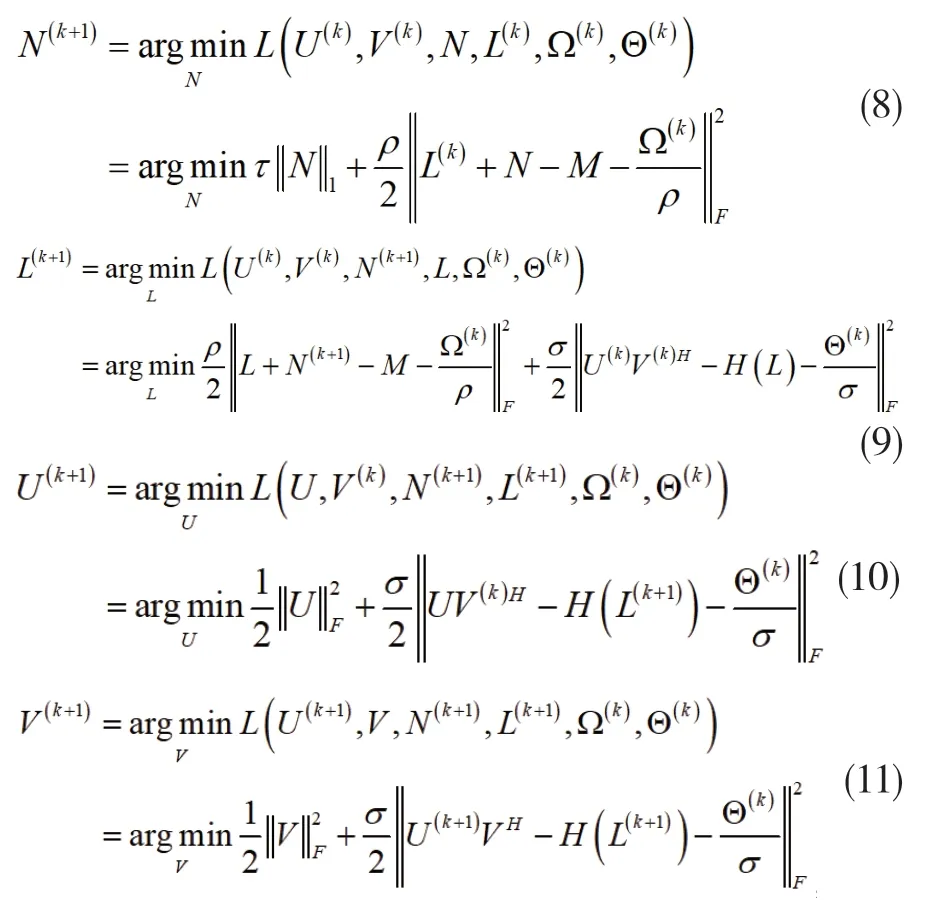
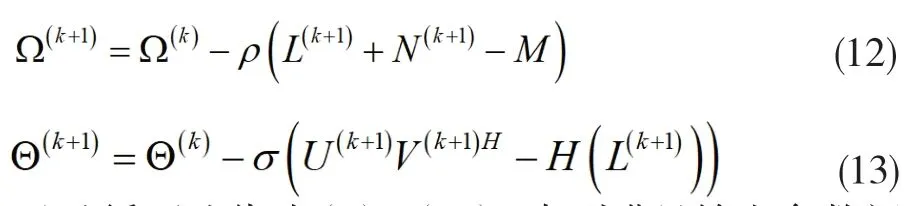
通过循环迭代式（8）-（13），直到满足输出参数阈值要求或者迭代次数要求，则输出优化求解结果，从而得到抑制相干斑噪声的SAR图像。

3 实验结果与分析

3.1 实验指标

本文将从两个方面评价本算法的性能与效果：第一，从主观效果进行人类视觉感官比较；第二，基于特定的参数进行定性分析。本文在模拟实验中引用了三个评价指标验证算法的有效性，分别为SAR图像相干斑噪声抑制性能指标（DEI）[10]、峰值信噪比（PSNR）和均方误差（MSE），DEI作为真实数据实验的主要参考指标。其中MSE指标表示真实值与预测值之间差平方的期望，反映两者之间的偏差，所以MSE的值越小越好。PSNR通常用来评价图像修复后与原图像相比质量的好坏，其值越大越好。而DEI是基于小邻域和大邻域标准差(std)比值设计的，用于评估SAR图像的边缘保持和相干斑噪声的去除效果，定义如下：

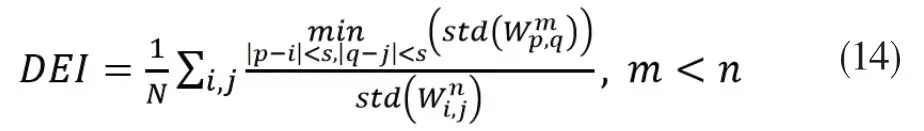
其中N表示SAR图像的总像素，表示以(p,q)为像素中心，图像大小为m×m的移动窗口，同理表示以(i,j)为像素中心，图像大小为n×n的移动窗口。在平滑的区域中，式（14）DEI的比值接近于1；而在边缘丰富的区域中，式（14）右侧的分母远远大于分子，DEI的比值远远小于1。也就是说，当分母窗口足够大，至少能覆盖一个真实的边缘特征时，DEI的值越小，SAR图像的相干斑噪声的抑制效果越好。

3.2 模拟图像斑点实验

实验使用了著名的光学图像Peppers，其中图像被添加均值为0，方差为0.02的高斯白噪声污染，然后将本文的算法和其他4种算法做比较：Lee[3]滤波、Frost[5]滤波、TGV[11]算法、NSCT[12]算法，实验结果如图2所示。

从图2可以看出，本文算法的相干斑噪声抑制效果最好，保持图像边缘信息的同时抑制相干斑噪声。表1给出了不同算法指标的比较，其中DEI指标使用5×5分子窗口和19×19分母窗口计算得到。根据表格可以得出，本文提及的算法都能够达到一定程度的相干斑噪声抑制效果，其中Lee滤波和Frost滤波的效果比较差，两者的MSE值比其他算法的大，PSNR值比其他算法的小。NSCT算法和TGV算法的效果比前两种方法好，而本文算法的MSE值和DEI值最小，PSNR值最大，相干斑噪声的抑制效果最好，说明本文算法的可行性。接下来将本文算法应用到SAR数据中，进一步验证算法在SAR图像相干斑抑制的有效性。

3.3 不同地区的主观效果图比较实验

3.3.1 基于SAR河流区域图像的实验

图3所示分别为SAR河流区域图像的Lee、Frost、NSCT、TGV和本文稀疏和低秩Hankel矩阵分解的实验结果，该区域有效的测试河面和陆地的相干斑噪声抑制能力，本文对这几种算法进行对比实验。从结果中可以看出，图3（c）Frost 滤波和图3（b）Lee 滤波处理的视觉效果最差，保持了完整的图像边缘，但仍然存在大量噪声；图3（d）NSCT算法视觉效果相对较好，存在零散的亮点，实验效果仍有待提高。图3（e）TGV算法得到了较好的抑制效果，存在细节信息有所丢失的问题。而图3（f）所示效果与图3（e）效果相近，但相比TGV算法，其边缘信息比较清晰和完整。

3.3.2 基于SAR山脉区域图像的实验

图4所示为山脉区域的实验结果。其中，图4（f）所示结果相对于其他几种算法，相干斑噪声的抑制效果明显，并且保留了原有山脉纹理和细节信息；Lee滤波处理和Frost滤波处理对图像进行了无区别平滑处理，处理效果不明显，相干斑噪声的问题依然严重。NSCT算法也有较好的视觉提升，但没有达到更好抑制相干斑噪声的效果。TGV算法的相干斑噪声抑制效果虽然较好，却丢失了山脉应有的细节和纹理信息。

3.4 特定参数的定性分析

为了进一步验证以上所提新算法的有效性，将从DEI指标进行定性分析。本实验针对上一实验选取的河流和山脉两个区域进行相关参数的计算，结果如表2所示。从表中可以看出5种算法都能够在一定程度上抑制相干斑噪声，不管是哪个区域，Frost滤波算法的DEI值最小，相干斑噪声的抑制最差；而Lee滤波算法相对于Frost滤波算法有一定的提高，但是效果不明显；NSCT算法和TGV算法的DEI值相对滤波器方法取得较低值，但图像的平滑性能和相干斑噪声抑制效果都有待提高；而本文所提算法DEI值最小，抑制效果最为明显，并且保存了图像的有效信息。对比不同区域之间的DEI可以发现，不管是在山脉等脉络清晰、具有明显高低起伏的区域，还是在河流等纹理简单、平缓的区域，本文算法的相干斑噪声抑制效果都最明显。总的来说，基于稀疏和Hankel矩阵低秩分解算法具有较好的性能，能够有效的抑制相干斑噪声，更有利于后续的应用处理。

4 结语

本文以SAR图像信号为研究对象，介绍了基于稀疏和低秩Hankel矩阵分解的SAR图像相干斑噪声抑制方法，将对数处理后的SAR图像信号进行Hankel矩阵提升，然后将Hankel矩阵分解的稀疏噪声信号做降噪处理，从而达到相干斑抑制效果。对比两种不同特征区域的实验结果可以看出，本文算法不管是河流区域还是山脉区域的图像，都能够更好地保留边缘细节信息和山脉纹理信息，提升图像的平滑性能，达到更好的相干斑抑制效果。