老年人长期护理服务质量评价指标权重构建

■ 石元伍 李婕

湖北工业大学工业设计学院 武汉 430068

0 引言

国家统计局最新公布数据显示，2019年我国60周岁及以上人口约为2.5 亿，占总人口的18.1%，其中65 周岁及以上人口约为1.8 亿，占总人口的12.6%，我国正加速进入深度老龄化社会。早在2013年9月，国务院发布《关于加快发展养老服务业的若干意见》中就提出了健全养老服务体系，满足多样化养老服务需求，2020年两会召开，全国人大代表郭红静同样也提出了要积极构建老龄健康服务体系和养老服务体系，可以看出，养老服务体系的建设一直是一个重要的问题，而系统且全面的养老服务评价体系则是养老服务体系建设中至关重要的一部分[1]。确定评价指标后，对指标权重进行科学量化，有助于体现各评价指标的重要度，保证评价结论的准确性以及养老服务改进方向的正确性。

在20 世纪60年代，国内外学者就对服务和服务质量（Service Quality,SERⅤQUAL）展开了研究。1982年，Gronroos 提出了“顾客感知服务质量”，认为服务质量是由顾客的期望与实际感知的服务之间的差距决定的，当顾客感知大于期望时，对服务质量满意度较高;当顾客期望小于感知时，则对服务质量满意度较低。1988年，由Parasuraman、Zeithaml、Berry[2]3 位学者组成的学术团队基于“顾客感知服务质量”这一概念，建立了SERⅤQUAL评价模型，从5 个维度对服务的质量进行评价。由于该模型适用性强，被学者们加以修正，广泛应用于养老服务质量评价中。 罗艳和石人炳[3]借鉴经典的SERⅤQUAL评价理论和方法，对虚拟养老院服务质量评价指标体系进行了初步探索。2019年刘晓辉[4]等人通过查阅文献、半结构式访谈、德尔菲法及层次分析法确立了针对护理院失能老年人的长期照护服务质量评价指标体系，具有较高的科学性,为护理院失能老年人长期照护质量的评价及服务指南的制定提供了参考。同年，杨帆[5]等人对SERⅤQUAL 模型进行修正，建立了老年长期护理服务质量评价指标体系，引入了层次分析法和德尔菲法对指标体系的权重进行界定。2020年刘超[6]等人运用德尔菲法和粗糙集法进行指标的筛选和权重计算，通过模糊隶属度方法确定各科室的评分结果，评估医院整体服务质量水平。杨燕清[7]等人以SERⅤQUAL 理论为指导,通过文献回顾、质性访谈、德尔菲专家咨询,拟定预调查量表，编制了失能老年人社区居家养老服务质量评价量表。郭飞[8]等人基于SERⅤQUAL 理论通过德尔菲专家咨询建立初步的评价指标体系,通过层次分析法来计算评价指标权重，建立医养结合养老机构服务质量评价指标体系。

从上述研究内容来看，养老服务质量评价体系的研究多是基于SERⅤQUAL 理论，采用层次分析法以及德尔菲专家咨询法进行评价指标权重界定的。我国养老服务体系建设还处在初级阶段，需要融入不同思维及方法从不同视角进行创新研究，层次分析法具有一定的局限性，在进行多层比较时，需要给出一致性比较，若不满足一致性指标要求，那么层次分析法就失去了作用，另外，在积极应对我国人口老龄化的问题中，国家越来越强调要以老年人为中心。基于此，文章尝试融入服务设计思想，提出一种基于序关系分析法的权重确定方案。服务设计作为一种社会变革的方式[9]，可以驱动社会创新，其设计思想要求必须从用户角度看问题，从用户出发，以用户为中心，满足用户的需求[10]。养老服务系统除了面向老龄用户外，主要还涉及到老龄用户的家属，尤其对于高龄失能老人来说，对养老服务进行评价的并不是老人本身，在进行权重界定时，老人与家属的意见均应得到参考。序关系分析法是在层次分析法的基础上进行改进的一种用来确定各阶段权重值的主观赋权方法，该方法不用构造判断矩阵也无需进行一致性检验，不易出错，计算过程较简便[11]。

本文引用修正后的顾客感知服务质量模型指标，对20名利益相关者进行问卷调查（包括老人和家属），采用序关系分析法确定评价指标权值，简化了评价指标体系的构建过程，为科学建立养老服务质量评价指标体系提供了新的思路。

1 服务质量评价指标体系的建立

将经专家讨论得出的老年长期护理服务质量评价指标体系的5 个维度和20 个指标进行可视化，如图1所示，M为我国老年长期护理服务质量评价指标体系，Mi（i＝1，2，...，5）为1级指标，Mij为2级指标（i＝1，2，...，5；j＝1，2，3，4）。

图1 老年人长期护理服务质量评价指标体系

2 服务质量评价指标权重的确定

2.1 基于序关系分析法的模型权重计算方法

设M1,M2,…,Mm(m≥2)是经过类型一致化和无量纲化处理的m 个指标，指标Mi的重要程度优于Mj时，记Mi＞Mj

第n 位利益相关者，确定序关系为M1＞M2＞M3＞...＞Mm

相应指标对应的权重系数关系为w1＞w2＞w3＞...＞wm

使相邻指标的间距保持一致, 用Mi*表示{Mi}按序关系“＞”排定顺序后的第k 个评价指标(k=1,2,…,m),则：M1*＞M2*＞M3*＞M4*＞M5*

相应指标对应的权重系数关系为w1*＞w2*＞w3*＞w4*＞w5*

最佳指标与用户评定指标对应关系如表1所示。

表1 最佳指标与用户评定指标对应关系

判断相对重要程度的比值，设定用户关于相邻评价指标Mk-1*与Mk*的重要程度权重wk-1*与wk*之比为：

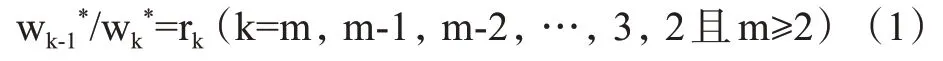
式中：wk*——第k个序号的权重

rk——权重距离

权重wk-1*与wk*的比值rk赋值关系如表2所示。

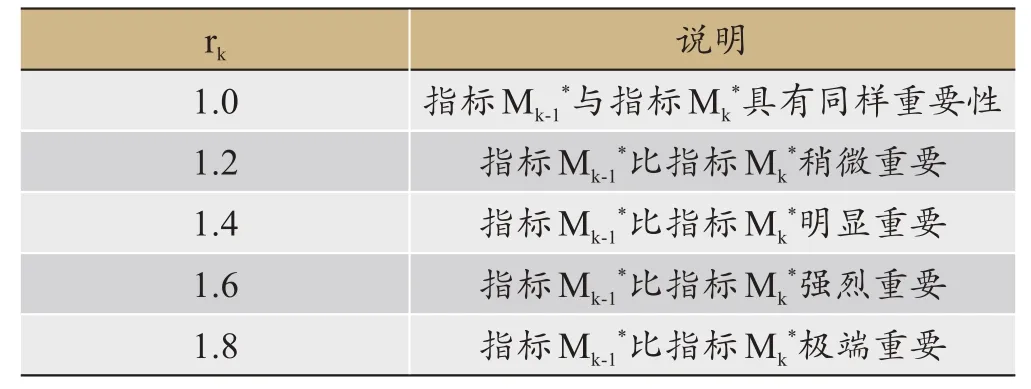
表2 rk赋值参考表

给出rk的理性赋值

由式（1）式（2）可得wm*,wm-1*,wm-2*,...,w1*

各评价指标权重系数为w1=w1*,w2=w2*,w3=w3*,...,wm=wm*

分别求出n 名利益相关者数据，求均值得到重要指标权值

2.2 基于序关系分析法的模型权重确定

采集样本20人，让每位利益相关者针对评价指标体系里的1 级指标和2级指标进行排序，根据指标的重要性，得到排序的结果，结果如表3所示。

表3 利益相关者指标排序结果

以第1 位利益相关者为例，确定1 级指标序关系为M2＞M4＞M3＞M1＞M5

相应指标对应的权重系数关系为w2＞w4＞w3＞w1＞w5

使相邻指标的间距保持一致,用Mi*表示{Mi}按序关系“＞”排定顺序后的第k 个评价指标(k=1,2,…,m),则：M1*＞M2*＞M3*＞M4*＞M5*

相应指标对应的权重系数关系为w1*＞w2*＞w3*＞w4*＞w5*

最佳指标与用户实际评定指标对应关系如表4所示。

给出rk的理性赋值为1.2

由式（1）式（2）可得w5*=0.134,w4*=0.161,w3*=0.194,w2*=0.232,w1*=0.279

各评价指标权重系数为w1=w4*=0.161,w2=w1*=0.279,w3=w3*=0.194,w4=w2*=0.232,w5=w5*=0.134

同理得到剩余19位利益相关者数据，求均值得到重要指标权值：

w1=0.18485,w2=0.24695,w3=0.19775,w4=0.22505,w5=0.1454

用同样的方式得到2 级指标排序。第1 位利益相关者，确定2级指标序关系为M14＞M12＞M11＞M13

相应指标对应的权重系数关系为w14＞w12＞w11＞w13

使相邻指标的间距保持一致,用Mij*表示{Mij}按序关系“＞”排定顺序后的第k 个评价指标(k=1,2,…,m),则：M11*＞M12*＞M13*＞M14*

相应指标对应的权重系数关系为w11*＞w12*＞w13*＞w14*

最佳指标与用户实际评定指标对应关系如表5所示。

表4 最佳指标与用户实际评定指标对应关系

表5 最佳指标与用户实际评定指标对应关系

2 级指标个数为4 个，为拉开指标之间的差距，给出rk的赋值为1.5。

由式（1）式（2）可得w14*=0.123,w13*=0.185,w12*=0.277,w11*=0.415

各评价指标权重系数为w11=w13*=0.185,w12=w12*=0.277,w13=w14*=0.123,w14=w11*=0.415

同理得到剩余19位利益相关者数据，求均值得到重要指标权值：

w11=0.2117,w12=0.3329,w13=0.1708,w14=0.2846

同理得到剩余指标权值：

w21=0.3091,w22=0.1915,w23=0.2862,w24=0.2132

w31=0.2108,w32=0.2838,w33=0.2600,w34=0.2454

w41=0.2961,w42=0.2816,w43=0.1692,w44=0.2531

w51=0.2254,w52=0.1932,w53=0.3268,w54=0.2546

通过序关系法得到1 级指标和2 级指标权重，如表6所示。

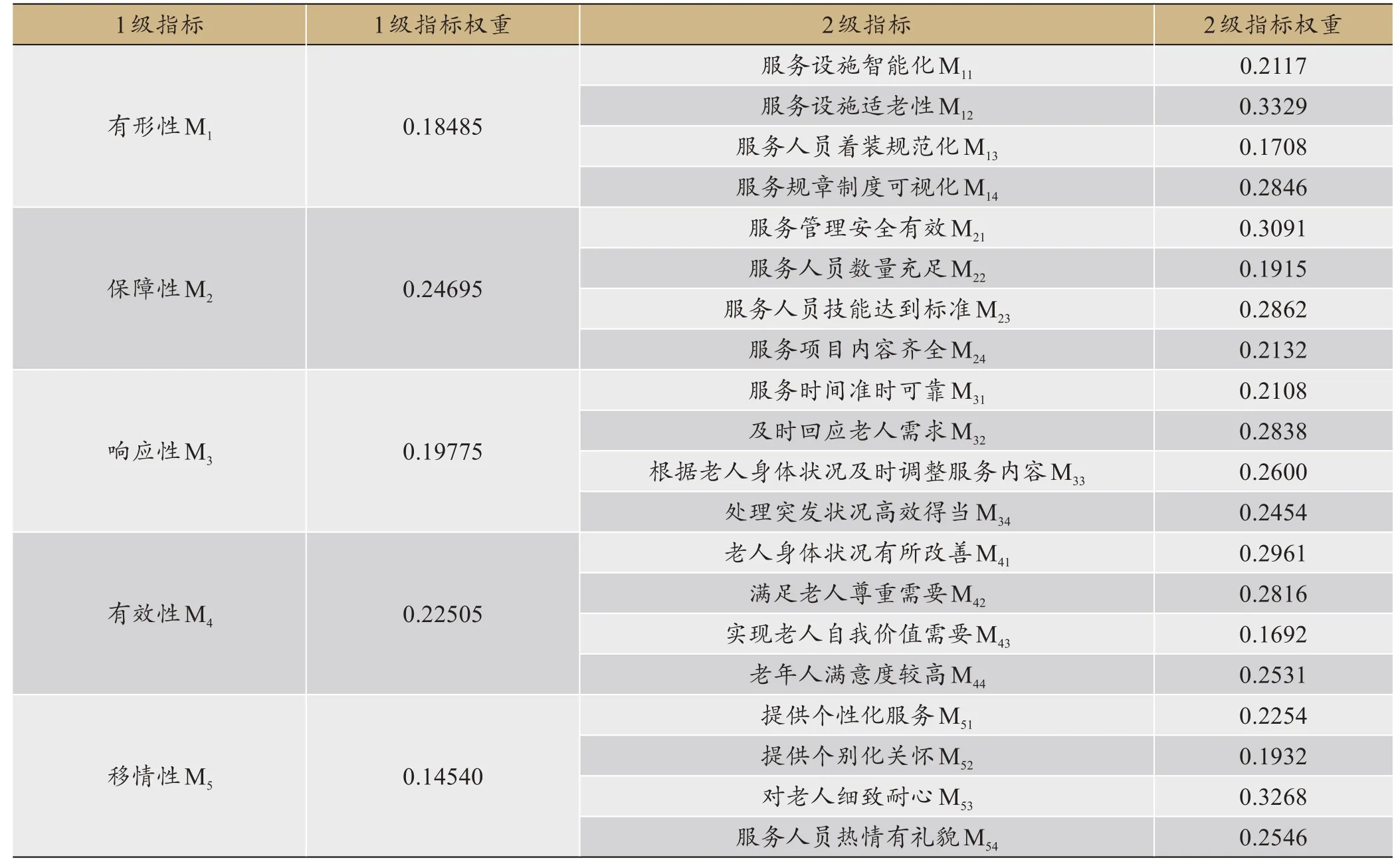
表6 通过序关系法得到的2级指标权重

对从属于1 级指标的2 级指标进行规范化，得到针对整体服务系统的权重，以便对全部2级指标进行比较。

式中：wij’——规范后的2级指标权重

wij——原2级指标权重

wi——各1级指标的权重

根据式（4）得到规范化后的2 级指标权重，如表7所示。

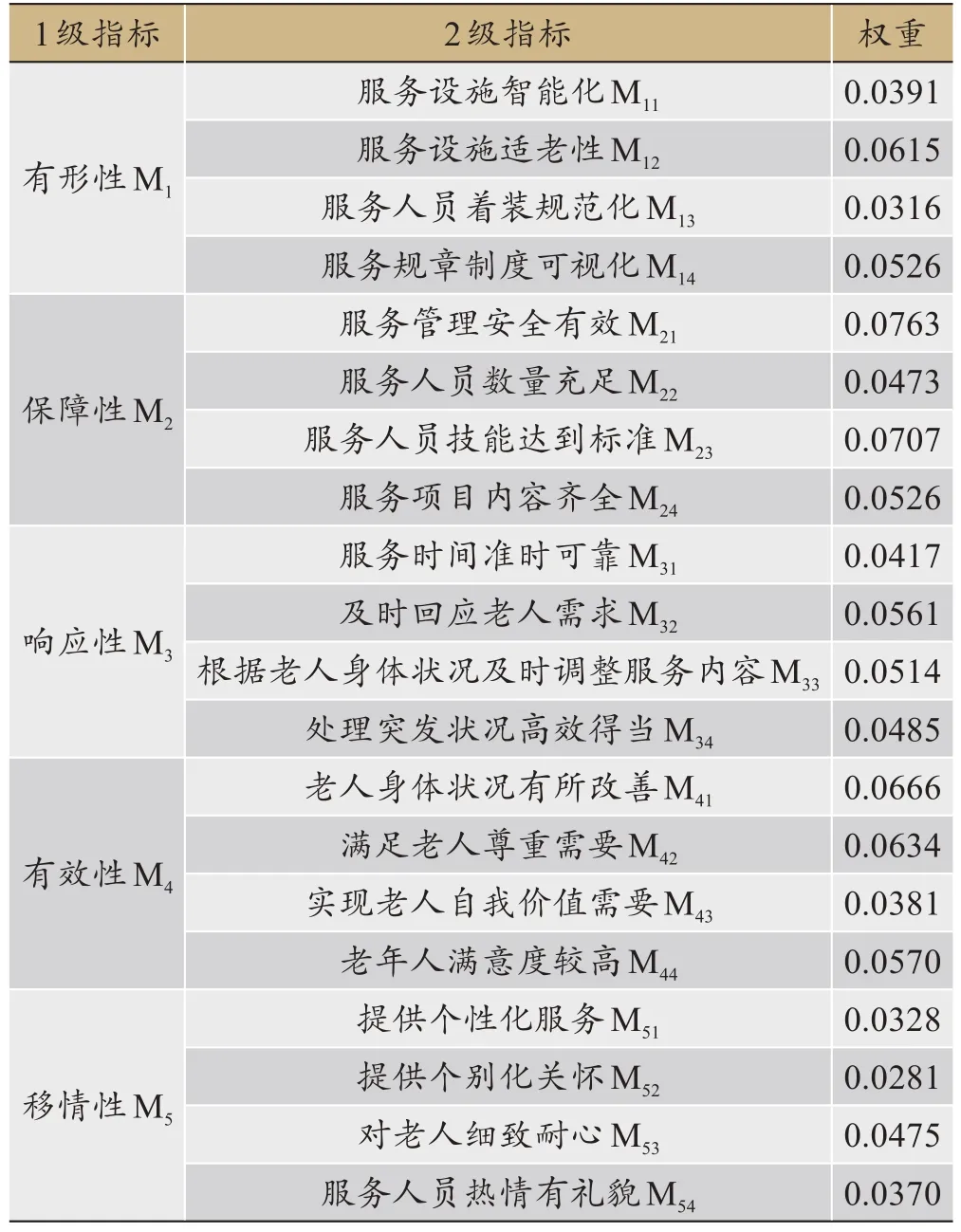
表7 规范化的2级指标权重

3 结果分析

由表7可得20 个指标重要度排序为M21＞M23＞M41＞M42＞M12＞M44＞M32＞M24＞M14＞M33＞M34＞M53＞M22＞M31＞M11＞M43＞M54＞M51＞M13＞M52

而杨帆[5]等人基于层次分析法，对20 位专家的打分进行权重计算，获得的指标重要度排序为M41＞M12＞M33＞M24＞M42＞M32＞M22＞M44＞M52＞M21＞M31＞M43＞M53＞M23＞M54＞M34＞M11＞M13＞M51＞M14

两种方式得到的排序结果差异较大，如M14，由专家评价得到的权重处于最后，但由利益相关者评价得到的权重处于第9。为了进一步证明结果存在差异性，进行两种赋权方式下所获权重值结果的对比分析，为便于观察，整体将权重值扩大100 倍，不影响对比结果，具体结果如图2所示。

由图2可知，两种方式得到的权值结果差异较大

图2 两种赋权方式所获权重值结果对比分析图

在某些属性特征上，基于序关系分析法利益相关者评价所获得的权值普遍较高于基于层次分析法专家打分所获得的权值；只有少数权值较为吻合，如M31、M43、M44；个别权值差别巨大，如M41。

以上结果存在差异性的可能性原因主要有3点：（1）采用的赋权方法不同。层次分析法存在主观判断性失误，影响结果，建议选择更加客观的权重分析方法：无需一致性检验的序关系分析法计算权重系数，使最终权重结果更准确、可靠性更高[12]；（2）访问的人群不同。主体人（调查对象）对客体物（调查目标、内容）在不同层次或角度上的认知差异水平，稍有偏差就会导致结果出现不可靠性、误导性等问题[13]，当权重评价人群为利益相关者，而非专家时，权重会发生改变，是否应该一改往常专家打分的习惯，变为由老人本身及利益相关者评价；（3）调查的时间不同。研究调查时间相隔大约有半年以上，随着生活水平的提高，人民幸福感加强，在不同阶段,市场和用户需求发生变化，对长期护理服务质量评价指标的重要度排序也会发生变化，长期护理服务质量评价指标的权重也应该及时的修正和优化。

4 结论

老龄化问题是一个非常复杂的问题，跨学科研究是必然趋势，文章基于养老服务质量评价体系背景研究，融入服务设计理念，采用序关系分析法进行权重构建，可以得到以下结论。

（1）我国正加速进入深度老龄化社会，养老服务评价体系研究尚处于初级阶段，采用非直线的、能够推动社会创新的设计思维来看待人口老龄化的研究并不多，应当加强跨学科研究，保证养老服务体系建设的科学性合理性。

（2）在服务质量评价指标权重构建中融入服务设计思想，以用户为核心。相较于通过专家打分的方式获取权重值，采用利益相关者评价的方式更能强调用户主观能动性，更加符合实际，结果更有针对性和说服力。

（3）运用序关系分析法，对专家研究得出的老年长期护理服务质量评价指标进行权重计算，使得过程更加简便，最终结果更为准确、可靠性更高。

（4）赋权方法的不同、访问人群的不同以及调查时间的不同均可导致结果具有差异性，后续研究可针对3种导致结果差异性的可能性原因进行分析，设置单一变量，找到影响权重赋值结果的因素，从而使养老服务评价体系的构建更为可靠、合理。