自由式滑雪空中技巧跳台场地尺寸变化对运动员出台速度影响的研究

刘忠源，李 东，付彦铭，王 新*

自由式滑雪空中技巧是我国备战2022 年北京冬奥会中的重点项目之一，更是冲击金牌的重要项目之一。该项目整套动作由助滑、起跳、翻腾转体和落地4 个阶段组合而成。但由于比赛在户外场地进行，影响运动成绩的因素比较复杂多变。研究表明，影响动作成功率的重要影响因素之一在于出台速度，合理的出台速度是整套动作的基础，相宜的出台速度可以为运动员在完成动作时获取更为适宜的落地体位角度，使其落地趋于平稳。适合的出台速度是完成动作的前提（王新等，2011；闫红光等，2010）。出台速度是由场地尺寸、运动员滑行距离、滑行姿势、滑行速度、雪的摩擦系数和空气阻力等因素共同决定，场地因素是影响运动员出台速度的主要因素，其中跳台场地各位置尺寸的变化会对运动员的滑行速度造成影响，从而影响出台速度（马毅等，2010；佟永典 等，2003；王新 等，2011；徐囡囡 等，2017；闫红光 等，2010）。

有研究表明，随着助滑坡的坡度增大、垂直高度增高，助滑速度增快；过渡区越长、跳台高度越高，会造成出台速度变慢。助滑坡的垂直高度增高，相对势能越大，转化动能就越大，助滑速度也越快。由于过渡区是一段水平的区域，随着过渡区的加长，摩擦力做功变大，导致原有助滑速度降低。跳台区的曲线弧度越大，向心力增大，切向下滑的分力减小，导致助滑速度降低，进而影响出台速度。

近年，数值仿真计算以其强大的计算精度和高效的仿真效果等优势，在体育动作分析中广泛应用。国内外学者对不同体育项目动作完成质量进行仿真分析，最为常见的是转体类项目的情况分析（Mössner et al.，2011）。滑雪技术的模拟计算主要以高山滑雪为主（周娟等，2015），通过研究不同的滑雪板，分析其在雪地上的压力分布情况（Glenne et al.，1997）。还有针对个别滑雪技术的研究，通过实验测量方法测试不同坡度（Millet et al.，1998）、雪杖的不同长度（Nilsson et al.，2003）、不同动作频率（Hoffman et al.，1995；Holmberg et al.，2006）对撑雪技术的影响。Holmberg 等（2005）研究了撑雪技术对下肢动作的影响，并用AnyBody 软件建立了力学模型，仿真研究上肢在撑雪技术中的作用。但由于空中技巧的复杂性，鲜见对于空中技巧项目的仿真计算。由于比赛和训练场地的不同，跳台尺寸会略有差异，而且完成不同动作也需要从不同尺寸跳台腾起获得不同的出台速度和高度。相关研究围绕该项目的制胜特征展开系统分析，深刻了解其特性、训练规律，并在此过程中发现训练中存在的不足，并提出改进的建议。基于此，本研究利用数值计算方法模拟计算跳台场地尺寸变化对运动员出台速度的影响指标总结不同场地尺寸对出台速度的影响结果。

1 研究对象与方法

1.1 研究对象

以我国自由式滑雪空中技巧国家队优秀运动员为研究对象，男、女各5 人。其中，男运动员平均身高（1.74±0.02）m，平均体质量（71.60±4.93）kg；女运动员平均身高（1.63±0.04）m，平均体质量（53.60±4.87）kg（表1）。根据运动员身高、体质量信息情况和完成动作特点，为简化计算模型，三周台人体三维建模对象为2018 年平昌冬奥会男子自由式滑雪空中技巧亚军贾XX，两周台人体三维建模对象为获得4 次世界杯总冠军的女子自由式滑雪运动员徐XX。采用北京体育大学三维人体扫描仪（An‐throscan 3D VITUS）建立6 个特定姿态的三维模型计算空气阻力。数值模拟验证对象为运动员在训练期间所做动作的出台速度解析结果。视频按照男、女完成不同跳台的不同难度系数的动作进行整合。

1.2 研究方法

1.2.1 数学计算法

选用数学计算软件Matlab 对运动员在跳台场地尺寸（表2）变化时运动员的出台速度情况进行仿真，并将理论与实验结合，进行数学建模分析，建立助滑阶段的运动方程、跳台运动方程和出台运算方程，计算出台速度。

1.2.2 影像解析法

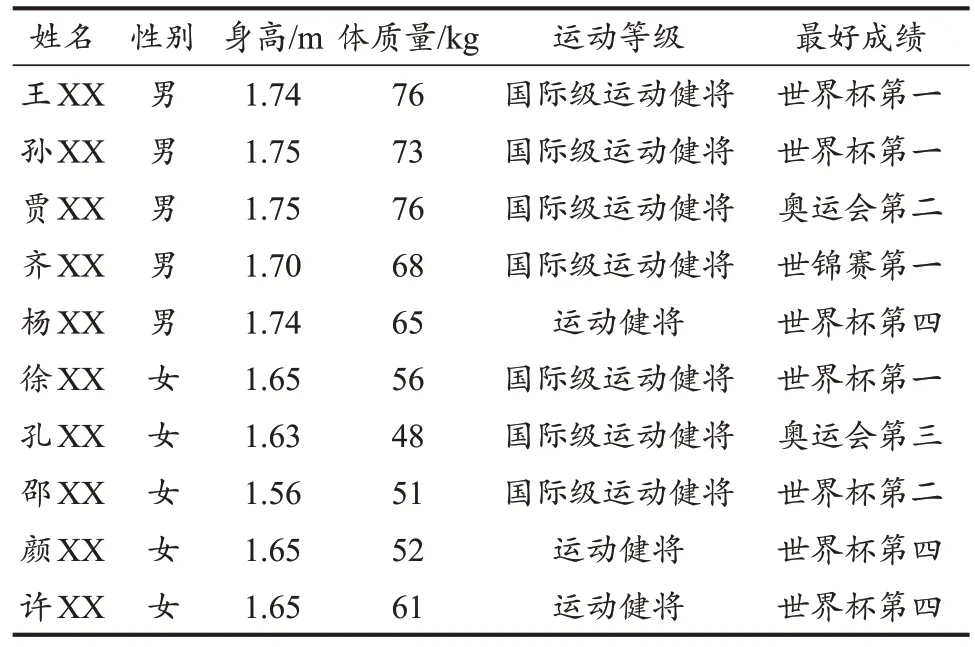
表1 研究对象基本情况Table 1 Basic Information of the Research Objects

表2 跳台场地尺寸Table 2 Site Size

实验验证采用平面定点测量的方法，使用3 台采样频率为50 Hz 的SONY 高清耐低温摄像机，分别对起跳和落地的正面、侧面进行定点同步拍摄。1 号摄像机架设在距离跳台场地约11 m、高3.8 m 处，主要对上台起跳阶段动作的水平位置进行拍摄，获取出台动作和空翻最高点；2 号摄像机架设在距离比赛场地约11 m、高1.6 m 处，主要对落地阶段动作的水平位置进行拍摄，获取运动员落地动作；3 号摄像机架设在距离比赛场地约11 m、高7.6 m处，对整套动作进行全程拍摄（图1，图2），获取运动员完整的动作，由此判别运动员动作完成的质量。在采集之前，对场景进行标定，拍摄框架为爱捷001-A 型三维DLT立体辐射框架，为了更加方便地寻找关节点，运动员需穿着深色服装，并将关节处贴上标志点。采用美国艾利尔运动生物力学分析系统（Ariel Performanace Analysis Sys‐tem，APAS）对所采集的运动录像进行人体各关节点的数字化处理，系统标定精度0.001 m。以松井秀治模型参数为标准，手动逐帧标定人体21 个点位，经过数字化计算得到整个助滑过程中重心点位置、位移、时间、速度等运动学参数，采用低通数字滤波法平滑原始数据，截断频率为6。

1.2.3 统计分析法

使用SPSS 21.0 进行数据处理，结果采用平均值±标准差的形式展示，数据通过对仿真计算与实际测量的差异进行检验，所有测试的概率水平设置为0.05，具有显著性差异。同时，运用皮尔逊相关系数，验证仿真计算与实际测量结果的相关性，0＜r＜0.4 弱相关，0.4≤r＜0.7 中等相关，0.7≤r≤1 强相关。

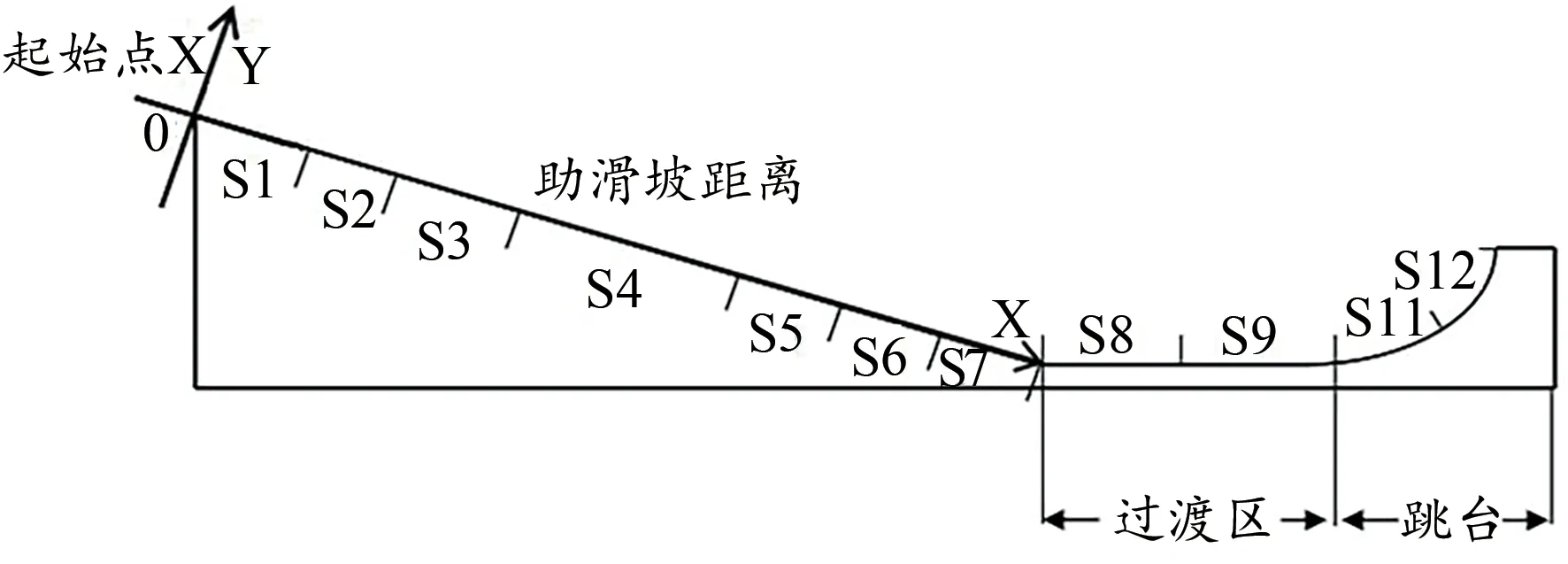
图1 助滑区域划分图Figure 1.Division of Sliding Zone

2 结果与分析

采用实际拍摄解析的出台速度验证模拟结果，因此，数学模型中变量定义为在实际拍摄时场地环境的实时数据（表3）。通过改变各项相关尺寸进行方程运算。

2.1 运动方程的建立

2.1.1 助滑坡上运动方程的建立

考虑到其他影响因素，如空气阻力、运动员从不同位置出发的速度是不同的，特选择力是坐标的函数来求解运动方程，即运动员在助滑坡上所受各力均表示为力随助滑坡位置变化的函数，根据牛顿第二定律的积分表达式：

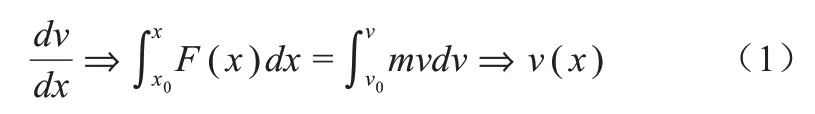
其中，x为滑行距离，助滑开始时x=0，v为运动员滑行速度，α为雪道倾斜角，G为重力，N为支持力，f'为空气阻力，f为摩擦力，L为升力（图3）。运动员在滑行过程的不同阶段进行动作调控，即阶段不同时身体姿态也发生相应变化，对雪面产生一个作用力，同时雪面也给人体一个支反力N，N可以分解为平行于雪面的力Nx、垂直于雪面的力Ny、沿身体横轴的力Nz（其对助滑速度方向影响很小，所以忽略）。

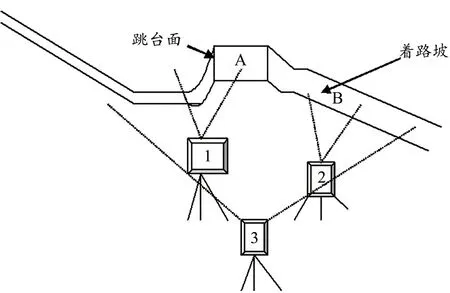
图2 拍摄地3台摄像机架设位置Figure 2.Location of Three Cameras in the Shooting Site

表3 数学模型中变量数值Table 3 Values of Variables in the Mathematical Model

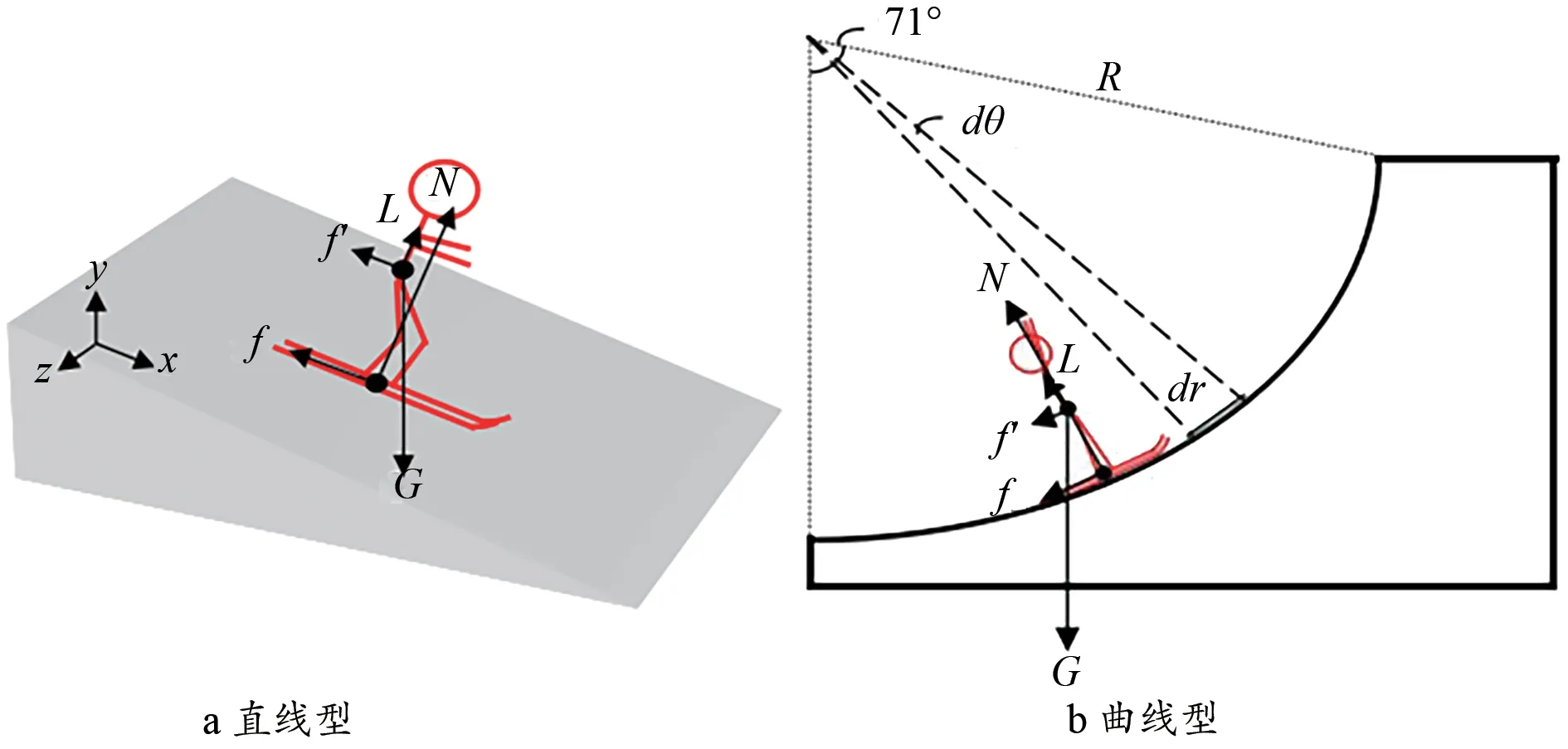
图3 运动员受力图Figure 3.Diagram of Athlete

根据公式（1），助滑坡上运动员沿坡面方向的运动方程如下：

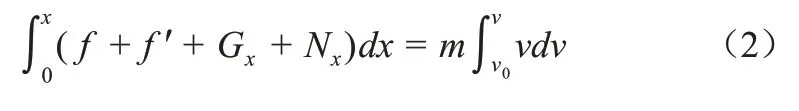
2.1.2 跳台阶段运动方程的建立

运动员在滑入跳台弧度区域之前，身体已经保持直立举臂状态，并处于该固定姿势上台。由于运动员动作未发生改变，同时为了简化计算，此过程忽略人体支反力变化对出台速度的影响。考虑在此阶段运动员始终在曲面上滑行，将曲率半径视为定值，出台速度方程采用动能定理进行计算（图3），方程如下：

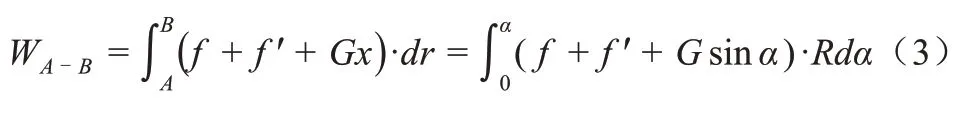
升力和支持力与位移方向垂直，所以不做功。

2.2 出台速度控制方程的运算

采用欧拉算法，对两段的常微分方程进行求解。假设式y'=f(x，y)(a≤x≤b)中的f(x，y)充分光滑，将y(xi+1)在xi点作Taylor 展开：

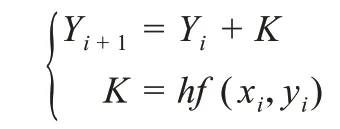
根据公式（1）有dv=，当∆x很小时，有dv≈∆v=K·∆x，所 以dv=f'(xi)∆x，f'(xi)=。根 据Taylor 展开公式速度的方程为：

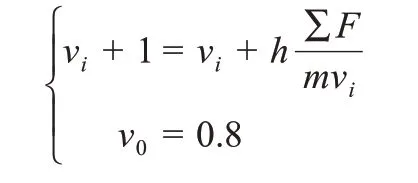
通过特定环境条件的定义，改变方程中的变量（场地尺寸）进行运算。

2.2.1 助滑距离改变对出台速度的影响

研究证明，助滑距离越大，助滑速度越快；助滑距离越小，助滑速度越慢，间接影响运动员重心出台合速度（马毅等，2016）。根据抛体运动特点，运动员出台时重心垂直速度又直接影响运动员起跳腾空高度，出台时重心垂直速度越大，运动员的腾空高度越高，滞空时间也相对越长，运动员即可完成难度更高的多周转体动作。对不同助滑距离时的速度进行对比分析，助滑过程的最大速度都出现在助滑坡最接近过渡区的滑行区域，进入过渡区速度开始逐渐呈现递减趋势，在出台时速度最小（图4，表4）。当助滑距离增加了10 m 时，会使出台速度增加1.1 m/s。

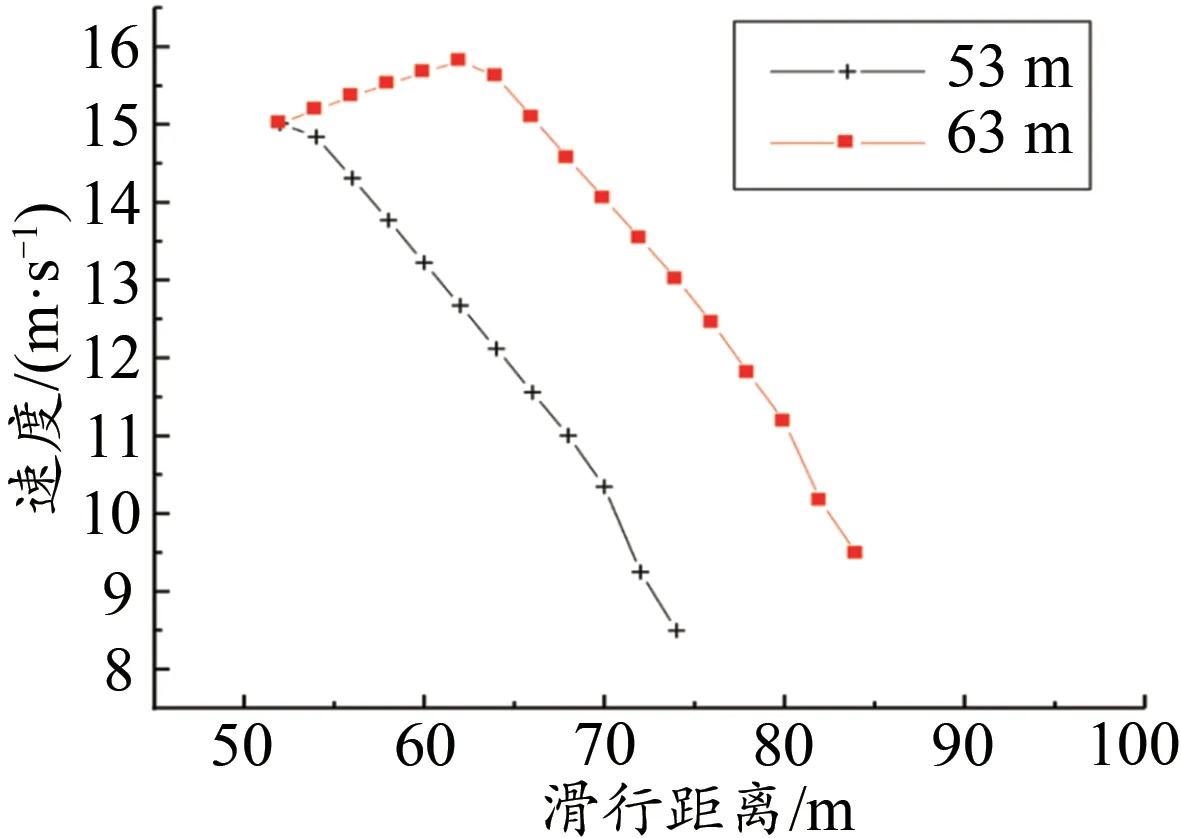
图4 运动员在不同助滑距离时速度变化Figure 4.Speed Changes of Athletes at Different Distances

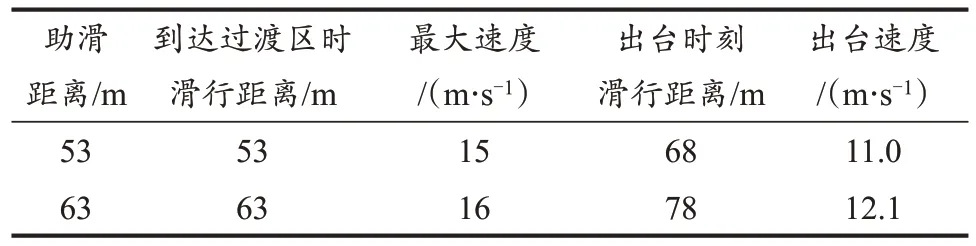
表4 助滑距离的改变对出台速度的影响Table 4 Influence of the Change of Sliding Distance on the Takeoff Speed

2.2.2 过渡区距离对出台速度的影响

过渡区是相对较为水平的滑行区域，在该区域运动员主要完成对速度的感知把控和上台前的身体姿态调整工作。但是由于此滑行区域没有坡度，重力不产生重力加速度，空气阻力与摩擦力起主要作用，所以过渡区的长短会直接影响上台速度的大小，进而影响到出台速度。研究表明（图5，表5），过渡区为10 m 时，出台速度为11 m/s；当过渡区距离增长至约15 m 时，出台速度为9 m/s；过渡区增长至约20 m 时，出台速度递减到6 m/s。由此可知，过渡区的长度变化对出台速度影响较大，出台速度同过渡区长度呈负相关关系。

图5 过渡区长度对出台的速度影响Figure 5.Influence of the Length of Transition Zone on the Take-off Speed

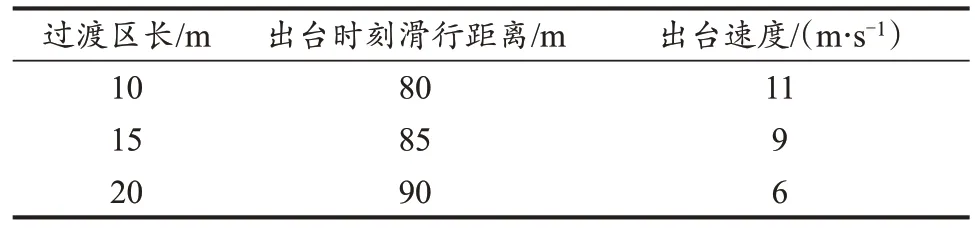
表5 过渡区的延长对出台速度的影响Table 5 Influence of the Extension of Transition Zone on the Take-off Speed

2.2.3 跳台尺寸变化对出台速度的影响

当场地助滑距离和过渡区长度相同时，同一运动员从两周台起跳的速度要大于三周台（图6）。在场地助滑距离和过渡区等相关变量不变的情况下，三周台面曲率半径和台高皆大于两周台，所以导致阻力的做功距离增加，对速度的递减作用也相应变大。由表6 可知，两周台比三周台出台速度平均高2 m/s。跳台角度发生改变，速度的变化同样是明显的，随着跳台面弧度增大，出台速度呈现递减趋势，当跳台弧度角每增加5°时，出台速度减小0.2 m/s。

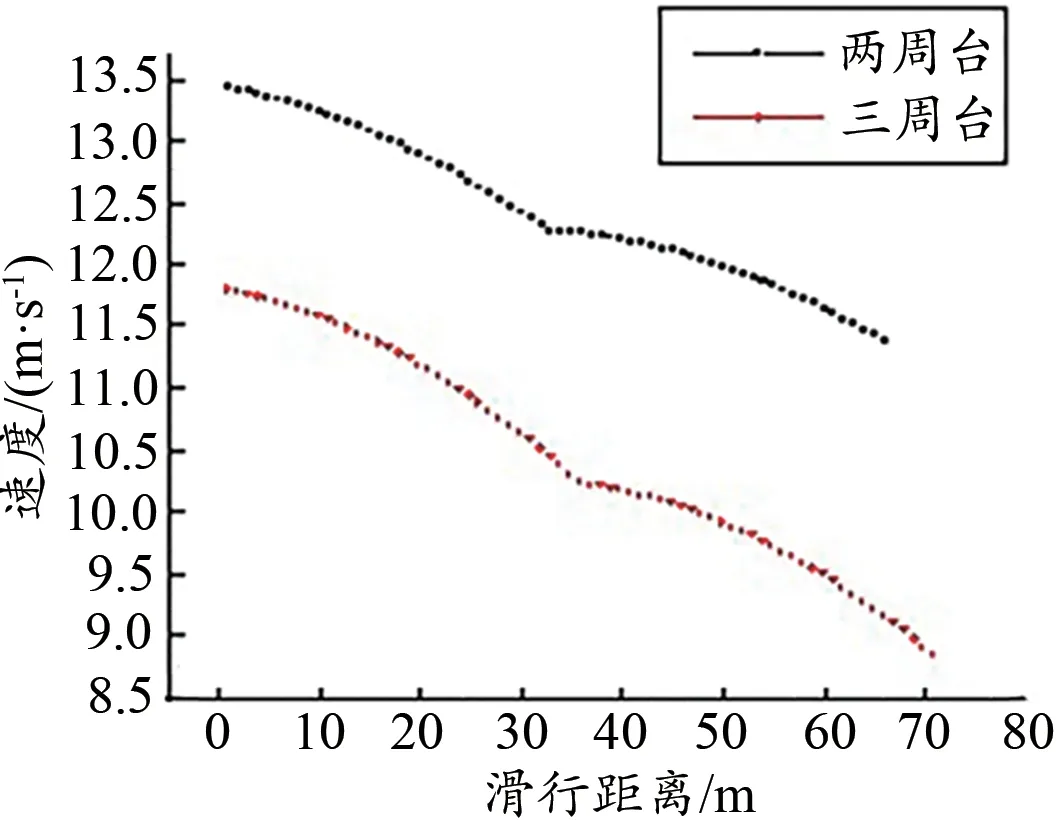
图6 场地跳台尺寸改变对出台速度的影响Figure 6.The Impact of the Size Change of the Platform on the Take-off Speed

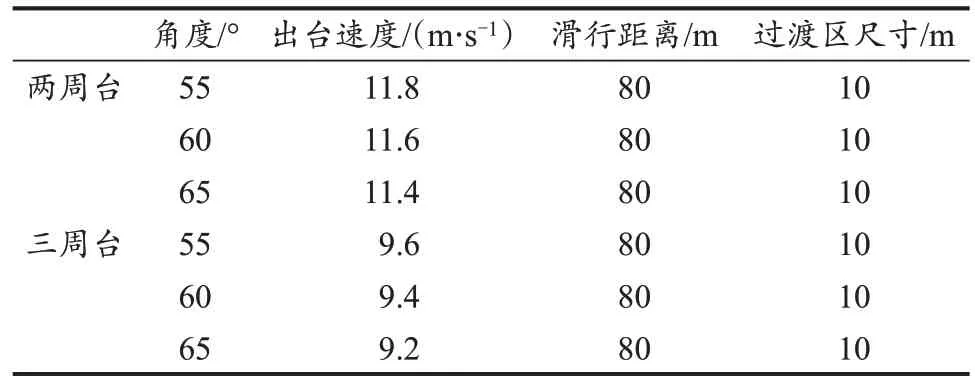
表6 跳台尺寸的高度和角度变化对出台速度的影响Table 6 Influence of Height and Angle Changes of Platform Size on the Launching Speed

2.3 数学模型的实验验证

选取5 名男子运动员三周台bFFF 动作（直体后空翻360°接360°接360°）和5 名女子运动员两周台bdFF（直体后空翻720°接360°）各6 次成功动作进行对比分析。为了控制其他变量的影响，数学计算模型中代入雪场实时环境参数和实际测量的运动员助滑距离和过渡区尺寸。运动员实际最大助滑速度根据雪场助滑坡架设的速度计测量获得，出台速度由录像解析获得，并与模型计算的数值进行对比。

本研究所采用方程获得的不同助滑距离和不同跳台的出台速度计算结果与真实影像数据分析结果比较接近，最大速度和出台速度皮尔逊分析结果为明显正相关，且具有显著性（r＞0.7，P＜0.05；表7，表8）。验证了本模型在充分考虑空气阻力、雪的摩擦系数和不同滑行姿势下，跳台尺寸变化对出台速度影响的数值分析正确性，这将为运动员和教练员根据不同场地制订动作方案起到量化的指导作用，减少试滑次数。

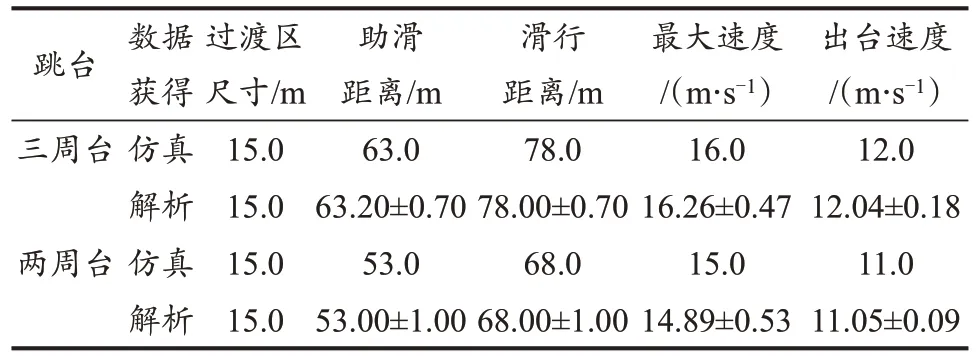
表7 仿真计算数据与影像解析数据对比Table 7 Comparison of Simulation Calculation Data and Image Analysis Data

表8 皮尔逊相关分析Table 8 Pearson Correlation Analysis n=10

3 结论与建议

3.1 结论

1）仿真跳台尺寸变化对出台速度的影响过程，显示在两周台、三周台最大速度和出台速度等主要参数上与实验数据均较为符合，呈显著正相关，证明了模型的有效性。

2）运动员在助滑坡上增加滑行距离，会增加出台速度，坡道上的滑行长度与出台速度呈正相关，且坡道上滑行距离增加了10 m 时，会使出台速度增加约1.1 m/s。

3）平坦的过渡区域长度与出台速度呈负相关，过渡区域长度每增加5 m，出台速度会降低3 m/s。

4）助滑距离和过渡区长度相同的情况下，两周台出台速度高于三周台2 m/s。随着弧度角的增加，出台速度逐渐减小，当跳台弧度角每增加5°，出台速度减小0.2 m/s。

3.2 建议

研究表明，跳台场地相关阶段尺寸变化会对运动员的出台速度造成影响，建议运动员与教练员在不同跳台场地进行训练和比赛前，首先对场地跳台尺寸进行了解和评估，同时注重跳台弧度的修整工作。在训练或比赛之前，建议运动员应充分进行测速以及滑台的适应工作，以初始测量的速度在起滑点按照所需完成动作的速度范围进行起滑点位置上的调整，使运动员的出台速度能够满足完成动作所需的滞空时间和起跳高度，进而高质量地完成整个动作。