大跨度钢管混凝土拱桥吊装施工线形监测方法研究

汪继芳 王艺

摘要：在大跨度钢管混凝土拱架吊装施工过程中，对主拱轴线的控制至关重要。文章基于测量控制原理及技术要求，提出一种拱桥吊装过程中线形监测方法——勾股定理函数求解法，并运用该方法计算得出各个观测点的坐标，与传统的“AUTOCAD描绘法”求出的精确坐标进行对比。结果表明：与传统方法相比，该方法原理清晰、操作简单易行，结果满足吊装线形监测精度要求，可为类似工程线形监测控制提供参考。

关键词：大跨度拱桥;吊装;线形监测;方法;可行性

0 引言

随着我国交通事业的飞速发展，高速公路已经成为各地经济社会交流的主要通道。特别是近年来我国实施西部大开发的发展战略，西部山区的交通也得到了快速发展，桥梁作为跨越障碍物、峡谷的重要结构物，人们对其跨度、美观性、环保性等方面的要求也越来越高。作为桥梁重要结构形式之一的拱桥，因其兼具跨度大，观赏性、经济性高及与环境协调统一等优点，在山区高速公路的建设过程中越来越受到设计工程师们的青睐。特别是在我国钢材大力发展的基础上，钢混组合结构因其材质轻、工作配合性好等优点在工程中已被广泛应用。而大跨度钢管混凝土拱桥囊括了以上优点，因而成为山区公路建设首选的跨越障碍物的结构。但山区环境条件恶劣、拱桥造型复杂，给施工带来较大难度，因而对于钢管拱肋在吊装过程中的线形控制成为其中一项重要的控制性技术[1]。现阶段进行大跨度钢管混凝土拱桥吊装施工时，缆索吊装-斜拉扣定技术较为常用，其线形采用监测每节钢管拱标高和拱轴线定位并借助扣索实施动态调整的方式来保证[2]。因此，吊装监测成为保证主拱按设计要求进行合龙的重要手段。

在劲性骨架吊装施工过程中，需在拱肋节段上布设合适的监测点对拱架进行定位[3-5]。为确保每节钢管拱吊装定位成功，应及时采集相关数据。本文以某钢管混凝土拱桥为工程背景，提出一种采用全站仪监测各拱肋节段上的棱镜观测点的方法，并通过实际施工验证其可行性。

1 工程概况

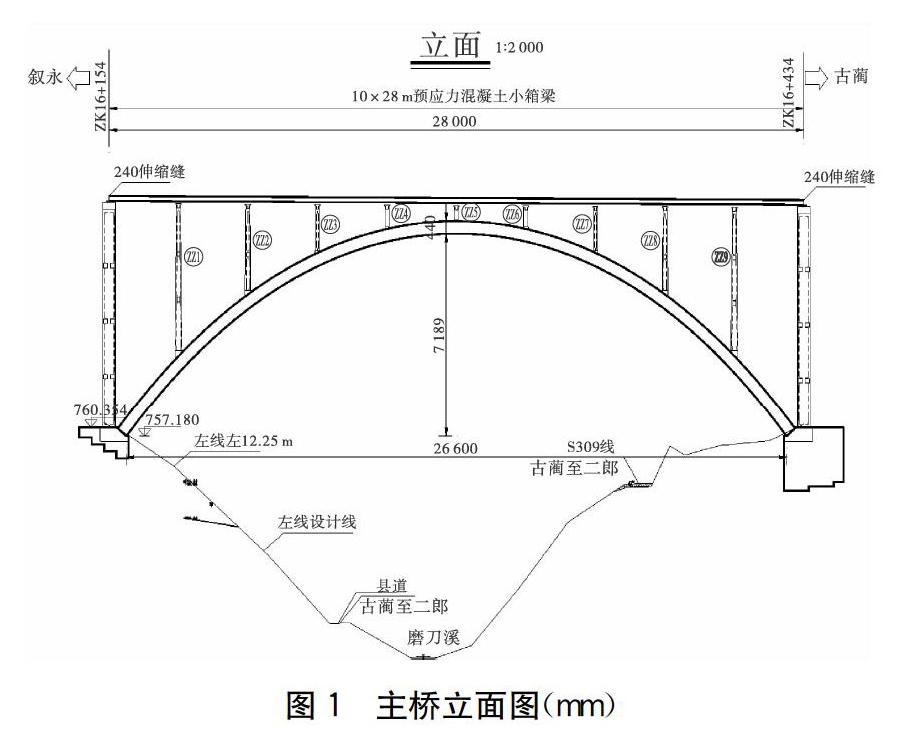
某大跨度钢管混凝土拱桥是叙古高速公路的关键性控制工程。该桥起于ZK15+838.00，止于ZK16+661.00，全长823m。跨径组合为：引桥（11×28）m[JP+1]的预应力混凝土箱梁+主桥280m（净跨径266m）的钢管混凝土拱桥+引桥（8×28）m预应力预应力混凝土箱梁。主桥上部结构为钢管混凝土劲性骨架上承式箱型拱桥，主拱为等截面悬链线无脚拱，拱轴系数m=2.2，净跨径266m，净矢跨比F0/L0=1/3.7。拱圈分左、右两拱肋，两肋间以横联连接，每肋为单箱双室截面，横向采用外形等宽7.6m，纵向采用外形等高4.4m，标准段顶、底板厚0.35m，腹板厚0.3m。拱圈拱脚至第一根立柱间为变厚段，顶板、底板混凝土厚度由0.65m线性变化至0.35m，边腹板厚度由0.5m线性变化至0.3m。主桥立面图见图1。

2 一种新的线形监测方法

2.1 传统的计算方法

采用传统的“AutoCAD描绘法”确定棱镜观测点精确位置坐标的计算方法的原理是：根据考虑预拱度的设计坐标值（10年收缩徐变+1/2移动荷载）及产生的变形总量的主拱肋制造线形的各节点坐标，利用AutoCAD软件做出通过各节点坐标的样条曲线，再根据上弦杆中心距钢管上表面的距离做出上弦拱圈表面的曲线，然后根据该曲线利用AutoCAD软件的捕捉功能，捕捉曲线上目标节点对应于上弦拱圈表面曲线处的切点，该切点即为棱镜坐标观测点与上弦杆表面垂直焊接点位置。最后做目标节点与切点的线段，并由切点向上延伸棱镜观测点距钢管表面的距离，则可得到棱镜观测点的精确坐标。对每个目标节点重复采用上述方法，得到其他目标节点对应的棱镜观测点精确坐标。传统的“AutoCAD描绘法”虽能得出棱镜观测点的精确位置坐标，但操作繁琐，需对每个节点描绘出其样条曲线，效率低下，且在进行捕捉时容易出现捕捉到错误节点的操作，造成误差。

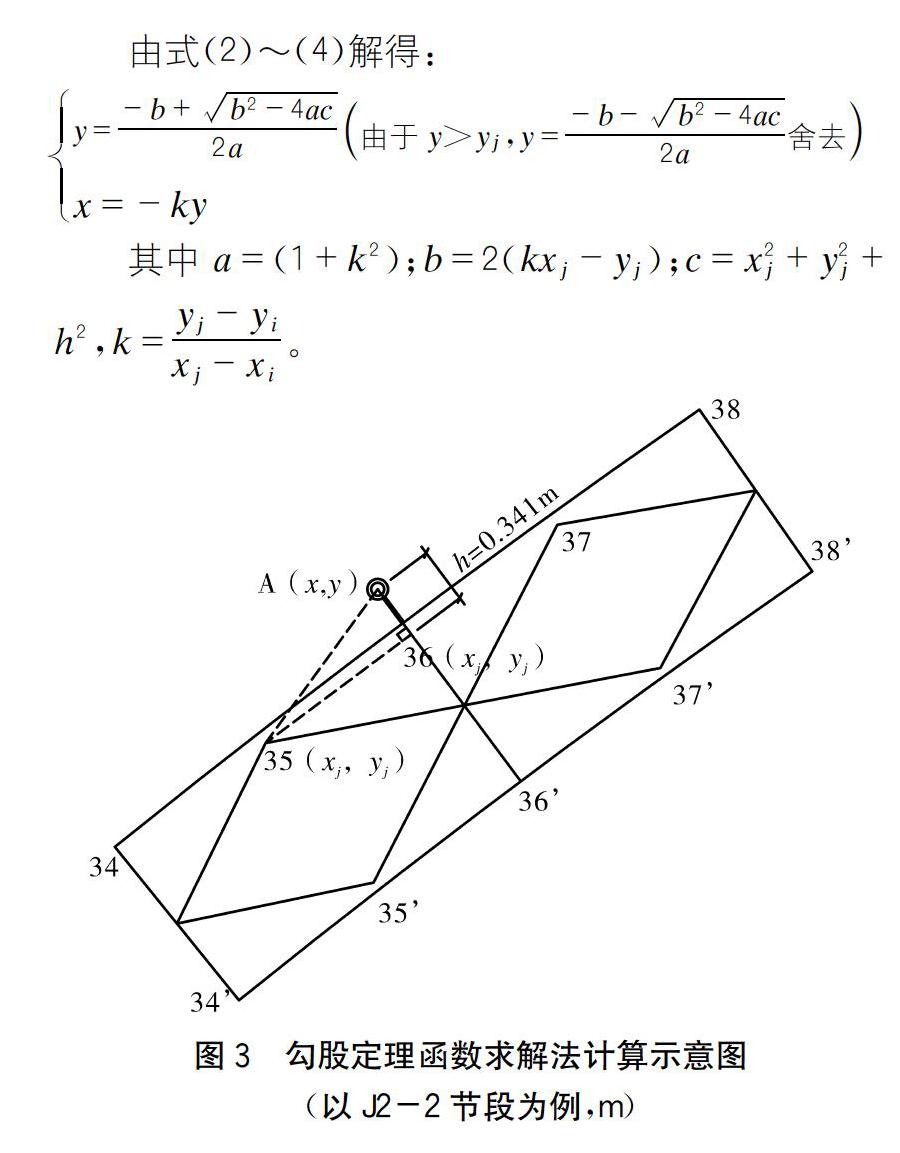
2.2 新的线形监测方法——勾股定理函数求解法

因传统的“AutoCAD描绘法”求解方法较为复杂，为便于计算，本文在基于拱肋相邻两节点之连线与目标控制节点和棱镜控制点之连线相互垂直的前提下，提出一种新的确定目标节点近似坐标的方法——勾股定理函数求解法。该方法是在已知两节点中心坐标值的情况下，利用事先测量出的棱镜控制点中央位置与其所在节点上弦杆中心位置之间的距离，可由直角三角形各边之间的勾股函数关系，运用Excel软件计算功能可得到各个目标节点对应的棱镜中央位置坐标。

以如图2所示的35节点、36节点（35为相邻节点，36为目标节点）为例介绍该线形监测方法的棱镜位置及棱镜精确位置（为方便展示，将上弦杆拱圈表面的曲线各位置处的曲率都已放大）。

由此可见，利用目标控制点与目标节点弦杆圆心的垂直距离，并在已知相邻两个节点所在弦杆圆心坐标的情况下，可根据勾股定理函数关系，求出控制测点棱镜中央坐标，并利用该坐标值对拱肋线形进行调整。利用以上函数关系，可通过Excel相关函数功能得到每个棱镜控制测点的坐标（x，y）。勾股定理函数求解法相对于传统的“AutoCAD描绘法”原理清晰，计算过程操作简单，大大提高了计算效率。

3 工程实例

3.1 观测点的布置

在对本工程劲性骨架吊装施工过程中实施拱肋监测控制时，均需于每个拱肋节段前端布设线形控制测点。布设控制监测点的原则是：吊装拱肋上单个节段前沿布设3个控制测点，每个棱镜六角中心点与上弦拱圈表面垂直距离为14cm，并在每节段上弦杆联结中心位置布设1个坐标观测点。1/2跨径节段钢管拱肋棱镜测点布置见图4，截面棱镜测点布置大样图见图5。采用焊接的方式将坐标观测点与弦杆表面固定，并采取措施保证两者垂直。在预制场地制作钢管拱肋的同时，根据监测要求在相应部位焊接安装棱镜作为线形控制测点，并采取安全措施进行保护，确保拱肋吊装监测时测点位置的有效性和准确性。吊装时，首先要保证棱镜测点与上弦杆表面垂直并牢固连接，确保两者间距始终不变。此时，采取调整棱镜控制点坐标值的方式达到控制钢管劲性骨架拱轴线线形的目的。

3.2 观测结果分析

根据该桥相关设计文件，上弦杆中心与钢管上表面之间的垂直距离为0.200m，棱镜中心点距上弦拱圈表面点垂直距离为0.139m，由此可知棱镜位置与目标节点上弦杆中心垂直距离为h=0.339m。通过该大跨度钢管混凝土拱橋各节点的施工立模坐标，利用式（4）可得到利用勾股定理函数求解法计算出的棱镜观测点近似坐标，并与采用传统的“AutoCAD描绘法”逐个求出的棱镜观测点精确坐标进行对比，结果见表1。

由表1可知，利用勾股定理函数求解法计算出的棱镜观测点近似坐标与传统的“AutoCAD描绘法”逐个求出的棱镜观测点，精确坐标之间的误差最大为0.002m，数据精度满足吊装线形监测精度要求。因此，该新方法求出的棱镜观测点坐标可作为本工程桥梁吊装线形监测的参考坐标。

4 结语

本文介绍了一种大跨度拱桥吊装过程中新的线形监测方法——勾股定理函数求解法，并通过工程实例，分析了新方法的计算坐标值与传统的“AutoCAD描绘法”逐个计算的监测点的精确坐标的误差。由以上对比分析，可得出如下结论：

（1）通过勾股定理函数求解法计算得到的坐标值可满足吊装线形监测过程中的精度要求，且方法原理清晰，计算简单，实施方便。

（2）由式（4）可知，当拱轴系数越大时，拱轴线曲率越小，采用勾股定理函数求解法计算得到的棱镜坐标值越接近精确值，方法精度越高。

参考文献：

[1]田军伟.大跨度钢管混凝土拱桥拱肋吊装施工控制[J].公路与汽运，2012（1）：164-166.

[2]张开银，刘三元，何雨微，等.大跨度钢管混凝土拱桥线形动态控制技术[J].武汉交通科技大学学报，2000（1）：1-4.

[3]樊秋林.主跨416m劲性骨架外包混凝土拱桥线形应力施工监控技术[J].铁道建筑技术，2013（12）：9-14，26.

[4]李自林，黄 辉，贾建国.戴河大桥拱肋施工线形控制技术[J].施工技术，2011，40（8）：78-82.

[5]黄顺利.钢管拱拱肋的吊装技术[J].中国新技术新产品，2011（7）：188-189.