平南三桥不同封拱脚方案对比分析
韦建昌 秦大燕 杜海龙
摘要:平南三桥为主跨575m的中承式钢管混凝土拱桥,其管径大、吊重大、吊装节段数多,如果采用传统的“先合龙,再封拱脚”的施工方案,会导致施工过程中线形和各扣索索力均匀性较差。为确定合理的封拱脚时机,确保施工安全,文章采用“过程最优,结果可控”一次张拉施工优化计算方法,从施工线形、扣索索力均匀性和拱圈应力等几个方面对三种封拱脚方案(单片拱肋两岸各吊装第四段后封拱脚、单片拱肋两岸各吊装第六段后封拱脚、单片拱肋两岸各吊装第八段后封拱脚)进行对比研究。研究结果表明,单片拱肋两岸各吊装第六段后封拱脚方案的施工线形、各扣索索力均匀性和拱圈应力等均较好,为最佳施工方案。基于此,对第六段封拱脚施工方式下拱圈实测线形和目标线形进行比较,进一步验证了施工方式的合理性。
关键词:拱桥;平南三桥;封拱脚方案;过程最优,结果可控;线形
0 引言
平南三桥为主跨575m的中承式钢管混凝土拱桥,其管径大、吊重大、吊装节段数多,如果采用传统的“先合龙,再封拱脚”的施工方案,会导致施工过程中线形和各扣索索力均匀性较差。为确定合理的封拱脚时机,确保施工安全,本文采用“过程最优,结果可控”一次张拉施工优化计算方法,从施工线形、扣索索力均匀性和拱圈应力等几个方面对以下三种封拱脚方案进行了对比研究:(1)单片拱肋两岸各吊装第四段后封拱脚;(2)单片拱肋两岸各吊装第六段后封拱脚;(3)单片拱肋两岸各吊装第八段后封拱脚。
1 项目概况
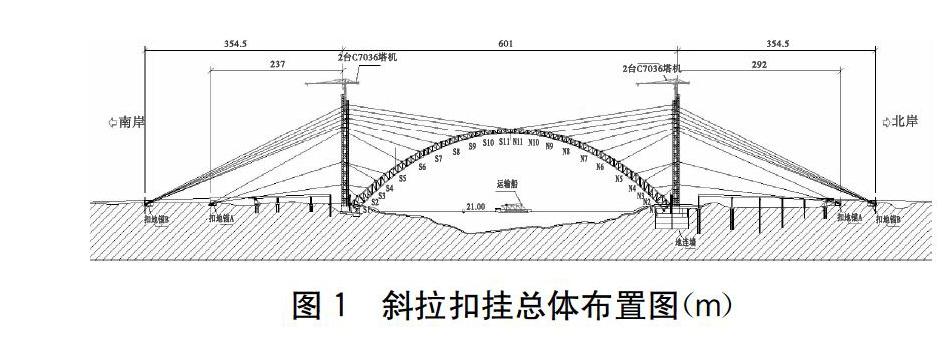
平南三桥为跨径575m的中承式CFST拱桥,矢跨比为0.25,拱轴线采用m=1.5倒悬链线。拱肋为变截面四肢桁架结构,每片拱肋分为22个节段吊装,总扣挂重量为9000t,最大节段吊装重量为220t,采用缆索吊运斜拉扣挂技术施工,采用每片拱肋连续吊装两节段横移一次的吊装方案[1-2],如图1所示。
整个吊装过程中采用对称吊装施工,吊装顺序如图2所示。对于大跨径拱桥而言,由于拱肋节段数多,采用吊装完所有拱肋节段再封拱脚的施工方式,即“先合龙,再封拱脚”,会使施工过程中的拱肋线形控制难度大,施工安全性较差。基于此,需选择合理的拱圈封脚方案,本文主要讨论三种不同封拱脚方案:(1)单片拱肋两岸各吊装第四段后封拱脚;(2)单片拱肋两岸各吊装第六段后封拱脚;(3)单片拱肋两岸各吊装第八段后封拱脚。选出最优方案以确保施工安全。
2 主拱圈施工控制
2.1 建模参数和荷载工况取值
采用大型有限元软件MidasCivil建模,拱肋节段和扣索分别采用梁单元和桁架单元建模,扣索采用1860MPa15.2mm高强度低松弛钢绞线,弹性模量E=1.95×108kN/m2,其余各几何参数、材料参数以及扣索长度的等效处理见文献[2]。MidasCivil软件建模中拱肋钢材容重取为83.22kN/m3,经计算,平南三桥主拱钢材换算容重为1.06。各拱肋节段质量统计如表1所示。
2.2 计算方法
现有钢管混凝土拱桥施工控制方法主要有零弯矩法[3]、迭代法[4-5]、无应力长度法[6-7]和基于影响矩阵原理的优化算法[8-9]等。零弯矩法视拱肋各节段的连接为脚接,基于力矩平衡原理计算各扣索索力。该方法计算原理简洁、高效,但忽略了吊装的切线拼装位移,且计算得到的扣索力有时会出现负值,导致扣索力计算失真。李传夫、李术才等[5]以湖北某计算跨径为430m的钢管混凝土拱桥为工程背景,将最优化计算理论引入正装迭代法中,以此计算拱圈施工各扣索索力。徐岳、申成岳等[4]基于影响矩阵原理和正装迭代计算理论,提出了改进迭代法,并将该计算理论应用于跨径为248m的钢管混凝土拱桥中,较传统正装法提高了计算效率。李开心、龚清盛等[7]将无应力长度计算理论推广应用于钢管混凝土拱桥的斜拉扣挂施工,并取得较好的计算效果。由于传统的施工控制计算方法仅控制合龙松索后的线形,忽略了拱圈安裝施工过程中的线形和索力均匀性等问题。韩玉、秦大燕等[8]基于影响矩阵原理和最优化计算理论,以合龙松索后线形为约束条件、各吊装施工阶段线形为优化目标函数,建立拱圈一次张拉施工优化计算方法。该方法应用于跨径320m的钢管混凝土拱桥——马滩红水河特大桥的施工控制,通过与实测数据对比,验证了该计算方法具有良好的计算精度[8][10]。流程图详见图3。
3 传统封拱脚方案
传统钢管混凝土拱桥施工多采用“先合龙,后封拱脚”的施工方案,对于小跨径拱桥而言,具有较好的适应性,而对于吊重大、拱肋节段数多的大跨径拱桥,施工线形控制难,施工风险较大。基于此,本文以平南三桥为工程背景,采用文献[8]提出的一次张拉施工优化计算方法,对“先合龙,再封拱脚”的施工方案开展研究。
3.1 拱圈线形
经过计算发现,拱圈上游(A)和下游(B)以及南北两岸索力和各控制点线形差别小,因而取南岸下游计算分析。取合龙松索后线形偏差为30mm,施工过程中各控制点线形偏差如图4所示。从图4可以看出,采用“先合龙,再封拱脚”的施工方式,施工过程中各控制点线形与目标线形偏差达到382mm,施工风险大。
3.2 各扣索索力均匀性
进一步地,对拱圈施工过程中,各扣索均匀性进行计算,计算结果见图5和图6。由图5和图6可知,拱圈施工过程中,各扣索索力变化较大,最大变化值达到300kN(4#扣索力),导致施工风险较大。
4 不同封拱脚方案对比分析
由以上分析可知,采用传统的“先合龙,再封拱脚”的施工方案,将导致施工过程中的线形和各扣索索力均匀性较差,施工风险较大。因此,需选择合理的封拱脚时机。基于此,对以下三种封拱脚方案进行
建模计算,分析各扣索索力均匀性、施工线形和拱圈应力等情况:(1)单片拱肋两岸各吊装第四段后封拱脚;(2)单片拱肋两岸各吊装第六段后封拱脚;(3)单片拱肋两岸各吊装第八段后封拱脚。
4.1 各扣索索力对比分析
(1)各扣索索力均匀性
由图7(a)可知,各封拱脚方案相邻两扣索索力均在100kN以内波动,各扣索索力变化平缓,均匀性较好。
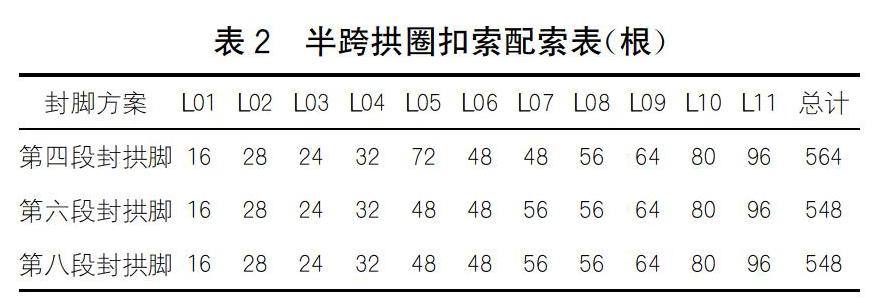
(2)最大扣索力及配索(见表2)
由图7(b)可知,在整个吊装施工过程中,第六段封拱脚和第八段封拱脚相邻两索力均变化在200kN范围内,索力均匀性好。采用第四段封拱脚方案,第5号扣索和第6号扣索相差327kN,存在较大波动性。表2进一步表明,采用第四段封拱脚方案所需扣索数量略高于其他两种封拱脚方案。
4.2 线形对比分析
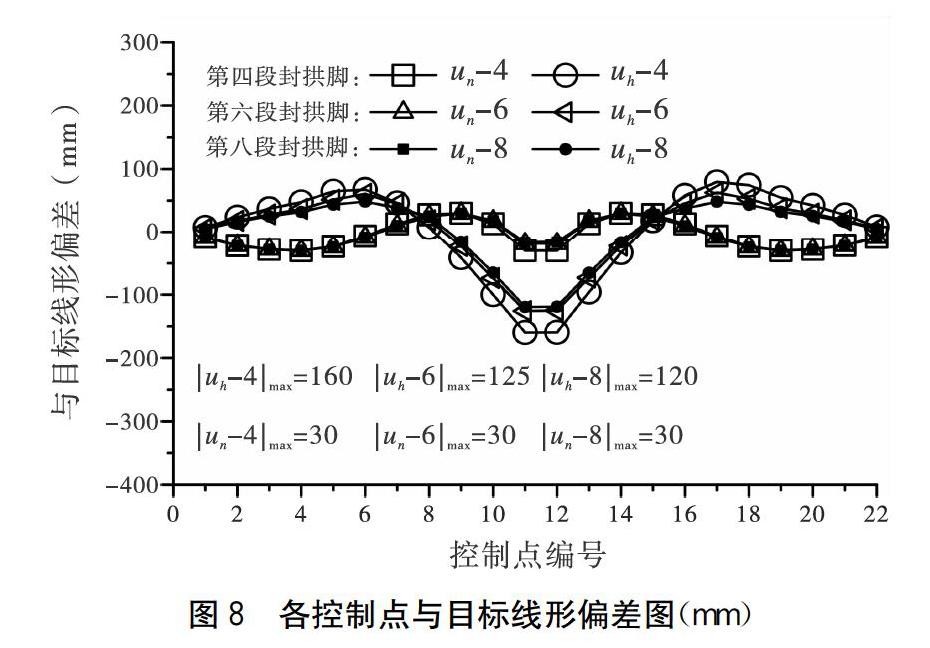
[JZ][XCLL68.EPS;P][TS(][HT9.H][JZ]图8 各控制点与目标线形偏差图(mm)[TS)]
由图8可知,在整个吊装施工过程中,三种封拱脚方案施工过程中线形与合龙松索后线形均合理。从线形精度考虑,第六段和第八段封拱脚方案的线形要优于第四段封拱脚方案。
4.3 白噪音试验
引入幅值为30mm的白噪音,进行了200次试验分析,其试验结果如图9所示。
由图9可知,采用第四段封拱脚方案,引入幅值30mm的白噪音,开展200次误差实验分析,在松索成拱后分别被放大成为44mm,具有一定的施工风险。
5 结语
(1)三种封拱脚方案索力均匀性均较好,第六段封拱脚和第八段封拱脚方案各扣索配置数量相同,略低于第四段封拱脚方案的扣索数量。
(2)通过白噪音试验研究表明,第六段封拱脚方案和第八段封拱脚,变化幅度均很小。第四段封拱脚方案引入幅值为30mm的白噪音,在松索成拱后分别被放大成为44mm,具有一定的施工风险。
在整个吊装施工过程中,第四段封拱脚方案的线形、索力均匀性以及经济性均不及第六段封拱脚方案和第八段封拱脚方案,第六段封拱脚方案和第八段封拱脚方案的扣索数量、索力均匀性、线形精度均很接近。由于提前封拱脚有助于提高后续施工过程中的安全性,因此,实际施工采用单片拱肋两岸各吊装六段后封拱脚。
参考文献:
[1]韩 玉,杜海龙,秦大燕,等.平南三桥施工重难点及关键技术研发[J].公路,2019(10):140-146.
[2]秦大燕,杜海龙,韩 玉,等.超大跨径拱桥不同吊装方案对比分析[J].公路,2019(12):100-104.
[3]周水兴,江礼忠,曾 忠,等.拱桥节段施工斜拉扣挂索力仿真计算研究[J].重庆交通大学学报(自然科学版),2000,19(3):8-12.
[4]徐 岳,申成岳,朱谊彪,等.确定拱桥斜拉扣挂施工扣索张力的改进迭代算法[J].桥梁建设,2016,46(2):65-69.
[5]李传夫,李术才,魏建军,等.迭代优化算法在大跨拱桥线形控制中的应用[J].山东大学学报(工学版),2008,38(3):23-27.
[6]谭 俊.无应力状态控制法在桥梁施工控制中的应用[J].公路,2016(4):122-126.
[7]李开心,龚清盛,田维锋,等.拱桥缆索吊装施工的无应力状态控制法[J].中外公路,2012,32(6):203-207.
[8]韩 玉,秦大燕,郑 健.CFST拱桥斜拉扣挂施工优化计算方法[J].公路,2018(1):100-104.
[9]崔凤坤,朱谊彪.基于影响矩阵的钢管混凝土系杆拱桥成桥吊杆内力的优化[J].中外公路,2015,35(6):195-199.
[10]韓 玉,秦大燕,杜海龙.一次张拉优化算法在大跨径CFST拱桥线形控制中的应用[C].中国公路学会桥梁和结构工程分会2019年全国桥梁学术会议论文集,2019.
[11]GB50923-2013,钢管混凝土拱桥技术规范[S].

