Event-Triggered Sliding Mode Control for Trajectory Tracking of Nonlinear Systems

Aquib Mustafa,, Narendra K. Dhar, and Nishchal K Verma,

Abstract—In this paper, an event-triggered sliding mode control approach for trajectory tracking problem of nonlinear input affine system with disturbance has been proposed. A second order robotic manipulator system has been modeled into a general nonlinear input affine system. Initially, the global asymptotic stability is ensured with conventional periodic sampling approach for reference trajectory tracking. Then the proposed approach of event-triggered sliding mode control is discussed which guarantees semi-global uniform ultimate boundedness. The proposed control approach guarantees non-accumulation of control updates ensuring lower bounds on inter-event triggering instants avoiding Zeno behavior in presence of the disturbance. The system shows better performance in terms of reduced control updates, ensures system stability which further guarantees optimization of resource usage and cost. The simulation results are provided for validation of proposed methodology for tracking problem by a robotic manipulator. The number of aperiodic control updates is found to be approximately 44% and 61% in the presence of constant and time-varying disturbances respectively.

I. INTRODUCTION

C ONVENTIONAL control theory is usuallybased on time triggered approach,i.e., periodic sampling of feedback and accomplishment of control law. This approach is well known for its simplicity of analysis. In this approach rate of control law execution does not depend upon system states.Such control approach may be inefficient from computational perspective. An alternate approach known as an eventtriggered control has been presented in [1]. In event-triggered control, execution of control law is done in aperiodic manner.The control input is computed at events based on condition(s)or threshold value(s) which relies on evolution of system states. Hence, the number of data packets transmitted over network are less which in turn reduces actuator efforts. Eventtriggered control makes optimal utilization of resources and improves performance in terms of processing time. Simple event-triggered control approaches have been presented in[2]-[4]. Lunzeet al.show state feedback based eventtriggered control in [5]. Several works in distributed network control system, decentralized sensor networks, consensus control with time delay on event-triggered approach can be referred to [6]-[14]. The works presented in [15], [16] discuss non-linear event-triggered approach.

The uncertainties are unavoidable in real-time control systems. They might adversely affect the performance of system. Hence, their treatment becomes a necessary task. The current state-of-the-art primarily deals with event-triggered strategy for systems without uncertainty or some works have been reported on linear system with uncertainty [5], [12], [13].Uncertainties in system affect the performance of eventtriggered control [5].

To overcome uncertainty present in system, sliding mode control (SMC) has been used for its good performance [17]-[19]. SMC can be used for continuous as well as discrete time system dynamics. For discrete time SMC, steady-state performance of system depends upon sampling time and disturbance bound [20]. Liet al.in [21] have designed an adaptive sliding-mode stabilization for Markov jump nonlinear systems with actuator faults which guarantees stochastic stability of closed loop system. These works are based on conventional time-triggered approach. Event based SMC have been presented in [13], [22] for linear system.These works do not cater to admissibility of control inputs.Admissibility in event-trigger is defined by a bound on inter execution time for update of control law which should be a finite value to ensure system stability. Ferrara and Cucuzzella[23] have shown general results for sliding mode control of first and second order using event-based approach. The paper considers triggering conditions first and then goes for stability analysis of the system in both cases. The triggering conditions are designed using threshold values which are arbitrarily set.

The motivation for this work is to develop an approach which reduces usage of various resources and actuator efforts.In addition to it, a controller methodology should take care of system stability, uncertainty and admissibility of control executions. SMC has been extensively studied in recent years but to the best of our knowledge there is dearth of work which analyzes the performance of SMC for trajectory tracking by nonlinear system based on event-triggered approach. This paper puts an effort to present such a controller design by considering the dynamics of robotic manipulator and modeling it into a general nonlinear control affine system. The event-based approach performs at par to the time-triggered controller if not better. The work done in this paper can be summarized into following contributions:

1) The event-triggering condition is derived using Lyapunov theory which ensures accuracy and stability of SMC.

2) Admissibility or bound on inter-execution time has been derived for controller application.

3) The controller design considers uncertainty in nonlinear system dynamics.

The paper is organized as follows. Section II presents preliminaries. Section III has three subsections. The first subsection presents mathematical modeling and sliding mode control law design for trajectory tracking. The proposed event-triggered sliding mode control law is discussed in second subsection. The third subsection discusses semi-global uniform ultimate boundedness of dynamical system on desired trajectory ensuring minimum bound on inter-event time. In Section IV, results and discussions for trajectory tracking have been presented. Finally, conclusions are drawn in Section V.

II. PRELIMINARIES

A nonlinear input affine system with external disturbance is considered as

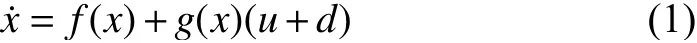
The control input depends on tracking error and desired trajectory. The control law can therefore be written as a function of γ , i.e., α (γ).

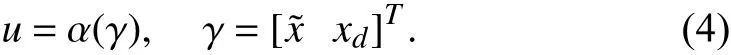
The tracking error dynamics is further expressed as

The event driven approach updates control law in an aperiodic way on the basis of triggering condition(s). An event is basically a discrete time instant when system tends to become unstable and a necessary action is to be taken to make it stable. The necessary action here is the update of control input (u) which ensures stability of the system along with the desired trajectory tracking. The control law is updated at nonuniform time instantti(i=0,1,2,....). If the system remains stable then there will be no triggering of event and consequently there will be no update of control input. The tracking error dynamics can be expressed in terms of eventbased control input as

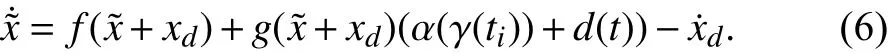
A parameter termed as event-trigger error (e) is defined for developing triggering condition.

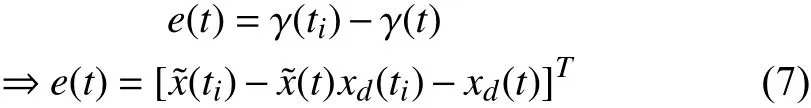
wheret∈[ti,ti+1). The event-trigger error (e) is different from trajectory tracking errorThe objective of defining the event-triggered error in terms of tracking errorand the known desired trajectoryxdis to design the event-triggering condition from Lyapunov stability analysis. The desired trajectoryxdis known but it is time varying by nature. The difference (i.e. error) between the desired value ofxdat last triggering instant and current time instant contributes in deciding events based on stability of the system. Equation (6) can be further expressed as a perturbed dynamics in terms of eventtrigger error.

The following section provides a novel approach for design of event-triggered SMC for nonlinear input affine system with external disturbances.

III. SYSTEM MODELING AND CONTROL LAW FOR TRAJECTORY TRACKING

The proposed control approach has been designed by modeling the dynamics for a class of nonlinear system into a general nonlinear control affine system. The control approach can be directly applied to system which are already in affine form.

A. Nonlinear Control Affine System

The dynamics of a class of continuous time system is described mathematically in the following non-linear differential form [24], [25].

wherenis number of states,q∈Rnis position vector,is velocity vector,M(q) isn×ninertia matrix,andG(q)aren×1 are system vector,is uncertainty term and τ(t) isn×1 control vector.

For controller design, the dynamic model given in (9) has to be expressed in standard nonlinear control affine form with respective states. The position and velocity vectors considered here are as follows.

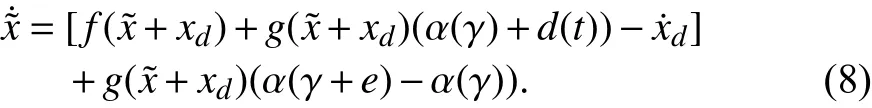
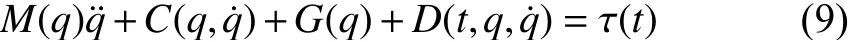
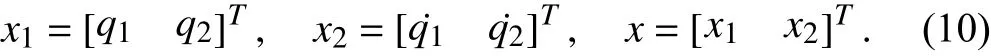
The system parameters and control input are expressed as

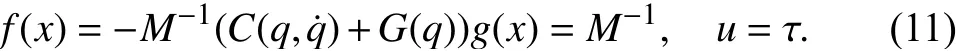
Using (10) and (11), the state space model for (9) can be written in following form.

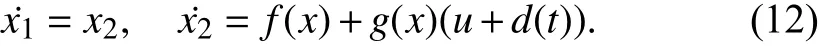
The control law designed for tracking is based on SMC. A sliding surface (S(t)) is defined in terms of tracking errorand

where λ is a non-zero positive sliding gain parameter withandandx2drepresent the states of respective desired trajectories. The derivative of sliding surface can be expressed as

A Lyapunov functionVis defined in terms of sliding surface.

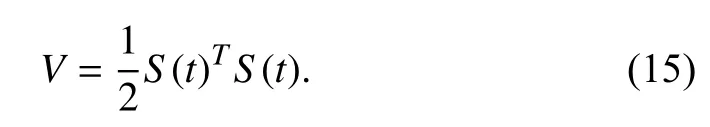
Using (12) and (14), the derivative of Lyapunov function defined in (15) is

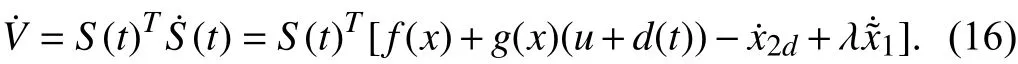
For a non zero positive constantK, closed loop system will be stable for the control law designed as

whereη is a non zero positive constant. The derivative of Lyapunov function in (16) will become

Equation (18) proves that the sliding mode control law in(17) ensures asymptotic stability of system. Event triggered approach for SMC is discussed in following subsection.

Remark 1: Note that, for the control law in (17) with a positive scalar constant η, system given in (12) converges to zero and guarantees stability in presence of disturbance.

Remark 2: The notion of zero dynamics of a nonlinear system is used in the investigation of three classes of problems that arise in robotics: control of robots in rigid contact with the environment, free motion control of manipulators with redundant degrees of freedom, and trajectory control of robot arms with flexible links. In each case, the internal dynamics present in the system when a proper output is constrained to be zero is characterized, and a physical interpretation of such dynamics is provided [26].

B. Event Triggered Sliding Mode Control

In this subsection, design of an event-based control law and triggering conditions are discussed. The control law should meet following two aspects:

1) tracking error should converge to zero ensuring asymptotic stability of system, and

2) does not violate admissibility condition, i.e., non stacking of actuator actions.

The following assumptions are considered for design of event-triggered SMC law applied to system (12) for trajectory tracking problem.for system given in (5), such that for allxd

Assumption 1: Consider a Lyapunov candidate function

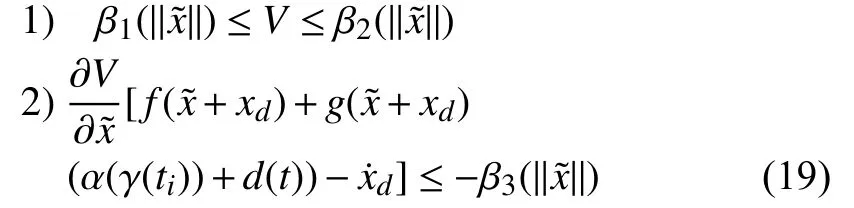
where β1(·), β2(·) and β3(·) are classK∞functions.

Assumption 2: The functionsf(.) andg(.) of system dynamics are assumed to be known.

Assumption 3:f(·),fd(·),g(·), α(·) are assumed to be Lipschitz [27] on compact sets.

Assumption 4: ∀t≥0,, | |xd||≤hand ||d(t)||≤dmaxwhere, σ ≥0,h≥0 anddmax≥0 [28].

Assumption 5: Variation ing(x) over triggering instant i.e.the intervalt∈[ti,ti+1) is negligible.g(x) is positive definite and bounded by maximum value ofLgon compact setE[24].

Remark 3: The sliding mode variable, controller design, and event-triggering condition takes into accountfandg. Hence,this work considersfandgto be known. Thefandgmay be considered uncertain as in [29].Remark 4: As per [24], a non-linear dynamical system can be modelled in state space form whereg(x) represents the inverse of inertia matrix. For such a systemg(x) is positive definite and bounded by maximum value ofLgon compact setE. For the sake of simplicity, variation ofg(x) during interevents, i.e., the intervalt∈[ti,ti+1) are assumed to be negligible.α(.) on compact set

A Lipschitz constant, denoted asL, is defined for function Using Assumption 2 with equation for (4), one has

Theorem 1: Let an event-triggered sliding mode control law for system in (12) can be designed as

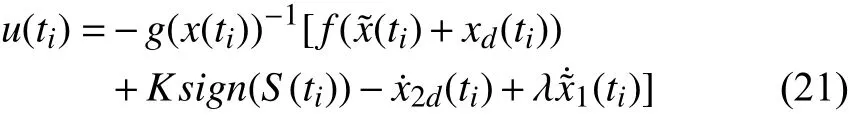
wheretirepresents a triggering instant. If the following threshold conditions

whereeis defined in (7),

whererris a design parameter which guarantees boundedness of tracking error are not satisfied, then an event is triggered and control input is updated. The gradual triggering of events lead tracking error to converge to zero in presence of disturbance and the system shows asymptotic stability.

Proof:Consider a Lyapunov functionas per of Lyapunov function can be expressed aswhich Assumption 1 for the system described in (12). The derivative can be further expressed using perturbed dynamics in (8) as

Using Assumption 1, (22) can be expressed as

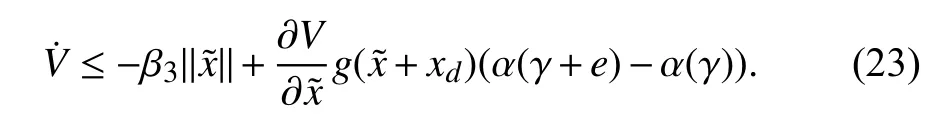
Consider the second term of (23) for further analysis

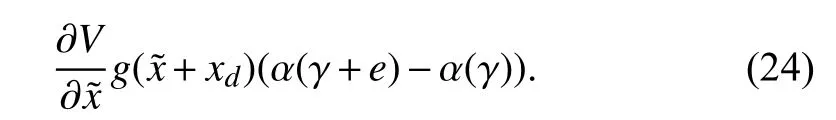
The Lyapunov candidate function is explicitly defined as

The partial derivative ofcan be expressed as

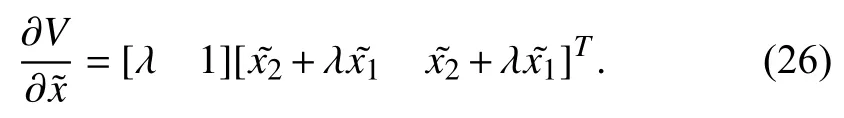
Using Assumption 4,

Using (17) and (21) along with Assumption 4 at eventtriggered instantti, (27) can be expressed as

Equation (28) can be further written using (2) as

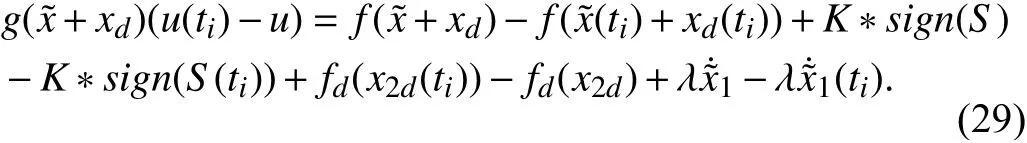
As per Assumption 2,f(·) andfd(·) are assumed to be Lipschitz for a defined set. Hence,

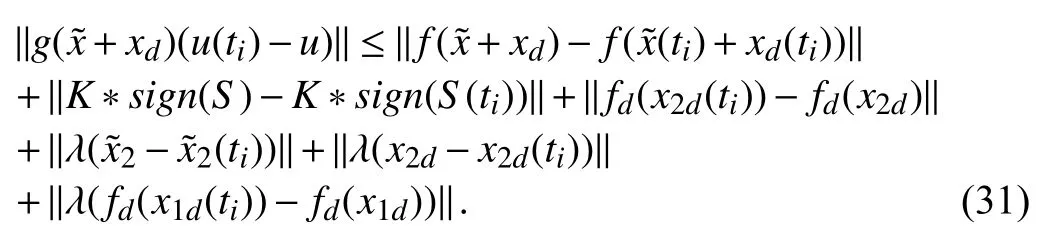
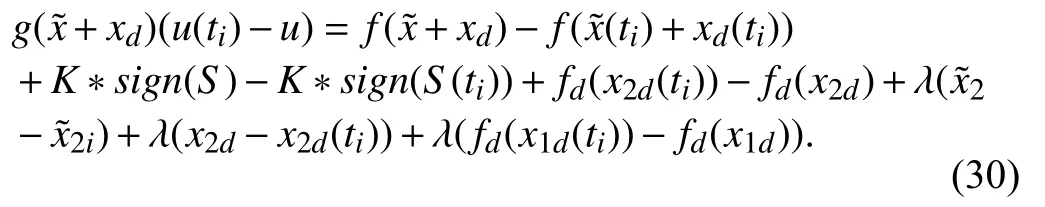
Equation (31) is further expressed as

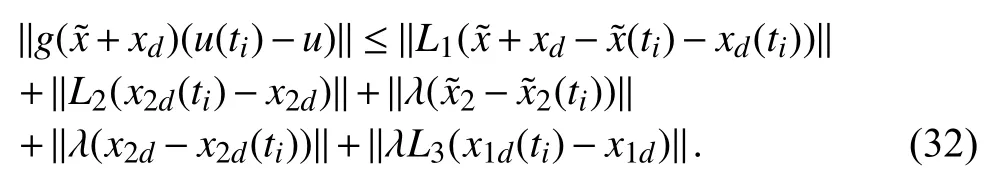
Equation (32) is written below in terms of event-trigger error ‖e‖.

where event-trigger error (e) is given in (22a). Equation (33)is further expressed as

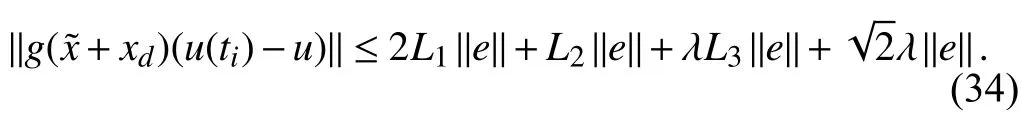
Using (26) and (34), equation (24) can be written as

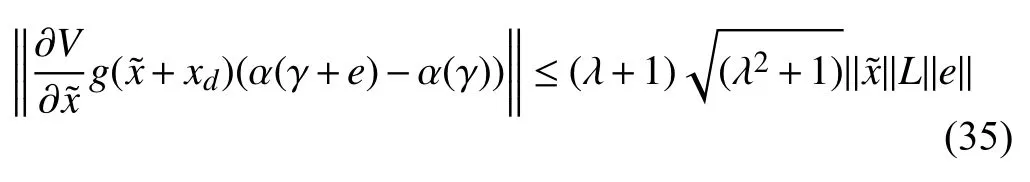
where

Using (18) and (35), equation (22) can be further written as

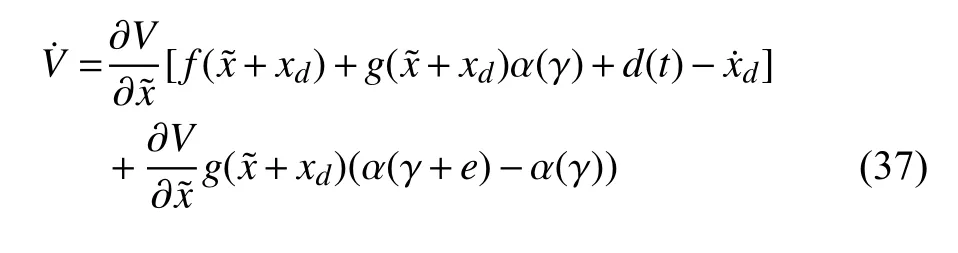
which will finally become

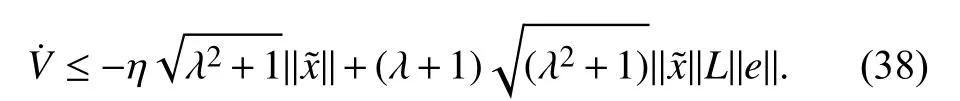
Using the event-trigger threshold condition (22a) in (38),one can ensureIt shows that the system in (12) with the designed control law in (21) is bounded and achieves convergence despite the disturbance. The violation of threshold conditions (22a) and (22b) are necessary as well as sufficient for the update of event-driven sliding mode control.This completes the proof of Theorem 1.

Remark 5: Theorem 1 shows that control law in (21) will force the system to track the desired trajectory in presence of disturbance rendering asymptotic stability of the system. The proof ensures this approach can be applied to real-time applications with resource optimization.

C. Admissibility of Event-Driven Control

The admissibility of event-driven control law is necessary to avoid the piling of triggering instants and ensuring the stability of system. Theorem 2 provides a lower bound for an inter-event triggering interval.

Definition 1: Admissibility in event-triggered system is defined as the inter-execution time for update of control law which is always lower bounded by a finite value.

Lemma 1 (Comparison Lemma) [27]:Let the scalar differential equationwheref(t,v) is locally Lipschitz invand continuous int, ∀t≥0 andv∈W⊂R. Consider [t0,T) be maximal period of solutionv(t),and assume thatv(t)∈W∀t∈[t0,T) . Considerm(t) be aD+m(t) satisfy differential inequalityD+m(t)≤f(t,m(t)),m(t0)≤m0withm(t)∈W∀t∈[t0,T). Then,m(t)≤v(t) for allt∈[t0,T).continous function whose upper derivative on right-hand

Theorem 2: For the system in (12), event-driven control is updated on violation of conditions in (22a) and (22b)∀ti(i=0,1,2...). For admissibility of system the inter-event periodTidefined asTi=ti+1-tishould always be lower bounded by a positive constant given by

Proof: The time required for event-trigger error ‖e‖ to rise from zero at last triggerng instant to threshold value should be lower bounded. Hence, the accumulation of triggering instants and existence of Zeno phenomenon can be avoided ensuring a stable system. The event driven system is represented as

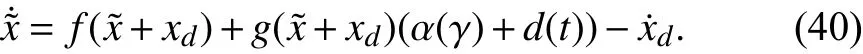
Using triangular inequality, (40) can be expressed as

Fora Lipschitz constantLais defined on compact setEbased on Assumptions 2 and 3. Equation (41) therefore becomes

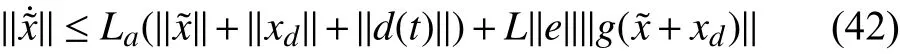
There exists a constantQ(Q＞0) such thatAs per Assumption (3)

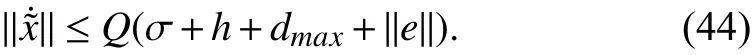
For the rate of change of event-trigger error,

Then, using Lemma 1

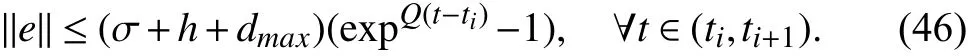
Using (22a) in (46) the lower bound on inter-event time is obtained as

Remark 6: Theorem 2 shows that the inter-execution time in(47) for the designed control law (21) will be lower bounded.The boundedness on inter-execution time will ensure nonaccumulation of actuator actions and further guarantees robust trajectory tracking. This proof supports the real-time feasibility of developed resource optimization approach.

Remark 7:Lis computed using (36). For choosingLj(j=1,2,a,...)(Lipschitz constant), it is necessary to have a set( β1and β2are defined in Assumption 1) where forR≥0, the setS(R)includes all system statesFor allwith bounded initial condition to enter the setS(R) in finite time and to stay there,the tracking erroris uniformly ultimately bounded by the closed ball of radius

The value ofQdepends onLa,Lg, andL.LaandLare Lipschitz co nstants andLgis the maximum value ofg. The variablesand ‖e‖ in (43) are positive scalar values. Hence, the values ofLa,Lg, andLare chosen such that they at least satisfy

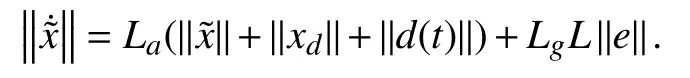
The above equation can be expressed in the form of a standard equation of a planewhere

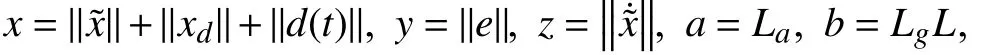
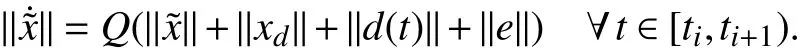
The equation above can also be expressed in the form of a plane, wherea=Q,b=Q, andc=-1. The values ofLa,Lg,andLare chosen prior toQ. Hence, the value ofQis chosen based on the space/domain where these two planes either intersect or overlap keeping the (44) intact. There is an alternative to compute minimum inter-event time for the proposed approach. One can always express the minimum inter-event time expression based on the parametersLa,Lg,andLand maximum values ofand ‖d(t)‖.

IV. RESULTS AND DISCUSSIONS

This section validates the proposed event-triggered sliding mode controller for trajectory tracking problem. Simulations are carried out for two-link robotic manipulator. The dynamics is given by

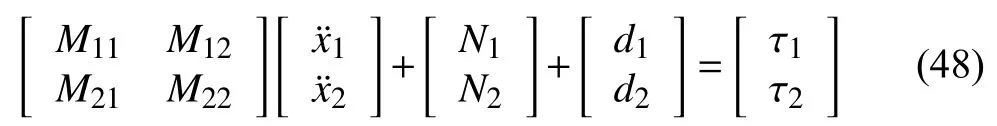
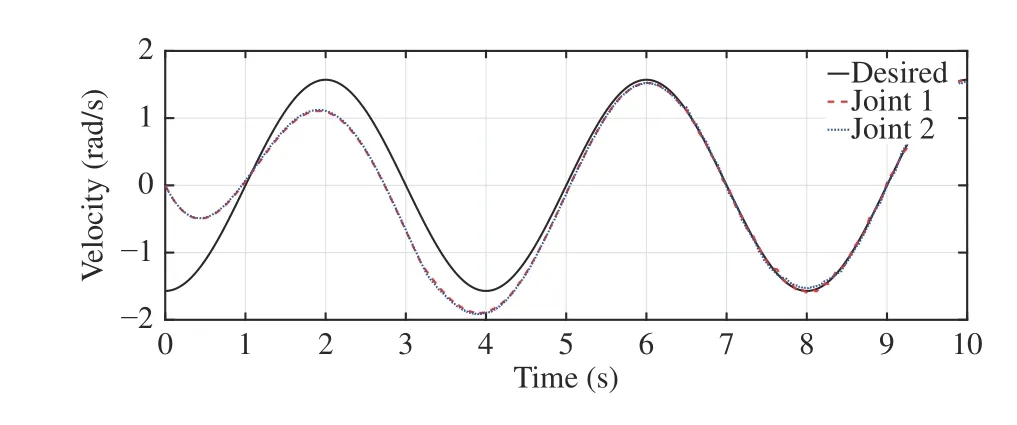
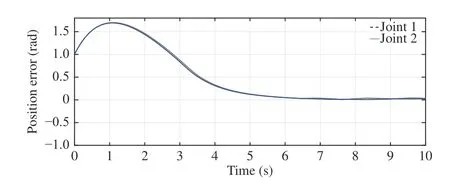
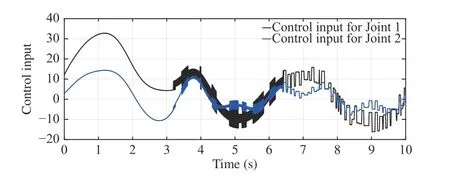
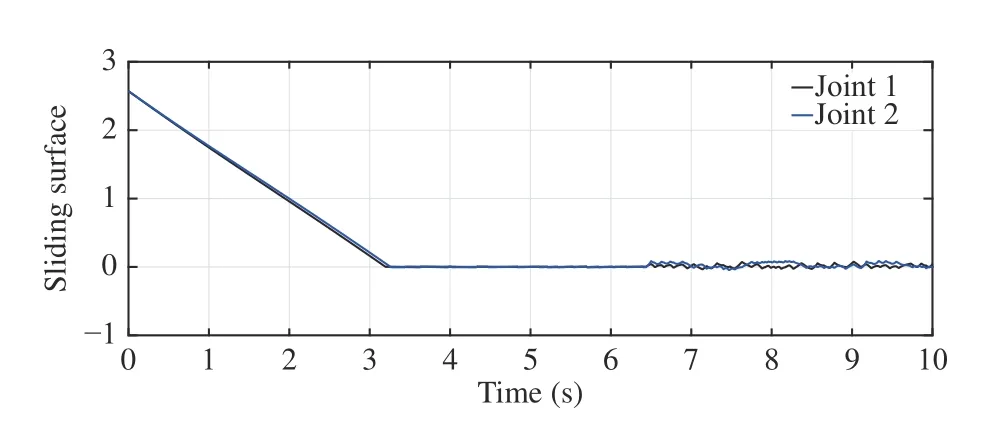
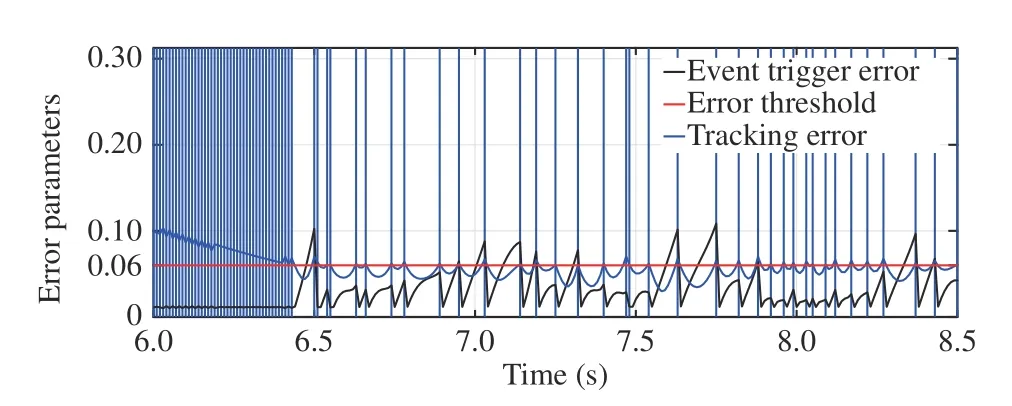
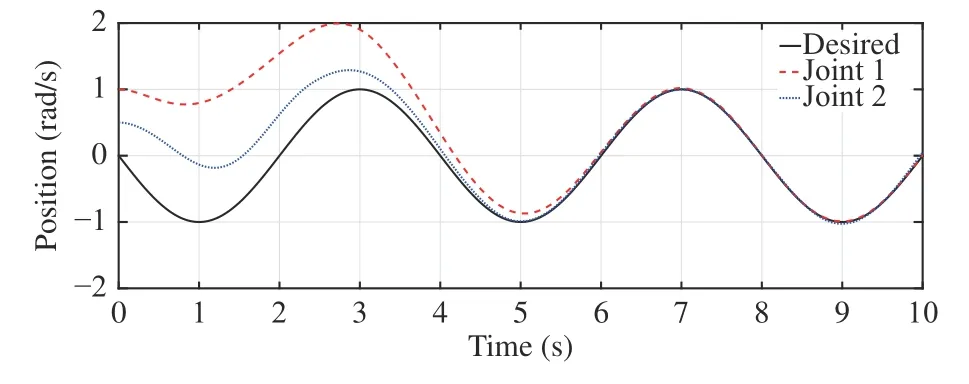
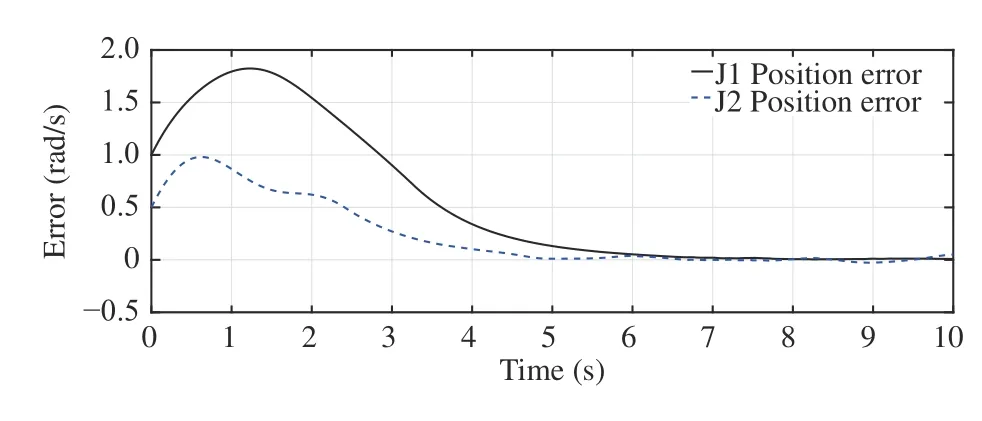
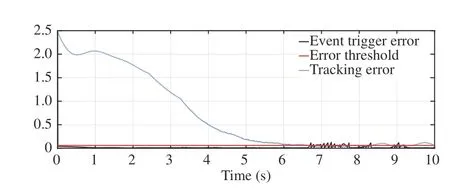
whereandLumped Coriolis and Gravitational force is represented bysin(x2)+(m1+m2)ga1cos(x1)+m2ga2cos(x1+x2) andcos(x1+x2)for joints-1 and 2 respectively.d1andd2represent disturbances and τ1and τ2are torques for joints-1 and 2, respectm1= 1 kg,m2= 1 kg,a1= 1 m anda2=1 m. (m1,m2) and(a1,a2) are mass and length of links respectively.The desired trajectories for two joints arexd(t) = [c os(1.57t) cos(1.57t)]T.ively. The structural parameters of robotic manipulator are:The initial joint positions arex(0) = [ 11]T. The Lipschitz constantLis determined using (36) as 0.85. The sliding mode gain parameter λ in (13) is considered to be unity. Consider the design parameter η = 0.7 and bound on tracking errorr=1.2. The sampling period considered is 0.01s. The results have been obtained for constant as well as time-varying disturbances in the system. The initial results are for constant disturbance ofd(t)=[0.01 0.01]T. The trajectory tracking by rigid revolute joint robot manipulator system here does not belong to any of the cases mentioned in Remark 2. There does not exist any zero dynamics for the system considered. The desired trajectory tracking in terms of joints’ angular positions and velocities have been shown in Figs. 1 and 2 respectively. The tracking in these figures are robust even in the presence of uncertainty using the proposed approach. Figs. 3 and 4 demonstrate tracking error of angular positions and velocities of both joints respectively. Both tracking errors show convergence and ensure asymptotic stability of the system. The eventtriggered approach binds chattering in a band as shown in tracking error plots. The event-based sliding mode control input for both joints have been shown in Fig. 5. The control inputs demonstrate aperiodic triggering after 6 s. They are not updated periodically and remain constant for many inter-event intervals. Fig. 6 shows the sliding surface of both joints. Although Fig. 6 illustrates chattering on sliding surfaces, the control law brings trajectory to sliding manifold and ensures system stability. Fig. 7 presents event-trigger error ‖e‖ and trajectory tracking errorBoth the errors converge almost to zero after 6.4 s. The time required for convergence while periodic-triggering is found to be approximately 6 s. The proposed approach takes a little more time for convergence as compared to periodic triggering but the difference is very small. It can be inferred from Figs. 7 and 8 that update of control law occurs only when the conditions (22a) and (22b) are violated. Fig. 7 has been enlarged in Fig. 8 for clarity in presenting all the error parameters with triggering instants after 6.4 s. It shows that aperiodic updates of control actions significantly reduce for desired tracking. These results ensure resource optimization along with stability of system. The value of Lyapunov functionhas been shown in Fig. 9.The number of control updates using the proposed approach are found to be 441 for the simulated duration of 10 s (i.e.,1000 sampling instants). The average frequency of control updates is approximately 44 Hz. Similarly the number of control updates for time varying disturbanced(t) = [0.5sin(3.14t)0.5sin(3.14t)]Tare found to be 606 for the simulated duration of 10 s (i.e. 1000 sampling instants). The average frequency of control updates is approximately 61 Hz. The angular positions and tracking errors of joints for second set of results have been shown in Figs. 10 and 11 respectively. The normalized values of various error parameters have been shown in Fig. 12 with its zoomed view in Fig. 13 along with the triggering instants. A comparison of time-triggered and proposed SMC controller has been done in Table I based on number of events and convergence time of errors. Using (47), the lower bound on inter-event times are found to be 0.0037 s and 0.0032 s for constant and time-varying disturbances respectively. The admissibility in both the cases are maintained as minimum inter-event time is 0.01 s.

Disturbance Approach Samples Convergence time (s)Constant Time-triggered [19] 1000 6.0 Proposed 441 6.4 #Time-varying Time-triggered [19] 1000 6.2 Proposed 606 6.7 #

V. CONCLUSIONS

The work in this paper presented the event-driven sliding mode control for tracking problem of a class of nonlinear input affine system in the presence of the uncertainty. The proposed approach guarantees asymptotic stability for the desired trajectory. It also ensures boundedness of error and avoids Zeno behavior on the sliding surfaces. Inter-execution time for proposed control approach is verified through simulation results. The presented work shows performance of the system at par with traditional periodic triggering approach in the terms of processing time. The proposed approach also significantly reduces the number of actuator actions required to address trajectory tracking problem. This ensures optimization of resources available for any system operation.The approach can be restrictive to some critical applications where high threshold error and chattering cannot be tolerated.This approach can be extended to multi-agent systems in the presence of disturbance and can be implemented on real-time framework in future.