cetol6σ公差仿真分析软件在家用空调结构设计及工艺设计中的研究应用

张先令

ZHANG Xianling

珠海格力电器股份有限公司 广东珠海 519070

Zhuhai Gree Electric Co., Ltd. Zhuhai 519070

1 引言

随着市场需求、质量控制、成本控制等方面需求的变化，新产品开发对于外观间隙台阶、性能等要求越来越高。然而，新产品开发过程中，从结构设计到结构审查，各单位对于尺寸链计算的重视程度远远不够，缺乏专业的尺寸链计算，设计及审查人员更多的还是依据经验及试错的手段去验证，很多问题只能在产品试制阶段发现，导致产品投模后频繁更改。

一般情况下采用excel表格手工计算尺寸链，结果为极值状态，而实际制造不太可能出现所有影响因素都处于最坏情况，按极值计算要求进行控制的话，虽然可以实现零件的完全互换性，保证产品质量100%合格，但是也存在一定程度的质量过剩造成的成本浪费；并且，对于包含形状公差、位置公差等在内三维空间复杂尺寸链的计算，手工计算显得非常困难且容易出错。因此，三维公差仿真分析软件应运而生。

三维公差分析软件，能够模拟实际零件公差分布以及随机取样组装情况进行仿真分析，以实际产品装配约束关系模拟仿真分析，支持建立封闭尺寸链，分析组成环公差对封闭环公差的影响，预测封闭环尺寸的统计分布图和极限分布图。及时发现未知问题，并进行相应的结构设计或工艺设计优化，避免以往凭经验“试错法”导致的资源浪费、成本高、开发周期长等问题。并输出敏感度、贡献度排序表，以便分析人员快速找到问题症结，并针对性的制定改进方案进行模拟仿真验证；还可以提炼关键装配工序、关键零件、关键公差等控制要素，以便对重点制造过程进行控制。

2 公差分析方法

公差分析是根据产品装配关系、综合设计尺寸、装配偏差、零件加工误差等因素，计算产品分析目标累计公差的过程。计算结果如达不到设计要求，需优化结构设计方案或调整零件公差等因素再重新计算。公差分析主要包括极值法和统计法两类。

2.1 极值法分析

即最坏情况分析。实现最坏情况分析，要求所有的尺寸都处于最大偏差尺寸值。公式如下：

极值法举例：50（±0.1）+50（±0.1）=100（±0.2）。

在目前的公差分析理论中，极值公差法虽然计算量小、理论简单。但由于所有零件的公差同时处于极值情况的可能性很小，因此该理论通常对零件尺寸公差、零件装配精度等要求过高，常常导致产品成本偏高。

2.2 统计法

统计分析方法，目前行业应用较广的包括VSA、3DCS、cetol6σ等软件，本文基于cetol6σ公差仿真软件进行阐述。统计分析方法是根据产品实际装配关系建立约束条件，模拟实际零件公差分布、随机取样组装情况，表达具体尺寸公差、装配关系等因素对产品质量的影响。

统计法利用样本的算术平均值和标准偏差确定一个标准正态分布曲线。标准偏差可以由一系列的分布要素计算：

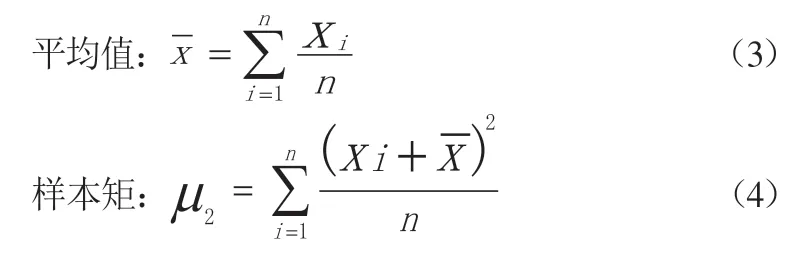
次样本矩：

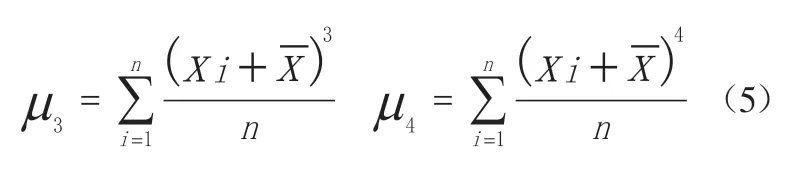
式中：Xi为样本空间中的元素；n是样本的维数；可以预先给定μ2、μ3和μ4，然后再计算出一系列的其他要素：

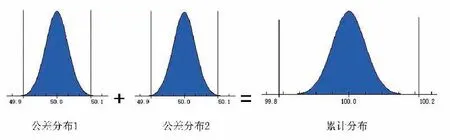
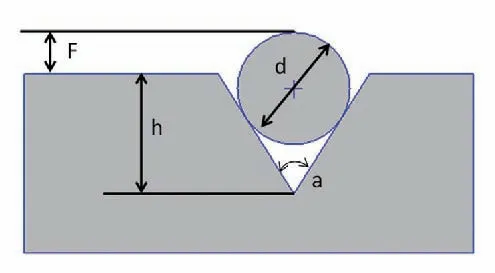
图2敏感度示意图

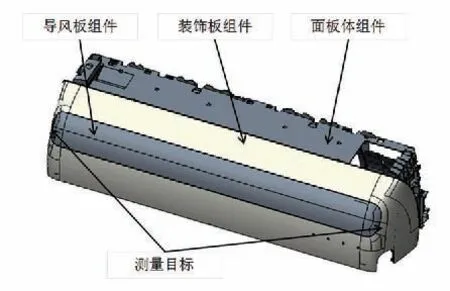
图3空调出风机构示意图

样本标准方差的计算公式为：

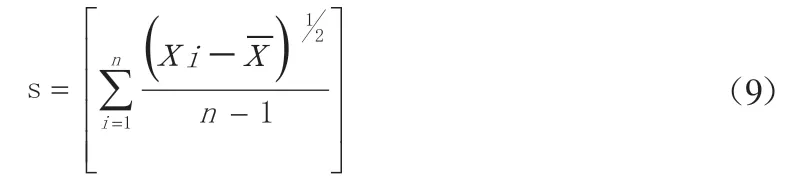
由均值、标准偏差、斜度和峰值定义的分布一般称为Lambda分布，是一般情况下的统计分布。统计法举例见图1。

2.3 结果数据分析

2.3.1 贡献度计算方法

图4统计分布公差仿真分析结果

图5调整分布中心后的统计分布示意图

图6贡献度排序表

贡献度是描述装配尺寸链中各个组成环尺寸公差对封闭环尺寸积累公差的贡献大小。采用百分比的计算方法，分为最坏情况下的百分比贡献度和统计情况下的百分比贡献度。

最坏情况计算公式为：

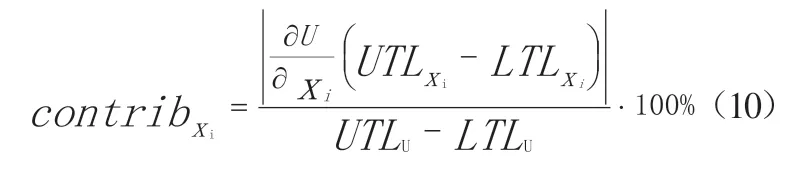
其中：UTLxi是xi的公差上限，LTLxi是xi的公差下限；UTLU是U的公差上限，LTLU是U的公差下限。

统计情况计算公式为：

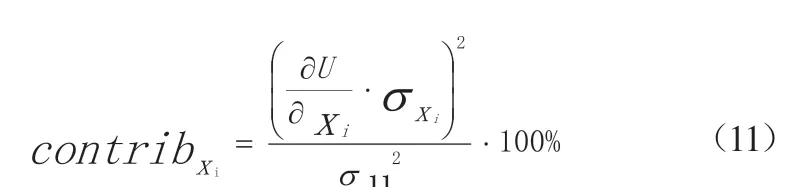
其中：xi为模型中第i个零件尺寸，U为设计尺寸，σxi为xi的标准偏差，σU为U的标准偏差。

通过贡献度计算并排序，可以直观看出尺寸链各组成环对分析目标的影响程度，针对影响程度高的组成环，我们可以定义为关键因素，再生成制造过程进行重点监控控制，甚至可以通过提高关键因素的加工精度等方式，达到提高产品性能指标的需求。

2.3.2 敏感度计算方法

当在cetol定义好了各个部件的配合关系，就会自动建立闭环尺寸对组成环尺寸的函数关系式，如图2的F为封闭环尺寸，其余尺寸如圆柱直径d、楔块高度h和楔块角度α与F建立的函数关系式为：

通过求封闭环尺寸对组成环尺寸的一阶偏导数：

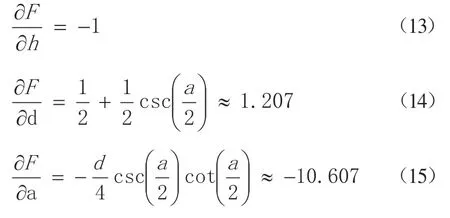
从而得到h相对于F的敏感度数值为-1，d相对于F的敏感度数值为1.207，而α相对于F的敏感度数值为-10.607。因此三维空间的敏感度计算比较复杂，通常根据装配尺寸链形成的传递函数，求封闭环尺寸对组成环尺寸的一阶偏导数或二阶偏导数。

人力资源管理人员要根据组织和员工特性，有规划地引导开发和调任，满足岗位设置的基本要求，结合人才的特点，分析周围的工作环境，合理规划岗位，激发人才的内部潜能，鼓励他们就参与企业决策中来，提升信息的对称性和人才的主人翁意识，满足当前企业发展的基本要求。

从三维产品开发的角度，根据敏感度计算公式，可以计算各种尺寸的敏感度，这样可以清楚地知道在同一时间更改设计尺寸值时，比较各个数值的重要程度，有针对性地更改与品质相关联的设计尺寸，这就意味着高敏感度的尺寸，会对设计结果产生直接影响，通过控制高敏感度的尺寸来尽量减少质量产生的波动，从而有效地控制整个产品的质量。

3 案例仿真

以某家用分体壁挂空调内机新产品导风板两端配合外观面差问题进行仿真分析。

3.1 分析目标

如图3所示，分析分体内机导风板两端与装饰板长度方向配合面差问题，根据工业设计及市场调研评估，认为面差控制在±1mm以内比较美观。因此，在cetol分析界面中，设置分析目标尺寸为：0f 1mm。

从尺寸链关系分析，外导风板与内导风板通过胶粘贴成一个组件，然后一起装配到面板体组件的左右驱动盒上，而左右驱动盒固定在面板体上；同时，装饰板与基板也胶粘成一个组件，一起装配到面板体上。总体尺寸链关系：外导风板-内导风板-左驱动盒组件-右驱动盒组件-面板体-基板-装饰板，最后回到外导风板，总共涉及6个零部件。

3.2 产品装配建模

在整个装配体中，以面板体为基础，首先将左右驱动盒组件装到面板体上，然后装配装饰板组件，最后装导风板组件。

装配约束总体遵循产品实际装配原则，通过限制零件的6个自由度，确定零件的装配约束建模，约束特征包括面/线/点、轴/孔等，约束关系包括面接触、线接触、点接触、同轴、与点同心等，具体根据实际装配结构情况而定。

3.3 定义零件公差

新产品方案设计与方案审查阶段仿真分析时，尺寸公差一般基于国标或企业内部标准来定义；产品试产后的公差仿真一般基于受控工程图纸及实际零件制造能力水平来定义尺寸公差。

4 仿真结果分析

4.1 结果分析

建立装配约束并定义零件公差后，即可使用cetol软件运行求解，并生成分析报告。分析结果如图4。从统计分析结果来看，合格率仅为86.6%，合格率太低，无法满足生产质量要求。其中，图4中红色区域为超出±1mm台阶要求的概率；并且，从统计分布图可以看出，分布中心偏移远离合格范围中心，需要进行优化。

4.2 公差分析优化

首先，需要解决分布中心偏移问题，从分析结果看，分布中心在-0.43mm位置，此类问题一般考虑从以下三个方面改善：（1）考虑优化设计结构，尽量让设计值与合格范围中心趋于一致，提高合格率，本案进一步分析属于导风板长度定位偏移导致分布中心偏移，调整结构后分布如图5所示；（2）基于原始设计台阶考虑，采用偏移公差，使得统计分布中心与合格范围中心趋于一致，提高合格率；（3）以上两种措施都无法有效解决时，可重新审视合格范围制定是否合理，评估是否可以根据统计分布情况进行适当调整，以提高合格率。

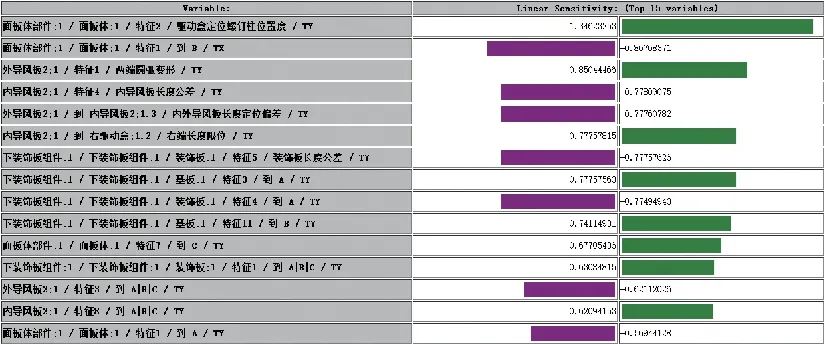
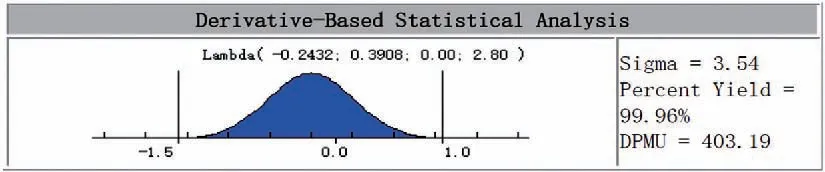
图8公差分析优化结果

（1）提高零件加工精度，缩小公差带范围。可以通过贡献度排序表（图6）、敏感度排序表（图7）提炼关键零件、关键尺寸公差（图8），并评估考虑提高其控制精度，达到提高产品合格率的效果；

（2）提高零件之间配合精度，减小装配误差。同样可以通过贡献度排序表（图6）、敏感度排序表（图7）提炼关键装配控制要点，并评估考虑提高其配合精度，达到提高产品合格率的效果；

（3）针对尺寸链比较长的产品，优先考虑通过结构优化，缩短尺寸链，减少影响因素；

（4）针对尺寸链特别长的产品，可以考虑通过工装夹具等措施，绕过尺寸链，大大减少影响因素。

5 分析总结

通过仿真机理及案例仿真分析，我们认为cetol公差仿真分析软件可以有效用于家用空调产品结构设计与评

审等阶段的公差仿真分析，其主要意义包括：（1）产品方案审查

评估设计产品能否符合关键质量要求，预估合格率，避免产品开发过程中关键外观间隙台阶、关键功能等因尺寸链设计异常导致产品不合格。

（2）设计结构优化

根据分析结果中的敏感度排序表，对产品进行创新设计或改进设计，提供改进方向和改进参考依据。

（3）工艺设计优化

根据分析结果中的敏感度、贡献度排序表，预测影响产品质量的关键零件、关键尺寸和公差，提出合理的控制和优化方向，为关键零件一致性控制、关键工序控制等提供理论依据，提高产品质量的一致性。

（4）公差分配优化

根据仿真分析后的贡献度数值，调整关键尺寸的公差，使得产品的质量大幅度提高；相反，对于贡献度数值小的尺寸公差，可以放大其公差，从而降低各部件的加工成本。

（5）异常问题分析整改

对于涉及尺寸链设计或控制不合理的生产异常问题，使用软件分析，找出异常问题关键原因，并通过优化结构设计或工艺设计改善产品质量，并在软件环境下进行理论分析验证。