测井解释方法探究

张永健，黄海涛，汤子余，金玉堂

（1.长江大学石油工程学院，湖北武汉 430100；2.中油测井新疆分公司测井，新疆克拉玛依 834000；3.中海艾普油气测试有限公司，天津 300300）

测井解释技术在早期，主要是被用于寻找油气藏。从20 世纪末期开始，有了更大的发展，它可以更好的勘测地层的地球物理性质[1]。在与地质研究结合起来后，测井解释技术还具有辨别裂缝以及解释岩石的机械性质等特殊用途，是现代油气勘探开发中必不可少的重要技术之一[2，3]。从2004 年刘传平、杨青山等建议应用岩石物理相分析技术以及水淹层测井响应信息的研究方法来解释薄差层水淹层[4]。到2015 年黄薇、张小莉等加入有机碳含量来完成鄂尔多斯盆地中南部延长组7段测井解释模型的建立[5]。随着石油勘探开发技术研究深度的不断提高，各种测井解释技术也在不断的优化和加深。

1 测井资料预处理

1.1 岩心深度归位

在油藏的勘探开发中，岩心分析数据能较为真实地反映地层岩性及储层物性等特征，但由于人为操作或仪器本身误差，导致钻井取心的岩心深度和测井深度不一致，为了增加岩心分析数据的准确性及后期测井参数模型的精度，需要对岩心深度进行校正处理。岩心归位处理的常用方法有两种：一是对比岩心的泥质含量和自然伽马曲线，来完成深度的校正；另一种是通过三孔隙度曲线与岩心实验所得的孔隙度进行深度校正，完成岩心归位。在岩心归位处理的过程中，应遵循以下原则[6]：（1）将物性、岩性相似的岩心归为一层；（2）层内岩性、物性夹层需加入层内的平均参数计算；（3）每层的样品数应在5 块以上；（4）区域样品异常值不参与计算。

1.2 测井曲线标准化

在油气田的长期勘探开发中，难以确保所有测井数据属于同一类型，具有统一的标准尺度和相同的运行模式，这将不可避免地导致基于井和井之间的比例因子的误差。因此，就有必要标准化测井数据，以提高解释可信度[7]。

测井数据的标准化处理的实质是依据油藏的同一层段，其地球物理特性是相同的[8]。其中受区域构造条件影响，使得标准化方法有所不同，常用的标准化方法有：直方图法、均值方差法和趋势面分析法等。如果区域跨度很大且其空间分布有明显差异，选用趋势面分析法，相反选择用直方图法，均值方差法[9，25]。

选取标准层是进行测井数据标准化必不可少的一步，其选取应遵循如下原则[9，10]：（1）在研究区域内分布很广，厚度通常大于5 m；（2）属于地层响应特征稳定的岩层；（3）岩性、电性响应特征明显，方便全区追踪对比。其中，标准层的特征值通常是层的平均值，也可以通过使用对数数据直方图或频率图来选择特征值。

2 测井参数解释模型

在测井解释的过程中，完成了测井资料的预处理后，接下来就是建立各种测井参数的数学模型，为了使建立的测井参数解释模型更为准确，必须考虑各类影响参数。同时，还要充分利用岩心实验数据，以使模型精度更高。创建高精确度的测井参数解释模型是油藏后期开发工作的前提，只有这样才能更精细的研究储层[11，12]。

2.1 泥质含量模型

泥质是各类黏土矿物、细粉砂和其他非黏土矿物构成的一种混合物，并且都受到各类因素影响而不能直接测量[13]。由于泥质的测井响应的存在，将会导致解释的测井参数不准确，因此，在测井解释的过程中必须进行泥质校正。

在砂岩地层中，由于泥岩中含有黏土和软泥等放射性物质，其自然伽马值会偏大，而其他岩层放射性物质含量极低，其自然伽马曲线会呈现出低值。故常用自然伽马来计算泥质含量，在没有伽马测井曲线时，可以通过自然电位曲线或者其他测井响应明显的曲线来替代。其计算公式[14]为：

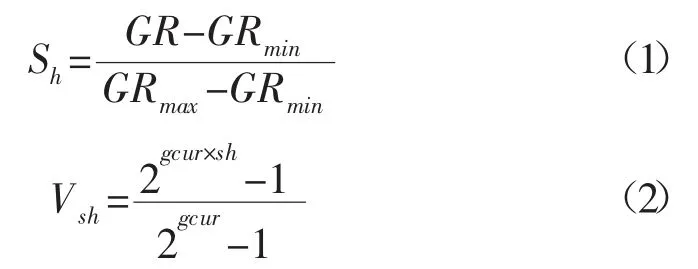
式中：GR-自然伽马测井曲线响应值；GRmin、GRmax-统计井段中自然伽马的最小值和最大值；Sh-自然伽马曲线的相对值（无量纲值）；gcur-经验系数（新地层一般取3.7～4，老地层一般取2）；Vsh-地层泥质含量。

在砾岩储层中，由于砾岩是快速混合和聚集的结果，其中含油较多的岩屑和长石，由于受到其中放射性矿物的影响，自然伽马曲线反映储层泥质含量的准确度会降低。因此，在砾岩储层中，泥质含量的计算不能选择自然伽马或自然电位曲线，通常选择密度和中子测井曲线[15]。这是因为它们测井原理不同，中子和密度测井采用的是核测井原理，其受到岩性及非均质性的影响更低，能更明显的反映出泥质含量的多少。

2.2 孔隙度模型

通常地质学者在研究地层储集能力时，将孔隙度作为主要研究参数之一。在储层孔隙中，当其饱含流体时，运用孔隙度测井系列均能取得较好的效果。常见的计算方法有以下两种。

2.2.1 体积模型法 假定因变量为岩心实验所得孔隙度，自变量为测井所得数据，经过岩性相关性分析取得岩石骨架值，其中主要影响值有中子、密度和声波，孔隙度模型如下[16，25]：

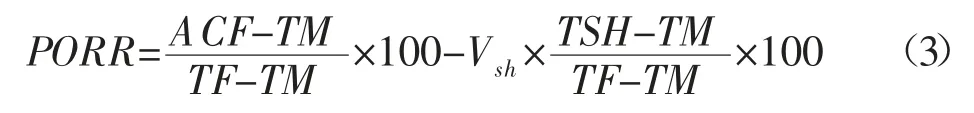
式中：PORR-地层有效孔隙度，%；ACF-校正后的声波时差值，μs/m；TSH-解释层段内泥岩声波时差值，μs/m；TF-流体声波时差值，μs/m；TM-砂岩声波骨架值，μs/m；Vsh-所在深度点的泥质含量，%。

2.2.2 回归拟合法 孔隙度主要受到岩性因素及孔隙结构影响。前人通过分析大量取心资料和测井数据，表明岩心分析资料与声波测井之间的相关性很好[17]。因此在不考虑泥质含量的情况下，通过声波测井和孔隙度回归可以得到以下孔隙度模型：

式中：por-孔隙度，%；AC-声波时差，μs/m；a、b-线性关系式相关系数。

在考虑泥质含量的影响情况下，可以通过声波、孔隙度和泥质含量建立多元回归公式：

式中：φ-有效孔隙度，%；AC-声波时差，μs/m；Vsh-泥质含量，%；a、b、c-线性关系式相关系数。

当一些井没有声波时差数据时，可通过对已求得孔隙度的部分井的孔隙度与其他测井曲线作相关性分析，得到之间关系性，从而求取缺失声波时差数据的这些井的孔隙度。

2.3 渗透率模型

渗透率是反映油气藏渗流能力的主要参数之一，是决定油气藏是否具备商业开采价值以及产能大小的重要因素[18，19]。目前在渗透率与储层测井响应之间并没有一个明确的定量关系，大多数情况下，渗透率与孔隙度之间的相关性是最好的。但是储集层微观孔隙结构是非常复杂的[20]，有些区域不一定符合这类关系，应依照实际状况展开研究。如下是经常使用的几种计算方法：

（1）对于均质储层来说，通常选择Timur 公式来计算地层绝对渗透率[21]：

式中：φ-孔隙度，%；Swb-束缚水饱和度，%；a、b-经验系数；K-绝对渗透率，10-3μm2。

（2）用粒度中值、孔隙度来求取渗透率，由于渗透率也受到束缚水饱和度的影响，而束缚水饱和度受粒度中值影响最大，故应先求出粒度中值，在优选岩心资料的前提下，通过回归可以得到粒度中值与泥质含量的关系式[16]：

式中：Md-粒度中值，mm；Vsh-泥质含量，%。

在与孔隙度和粒度中值等进行相关性分析，可建立渗透率解释模型：

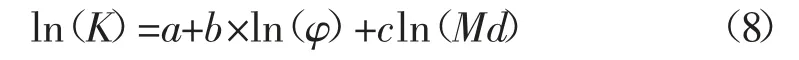
式中：φ-孔隙度，%；Md-粒度中值，mm；a、b、c-回归系数。

（3）对于渗透率的计算，存在多种控制因素，如岩石孔隙、泥质含量等，如若孔渗相关性较好，去掉有裂缝显示、油迹以下及与总体趋势不符合的数据点[22]，则可根据岩心实验数据，得到渗透率的计算模型：

式中：K-渗透率，10-3μm2；φ-孔隙度，%；a、b-回归系数。

2.4 含油饱和度模型

地层含水饱和度是反映储层物性的主要参数之一，是指可动水占的孔隙体积。由于影响因素复杂多样，含水饱和度的计算公式较多，饱和度解释模型大体上可分为以下四类：Archie 公式解释模型、考虑到泥质因素的饱和度解释模型、涉及到骨架及多重孔隙影响的饱和度解释模型和非均质地层中基于网络导电的通用饱和度解释模型[23]。常见的含油饱和度模型有如下三种：

（1）深侧向电阻率的径向探测能力是非常强的，能测到地层的原状电阻率，同时其电阻率数值也受地层水矿化度的影响。因此，在岩心实验的基础上，可以采用深侧向电阻率、有效孔隙度、地层水电阻率作为因变量，来建立含油饱和度模型：

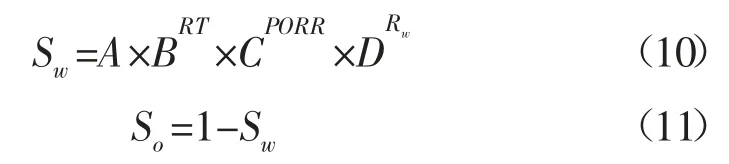
式中：Sw-地层含水饱和度，%；PORR-有效孔隙度，%；RT-地层电阻率，Ω·m；Rw-地层水电阻率，Ω·m；So-地层含油饱和度，%。

（2）在岩心实验的基础上所构建的地区性经验公式相关性很好，但它也过于依赖于岩心实验数据的准确性。建立地层含水饱和度的众多方法中，最经典的是阿尔奇公式，实际应用效果很好。但需要注意的是，在求取岩电参数时，由于岩性不同会导致含水饱和度不同，故需要分岩性来选择岩电参数，其公式表达如下：

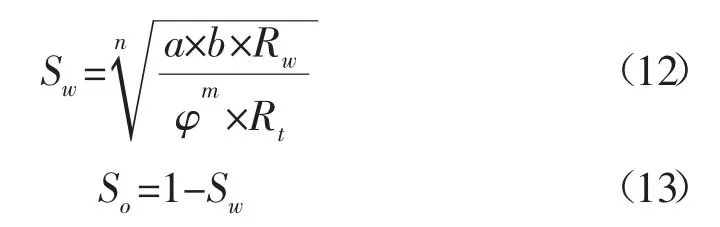
式中：Sw-含水饱和度，%；φ-孔隙度，%；Rt-深侧向电阻率，Ω·m；Rw-地层水电阻率，Ω·m；a-岩性系数；b-与岩性有关的系数；m-胶结指数；n-饱和度指数；So-地层含油饱和度，%。

（3）在建立老区块的饱和度模型时，鉴于该类油田测井系列较老且没有岩电实验，但可得到电阻率测井及泥质含量参数，因此一般选用Simandoux 模型来计算含水饱和度[24]。由于Simandoux 模型中充分考虑了泥质含量以及泥岩电阻率的影响，当储层中泥质因素影响占比较大时，也可选择该模型，其模型为：

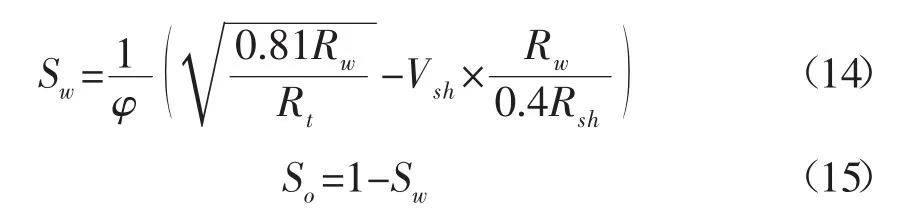
式中：φ-孔隙度，%；Rw-地层水电阻率，Ω·m；Rt-地层电阻率，Ω·m；Rsh-泥岩电阻率，Ω·m；Vsh-泥质含量，%；So-地层含油饱和度，%。

3 模型检验

为了检验建立的解释模型是否正确，需要对创建的参数模型进行验证，常用的检测方法有以下两种：一是用岩心实验所得的孔隙度和渗透率，与用测井解释模型算得的孔隙度、渗透率进行对比，若两者差距合理，则测井参数模型较为准确；另一种方法是通过生产数据对测井参数模型来验证。

4 结论

（1）在测井解释中，岩心归位和测井曲线标准化是第一步，对于后续的参数模型是否准确有极大的影响，岩心及标志层的选取都应遵循各自的选取原则，处理方法则需要依据当地的地质条件来选择。

（2）在测井参数解释模型中，由于含油区域地质状况及测井仪器的不同，其测井参数的计算方法也不同。对于泥质含量而言，由于砂岩和砾岩储层中放射性物质含量的不同，其计算方式也不同；在创建孔隙度模型时，则需依据现场数据来选择计算方法；由于储层测井响应与渗透率之间相关性极其复杂，其计算方式的选取需要考虑储层的非均质性、孔渗关系、束缚水饱和度等因素；由于地层含水饱和度的影响因素复杂多样，其计算方式较多，在建立含油饱和度模型时，需要充分考虑到研究区域的实际情况，如：研究区域是海相还是陆相油田，是老油田还是新油田，是否需要考虑其泥质、骨架、多重孔隙的影响等。