基于采样控制的时滞神经网络的指数同步
(山东科技大学 数学与系统科学学院, 山东 青岛 266590)
神经网络由于其优越的学习、联想记忆及高速寻找优化解的能力,被广泛应用于模式识别、图像处理、自动控制及组合优化等各个工程领域[1-2]。然而,在神经网络的大规模集成电路实现过程中,由于受到运算放大器有限的切换速度的影响,神经元之间的信息传递存在时滞现象。时滞的存在往往会引起系统的振荡,甚至导致系统的发散和不稳定。因此,研究时滞神经网络的动力学具有重要的理论意义与实际价值。另一方面,自Pecora 和 Carroll[3]开创性地提出并在电子电路上实现了两个混沌系统的驱动-响应同步以来,同步控制引起了国内外学者的极大兴趣[4-7],许多有效的控制方法被相继提出,包括状态反馈控制[10]、耦合控制[11]、自适应控制[7]、脉冲控制以及采样控制[13-15]等。
然而,由于受网络带宽的限制,上述传统的点对点控制方式易导致网络发生拥塞和丢包等现象。随着通信技术和计算机技术的发展及其在控制系统中的不断应用,网络化控制方法被提出并得到了广泛的应用[16]。网络化控制是一种将被控对象、传感器、采样器、控制器和执行器通过共享信息网络连接起来进行信息交换的控制方法,它可以有效地降低数据包的传输次数,节省有限的带宽。采样控制是网络化控制的重要手段之一, 可以显著降低数据包的传输频率。目前采样控制的研究方法主要有三种,即离散化方法[13]、脉冲模型法[14]和输入延迟法[15]。输入延迟法由Fridman提出[15],其本质思想为:首先将采样控制系统转化为具有输入延迟的连续系统,然后通过建立一种新的李雅普诺夫泛函,来分析被控系统的稳定性。
事实上,采样控制系统本质上是一类时间依赖的切换系统,传统的时间不依赖的Lyapunov泛函方法不能很好地反映系统的这种切换特性,且得到的同步判据保守性较高。为了克服这一缺点,本研究构造了时间依赖的Lyapunov泛函。为了节约网络资源,降低信号的传输频率,在采样控制框架下,利用时间依赖的Lyapunov泛函来研究驱动-响应时滞神经网络的同步问题。首先,采样控制能够减少计算负担,提高网络资源的有效利用率。与传统的连续性控制相比,它是实现神经网络同步的一种经济有效的手段;其次,本文采用的分析方法是基于具有自由矩阵的Lyapunov泛函和积分不等式放缩技术,其中,构造的Lyapunov泛函是时间依赖的,能够充分利用采样区间上的状态信息。
本研究在输入延迟法的框架下,研究了周期采样控制下驱动-响应时滞神经网络的指数同步问题。结构如下:第一部分,建立驱动-响应系统的数学模型并设计采样控制器;第二部分,通过构造时间依赖的Lyapunov泛函并结合线性矩阵不等式技术建立保证误差系统取得指数同步的充分条件;第三部分,通过数值仿真验证了所设计的采样控制器的有效性及所建立的指数同步判据的正确性。第四部分,总结并展望下一步研究工作。
1 问题的提出
1.1 模型介绍
考虑以下驱动-响应时滞神经网络:

(1)
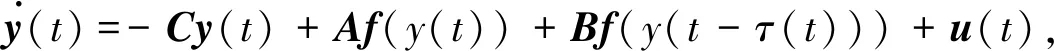
(2)

为了保证驱动-响应系统(1)和(2)解的唯一性,激活函数fj(·)满足如下假设:
假设1.1激活函数fi(x(t)),(i=1,2,…,n)是单调非减的,且满足Lipschitz条件,即存在正常数li,使得对任意的u,v有
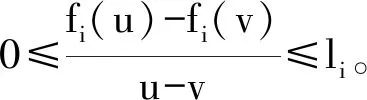
定义系统的同步误差为e(t)=y(t)-x(t),因此得到下面的误差系统:

(3)
其中:g(e(t))=f(y(t))-f(x(t)),g(e(t-τ(t)))=f(y(t-τ(t)))-f(x(t-τ(t)))。
1.2 控制器的设计
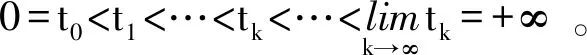
采样控制器u(t)设计为
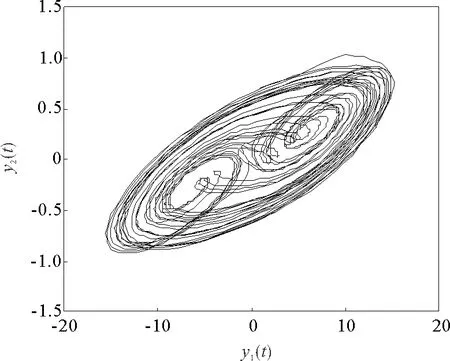
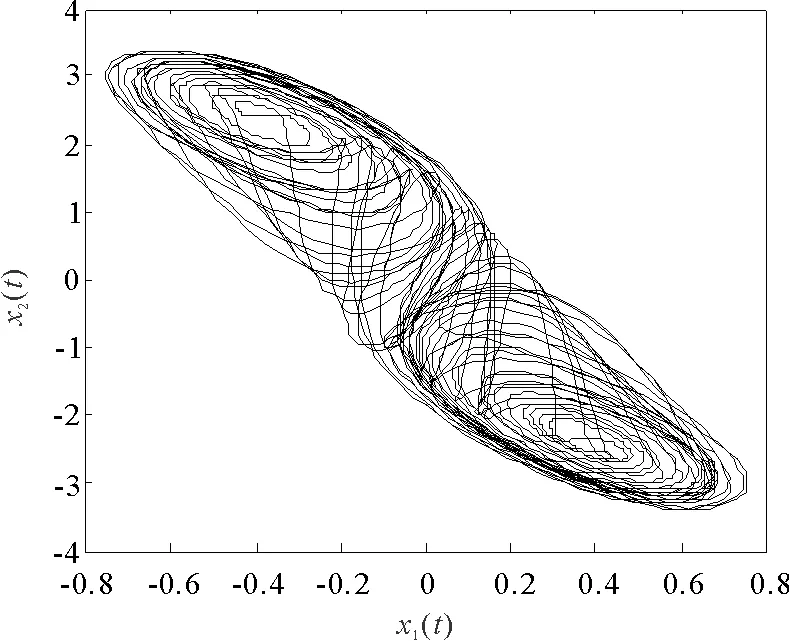
u(t)=-Ke(tk),tk≤t 其中K是待求的反馈控制增益。假设采样周期为h,则h=tk+1-tk。 u(t)=-Ke(t-d(t)),tk≤t (4) 将设计的控制器(4)代入到误差系统(3)中,可得如下闭环系统: (5) 注1:为方便误差系统的稳定性分析,引入虚拟的输入延迟d(t)=t-tk。通过这种手段,可以将离散的误差信号e(tk)转化为连续的误差信号e(t-d(t)),从而形式上将误差系统(3)在采样区间[tk,tk+1)上表示为一个连续系统。 定义1.1[7]称驱动-响应时滞神经网络(1)和(2)是指数同步的,如果存在常数α>0,ϖ≥1,使得 成立,其中φ(s)=(φ1(s),φ2(s),…,φn(s))T和φ(s)=(φ1(s),φ2(s),…,φn(s))T分别是驱动系统和响应系统的初始条件。 接下来,通过引入时间依赖的李雅普诺夫泛函,并结合自由权矩阵方法,给出保证驱动-响应系统(1)-(2)取得指数同步的判据,同时建立保证驱动-响应系统指数同步的反馈控制器的设计方法。 定理2.1对于给定的正常数h,α,τ,μ和反馈增益矩阵K,如果存在正定矩阵Pi(i=1,2,3),对称矩阵Λ1,Λ2和任意矩阵Qi(i=1,2,3),R1,R2,X,X1,满足下面的LMIs (6) (7) (8) V1(t)=eT(t)P1e(t), 对Vi(t)(i=1,2,3,4)关于t求导得 综上可得 -(1-μ)e-2ατeT(t-τ(t))P2e(t-τ(t)) +[2α(h-d(t))-1] [eT(t)(-X+X1)e(t-d(t)) (9) 同时,根据自由权矩阵方法,存在n×n维矩阵Qi(i=1,2,3),R1,R2使得下面等式成立 (10) (11) 另外,因为函数g(e(t))满足Lipschitz条件,因此,存在对角矩阵L=diag(l1,l2,…,ln)和对角正定矩阵Λ1>0,Λ2>0使得下面的不等式成立 2gT(e(t))Λ1Le(t)-2gT(e(t))Λ1g(e(t))≥0, (12) 2gT(e(t-τ(t)))Λ1Le(t-τ(t))-2gT(e(t-τ(t)))Λ1g(e(t-τ(t)))≥0。 (13) 因此,由表达式(9)~(13)可得 (14) 因此,当t∈[tk,tk+1)时,由(14)可得 而当t=0时,有 进一步有 由上式可得 接下来根据定理2.1来求解使得误差系统(3)取得指数稳定的反馈增益矩阵K的设计。 (15) (16) (17) 注2:本研究得到的同步结果是延迟依赖的,与延迟不依赖的同步结果相比,其保守性低,且在实际工程中可以通过求解LMIs计算出延迟允许的最大值,方便其在实际工程中的应用。 例1考虑具有2个神经元的驱动- 响应神经网络系统(1)和(2),其中 图1 驱动系统的混沌吸引子Fig.1 Chaotic attractor of the drive system 图2 响应系统的混沌吸引子Fig. 2 Chaotic attractor of the response system 图3 误差系统e(t)和采样数据e(tk)的轨迹Fig. 3 The trajectories of the error system and the sampled data 例2考虑具有2个神经元的驱动系统 图4 驱动系统的混沌吸引子Fig. 4 Chaotic attractor of the drive system 图5 响应系统的混沌吸引子Fig. 5 Chaotic attractor of the response system 图6 误差系统e(t)和采样数据e(tk)的轨迹Fig. 6 The trajectories of the error system and sampled data 根据定理2.2可得,驱动系统(1)和响应系统(2)在控制器(4)的作用下达到指数同步。 基于采样控制研究了具有时变时滞的混沌神经网络的同步问题。在输入延迟法的框架下,通过设计采样控制器并引入时间依赖的李雅普诺夫泛函,应用自由权矩阵方法和线性矩阵不等式技术,建立保证驱动-响应系统指数同步的LMI准则,该准则与采样周期和同步速率相关。本文设计的控制器能够在减少信息传输和节省通信资源的同时保持系统同步性能。最后,数值仿真实验验证了所得结果的可行性。另外,本研究结果的保守性表现为:为了方便解耦,在定理2中对两个变量做了相关性的假设,这相当于减少了自由矩阵的个数,因此,可能降低了LMIs可行解的范围。下一步拟通过引入更多的自由矩阵或利用新的不等式技术来降低结果的保守性。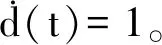
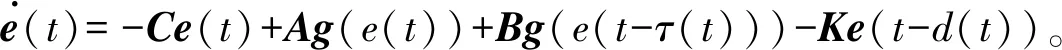
2 指数同步判据
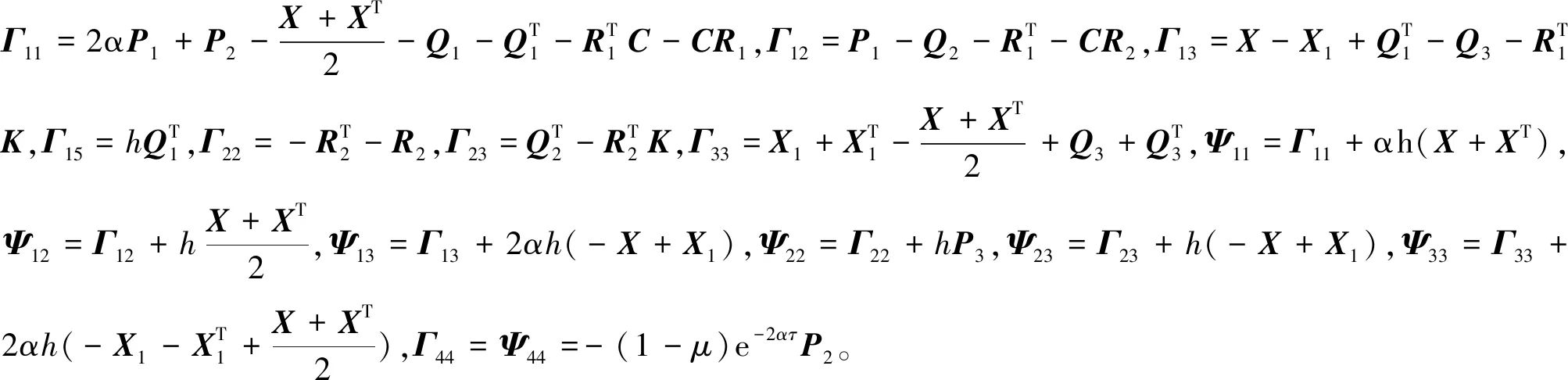
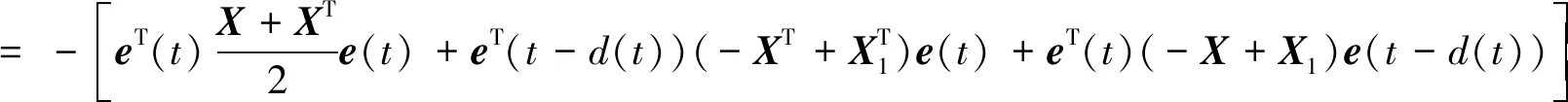
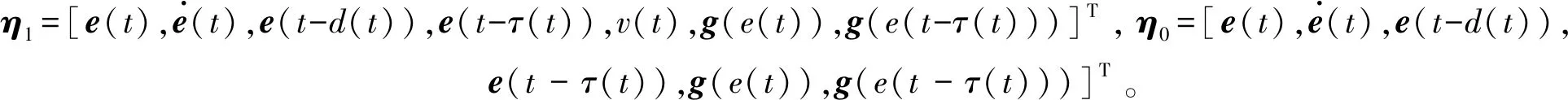
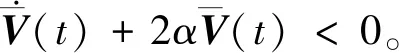
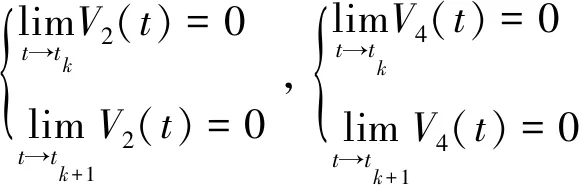
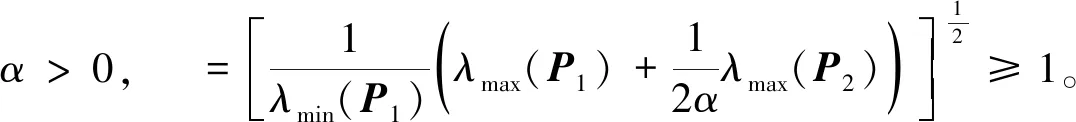

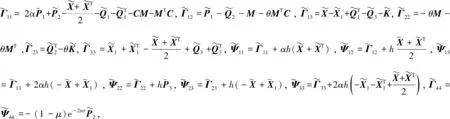
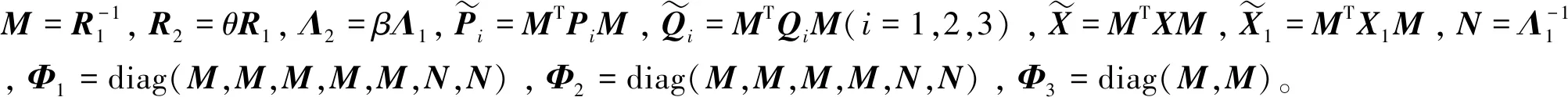
3 仿真算例
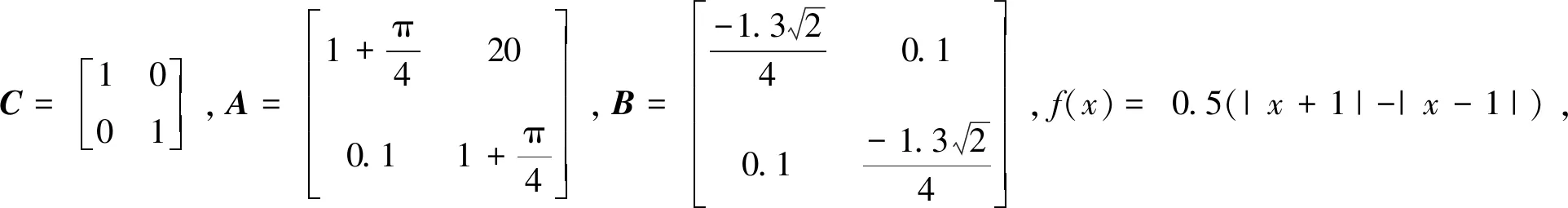






4 结论

