FSP系统建模与仿真分析
刘鸿博,葛攀和,赵守智,胡 古
(中国原子能科学研究院 反应堆工程技术研究部,北京 102413)
空间核反应堆(简称空间堆)具有寿命长、功率密度高、受环境影响小等优点。它在深空探测、星表基地供电等领域均有着广泛的应用前景[1],各国均对其进行过广泛的研究[2-3]。
空间堆系统的瞬态分析在空间堆安全分析和运行控制等方面有着非常重要的作用,因此对空间堆瞬态分析方法的研究具有重要意义。张文文等[4]研究了热管改进型热离子反应堆的瞬态特性,并计算其稳态和瞬态工况下的热工水力特性。袁园等[5]以典型热管堆系统SAIRS为对象,研究了热管冷却空间堆系统从冷态零功率到满功率的启动特性。Radel等[6]利用Simulink对FSP系统进行了建模,并对系统启动、斯特林失效以及冷却剂失去流动的瞬态工况进行了仿真。可看出目前国内的空间堆瞬态分析程序多集中于对热离子堆或热管堆的分析,对于回路式的空间堆的分析研究较少。
FSP(fission surface power)反应堆是美国国家航空航天局(NASA)在经济可承受星体表面裂变反应堆电源系统研究(AFSPSS)项目中提出的反应堆方案[7],目标是作为月球、火星等星体表面的可靠电源。美国已对FSP的设计进行了详细的论证。因此本文以FSP为例,研究对回路式空间堆系统的建模和瞬态分析方法。
1 FSP系统建模
1.1 系统描述
FSP系统结构如图1所示。反应堆使用UO2燃料,堆芯功率为186 kWt。一回路以及中间回路冷却剂均为NaK。冷却剂流出堆芯后通过两个并联的管壳式换热器将热量传递给两个中间回路,之后再通过两个串联的电磁泵回到堆芯入口处。在每个中间回路,冷却剂通过换热器后,经过两组并联的斯特林发电机组的热端。每组斯特林发电机为两台斯特林两两对峙。斯特林发电机的废热通过一个水回路将其传递到热管式辐射器。辐射器热管为钛/水热管。每个辐射器包含两个回路,每个回路所连接的热管互相交错。
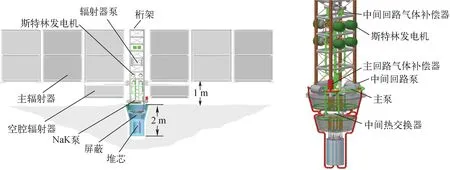
图1 FSP系统概念设计方案Fig.1 Design schematic of FSP system concept
1.2 主要部件建模
1) 堆芯建模
FSP系统堆芯径向截面示意图如图2所示。
堆芯内含有163根燃料棒,燃料富集度为93%,燃料棒包壳为不锈钢。不锈钢筒体厚度为0.25 cm,形状为十二边形。径向反射层为带有不锈钢包壳的Be反射层。反射层上有6个NaK冷却剂的通道,用于对反射层进行冷却。控制鼓所用的材料是带有碳化硼吸收体的Be控制鼓。
堆芯功率采用6群缓发中子的点堆动力学方程进行建模,方程如下:
(1)
(2)
其中:n为裂变功率;ρ为总反应性;β为总有效缓发中子份额;Λ为中子代时间;λi为第i组缓发中子衰变常量;Ci为第i组缓发中子先驱核浓度;βi为第i组缓发中子份额。

图2 FSP系统堆芯径向截面示意图Fig.2 Schematic of FSP system core radial cross section

图3 FSP堆芯径向控制体划分示意图Fig.3 Schematic of FSP’s radial control volume division for core
堆芯热工模型采用单通道模型。燃料棒以及冷却剂的节点划分示意图如图3所示。燃料芯块区域的传热为有内热源的导热,可得沿轴向某层的燃料温度节点方程为:
(3)
其中:j为燃料芯块内部的节点号;ρj(Tj)为节点j的密度;cpj(Tj)为节点j的比定压热容;Tj为节点j的温度;qj为节点j的体积释热率;Aj为节点j的传热周长;λj(Tj)为节点j的热导率;sj为节点j的横截面积;dj为节点j的节点间距。
假设此时燃料和包壳之间未发生接触,那么燃料芯块和包壳之间的间隙利用无内热源导热模型进行建模,可得方程为:
(4)
其中,j为气体间隙的节点编号。
燃料棒包壳基于导热和对流换热模型进行建模,可得方程为:
(5)
其中:j为包壳的节点编号;下标c代表包壳,g代表间隙中的气体;h为包壳和冷却剂之间的对流换热系数;Tf为包壳外部冷却剂节点的温度;Tc为燃料包壳温度。
假设单通道之内的冷却剂不发生横向搅混,因此可得单通道内冷却剂的瞬态方程为:
Ch(Tc-Tf)
(6)
其中:T为冷却剂节点的温度;A为冷却剂流通面积;cp为冷却剂比定压热容;m为冷却剂质量流量;C为燃料棒外部周长。
2) 热交换器建模

图4 换热器管道模型示意图Fig.4 Schematic of heat exchanger pipe
FSP系统采用的热交换器为管壳式换热器,采用类似堆芯单通道模型的方法对其进行简化的建模分析。取单独1根管和其外部流体,假设外部的环形的流体沿着管壁流动,且不与周围流体发生横向搅混,如图4所示。
根据能量守恒,可对管内流体、管壁、管外流体建立如下方程:
πhidi(Ti-Ts)
(7)
hiπdiΔl(Ts-Ti)
(8)
hoπdoΔl(Ts-To)
(9)
其中:下标s、o、i分别为管壳、外部和内部流体;Tif、Tof分别为内部和外部流体的前一个节点的温度;Δl为节点的长度。
3) 热管建模
利用热阻网络法对热管进行建模。在热管完全启动之后相变热阻以及蒸汽流动热阻可忽略[8],又因为绝热段很短,因此轴向传热热阻也可忽略,则简化后的热管模型如图5、6所示。
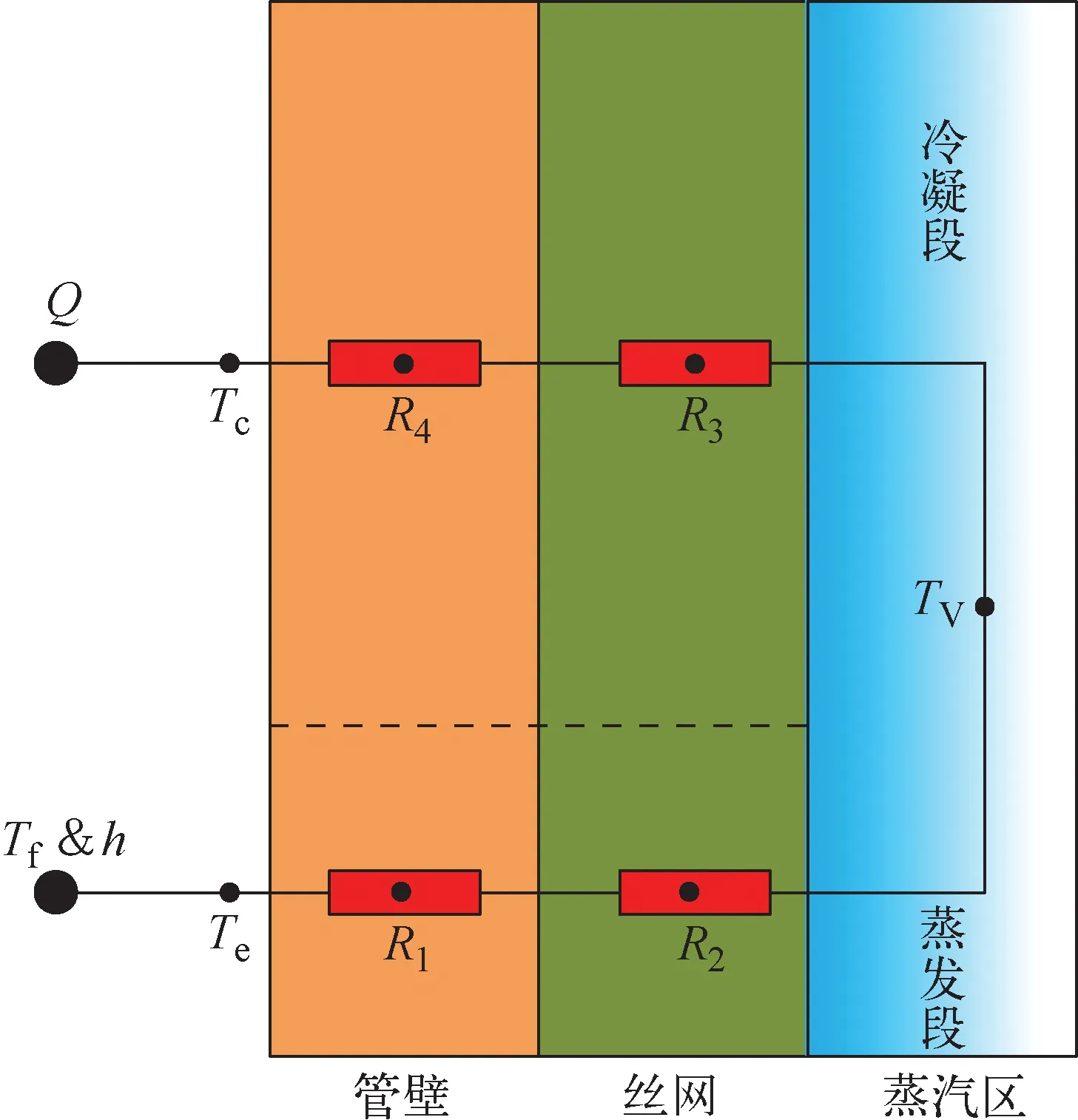
图5 热管热阻网络法Fig.5 Thermodynamic network of heat pipe

图6 一维热阻示意图Fig.6 Schematic of one-dimensional thermal resist
对于1个一维热阻块,有:
(10)
其中:Ti为热阻块中心温度;Ti,1为热阻块左侧温度;Ti,2为热阻块右侧温度;Ri,1和Ri,2分别为左1/2和右1/2的热阻。
热管模型的蒸发段的边界为确定冷却剂温度Tf和对流换热系数h,冷凝段边界为确定辐射功率Q,则可得方程组为:
(11)
(12)
(13)
(14)
其中,s为蒸发段换热面积。
一段圆环管的内外壁面之间的热阻通过如下公式决定:
(15)
其中:d1、d2分别为管外部和内部直径;λ为热导率;l为管长。
4) 回路流量与压力场建模
假设冷却剂为不可压缩流体,那么由动量守恒方程可得:
(16)
其中:Mi为管道内冷却剂质量流量;Ii=Li/Ai,即该单元上的长度除以横截面积;pin为该管道上冷却剂入口压力;pout为该管道上冷却剂出口压力;Δp为该管道上的压力损失,主要包括摩擦压降。在1个回路上,联立各管道上的方程以及节点上的质量守恒方程,则:
(17)
其中:n为某节点分支管的个数;进入节点的dMi/dt设为正、离开节点的dMi/dt设为负。
通过合理设置压力的参考点,可得到一封闭的方程组。求解该方程组,可得到在该回路各管道上的质量流量的导数以及各位置处的压强。
2 FSP系统工况仿真
本文建模与仿真采用Python语言,求解器采用lsoda求解器。仿真输入参数为堆芯功率186 kWt、周围环境温度250 K,一回路泵提供的压头为21 kPa,中间回路泵提供的压头为9 kPa,废热排放回路泵提供的压头为385 kPa。
2.1 稳态工况仿真
通过稳态仿真,将仿真结果和稳态设计值列于表1。可看出稳态仿真的结果和设计值相差很小,结果准确度较高,证明程序能运行到正确的稳态。

表1 系统关键参数仿真结果和稳态设计值Table 1 Simulation result and steady state design value of system key parameter
2.2 反应性引入瞬态工况仿真
正反应性引入会造成反应堆功率升高,在反应堆启动等阶段会出现正反应性引入。考察系统对于正反应性引入工况的响应能更好地理解系统的特点。
通过物理计算得出堆芯总体负反应性系数为-4.4×10-6K-1,并假设其在堆芯功率变化期间无变化,该系数会影响在反应性引入工况下堆芯重新稳定的快慢。
初始状态的堆芯功率为186 kWt,反应堆在稳态的初始状态下引入0.001 Δk/k的正反应性后系统的仿真结果如图7、8所示。
根据计算结果,达到稳态后堆芯功率为232.790 kWt,堆芯入口温度为1 000.83 K,出口温度为1 062.41 K。斯特林冷端入口温度为408.53 K,斯特林冷端出口温度为444.50 K。堆芯功率在上升后逐渐稳定,是由于反应性负反馈的存在,使得引入的正反应性被抵消,从而使堆芯功率重新稳定。堆芯功率的上升造成堆芯冷却剂温度的上升,最终造成辐射器及其相连回路冷却剂温度的上升。可看出的一个特征是冷却剂温度、堆芯功率以及反应性在达到稳定之前均存在振荡。根据图7、8,一回路和中间回路冷却剂温度变化快慢基本一致,但根据斯特林冷端进出口温度变化可看出,废热排放回路中的水温变化明显落后于前两个回路中的冷却剂。设稳态时系统的状态为S0,引入正反应性后系统稳定状态为S1。S1所对应的堆芯功率和冷却剂温度均应高于S0所对应的值。当一回路和中间回路冷却剂的温度上升到它们在S1所对应的温度时,废热排放回路的冷却剂温度还未达到其在S1所对应的温度。之后,随着废热排放回路的冷却剂温度继续升高,造成一回路和中间回路冷却剂以及燃料的温度均超过它们在状态S1对应的温度,因此向堆芯引入了负反应性。从而造成堆芯功率下降,随之引起各回路冷却剂温度的逐渐下降。综上,是反应堆系统各回路之间温度变化快慢不相同,导致在正反应性引入工况中会出现堆芯功率、反应性以及温度的振荡效应。

图7 系统部分温度参数变化Fig.7 Change of some temperature parameters for system

图8 系统部分温度参数、堆芯功率以及反应性变化Fig.8 Change of some temperature parameters, power and reactivity for system
2.3 主泵再启动工况仿真
FSP系统拥有2个主泵,第2个主泵起到冗余备份的作用。当1个主泵损坏后,过一段时间第2个主泵应及时开启。因此,本次仿真针对的即为主泵再启动工况,计算主泵再启动时间间隔为30 s和1 min两种工况,结果如图9、10所示。可看出,辐射器功率在主泵停止后降低,主泵重启后辐射器功率逐渐升高,功率变化趋势合理。而堆芯功率在主泵停止后由于堆芯内热量无法带走,导致堆芯整体温度升高,由于堆芯温度负反馈的存在,会导致堆芯功率降低。图11为主泵停止和重启动工况堆芯反应性。由图11可看出,温度负反馈导致堆芯内产生的负反应性不断加大,且停止时间1 min的工况中最终产生的负反应性要比停止30 s的工况所产生的负反应性大。
同时还可看出,主泵重启后,堆芯功率会产生1个峰。在主泵停止的时间内,废热排放回路由于辐射器的存在而不断降温。当主泵重启时,堆芯功率不断上升,当堆芯功率上升到稳态值时,废热排放回路中的冷却剂温度依然未上升到稳态值,造成一回路冷却剂和燃料温度继续下降。此时堆芯的温度负反馈效应,产生了正的反应性,使得堆芯功率超过稳态的额定功率,但之后功率会逐渐回归稳态。
堆芯内冷却剂平均温度和堆芯出口温度随时间的变化趋势一致。本文的计算结果中,主泵停止时,堆芯内冷却剂温度迅速升高。主泵重新启动时,冷却剂温度迅速降低,这是由于堆芯内高温冷却剂被排出堆芯,之后下降速度变慢是因为堆芯功率不断提高。温度降低到最低后又逐渐稳定到稳态值。冷却剂的温度影响着燃料的平均温度,从而使燃料平均温度和冷却剂温度变化趋势一致。
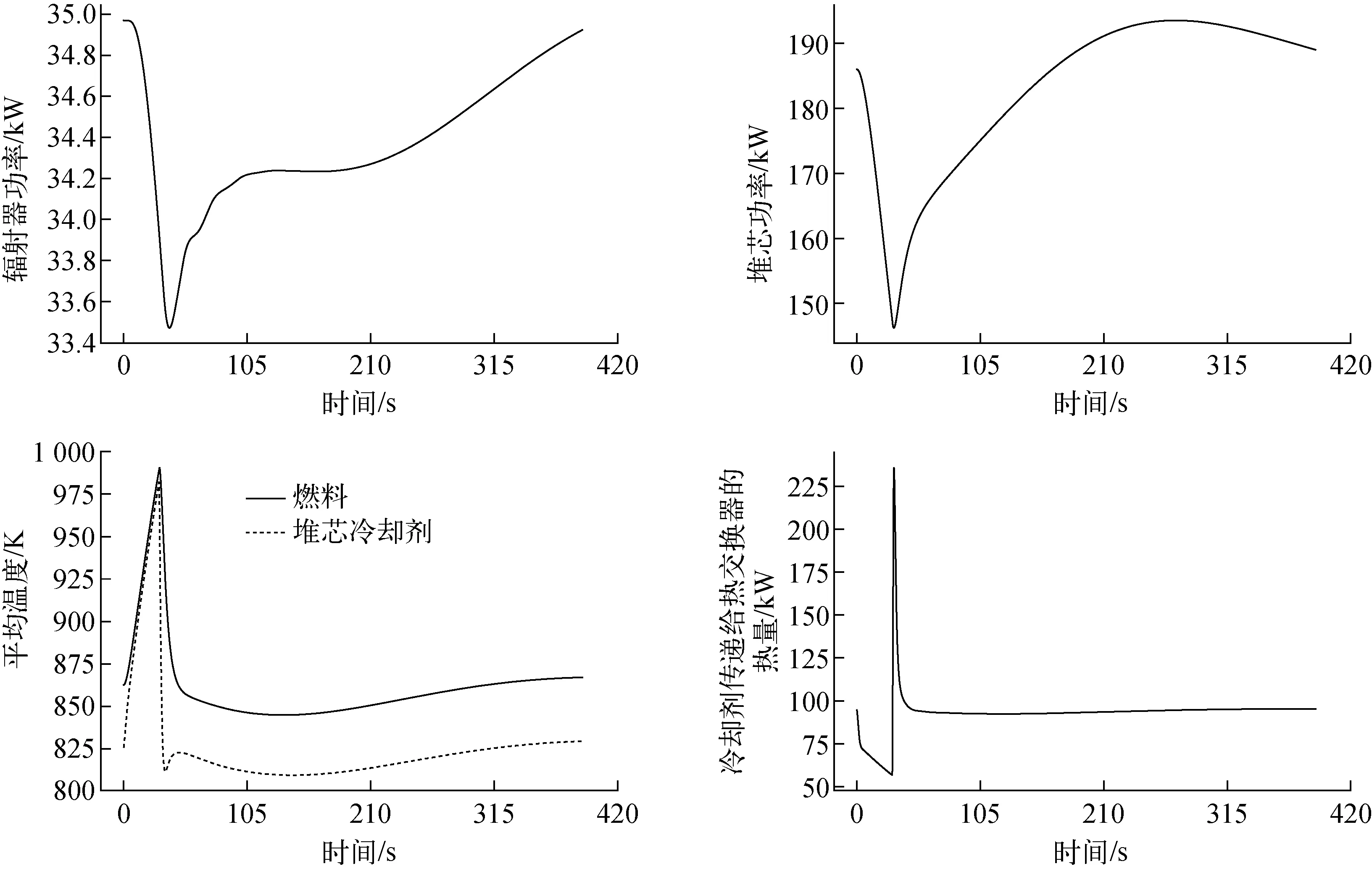
图9 主泵停止后30 s主泵再启动系统响应Fig.9 System response for primary pump stopping at 30 s and restarting
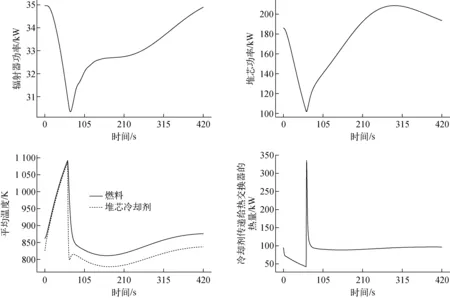
图10 主泵停止后1 min主泵再启动系统响应Fig.10 System response for primary pump stopping at 1 min and restarting
当主泵重新启动时,一回路热交换器管内外流体温差较大,这也是会形成一个功率尖峰的原因。并且可观察到,主泵重新启动的间隔越长,该功率尖峰越大,这种温差可能会对热交换器造成一定的损害,且主泵停止时间过长可能会造成废热排放回路中冷却剂凝固,因此主泵停止后重新启动的间隔越短越好。
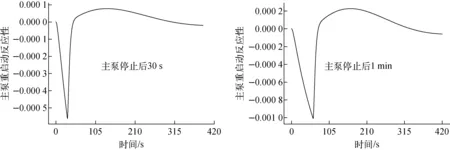
图11 主泵停止和重启动工况堆芯反应性Fig.11 Core reactivities for primary pump stopping and restarting
3 结论
本文通过建立FSP系统分析模型,对该反应堆系统进行了稳态和瞬态的分析计算。稳态的计算结果和设计值相差很小。瞬态计算包括反应性引入工况和主泵停止后再启动工况的仿真计算,计算结果趋势比较合理,说明本文使用的数学模型可较好地仿真FSP系统的瞬态响应。同样在本文中使用的建模方法和思想也可运用于和FSP系统结构类似的反应堆系统中。

