基于FR-Sdaso的法国凤凰堆寿期末自然循环实验分析

齐少璞，杨红义，杨晓燕，王晓坤，王 晋，叶尚尚

(中国原子能科学研究院 反应堆工程技术研究部，北京 102413)

近年来，钠冷快堆作为第四代核能系统中实堆经验最多的堆型受到了越来越多的关注。为证明钠冷快堆的安全性，美国的EBR-Ⅱ[1]和法国的凤凰堆[2-3]均开展过瞬态实验，这些实验既加深了人们对钠冷快堆的了解，同时也为钠冷快堆分析程序提供了很好的分析和验证数据[4-10]。利用系统分析程序开展钠冷快堆的安全分析也是一项重要的研究与设计工作[11-14]。目前我国正在开展600 MW示范快堆的设计与建造工作，为完成其安全分析，开发了系统瞬态分析程序FR-Sdaso[15]。本文以FR-Sdaso为分析工具，对法国凤凰堆寿期末自然循环实验开展建模与分析。

1 凤凰堆寿期末自然循环实验介绍[2]

法国凤凰堆是一座于1973—2009年期间运行的池式钠冷快堆，其热功率为560 MW，电功率为250 MW。法国原子能署(CEA)在其停运之前开展过自然循环实验(部分文献将实验名称由自然循环改为自然对流，但仍为同一实验，本文沿用最初文献的实验名称)[2]，在IAEA[3]的组织下，有8家研究机构针对实验结果开展了计算分析。

凤凰堆采用钠-钠-水的三回路方案，每个回路分为3个环路，整个反应堆共设置了3台一回路钠泵、6台中间热交换器(IHX)、3个中间钠回路、3个水/蒸汽回路。1993年凤凰堆停运了1个环路，只有4台中间热交换器和2个中间钠回路投入运行，并将反应堆热功率降至350 MW(电功率降至140 MW)。在2009年自然循环实验开始之前，反应堆热功率先降至120 MW并维持了4 h，待系统参数稳定后开展了瞬态实验。图1为凤凰堆一回路示意图，包含了主要设备、主要流道和测点位置的示意图，表1为实验开始前的反应堆主要参数，表2为实验过程的主要瞬态节点。

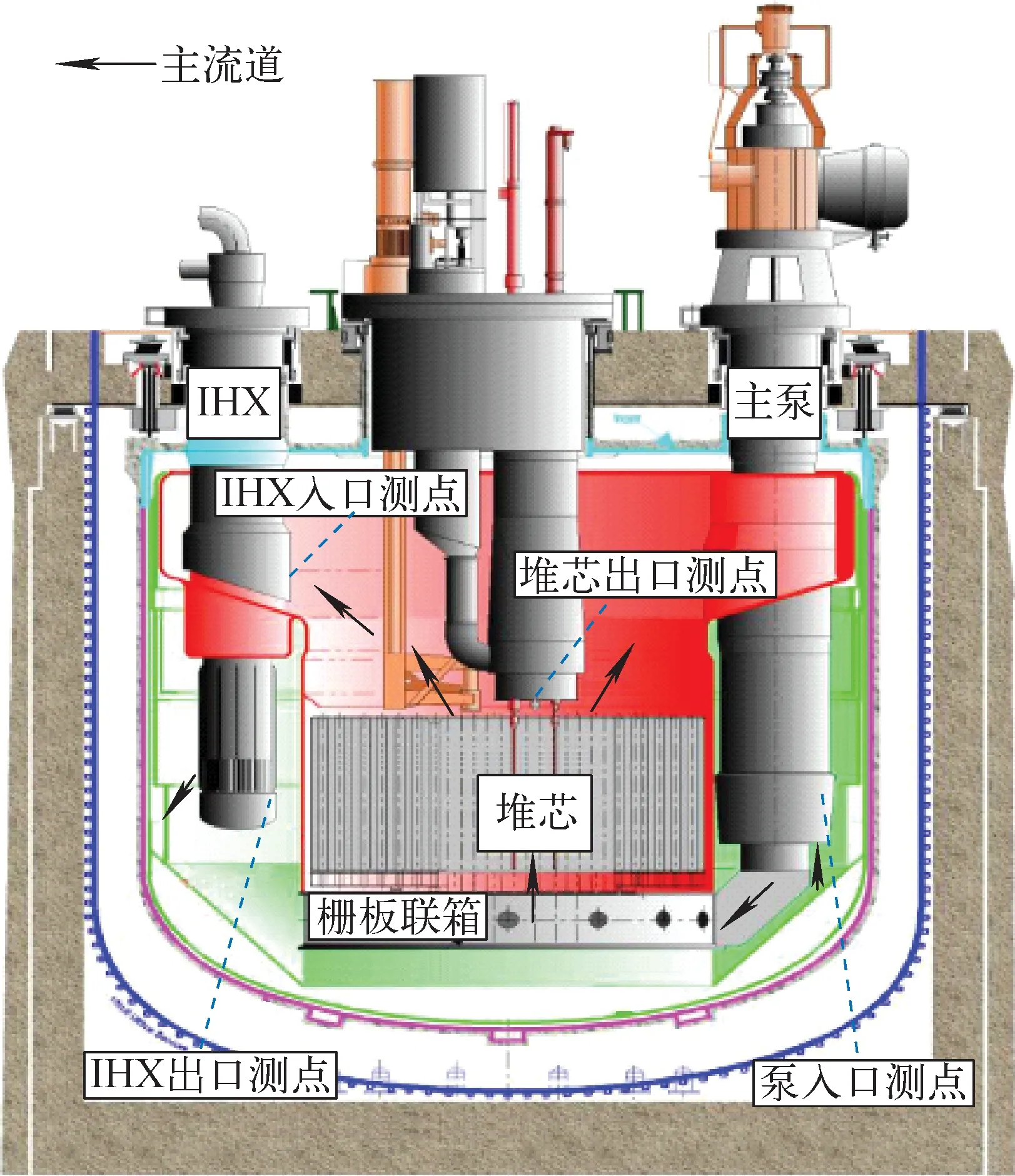
图1 凤凰堆一回路示意图Fig.1 Phenix primary system schematic

表1 自然循环实验前的凤凰堆初始参数[2]
Table 1 Initial parameter of Phenixbefore natural circulation test[2]

主要参数数值堆芯热功率,MW120堆芯流量,kg/s1 284堆芯入口温度,℃358堆芯出口温度,℃432中间热交换器一次侧入/出口温度,℃432/360中间热交换器一次侧流量,kg/s321中间热交换器二次侧入/出口温度,℃308/432中间热交换器二次侧流量,kg/s190一/二回路泵转速,r/min350/390

表2 凤凰堆自然循环实验主要动作[2]Table 2 Main action of Phenix natural circulation test[2]

实验开始时(参考时间t=0 s)，2台蒸汽发生器发生蒸干，整个反应堆进入失热阱瞬态过程(阶段1)，IHX二次侧入口温度逐渐升高，IHX一次侧和二次侧温差开始逐渐减小。458 s后，当IHX一次侧和二次侧温差小于15 ℃时，操作员手动紧急停堆，2台二回路泵转速在1 min内降至110 r/min。停堆8 s后，3台一回路泵停运，转速逐渐惰转至0 r/min(约610 s时)，一回路由强迫循环转为自然循环，实验进入第1阶段自然循环过程(阶段2)，此过程中二回路除散热外无其他热阱。10 320 s后，蒸汽发生器套筒上下两端的风门打开，蒸汽发生器得以通过套筒内空气的自然循环进行冷却，二回路建立了有效热阱，冷端温度稍有滞后便明显降低，实验进入第2阶段自然循环过程(阶段3)。24 000 s时，蒸汽发生器套筒风门关闭，实验结束。阶段1持续约7 min，阶段2持续约3 h，阶段3持续约4 h。

2 FR-Sdaso模型简介与建模

2.1 FR-Sdaso简介

本文采用中国原子能科学研究院自主研发的钠冷快堆系统分析程序FR-Sdaso[15]开展分析。该程序可针对堆芯、主热传输系统及余热排出系统进行建模，能开展稳态及主热传输系统无破口瞬态的分析。其中，中子学模块采用点堆模型，堆芯热工模块采用单通道模型，一、二回路流动换热采用一维模型。此实验[2]将反应堆功率、一回路泵转速、二回路流量、IHX二次侧入口温度作为边界条件给出，本文仅给出本次分析中主要涉及模块的模型简介。

1) 堆芯热工模型

堆芯热工模块采用多管单通道模型，其控制方程如下：

(1)

其中：A为流道截面积，m2；ρ为密度，kg/m3；w为质量流量，kg/s；cp为比热，J/(kg·K)；T为温度，℃；t为时间，s；z为轴向高度，m；qcd为包壳与流体换热项，W/m3；qz为轴向导热项，W/m3；qe为其他换热项，W/m3。

燃料棒采用有限容积法进行导热方程的求解，燃料中心孔处为绝热，芯包间隙以等效热阻模拟，包壳外壁与流体之间为对流换热，燃料棒导热的控制方程如下：

(2)

其中：r为径向距离，m；k为燃料热导率，W/(m·K)；qv为燃料体积释热率，W/m3。

堆芯热工模块沿流动方向求解轴向各层节点温度，流体部分采用一阶迎风格式，燃料棒采用追赶法求解本层径向温度分布。图2为轴向和径向控制体划分示意图。

2) 一回路流动模型

采用特征线方法对一回路主流道和辅助流道构成的流网进行求解：

(3)

图2 堆芯通道轴向(a)和径向(b)控制体示意图Fig.2 Schematic of axial (a) and radial (b) meshing of core channel

(4)

其中：dx/dt=±a为网格和时间步长需满足的关系式；x为流动扰动传播距离，m；a为压力波波速，m/s；p为压力，Pa；g为重力加速度，m/s2；sinα为管道水力坡度；f为摩擦阻力系数；De为水力直径，m。方程针对堆芯和IHX等可视为管道的流道进行求解，考虑了流道间密度及高度差带来的驱动力，可模拟泵停运后的自然循环过程。泵和钠池等非流道设备处理成压力和流量的函数关系式，以设备节点形式出现，不同设备节点可反映自身的特征参数，如钠池可模拟因装量或密度变化导致的液位变化。流道和设备节点一起构成了被模拟的流网。

对于流网管道节点，对方程(3)、(4)进行积分，可得如下差分格式：

(5)

其中，下标P、A、B分别代表当前、上游及下游节点，积分过程中以wA和wB作w积分的近似中值。采用特征线方法求解流网问题时，其时间和空间步长划分较小且满足上述特征线方程，各节点的流动参数变化在1个时间步长内只能影响上下游相邻节点，如此在每个时层进行显式求解即可得到下一时层的流网参数。

3) 一回路换热模型

一回路换热模块主要包含钠池换热与IHX热工两部分。钠池换热模块主要是为了获取钠池的平均温度，采用点模型或分区点模型。

(6)

其中：Mi为控制体质量，kg；φ为控制体热源，W；i为第i个计算控制体或钠池；j为第i个控制体的第j个入口；Ni为第i个控制体的入口控制体总数。分区点模型可考虑钠池不同区域的流体换热，可模拟热分层效应的模型仍在开发之中。式(7)给出了数值离散格式，沿流动方向依次求解本时层内钠池各控制体温度。

(7)

其中，n为时层标号。

IHX换热采用单管换热模型[14,16]，忽略传热管之间的传热差异，利用1根平均传热管开展传热分析。径向划分为管侧流体、壳侧流体及传热管3类节点，忽略轴向导热。

壳侧冷却剂热平衡方程：

(8)

传热管热平衡方程：

Psthst(Tcs-Ttu)+Ptthtt(Tct-Ttu)

(9)

管侧冷却剂热平衡方程：

(10)

其中：下标cs表示壳侧流体，ct表示管侧流体，tu表示传热管，st表示壳侧流体与传热管之间的参数，tt表示管侧流体与传热管之间的参数；P为流体和传热管之间的换热周长，m；h为流体和传热管之间的传热系数，W/(m2·K)。采用有限容积法对方程进行求解以避免IHX两侧流量失配情况下引入的数值误差。

2.2 凤凰堆分析建模

利用FR-Sdaso对凤凰堆主系统进行建模，控制体划分示于图3。H1～H9为热池控制体，其中H2为中心测量柱周围流体，H3～H7为热池主体部分，H8为热池上部区域，H9为IHX一次侧入口窗；S11、S12、S21、S22为IHX二次侧入口及出口控制体；C1～C10为冷池控制体，其中C1～C4为冷池主体部分，C5为一回路泵，C6为冷热池换热的中间控制体，C7～C10为一回路压力管。冷池内的流体经过泵进入栅板联箱后，1路向上经堆芯加热后进入热池，之后通过IHX换热后回到冷池，另1路冷却主容器壁后返回冷池。由于只有2个二回路投入运行，冷池与二回路对应划分为2组完全对称的控制体，热池则作为1组控制体。本模型中，堆芯出口温度取自堆芯区域出口控制体，未考虑堆芯出口上方区域的搅混效应，整个瞬态过程中钠池的装量和液面将因温度变化及进出口流量差而发生变化，但所有冷却剂均参与主流道循环，未考虑钠池的热分层效应及低流量情况下部分冷却剂不参与主流道循环的影响，IHX一次侧入口和出口温度均为IHX入口窗和出口窗的平均温度。

图3 凤凰堆控制体划分示意图Fig.3 Schematic of FR-Sdaso model for Phenix

图4 堆芯入口/出口温度、IHX一次侧入口/出口温度变化曲线Fig.4 Change cueves of core inlet/outlet temperature and IHX primary inlet/outlet temperature

3 结果与讨论

图4为整个实验过程中堆芯入口温度、堆芯出口温度、IHX一次侧入口温度和IHX一次侧出口温度的变化曲线，并将FR-Sdaso的计算值与实验值进行了对比。

图4a、b为堆芯入口温度(测点在泵入口处)的对比分析。实验开始后由于二回路热阱丧失，IHX二次侧入口温度快速上升，IHX一次侧出口温度随之上升(图4g)，使得冷池及堆芯入口温度快速上升，当实验转入自然循环阶段后，由于一回路热端温度逐渐下降，堆芯入口温度随之逐步下降，当二回路建立有效热阱后(3 h左右)其下降速度更快。FR-Sdaso的计算值较好地反映了整体趋势，但在500 s～3 h这段过程中，实验值呈现先快速下降再逐渐上升的趋势，而计算值则是缓慢上升之后逐渐下降。此差异的可能原因为紧急停堆后，IHX一次侧流量减少，冷池[7]部分冷却剂并未参与循环流动，IHX到泵腔处出现了“短接”，使得泵腔处测点区域温度变化与IHX一次侧出口温度趋势更为接近(即使在IHX一次侧出口温度下降后其数值仍高于堆芯入口温度测点，所以堆芯入口温度实验值上升时间更长)，而计算值给出的是考虑冷池总装量后的冷池温度，对于采用点模型串联起来的冷池，只要冷池入口温度(IHX一次侧出口温度)高于冷池平均温度，则即使入口温度下降但冷池平均温度仍会出现上升趋势，冷池平均温度在入口温度低于其时才会出现下降的趋势，也即此偏差的可能原因为程序钠池模型中所有冷却剂均参与循环而低流量下钠池内只有部分冷却剂参与主流道循环。整个瞬态过程中FR-Sdaso计算值与实验值的最大偏差约为12 ℃，文献[3]中各参与者的最大偏差范围为10～28 ℃。

图4c、d为堆芯出口温度的对比分析。在实验开始的失热阱瞬态过程中，虽然堆芯入口温度不断上升，但反应堆功率由于栅板联箱膨胀及多普勒效应等负反应性反馈而大幅下降，堆芯温升的降幅大于堆芯入口温度的升幅，因此堆芯出口温度呈现下降的趋势。在紧急停堆之后，由于一回路流量下降速度更快，堆芯温升快速上升，因此堆芯出口温度迅速升高，在自然循环建立后，堆芯出口温度则呈现逐渐下降的趋势。计算值与实验值的整体趋势符合很好，但在停堆初期的数值偏差较大，且多个系统分析程序[3,7]均出现同样的情况。堆芯出口温度测点距堆芯组件出口上方约10 cm(图1)，停堆后堆芯出口区域流量减小，测点周围出现了复杂的局部流动换热，各测点在停堆初期可能并未完全反映出温度快速上升的趋势[2]，而计算值取堆芯出口控制体温度，其未能反映堆芯出口区域的搅混效应而呈现快速上升的趋势从而与测量值出现较大偏差。停堆初期FR-Sdaso计算值与实验值的偏差约为40 ℃，文献[3]中各参与者此阶段偏差约为10～50 ℃。

图4e、f为IHX一次侧入口温度的对比分析。实验初期，堆芯出口温度下降导致IHX一次侧入口温度也即热池温度降低，由于热钠池热惯性较大，因此IHX一次侧入口温度降幅(约5 ℃)小于堆芯出口温度降幅(约30 ℃)，随后堆芯出口温度快速上升，但由于堆芯流量下降，IHX一次侧入口温度测量值并未呈现明显上升趋势，在进入自然循环阶段后，IHX一次侧入口温度不断降低。计算值在失热阱瞬态和第2阶段自然循环过程中与实验值符合较好，在自然循环建立和发展的阶段与实验值持续下降的趋势存在偏差，其原因为此阶段因堆芯流量减小热池可能出现了热分层效应[3]，堆芯出口的热钠将流向热池上部区域，而IHX一次侧入口测点距热池液面尚有一定距离(图1)，其周围流体温度可能偏低，而计算模型中钠池只考虑堆芯出口对钠池整体的加热而未考虑热分层效应，从而呈现出在堆芯出口温度低于热池平均温度前IHX一次侧入口温度一直在升高的趋势(图5，因IHX一次侧入口温度取自钠池分区模型中IHX一次侧入口窗控制体，其对热池入口温度即堆芯出口温度的变化响应略显滞后)。整个瞬态过程中FR-Sdaso计算值与实验值的最大偏差约为20 ℃，文献[3]中各参与者的最大偏差范围为13～25 ℃。

图5 IHX一次侧入口温度对比分析Fig.5 Comparison for IHX primary inlet temperature

图4g、h为IHX一次侧出口温度的对比分析。在失热阱瞬态过程中，由于IHX二次侧入口温度快速上升，IHX一次侧出口温度的计算值与实验值均呈现快速上升的趋势，且数值非常接近，紧急停堆后，由于IHX一次侧流量迅速下降，靠近IHX出口窗底部的测点(图1)周围区域流态发生了变化，此时因局部浮升力效应测点周围可能流入了原来下部冷池区域的冷钠[4]，实验值出现了短时的“阶跃”下降，而计算值给出的IHX一次侧出口平均温度则呈现缓慢下降的趋势。在之后的自然循环过程中，计算值与实验值整体趋势符合较好，但在蒸汽发生器套筒风门打开后，计算值较实验值下降得更快，可能与此阶段对自然循环流量估计值偏大有关，由于IHX为一回路最为重要的冷源，因此其他几个参数的下降速度也呈现计算值略大于实验值的特点。整个瞬态过程中FR-Sdaso计算值与实验值的最大偏差约为12 ℃，文献[3]中各参与者的最大偏差范围为10～15 ℃。

图6为FR-Sdaso计算的整个实验过程中的堆芯流量。在紧急停堆8 s后，一回路泵停运，堆芯流量快速下降，610 s时，泵转速为0，此时一回路无强迫循环压头，由于系统冷热端存在温差而出现自然循环，堆芯流量出现短时快速上升之后短暂下降并再次回升的趋势(610～800 s之间)，之后维持在50～60 kg/s。自然循环初期堆芯区域作为热端其温度变化迅速，直接影响了驱动力的变化趋势，因此堆芯流量在610～800 s之间呈现的变化趋势与堆芯出口温度类似。当蒸汽发生器套筒风口打开，二回路建立有效热阱后，IHX排热能力增加，一回路自然循环能力明显增强，堆芯流量随之快速上升，之后由于系统逐渐冷却，堆芯流量呈现缓慢下降趋势，但数值变化很小。由于实验过程中并未测得堆芯流量，无法开展对比分析，但其变化趋势却能反映实验进程的特点，同时FR-Sdaso流量计算结果落在了文献[3]中其他程序计算结果的范围之内，也从侧面反映了程序计算结果的合理性。

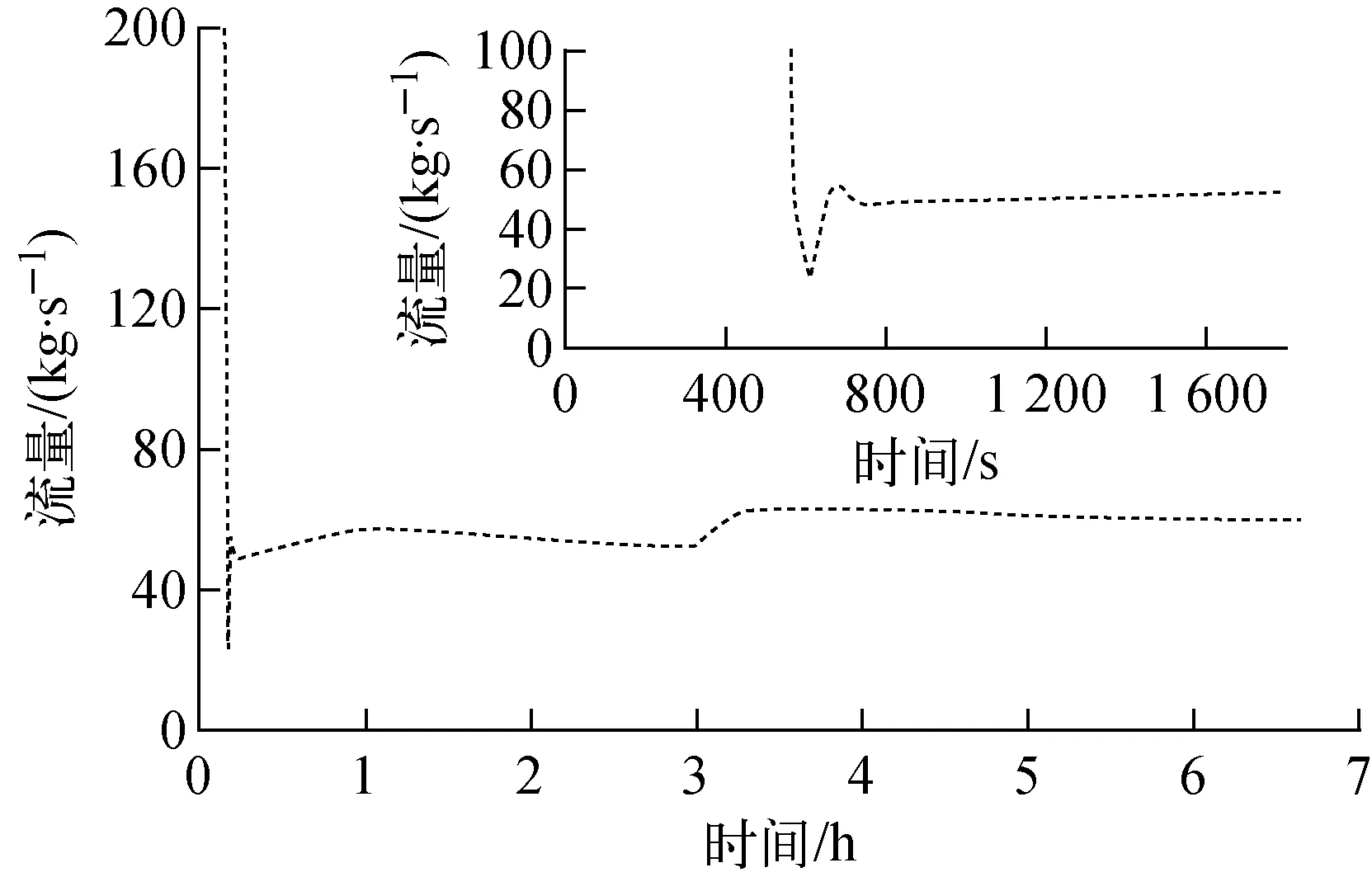
图6 堆芯流量计算结果Fig.6 Prediction of core flow rate

4 结论

本文利用FR-Sdaso对凤凰堆进行建模，并对自然循环实验瞬态过程进行了计算分析。结果表明，FR-Sdaso程序可较好地模拟实验过程中主要参数的瞬态变化趋势，并能清晰地反映失热阱瞬态、二回路无热阱及二回路建立有效热阱后的自然循环过程的特点，还可对一回路失去强迫循环后的流量变化过程进行预测。计算值与实验值的偏差主要来自两方面：一是本次系统建模只关注了关键区域的平均参数且未考虑低流量时钠池参与主流道循环的冷却剂可能变少及热分层等效应的影响；二是实验过程中测点周围的流动换热特性与正常运行时存在差别，测量值不仅反映了瞬态过程的整体变化趋势，同时反映了某些局部效应的影响，若要精确地模拟此类现象，需将系统分析程序与三维程序结合起来开展分析。

总体而言，FR-Sdaso程序可较为可靠地模拟此实验的瞬态过程，能用于模拟反应堆系统瞬态过程中的关键节点参数，可为钠冷快堆的安全分析提供重要支撑。