结霜初期超疏水表面液滴生长的规律

赵伟，梁彩华，成赛凤，罗倩妮

(东南大学能源与环境学院，江苏南京，210096)

空气源热泵在冬季制热运行时不可避免地会出现结霜现象。霜层的存在将严重影响室外空气与翅片管换热器之间的传热，降低机组效率，影响室内供热[1-3]。为了解决结霜问题，国内外学者进行了大量研究。WANG等[4]设计了一种带有固体干燥除湿装置的换热器，其可对换热器入口空气进行降湿。同时，该系统利用蓄能装置对干燥剂进行再生处理，在环境温度为-3 ℃、相对湿度为85%时，该系统在加热模式下可保持蒸发器无霜32 min。KOBAYASHI 等[5]观察到，磁场可破坏霜晶成核进而抑制霜层生长。近年来，通过对表面进行超疏水处理来影响结霜的研究较多。FENG等[6-7]研究表明，经过表面改性后的超疏水铝表面，相较于普通铝表面，在结霜初期，凝结液滴会发生合并弹跳现象，实现表面液滴的自清除，因而霜层出现的时间更晚，霜层厚度更低。同时，LIU等[8]通过研究发现，超疏水表面的霜层在融化过程中由于较低的黏附力会整块脱离表面，大大降低除霜时间和除霜功耗，提升除霜效率。因此，超疏水表面在抑制结霜和高效除霜方面具有一定的优势。超疏水表面可一定程度地延缓结霜，但并不能彻底阻止霜层的生长。在常规空气源热泵结霜过程中，要经历液滴凝结、液滴冻结、霜层生长等过程[9]。而液滴的生长是霜层形成的基础。因此，研究超疏水表面的液滴生长过程对全面揭示霜层的形成与生长具有较重要的意义。关于液滴生长的理论分析，一些学者开展了相关工作[10-13]。MILJKOVIC 等[14]研究了纯蒸气中液滴的生长，考虑了翅片表面具体的微纳结构，对润湿状态不同的液滴进行了详细建模分析。RYKACZEWSKI[15]采用CB(接触面积不变)和CCA(接触角不变)2种不同的生长模型对液滴生长进行了研究。吴晓敏等[16]采用热阻分析法建立了疏水表面液滴生长的传热传质模型，并通过实验过程中追踪的某时刻的最大液滴来验证了其模型的准确性。综上所述，目前关于液滴生长的研究主要集中在纯蒸气条件下，而关于湿空气中液滴生长的研究相对较少。由于湿空气中霜层的形成是由凝结液滴冻结而来，故而结霜初期液滴的生长对后期霜层的形成有重要影响。为此，本文作者针对湿空气中结霜初期超疏水表面液滴的生长开展理论建模，重点研究并揭示表面接触角、面积分数、基底温度以及空气相对湿度对液滴生长过程的影响规律。

1 液滴生长模型

针对结霜工况下超疏水表面液滴的生长进行理论建模，并对模型作如下假设：

1)只考虑液滴成核以后的生长过程，液滴成核过程不在本文考虑范围之内。

2)只考虑单个液滴生长，不考虑液滴合并。

3) 不考虑周围液滴对某一观察液滴生长的影响。

本文主要考察翅片在水平状态下的液滴生长过程。超疏水翅片表面的液滴在结霜工况下发生合并之前，其尺度往往很小，仅有几十微米。在这一尺度下，液滴在翅片表面承受的最大黏附力大于其自身重力，即使翅片处于竖直状态，液滴也不会在自身重力作用下发生滑落[17]，因此，翅片在水平状态和在竖直状态下区别不大，且翅片在水平放置时更便于观察，故而本文只考虑翅片在水平状态下的液滴生长过程而不再考虑翅片在竖直状态下液滴的生长过程。

由于湿空气中水蒸气含量较少，因而大量的不凝性气体对水蒸气凝结过程有很大影响。图1所示为湿空气中水蒸气凝结时热质传递示意图。根据AOKI等[18]的研究，湿空气中水蒸气凝结时的热质传递过程主要分为3层：液滴-翅片层、Knudsen层以及主流连续区层。由于表面特性对结霜初期液滴行为有较大影响，因此，本文在ZHENG 等[19]研究的基础上，特别将表面特性纳入液滴生长过程的研究之中。

1.1 液滴-翅片层

液滴-翅片层主要涉及水蒸气凝结时的热量传递，凝结热量Q将通过液滴本身和翅片结构导走，其可表示为

式中：Q为单位时间内水蒸气凝结时传递给液滴的凝结热量，W；Ts和Tb分别为液滴的表面温度以及基底温度，K；Rdrop，Rwe和Rc分别为液滴内部导热热阻、表面微结构热阻以及翅片导热热阻，K/W。

液滴内部导热热阻Rdrop可表示为[20]

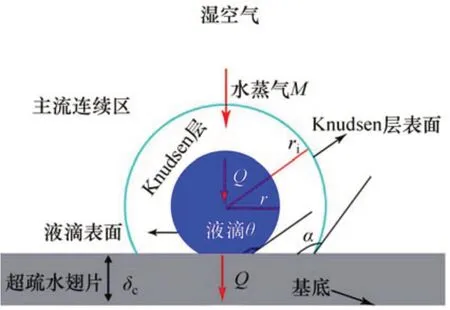
图1 湿空气中水蒸气凝结时热质传递示意图Fig.1 Schematic diagram of heat and mass transfer when water vapor condensing in wet air

式中：r为液滴半径，m；θ为表面接触角，rad；kl为液滴导热系数，W/(m∙K)。

实际固体表面在微观视角下并非光滑平坦的表面，液滴与固体表面的实际接触面积不等于液滴在固体表面的表观接触面积。定义面积分数S为液滴与固体表面的实际接触面积与表观接触面积的比值。假设液滴处于Cassie状态，表面微结构中充满截留空气，则表面微结构热阻Rwe可表示为

式中：δwe为微结构的高度，m；S为面积分数；kwe为微结构的导热系数，W/(m∙K)；ka为空气的导热系数，W/(m∙K)。

翅片导热热阻Rc为

式中：δc为翅片厚度，m；kc为翅片的导热系数，W/(m∙K)。

则从湿空气中进入液滴的总水蒸气质量流量M可表示为

式中：L为水蒸气的凝结潜热，J/kg。

1.2 Knudsen层

AOKI 等[18]的研究表明，Knudsen 层的厚度与水蒸气-干空气混合物的平均自由程具有相同的数量级，应用动力学理论来计算通过Knudsen层传递的总水蒸气质量流量，同时，考虑表面特性的影响，总水蒸气质量流量M又可表示为[19]：

式中：εc和εe分别为凝结系数与蒸发系数，εc=εe，且与接触角有关，接触角越大，其值越小，约为10-4数量级[21]；M1和M2分别为流向液滴的水蒸气质量流量以及流出液滴的水蒸气质量流量，kg/s；ri为Knudsen 层的半径，m；ρv,i和ρv,s分别为Knudsen层表面以及液滴表面水蒸气的密度，kg/m3；Rv为水蒸气的气体常数，J/(kg ∙K)；Ti与Ts分别为Knudsen层表面以及液滴表面的温度，K。

ri可表示为

式中：β为常数；λ为湿空气分子的平均自由程，m。

λ可表示为

式中：μm为主流湿空气的动力黏度，kg/(m·s)；Rm为主流湿空气的气体常数，J/(kg∙K)；Tm为主流湿空气的温度，K；pm为主流湿空气的压力，Pa。

液滴表面水蒸气的密度ρv,s可由下式求出：

式中：pv,s为液滴表面水蒸气压力，Pa。

Knudsen层表面水蒸气的密度ρv,i为

式中：pv,i为Knudsen层表面水蒸气压力，Pa；液滴表面和Knudsen层表面水蒸气压力均按饱和水蒸气压力处理。

联立式(6)～(8)可得：

式(13)所示为液滴表面流向主流空气的水蒸气质量流量，实际计算时取相反数。

1.3 主流连续区层

在主流连续区层中，水蒸气分子与不凝性气体分子的运动满足流体力学定律与扩散定律。

湿空气由水蒸气和不凝性气体组成，其密度ρm可表示为

式中：ρv和ρa分别为湿空气中水蒸气的密度与不凝性气体的密度，kg/m3。

湿空气中的不凝性气体无法凝结，则有：

式中：um和uv分别为湿空气的主体速度以及水蒸气的相对速度，m/s。

进入液滴的总水蒸气质量流量M可表示为

式中：α为Knudsen 层表面与翅片表面相交处的切线与翅片表面的夹角，如图1所示。

根据扩散传质的斐克定律，有：

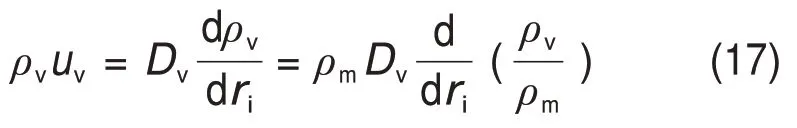
式中：Dv为水蒸气在空气中的扩散系数，m2/s。由于传质方向与坐标轴方向相反，故菲克定律中的负号略去。

联立式(9)和(15)～(17)，有：

式(18)从r∞积分到ri得：

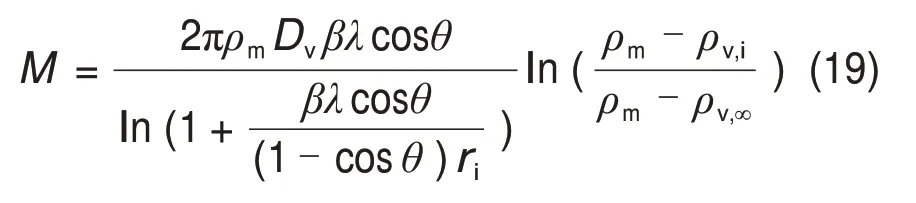
式中：ρv,∞为主流湿空气中的水蒸气密度，kg/m3。

以上方程中，各未知数均是液滴表面温度Ts和Knudsen 层表面温度Ti的函数。联立式(5)，(13)和(19)，通过迭代计算即可得出Ts和Ti，进而获得湿空气传递给液滴的总水蒸气质量流量。

液滴的生长速率G可表示为

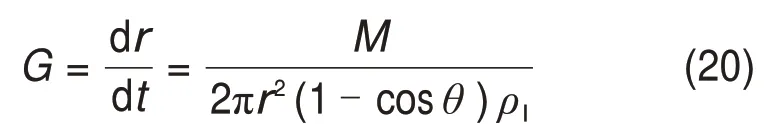
式中：ρl为液滴的密度，kg/m3。通过数值方法求解式(20)即可获得液滴半径r与时间t的关系。

液滴的成核半径rmin[22]为

式中：Tsat为水蒸气分压力对应下的饱和温度，K；σlv为液滴的气液界面张力，N/m；L为水蒸气的凝结潜热，J/kg。为方便计算，t=0 s时的初始半径可取2～10倍的成核半径，其对计算结果影响不大。

2 实验数据与模拟数据对比

为验证所建理论模型，在湿空气温度Tm=27.3 ℃，相对湿度φ=59.7%，基底温度Tb=-5 ℃，翅片表面接触角θ=159°，面积分数S=0.13 的条件下进行实验。图2所示为液滴生长过程中液滴半径的实验数据与模拟数据的对比以及液滴1 的生长状态。

图2 理论模型与实验结果对比图以及液滴1的生长状态Fig.2 Comparison of theoretical model and experimental results and growth state of droplet 1

由于液滴刚开始形成时，尺度太小，无法测量。故从实验计时开始后经过40 s 开始观察测量，当某一所观察的液滴发生合并时，该液滴观察测量过程结束。如图2所示，本文观察并统计4个不同液滴在合并之前的半径。由图2可知：模拟数据表明，在所观察的时间段内即液滴合并之前，液滴半径与时间近似呈线性关系(曲线斜率略微下降)。经过一段时间之后，实验数据与模拟数据的偏差略有增大，主要原因是：随着时间的增加，超疏水表面上的液滴尺寸越来越大，液滴之间的距离越来越接近，相邻液滴之间对于水蒸气分子存在竞争关系，导致实际液滴的生长速率较理论模型更慢，故而偏差增大。

图3和图4所示分别为在湿空气温度Tm=27.3 ℃，相对湿度φ=59.7%，基底温度Tb=-5 ℃，翅片表面接触角θ=159°，面积分数S=0.13 的条件下计算得到的在不同时刻从湿空气中进入液滴的总水蒸气质量流量M以及液滴在不同时刻的生长速率G。由图3可知：随着时间t的推移，进入液滴的总水蒸气质量流量M逐渐增大。这是由于，随着时间的增加，液滴半径逐渐增大，导致液滴外表面积增加，液滴外表面积增加即传质面积增加，因而进入液滴的总水蒸气质量流量也随之增加。

图3 进入液滴的总水蒸气质量流量M随时间t的变化关系Fig.3 Relationship between total mass flow rate of water vapor entering droplets with time

图4 液滴的生长速率G随时间t的变化关系Fig.4 Relationship between growth rate of droplets with time

从图4可知：液滴的生长速率G随着时间t的推移逐渐下降。这主要是因为，由式(20)可知，随着液滴半径的增大，液滴外表面积虽会增大进而增加水蒸气的传质量，由于水蒸气传质量的增加幅度小于液滴外表面积的增加幅度，因而导致液滴生长变慢，但在所观察的时间段内，液滴生长速率下降的幅度并不大。

从图1所示的物理模型可知：水蒸气凝结时传热传质过程分为3 层，即液滴-翅片层、Knudsen层以及主流连续区层，这3个部分的温差共同组成整个基底过冷度ΔT(ΔT=Tm-Tb)。图5所示为在液滴生长过程中，各层温差(即液滴-翅片层温差ΔT1=Ts-Tb，Knudsen 层温差ΔT2=Ti-Ts，以及主流连续区层温差ΔT3=Tm-Ti)所占基底过冷度的比例随时间的变化规律。由图5可知：在所研究的时间段内，随着时间的增加，各层温差占基底过冷度的比例变化很小。且各层温差占基底过冷度的比例从大到小依次为：Knudsen 层温差、主流连续区层温差、液滴-翅片层温差。其中，Knudsen 层以及主流连续区层，这2 部分的温差占基底过冷度的95%以上。

图5 各层温差占基底过冷度的比例随时间t的变化规律Fig.5 Variation of proportion of temperature difference of each layer to subcooling degree of substrate surface with time

3 液滴生长规律

3.1 表面接触角对液滴半径变化的影响

图6所示为在湿空气温度Tm=27.3 ℃，相对湿度φ=59.7%，基底温度Tb=-5 ℃，翅片表面面积分数S=0.13的条件下3种不同接触角表面的液滴半径r随时间t的变化规律。由图6可知：接触角越大，即表面疏水性能越好，液滴半径变化越慢。当表面接触角由79°增加至159°时，108 s后，液滴半径由约50.3 μm降为约19.9 μm。

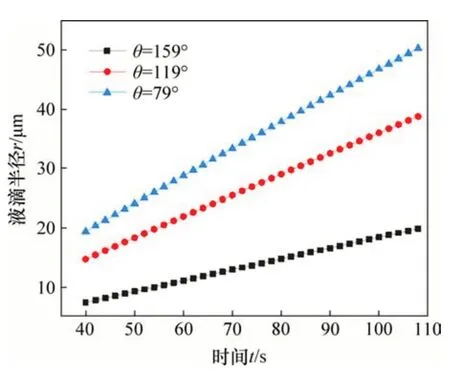
图6 不同接触角表面液滴半径r随时间t的变化规律Fig.6 Variation of droplet radius with time on different contact angle surfaces

为探究其具体原因，分析不同接触角表面主流连续区层温差占基底过冷度的比例情况(即ΔT3/ΔT)，如图7所示。在主流连续区层内，水蒸气以扩散形式传递，从图7可以看出，接触角越大，主流连续区层温差占基底过冷度的比例越小，意味着主流湿空气与Knudsen层表面的温差越小。而温度又与饱和湿空气的含湿量成正相关，在主流湿空气温湿度保持不变的情况下，意味着Knudsen层表面与主流湿空气含湿量的差值越小，使得主流连续区层内的扩散传质能力减弱，因此，液滴的生长速率变缓。

图7 不同接触角表面ΔT3/ΔT随时间t的变化规律Fig.7 Variation of ΔT3/ΔT on different contact angle surfaces with time

3.2 面积分数对液滴半径变化的影响

图8所示为在湿空气温度Tm=27.3 ℃，相对湿度φ=59.7%，基底温度Tb=-5 ℃，翅片表面接触角θ=159°时，不同面积分数S下的液滴半径r随时间t的变化规律。从图8可知：在不同面积分数S下，液滴半径的变化规律近乎一致。

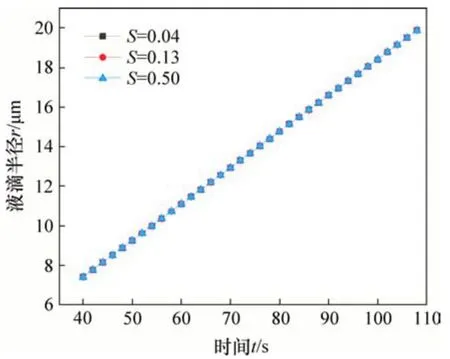
图8 不同面积分数下液滴半径r随时间t的变化规律Fig.8 Variation of droplet radius with time under different area fractions

图9 Rwe占液滴-翅片层总热阻的比例随时间t的变化规律Fig.9 Proportion of Rwe to total thermal resistance of droplet-fin layer with time

分析其原因，因面积分数S越小，表示液滴与翅片表面的实际接触面积越小。与面积分数S相关的热阻Rwe占整个液滴-翅片层总热阻的比例(即Rwe/(Rdrop+Rwe+Rc))如图9所示。从图9可知：Rwe占液滴-翅片层总热阻的比例随面积分数S减小而增大，但因翅片表面微纳结构尺度太小，导致Rwe所占总热阻的比例较低，当S从0.50降到0.04时，其所占液滴-翅片层总热阻的比例仅从约0.018%升高到约0.2%，这是图8中3条曲线近乎重合的原因。

3.3 基底温度对液滴半径变化的影响

图10所示为在湿空气温度Tm=27.3 ℃，相对湿度φ=59.7%，翅片表面接触角θ=159°，面积分数S=0.13 时，基底温度分别为-5，-11 和-17 ℃下液滴半径r随时间t的变化规律。

由图10可知：随着基底温度的降低，液滴生长加快。其原因为：在其他条件相同的情况下，随着基底温度的降低，相变驱动势增大，湿空气中的水蒸气更易凝结，因而液滴生长加快。当基底温度由-5 ℃降至-17 ℃，108 s后，液滴半径由约19.9 μm升至约24.5 μm。

图10 不同基底温度下液滴半径r随时间t的变化规律Fig.10 Variation of droplet radius with time at different substrate temperatures

3.4 空气相对湿度对液滴半径变化的影响

图11所示为在湿空气温度Tm=27.3 ℃，基底温度Tb=-5 ℃，翅片表面接触角θ=159°，面积分数S=0.13时，不同空气相对湿度下的液滴生长规律。

由图11可知：随着空气相对湿度的增大，液滴的生长速率加快。这是因为，在其他条件相同的情况下，随着空气相对湿度的增大，通过扩散传递的水蒸气的量将加大，液滴生长速率也随之加快。当空气相对湿度由59.7%升至79.7%时，108 s后，液滴半径由约19.9 μm升至约30.3 μm。

图11 不同空气相对湿度下液滴半径r随时间t的变化规律Fig.11 Variation of droplet radius with time under different relative humidity of air

4 结论

1)建立湿空气中结霜初期超疏水表面液滴生长的分层模型并进行模型验证。研究表面接触角、面积分数、基底温度以及空气相对湿度对液滴生长的影响规律。

2)Knudsen层以及主流连续区层温差所占基底过冷度的比例较大，液滴-翅片层温差占基底过冷度的比例较小。其中，Knudsen层以及主流连续区层这2 部分的温差所占基底过冷度的比例达到了95%以上。

3)在其他条件相同的情况下，随着表面接触角的增大，由于主流连续区层温差减小而导致液滴生长逐渐变慢。当表面接触角由79°增加至159°时，108 s 后，液滴半径由约50.3 μm 降为约19.9 μm。与面积分数S相关的热阻Rwe由于占液滴-翅片层总热阻的比例较小，当S=0.04时，Rwe占液滴-翅片层总热阻的比例约为0.2%，因而面积分数S对液滴生长的影响较小。

4)在其他条件相同的情况下，随着基底温度的降低，相变驱动势增大，液滴生长速率也随之加快。当基底温度由-5 ℃降至-17 ℃，108 s 后，液滴半径由约19.9 μm 升至约24.5 μm。空气相对湿度越大，水蒸气扩散传质越快，液滴生长也越快。在其他条件相同的情况下，当空气相对湿度由59.7%升至79.7%时，108 s 后，液滴半径由约19.9 μm升至约30.3 μm。