CFR600假想堆芯解体事故钠泄漏量评估与计算

孙博文，喻 宏

(中国原子能科学研究院，北京 102413)

假想堆芯解体事故(Hypothetical Core Disruptive Accident，HCDA)虽然是一种概率极低的假想事故，但因其后果十分严重，所以仍被国际公认为核安全事故分析中需要考虑的、最为危险的快堆事故之一。[1]该事故的直接后果之一是主容器中的钠冷却剂向外泄漏。若安全壳的容积不足以容纳泄漏的钠，会导致放射性物质向环境释放。因此，对HCDA过程中钠泄漏量的计算是十分必要的。

目前，国际上对钠泄漏量计算所采用的方法可分为三种。其一是通过经验公式确定局部和摩擦阻力等参数，进行理论计算；其二是建造等比例模型并采用替代品材料，进行模型实验；其三是通过建模和数值计算软件进行计算。一些研究者采用了三种方法对印度PFBR的HCDA钠泄漏量进行了详细的研究和计算[2-4]。

本文对中国600 MW示范快堆进行研究计算，通过分析其在HCDA情况下的钠泄漏途径，构建其流道模型，通过计算流体力学的方法，利用FLUENT软件对各流道的钠泄漏量进行计算与评估，总结一种HCDA钠泄漏量计算的方法，并通过计算结果为后续的安全分析工作提供依据和参考。

1 计算模型与方法

1.1 计算模型

1.1.1 反应堆结构简介

中国600 MW示范快堆以钠作为冷却剂，采用池式布置。主容器的顶部为锥形瓶口状，中间装有多层嵌套的旋塞结构。钠泵与热交换器等结构分布在堆芯周围，并贯穿主容器顶部的锥面，并与之互相嵌套。在多层的旋塞之间，以及旋塞、堆内组件与主容器之间存在微小的空隙，其顶端采用锡铋合金密封，以隔绝空气、水等物质进入反应堆。由于旋塞易于活动，且该部分结构间空隙的直径和宽度均明显大于其他空隙，故仅对旋塞间的部分空隙构建流道进行计算。

1.1.2 流道构建

本文所研究的流道共有三条，分别为大旋塞与堆容器法兰环、中旋塞与大旋塞、小旋塞与中旋塞之间的空隙所构成的流道(以下分别称为大、中、小流道)。三条流道的示意图如图1所示，其相关参数如表1所示。由于三条流道在几何上各自关于其中心轴线具有高度的对称性，为了使计算简便可行，采用了二维的轴向切面作为流道模型，并添加轴向对称的几何条件。

表1 流道尺寸参数Table 1 Size parameters of flow paths mm

图1 流道结构示意图Fig.1 Structural diagrams of flow paths

1.1.3 网格划分

本文使用ICEM CFD软件，设置不同的网格密度，对上述三条流道按结构化网格进行划分。网格质量大于0.99，偏斜度大于0.70。

1.2 FLUENT仿真计算

1.2.1 数值模拟方法

本文湍流模型采用SSTk-ω模型，近壁面处理选取标准壁面；采用压力基求解器并选择瞬态时间格式；其余采用默认设置。

1.2.2 基本假设与边界条件

由于HCDA过程非常短暂，不考虑此过程中的温度变化，因此本文中所进行的计算均是基于绝热条件下考虑的，涉及物性参数的温度恒定为723 K。设定钠为不可压的流体，其密度恒定为844.3 kg/m3，黏度系数为0.000 3 kg/m·s。

在实际情况下，旋塞会随着内部压力的下降而回落，从而导致流道被关闭，泄漏停止。本文采用了一种保守的假设，即认为直到1 s的时刻，流道一直保持正常开启的状态，故在计算中将泄漏量的统计时间范围设定为0～1 s。

在本文中，流道入口和出口均采用压力边界条件。入口处采用能量释放为100 MJ的HCDA压力脉冲，该压力值随时间的变化如图2所示，出口处的大气压力恒定为0.1 MPa。各壁面选择非滑移边界条件。

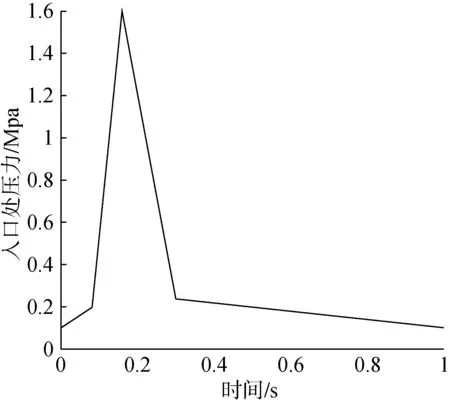
图2 入口压力变化图Fig.2 Variations of inlet pressure

2 数值计算的可靠性验证

对于瞬态数值模拟，首先要确认计算结果与网格数量、时间步长等参数是无关的，即需要验证网格与时间步长的无关性，以保证计算的可靠性。本文主要探讨模拟计算结果中流动速度的无关性检验，特别是不同条件对流速最大值的影响。

2.1 网格无关性检验

按时间步长0.000 1 s，对4组不同密度的网格进行无关性检验(网格具体参数如表2所示)。由于考虑到窄流道问题，以截面网格数作为区分这些网格密度的主要参数。检验的时间区间范围为从初始时刻开始到流速达到最大值后的一小段时间为止。

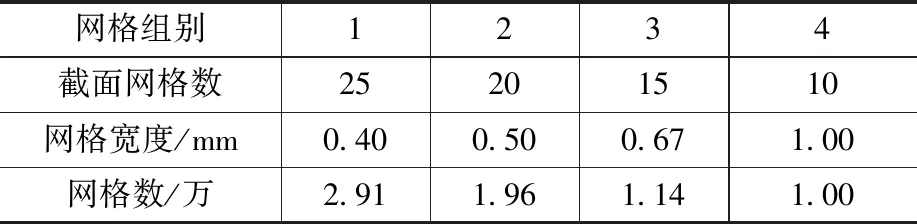
表2 网格无关性检验参数Table 2 Parameters of grid independence verification

由图3所示，网格密度(数量)对计算结果有着较为轻微的影响。网格较密时(第1～3组)，增加网格密度，流速几乎不发生变化。认为截面网格数大于15时结果差异不大。而网格稀疏时(如第4组)，相对于第1～3组，流速有着先高后低的偏差，其偏差值在5%以内。为了更明确地表现采用不同疏密程度的网格对计算结果的影响，选择0.20 s这一不同网格计算结果偏差最大的时刻，将其相关数值如表3所示。

图3 流速变化图Fig.3 Variations of velocity

表3 0.20 s时刻各网格组别对应的泄漏率Table 3 Leakage rates of different meshing groups at 0.20 s

可以发现，当截面网格数大于15时，其结果已经收敛。因此，可以认为网格的划分方案已经满足无关性的要求。在后续的计算中，以第2组作为网格划分的标准，并重新构造大、中流道网格。二者的网格数量分别为3.66万和2.99万。

2.2 时间步长无关性检验

在入口压力变化较快以及流速较高的阶段(0.08～0.22 s)，按照5种不同的时间步长组合方案，对上述第2组网格进行时间步长无关性检验。该5种方案为在3个不同的阶段(0.08～0.11 s、0.11～0.14 s和0.14～0.22 s)分别采用不同的时间步长，具体方案表4所示。

表4 时间步长无关性检验参数Table 4 Parameters of time step independence verification

由图4所示，不同的时间步长对计算结果有着一定的影响。在计算结果上，各种方案的误差范围在7%以内。当时间步长较大时，流速变化较迅速；时间步长较小时，流速变化较缓慢，达到最大流速的时间点也会向后推迟。这种流速的变化趋势会随着各阶段时间步长的细化而逐渐收敛。特别地，通过对方案4和方案5的比较可以发现，若仅在压力快速变化初期(阶段1)采用较长的时间步长，会使中期(阶段2)的流速略微增加，但在后期(阶段3)趋于一致。这种偏差相比于方案1至方案3的偏差较小。

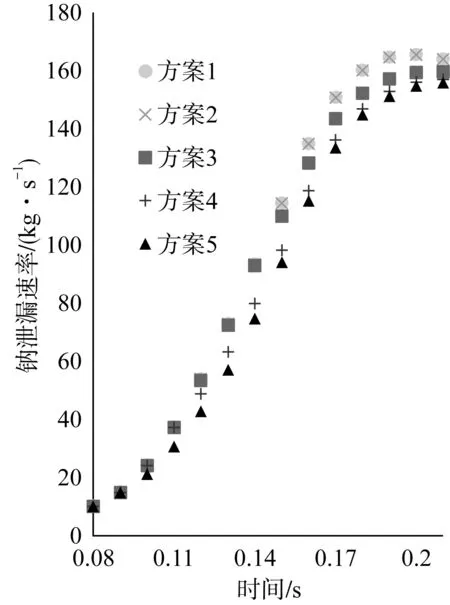
图4 流速变化图Fig.4 Variations of velocity

在后期的计算中，在考虑计算经济性的前提下，采用方案4的时间步长，并依据0.22 s之后的流速变化趋势确定相应各时段的时间步长。

综合以上的无关性检验结论，可以论证数值计算方法能够解决本文中问题，并得出可信且更为精确的结果。

3 计算过程与结果

在最初阶段(约0～0.08 s)，由于主容器内部压力变化较为缓慢，流道内钠的流速未有明显的增加。自0.08 s开始，流速随着压力脉冲的开始而迅速增加。不同的流道在约0.17～0.21 s时，其泄漏速率达到最大值。此后，HCDA过程趋于结束，流速也缓慢减小。

在直管段中(包括出口之前)，速度充分发展，而局部高速点出现在管道弯曲段结束后、开始进入长直管道处。以小流道为例，可以发现，在0.21 s达到最大速度时，充分发展段的中心处流速约为23 m/s，局部最高速度则超过45 m/s，如图5所示。

图5 小流道0.21 s时速度空间分布图Fig.5 Contour of velocity of small flow path on 0.21 s

在三条流道中，钠泄漏速率的变化趋势基本一致，其数值主要取决于各流道的出口横截面积。钠泄漏速率与泄漏量随时间变化的曲线如图6所示。

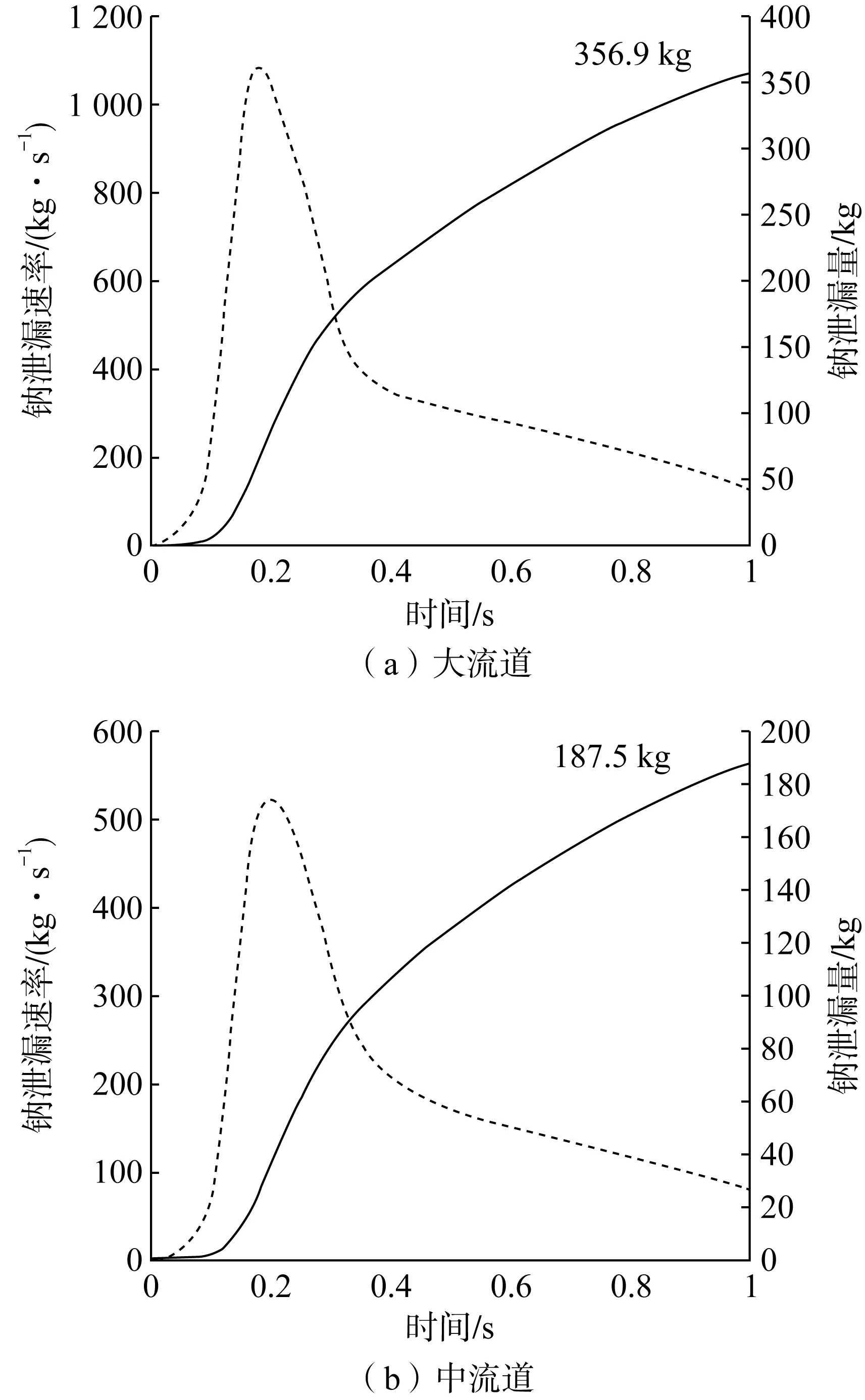
图6 三条流道钠泄漏速率与泄漏量变化图Fig.6 Variations of velocity and sodium leakage of 3 flow paths

通过FLUENT进行模拟计算所得的1 s内钠泄漏总量为601.4 kg，其中大流道356.9 kg，中流道187.5 kg，小流道57.0 kg。该计算结果基于单相流体的情况，是一个较为保守的结果。

4 结论

本文对HCDA过程中的钠泄漏计算开展了泄漏途径分析、流道模型建立与二维化处理以及网格划分、边界条件确定等初始工作，并通过网格无关性检验与时间步长无关性检验，论证了数值计算的可靠性，并采用了一种较为精确的计算方案。通过FLUENT进行模拟计算所得的1 s内钠泄漏总量为601.4 kg，其中大流道356.9 kg，中流道187.5 kg，小流道57.0 kg。由于该计算结果基于单相流体，未考虑主容器中存留的氩气，故结果是较为保守的。在后续的研究计算中，将对多相流体情形进行进一步探讨。