浅谈“对应”与“顺序”原则在《全等三角形》一章中的应用

杨绍政

【摘 要】推理是《全等三角形》一章中的重点兼难点，是学好数学的分水岭，掌握“对应”与“顺序”原则，在一定的程序和规则的反复训练，就是多少人苦苦寻觅的推理妙法。

【关键词】全等三角形;对应;顺序

数学学习中，很多知识具有一定的逻辑性与严谨性。掌握它，学习就会变得轻松而有规律，反之，只会学习吃力，事倍功半，丧失学习兴趣，成绩情况可想而知。

《全等三角形》一章，推理是本章的重点兼难点，是继《相交线与平行线》中简单推理的飞跃，学习本章，学生的推理思路将变得清晰，逻辑思维能力进一步增强，也为今后更深层次学习数学奠定基础，同时也是学好数学的分水岭，此部分知识若能平稳过渡，今后学好数学是轻而易举的事;相反，今后要学好数学，可能性不大。现从“对应”与“顺序”原则在《全等三角形》一章中的应用，谈谈推理的一些微妙之处。

现行人教版初中数学教材《全等三角形》中第一个完整的证明题是P36的例1。题目为：如图△ABC是一个钢架，AB=AC，AD是连接点A和BC中点D的支架，求证：△ABD≌△ACD.

從证明过程可以看出，推理三角形全等是具有严格的框架的，把握关键步骤很重要。即③“在△×××和△×××中”属关键的第一步;大括号④—⑥属关键的第二步，具体有三个符合判定的条件组成，如果不属于已知条件或隐含条件的，必须在③之前事先推出;⑦“△×××≌△×××（×××）”属关键的第三步。熟记③—⑦这一基本框架，是学好三角形全等证明的大前提，这一框架中还必须把握的是“对应”和“顺序”原则，即“和、=、=、=、≌”左侧应是同一个三角形或同一个三角形的元素，右侧应是另一个三角形或另一个三角形的元素，且每处都是对应顶点的字母必须写在对应的位置上，可简记为“左右对应统一”，大括号里的三条件必须按判定进行书写，如涉及“SAS”判定，意味着第一行写边，第二行写角，第三行写边，涉及“HL”判定，则大括号内第一行写斜边，第二行写直角边，其它依次类推，可简记为“上下注意顺序”。

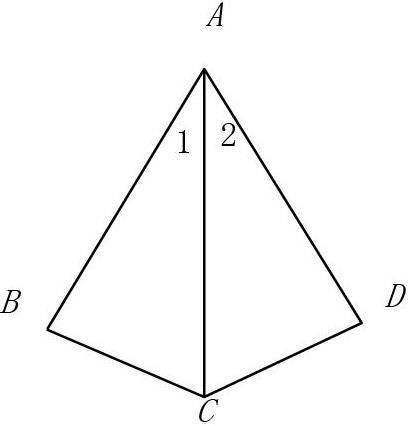
又如P41的练习题第1题。题目为：如图，AB⊥BC，AD⊥DC，∠1=∠2.求证AB=AD.

结合前例及本例证明过程可以看出，“左右对应统一”、“上下注意顺序”均把握的非常到位，此题用到的是“AAS”判定定理，第一个“A”与“S”是“对”的关系，即边是角的对边，角是边的对角，将④和⑤换位置，就不是“AAS”，将⑤和⑥换位置，也不是“ASA”，这是很多同学证明时，极易弄错之处。很多同学常易将条件满足“AAS”判定的误用为“ASA”，将条件满足“ASA”判定的误用为“AAS”，甚至条件满足“HL”判定的误用为“SAS”，或干脆发明创造“SSA”或“ASS”，实乃犯顺序之病也。事实上，三角形的组成元素包括三个顶点、三个角和三条边，判定三角形全等用到的是边、角，我们应该把已知、隐含或已证等条件在三角形中醒目地标识出来，然后结合判定定理按顺时针或逆时针的顺序进行梳理，涉及两角一边的，从角开始，推敲一下是“ASA”还是“AAS”，涉及两边一角的，从边开始，先考虑“HL”（若有直角）再考虑“SAS”。

《全等三角形》是初中数学三大难点之一，这里的难点要解释为转折、重要和提醒之意，而非传统的难点，但必须坚决突破。也许你在初一时的数学成绩很一般，某些知识还处在混乱，甄别能力较弱，可一旦用心地学了《全等三角形》一章后，逻辑思维能力必将增强，推理能力一定提高。这样，思路越来越清晰，知识体系逐步向完整靠拢，整体数学素养将是一次不小的飞跃，乐学和自主学习方面就会呈现新的良性局面。

“对应”与“顺序”原则作为数学学习中必备的素养，应在初中数学学段的教学中逐步渗透，在恰当的时机全盘托出并掌握，《全等三角形》一章的推理教学属最恰当时机，教师应做好主导，科学、合理运筹，让学生掌握“对应”与“顺序”原则在推理中的微妙之处，轻松突破此难点。

总之，掌握“对应”和“顺序”原则在推理中的应用很重要。也许你还在苦苦寻觅一些推理的高招妙法，可掌握了一定的程序和规则的反复训练就是最佳方法。教师在主导课堂中，应充分利用学生的课堂作业、问题回答和检测等手段，弄清学生情况，在充分了解学生的前提下，不断发现学生在运用“对应”和“顺序”原则在推理中的易错之处，查缺补漏，争取全面提高。从《全等三角形》一章的学习中再次证明，学习只要得法，一定能学好;学习只要有人指导，一定事半功倍;学习只要步入正轨，不想学好也难。

参考文献：

[1]《义务教育课程标准实验教科书·数学》（八年级上册）人民教育出版社 2013年1月

（作者单位：云南省临沧市凤庆县第一中学）