基于地区线性矩法的水口电站流域暴雨频率分析

林智琛 杨 婷 林 艳

(福建省气象服务中心，福建 福州 350001)

暴雨洪涝是我国面临的最为严重的自然灾害之一，每年造成的损失难以估计。无论是工程或是城市，其防洪规划设计都显得尤为重要，尤其是地处湿润气候的山岳地区。在实际应用中，防洪设计标准的核心是水文频率计算，这是一种基于现有样本资料来推算总体分布的统计方法。随着近年来极端水文气象事件的频繁发生，洪水资料的一致性受到了破坏，通过暴雨频率分析来间接推求设计洪水，已成为一种实际可靠的方法[1-3]。

现阶段在我国广泛应用的频率分析方法还停留在“一点(单点、单时段)、一线(皮尔逊Ⅲ型曲线)、双眼(目估适线)”的水平[4]，这种方法侧重于单站的频率分析，而对地区整体水文气象信息的利用则研究得很少，参数估算方法的精确性和频率估计值的准确性已远不能满足我国经济建设的需要[5-7]。

美国从上世纪90年代开始采用一种全新的水文气象途径的暴雨频率计算方法——地区线性矩法，该方法认为区域暴雨分析应更侧重于区域整体性，从而提升了频率分析的精确性和准确性。基于此，美国已制订一套适合本地区自然降雨规律的多时段多频率的估算成果图集(电子版)，进行全国规范化[8-9]。英国水文研究所也基于地区线性矩法进行了洪水分析，并在此基础上重新编写了《洪水估计手册》[10]。近年来，国内一些学者也认识到了我国现阶段频率分析研究中的局限性，部分学者采用地区线性矩法对太湖流域[7]、淮河流域[11]、广西省[12]、江西省[13]和四川省[14]的全域研究。本文以福建省水口水电站流域作为研究对象，探究地区线性矩法在闽西北山岳地区的应用，从而提升水口电站流域暴雨频率分析的精确性和准确性，为后续开展暴雨风险区划研究打好基础。

1 研究区域和资料介绍

1.1 研究区域介绍

水口水电站是福建省最大的水电站，其坝址位于福州市闽清县内闽江干流上，控制流域面积达到了52438km2，占闽江全流域的86%，包含11个子流域。流域内以山地、丘陵为主，地势较高，涵盖了多个地市行政区域和多个中小型水库。流域内雨量丰沛，属于亚热带季风气候，流域内存有一个暴雨中心，同时也是地质灾害的易发区，一旦遭受暴雨洪涝灾害，后果将十分严重[15]。因此，对水口电站流域进行暴雨频率分析，对于流域内水库以及其他重大工程的防洪设计，各县市防洪防汛规划、海绵城市的规划建设以及气象防灾减灾服务都具有重要意义。

1.2 资料选取

本文选取水口电站流域内资料长度在55a以上的25个雨量站的年最大日降雨量资料。为确保研究区域边缘站点研究结果的可靠性，将流域外扩50km作为研究的缓冲区域，同时将缓冲区中省内10个雨量站以及邻省5个雨量站的年最大日降雨量资料也纳入研究，从而提高研究合理性。年最大日降雨量资料已经过质量控制，各站平均资料长度在62a。各雨量站及流域分布图见图1。

2 研究方法

2.1 地区线性矩法

地区线性矩法是一种将线性矩法地区和分析法相结合的新型频率估算方法。其中线性矩法是Hosking在概率权重矩的基础上提出的[16]，线性矩定义为次序统计量某种线性组合的期望值，它可以表达为一阶样本矩各种组合的计算[3]。线性矩的一大特点就是对序列中的极值数据没有那么敏感，因此提升了参数估计的精确性。假设X1∶n≤X2∶n≤L≤Xn∶n为样本容量为n的次序统计量，则定义其r阶线性矩变量如下：

(1)

上式中,EX(r-k)∶r是容量为n的样本中排在第r-k位次序统计量的期望值。随机变量X常用的前四阶样本线性矩可以表示为[16]：

(2)

(3)

(4)

(5)

同常规矩法类似，线性矩的统计参数表达为离差系数(L-Cv)：t=l2/l1,偏态系数(L-Cs)：t3=l3/l2,峰度系数(L-Ck)：t4=l4/l2[17]。

地区分析法使频率设计值的准确性得到提升，其核心思想是将每个站点的降雨量系列假定分为共性与特性两部分。其中，共性是指反映该地区共有的降雨特性的地区分量，在实际应用中需要在水文气象一致区分区的基础上为地区分量选配最优的无量纲频率分布曲线。而特性是指反映本站点特有的降雨特性的本地分量，各站的频率估计值需要结合本地分量和地区分量来推求，可由下式表达[7]：

(6)

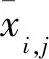
2.2 一致区的划分

综上可知，使用地区线性矩法的基础是对研究区域进行水文气象一致区的划分，在实际应用时一般遵循研究区的划定、气象相似性判定、水文相似性判定、异质性检验和不和谐度检验等原则[5]。为了使边界地带的频率设计值更为可靠，研究区域还需包含缓冲区部分，缓冲区的范围通常为子区长度一半的距离。在分区时需要考虑一致区内的各站点在气象上要具有相同的气候背景，在水文上其统计参数要在一定容忍度内[7]。

2.2.1 不和谐度检验

本文运用不和谐度检验来进行一致区的初步划分，假设片区内站点数为N，(t(i),t3(i),tr(i))为第i个站点的样本线性矩系数，则不和谐度指标为：

(7)

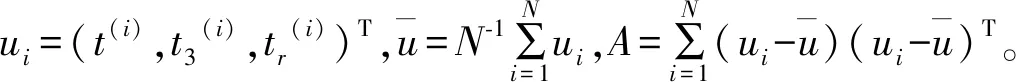
2.2.2 异质性检验

为了更好地划分一致区，Hosking提出使用异质性检验来进一步判断，计算公式如下[9]：

(8)

(9)

(10)

其中，H1为异质性检验统计量，若H1<1，表示为可接受的一致区，若1≤H1<2，表示可能的异质区，H1≥2为异质区。而当H1≤-1时，说明片区内站点间的相关性较强，需要进行样本独立性检验[7]。μV和σV为经蒙特卡洛模拟的均值和方差。t(i)和ni分别为片区内第i个雨量站历史雨量数据的长度和线性离差系数。

2.3 频率分布线型的选择

频率分布曲线的选择是地区线性矩法的重点，目前在实际应用中，3参数的分布线型能兼顾稳定性和灵活性[5]。因此本文选择广义极值分布(GEV)、广义逻辑斯蒂分布(GLO)、广义正态分布(GNO)、广义帕累托分布(GPA)和皮尔逊Ⅲ型分布(PE3)作为候补。并通过蒙特卡洛模拟、均方根误差检测和实测数据检测这3种拟合优度检测方法来确定各一致区的频率分布线型。

2.3.1 蒙塔卡洛模拟检测

统计量ZDIST表达式为[9]：

ZDIST=(τ4DIST-t4R+B4)/σ4

(11)

其中，τ4DIST为选择的分布线型的线性峰度系数，t4R为区域平均的线性峰度系数，B4为其偏差，σ4为模拟的线性峰度系数的标准差。当|ZDIST|≤1.64，则认为拟合结果合理，且|ZDIST|越接近零，拟合效果越好。

2.3.2 均方根误差检测

统计量RMSE表达式为：

(12)

其中，ni为第i个站点的资料长度，Si,L-Ck和Di,L-Ck分别为第i个站点的线性峰度系数以及在分布函数曲线上偏态系数值所对应的峰度系数值[7]。在检验中对每个候选线型都进行计算，RMSE值越小，说明分布线型为最佳。

2.3.3 实测数据检测

统计量RE表达式为：

(13)

式中，N为重现期，Fi,Tj和PTj为对应重现期下经验频率和理论概率，通过计算其相对误差来反映站点的候选线型与实测数据的拟合程度。RE值越小，说明拟合效果越好[2]。

3 结果分析

3.1 分区结果和线型选择

对研究区域内各站点进行统计参数计算，包括L-Cv和L-Cs，具体分布见图2。从图中可知，离差系数L-Cv范围在0.141～0.226，离散程度相对集中，大值区集中在流域西北部。偏态系数L-Cs范围在0.129～0.364，均呈现正偏，大值区位于流域西部。在统计参数分布图的基础上，结合流域气候特征和地形地貌等因素，大致划分为7个一致区，并对其进行异质性检验和不和谐度检验，具体结果见表1。

由表1可知，各一致区内的站点Di值均没有超过临界值，均通过不和谐度检验。从异质性检验结果来看，7个一致区的H1值均小于1，说明初步划分7个一致区为可接受的一致区。但区域6、区域7的H1值小于-1，说明该区域内的站点可能存在较强的相关性，需要进行进一步的相关性检验。

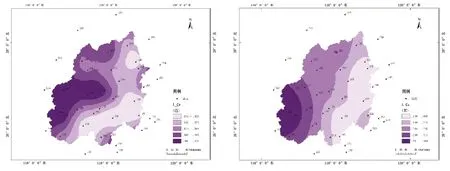
(a)L-Cv分布 (b)L-Cs分布

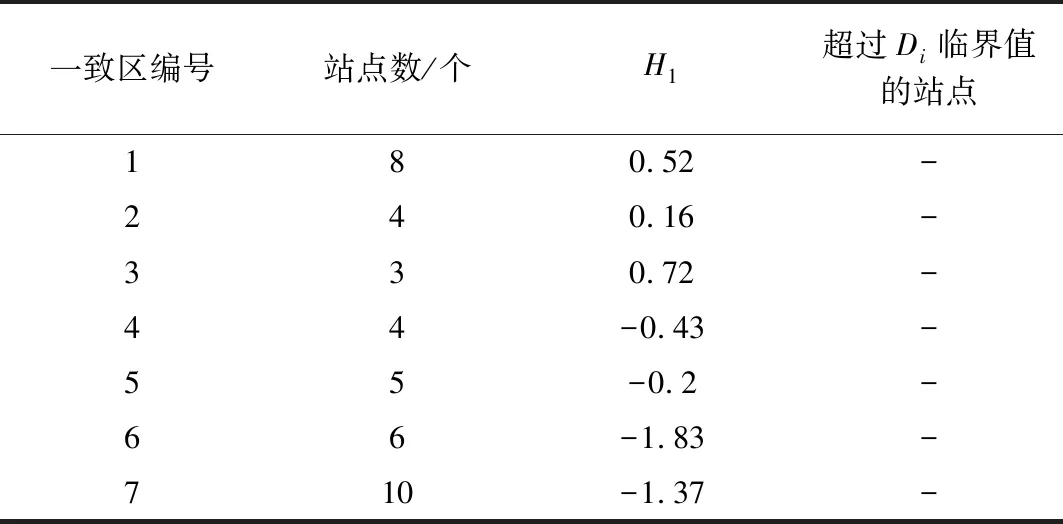
表1 一致区异质性和不和谐度检验结果

用Pearson相关系数r对可能存有相关性的区域内各站点进行检验，当|r|>0.7时认为站点资料存在相关性[12]。区域6内各站点均通过相关性检验，而区域7经过相关性检验后，宁化(58818)和清流(58819)，泰宁(58820)和建宁(58822)的相关系数均大于0.7。对于存在相关性的站点，要进行灵敏度检验，以判断是否舍弃，具体方法见下式：

(14)

式中，q0和q1指去除相关站点前后的地区无量纲百年一遇估计值，通过比较该站点资料对一致区内百年一遇的降雨频率估计值的影响程度来进行舍弃，当REq>5%时考虑剔除该站点。区域7的灵敏度检验结果如表2所示，REq均小于5%，相关站点均通过检验，全部保留。最终水口流域的分区结果见图3，整个研究区域分为7个一致区，其中区域2、区域4属于水口流域以外的缓冲区域。

表2 区域7灵敏度检验结果

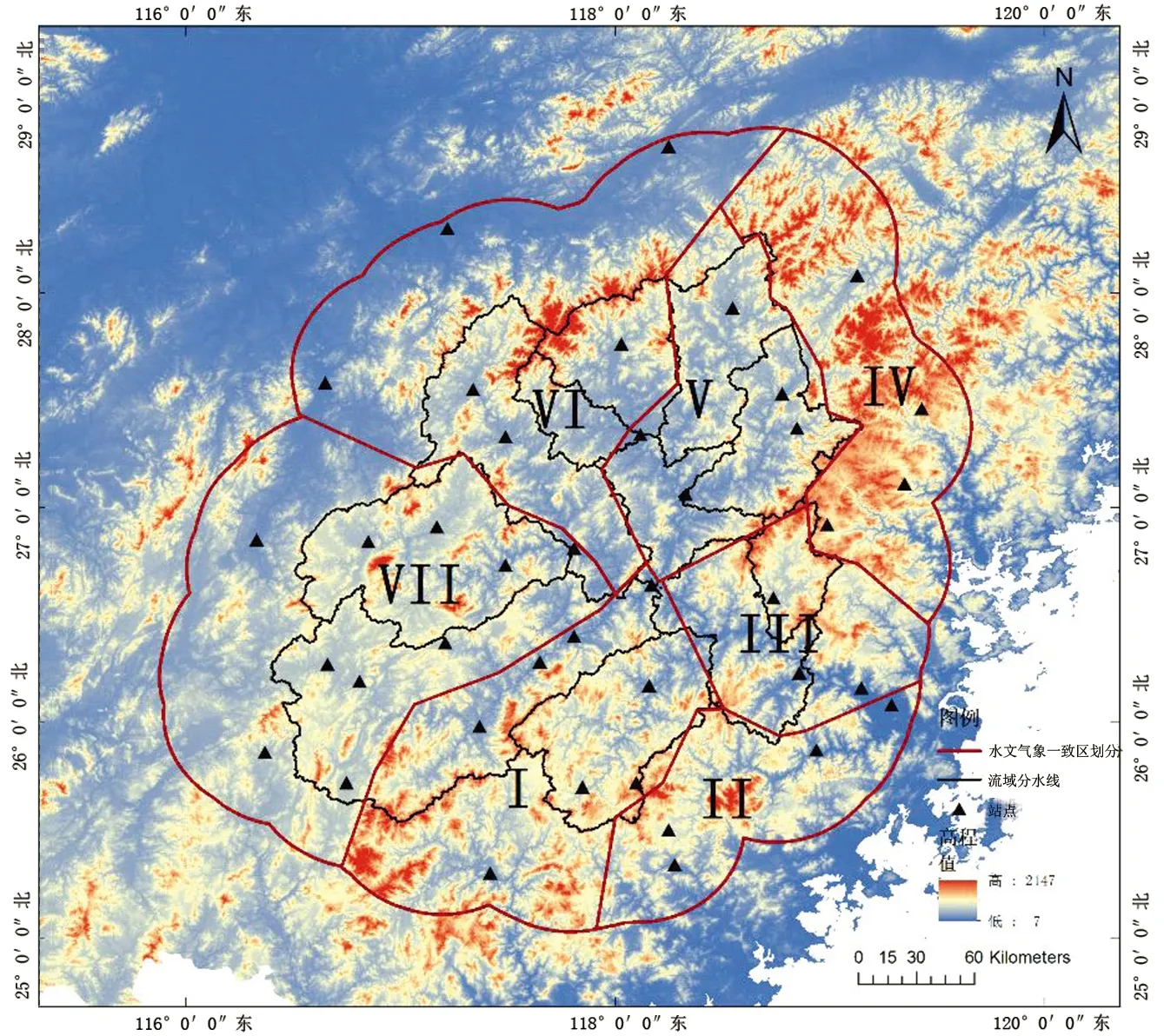
图3 水口流域水文气象一致区划分图

3.2 线型选择和频率分析

在一致区的基础上对各区进行拟合优度检测，具体结果见表3。以区域2为例，在蒙特卡洛模拟检测中只有GPA和PE3符合|ZDIST|≤1.64。在均方根误差检测中GPA线型的RMSE最小，为0.021，说明其GPA分布线型的相对较好。在实测数据检测中GPA线型的RE评分为20.5，评分最高，说明拟合效果在五种候选线型中为最好。综合以上考虑区域2的最优分布线型为GPA。其余各一致区也采用类似分析，最终最优线型选择结果为第2、4区为GPA，第5区为GNO，其余各区为GEV。

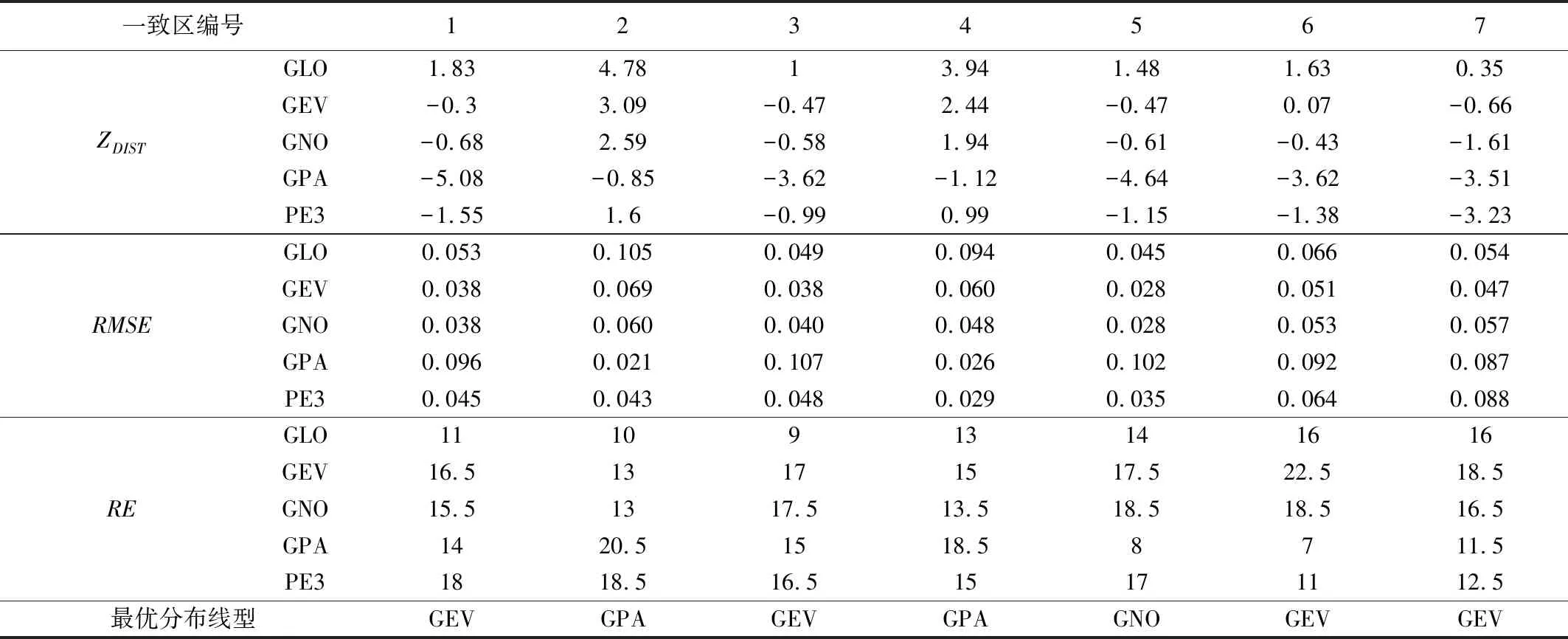
表3 各一致区拟合优度检测结果

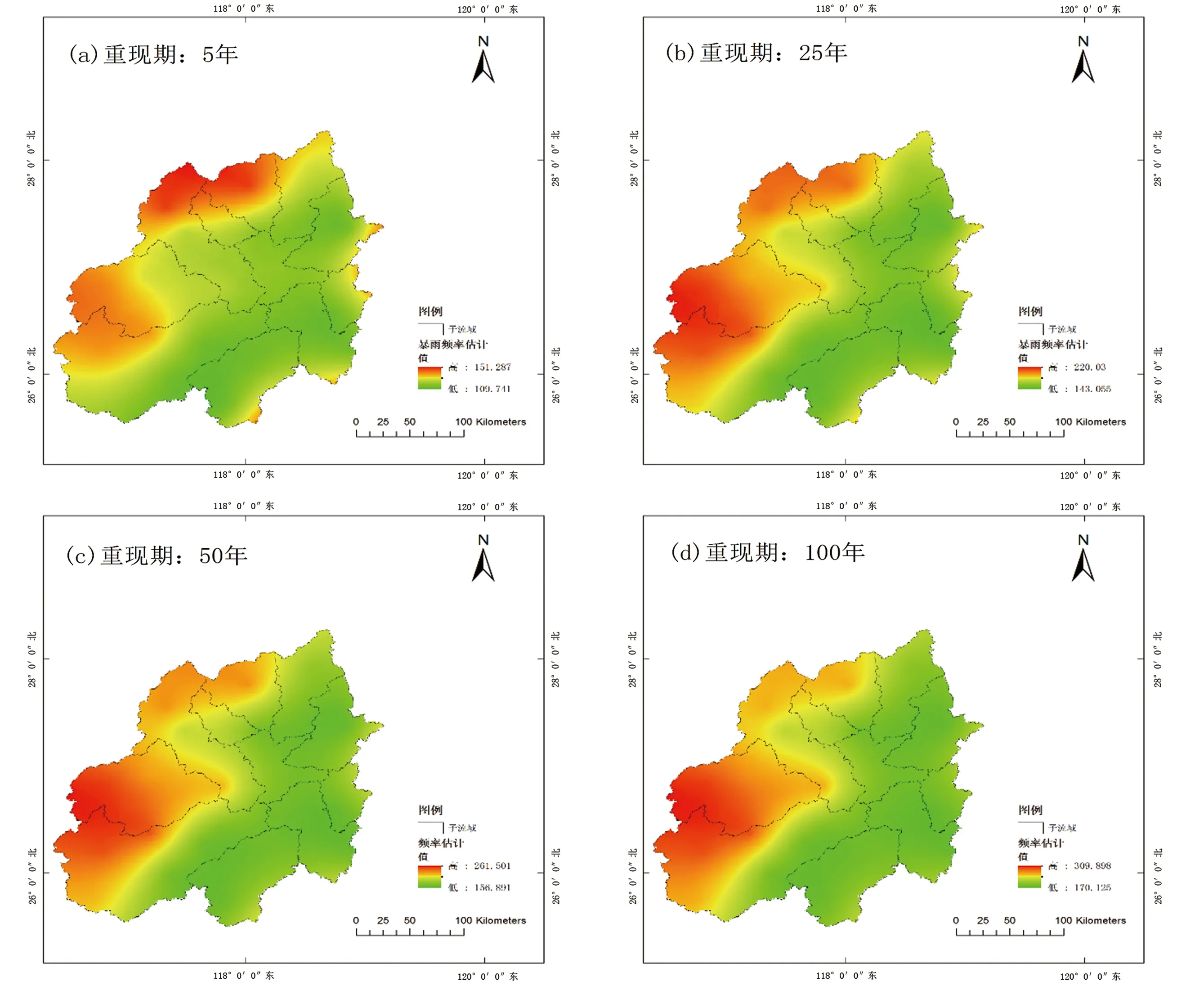
图4 不同重现期下空间频率分布图

基于各一致区的最优分布线型计算出地区分量并与区域内的本地分量结合，最终得到各雨量站不同重现期下的暴雨频率估计值。以5、10、50、100年重现期为例，将各站的频率估计值经过空间插值得到相应重现期下的频率分布图(图4)。从图中可以看到，当重现期为5年一遇时，频率估计值空间分布呈现北高南低趋势，大致区在第6一致区内的富屯溪、麻阳溪、崇阳溪流域。重现期为10年一遇时，水口流域的频率估计值有西北向东南逐渐递减，大值区分为两部分，除了与5年一遇的大值区重合外还有一部分位于第7一致区内的金溪、沙溪流域。随着重现期增加，流域的频率估计值空间分布呈现西高东低趋势，大值区位于第7一致区内的金溪、沙溪流域交界处。结合流域地形图发现，地势较高的山区的频率设计值大于平原地区。重现期为5年时流域的频率估计值在109.741～151.287mm。当重现期增加到100年时，流域的频率估计值在170.125～309.898mm。可以看出，随着重现期的递增，频率设计值的范围也在逐渐增大。

4 结论

本文基于地区线性矩法结合水口流域内及周边雨量站历史年最大日降雨资料，探究不同重现期下水口流域的暴雨频率估计值。分析发现，研究区域内可划分为7个水文气象一致区，其中水口流域内可分为5个一致区。通过频率分布线型拟合优度检测，第1～第7一致区的最优分布线型分别为GEV、GPA、GEV、GPA、GNO、GEV、GEV。通过计算不同重现期下的频率估计值发现，随着重现期的增加，频率估计值的范围也在增加。频率大值区多数集中在第6、第7一致区内，且山区的频率设计值大于地势低平的地区。

地区线性矩法是一种较新的频率计算方法，本研究结果可对水口电站流域内的防洪防汛规划工作提供参考。在现实中，降水并不是形成洪涝灾害的唯一因素，还需考虑到地形、社会经济等因素，未来可在本文研究结果的基础上，与上述因素结合形成暴雨风险区划，为防汛工作提供有力支撑，这也是下一步研究的方向。