具有对数型衰减初值的半线性波动方程解的爆破

蔡春玲, 黄守军

(安徽师范大学数学与统计学院,安徽芜湖 241002)

1 引言

本文主要研究如下低维空间中半线性波动方程的柯西问题

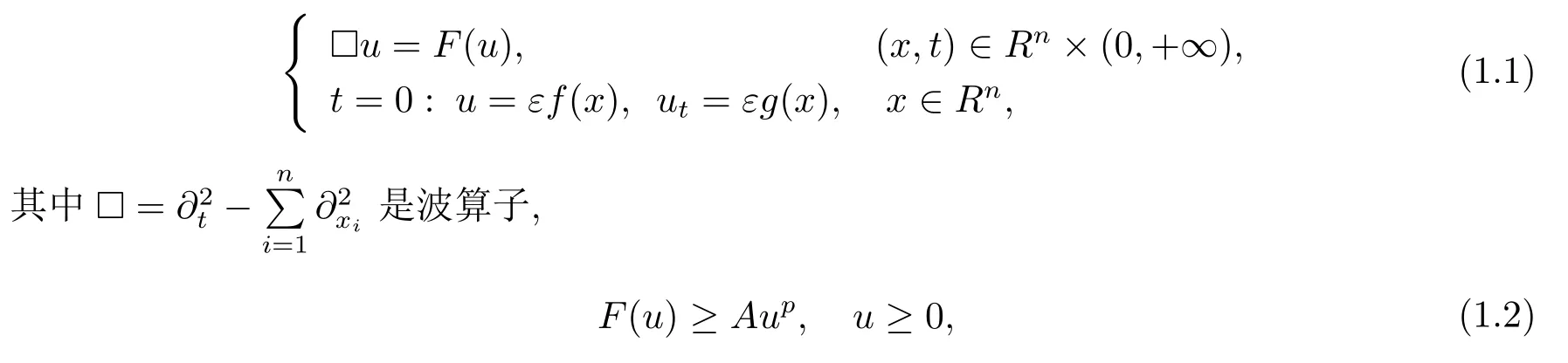
A>0,p>1,ε>0 是小参数.考虑n=2 和n=3 情形, 且p>p0(n), 其中p0(n) 是下列二次方程的正根

对于半线性波动方程柯西问题(1.1), 已经有了很多关于解整体存在和爆破的相关结果.当初值f(x),g(x) 具有紧支集且F(u) =|u|p时, 柯西问题(1.1) 有Strauss 猜想.即: 初值“充分小”,p>p0(n), 则式(1.1) 有整体解; 初值在某种意义下为正, 且1

对于n=3 情形, John[1,2]得到如下结果: 设F(u) 满足

对于临界情形p=p0(3) 和p=p0(2), Schaeffer[5]已经证明了即使对于小初值, 式(1.1)不存在整体解.

至此, 对于n=2 和n=3 的情形, Strauss 猜想已经得到完整验证.

对于高维情形n ≥4, 次临界情形1p0(n) 被Georgive, Lindblad 和 Sogge[7]证明.而临界情形p=p0(n) (n ≥4) 被Yordanov 和Zhang[8]以及Zhou[9]分别独立验证, 并且对于情形n ≥2, Zhou 和Han[10]给出了临界情形p=p0(n) 解的生命跨度的上界估计, 有关最新结果也可参见Rammaha,Takamura, Uesaka 和Wakasa[11].

若初值不具有紧支集, 则式(1.1) 解的情况会发生变化.事实上, 对于n= 3 情形,Asakura[12]设F(u) 满足式(1.3), 且p>p0(3), 初值f(x)∈C3(R3),g(x)∈C2(R3).如果初值满足

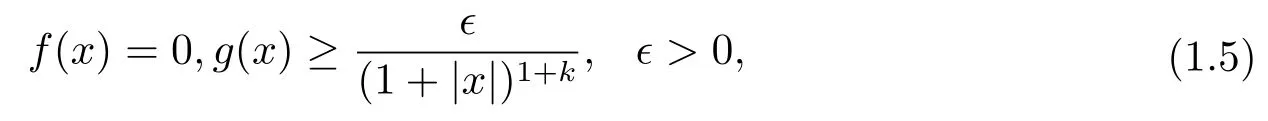
最近, Kong 和Liu[15]提出双曲Yamabe 问题, 考虑(1+n) 维 Minkowski 空间中的Yamabe 方程解的整体存在与爆破.Minkowski 时空中的双曲Yamabe 问题为如下半线性波动方程柯西问题所刻画

在文 [15]中, Kong 和 Liu 证明: 若初值f(x)∈C3(Rn),g(x)∈C2(Rn)(n=2 或 3), 且满足

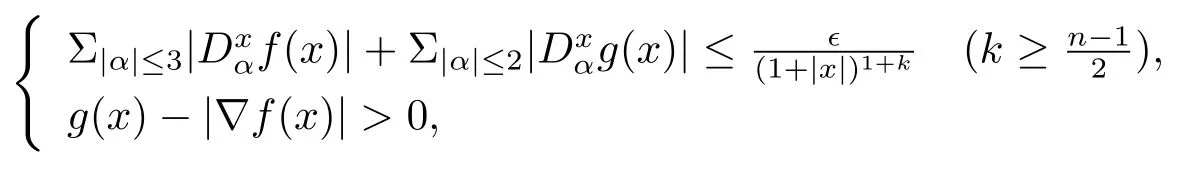
则柯西问题(1.6) 的光滑解整体存在; 若初值f(x)∈C3(Rn),g(x)∈C2(Rn) (n=2 或3), 且满足

本文研究一类具有衰减初值的半线性波动方程的柯西问题(1.1).不同于Asakura[12]和Kong 和Liu[15], 假设初值是具有形如式(2.1) 的对数型的衰减, 比代数衰减更缓慢一些.得到了半线性方程的柯西问题(1.1) 的解在有限的时间内爆破, 并得到了生命区间的下界.

2 主要结果

下面给出本文主要结果.

定理2.1设f(x)∈C3(Rn),g(x)∈C2(Rn)(n=2 或3).若初值满足如下条件

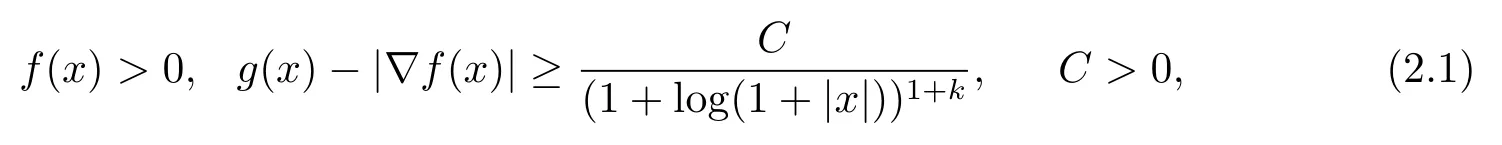
这里C0是与ε无关的正常数.

定理2.1 中解的正性可由引理3.3 保证.由定理2.1, 可得Yamabe 问题(1.6) 的结论.

推论 2.1对于n=2 和n=3 情形的 Yamabe 问题 (1.6).设f(x)∈C3(Rn),g(x)∈C2(Rn) 且满足式(2.1),则柯西问题(1.6)的解存在区间为[0,T∗), 生命跨度T∗的下界由式(2.2) 给出.

注2.1Kong 和Liu[15]未明确给出Yamabe 问题(1.6) 解的生命跨度的估计.

注2.2对于F(u) 满足式(1.3), 初值满足式(1.5), 且Tsutaya[13]指出柯西问题(1.1) 的解必发生爆破, 并给出同样的下界估计式(2.2).由此, 初值的对数型衰减虽比代数型衰减慢, 但不影响生命跨度的下界估计.

注 2.3在文献[13]中, Tsutaya 设F(u) =A|u|p,A> 0.若初值满足f(x) = 0,则生命跨度T∗满足其中c0为与C无关的正常数.因此, 猜测柯西问题(1.1) 的生命跨度T∗也满足其中c1为与ε无关的正常数.

3 主要结果的证明

在这一节中, 将给出一些引理以及定理2.1 的证明.尽管所需引理在Kong 和Liu[15]和Kubota[16]中已经给出, 但是为了完整起见, 在此依然将其列出, 证明可参见Kong 和Liu[15]和Kubota[16].

引理3.1考虑下列柯西问题

其中n=2 或3.当f(x)∈C3(Rn),g(x)∈C2(Rn),w(t,x)∈C2(Rn), 有

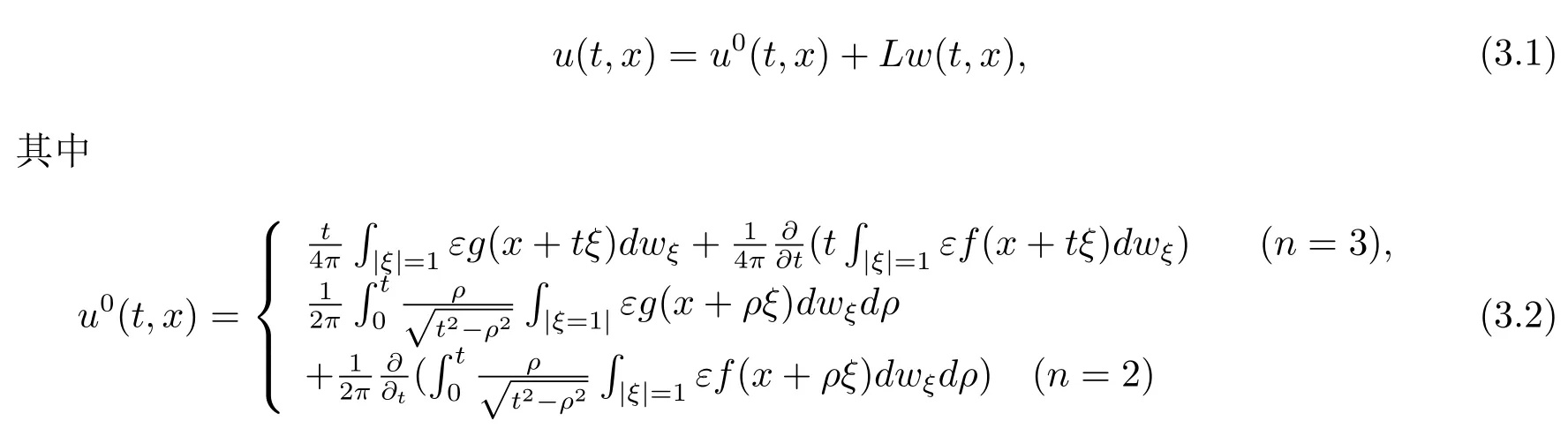
是柯西问题

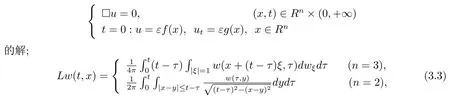
是柯西问题

的解.

引理 3.2若b(λ) 是 (−∞,∞) 上连续函数, 则

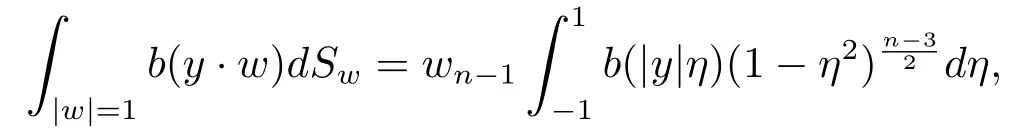
引理3.3若f(x)∈C3(Rn),g(x)∈C2(Rn) 满足式(2.1), 则当ε充分小时, 柯西问题(1.1) 在[0,+∞) 上有正的C2解.

证明参见Kong 和Liu[15], 此处从略.

定理2.1 的证明利用John[1]和Kong 和Liu[15]中的迭代法来证明.由引理3.3 知, 只要u存在, 则u>0.当n=3 时, 由式 (3.2) 和 (2.1) 有

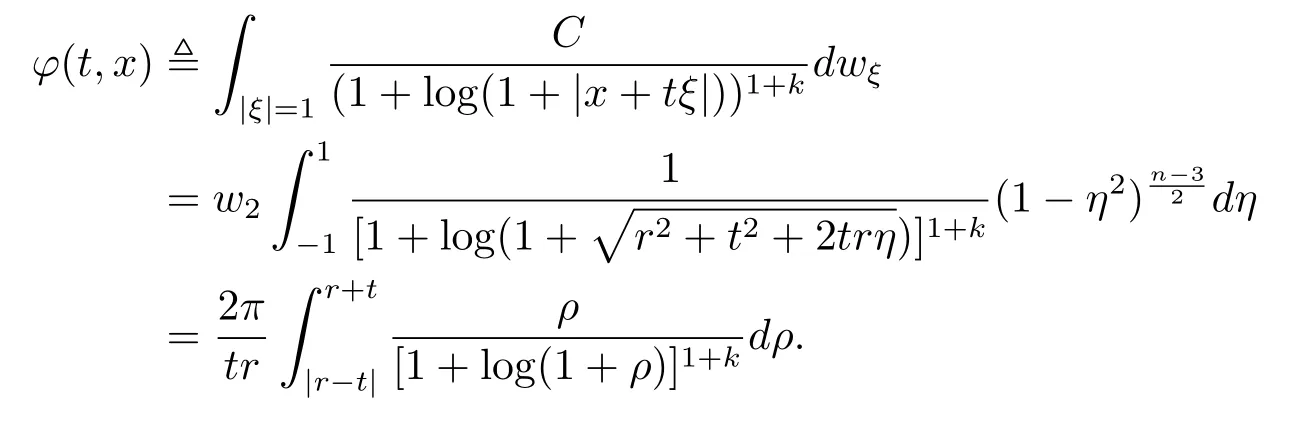
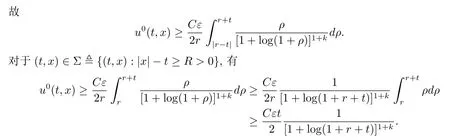
若函数p(t,x) 是 Cm(m ≥2) 光滑的, 记为p(t,x) 在半径为r的球面上的平均值, 即由式 (3.3) 得

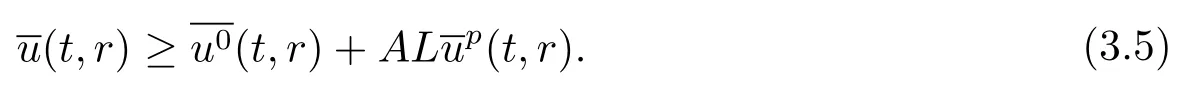
又由u>0, 成立

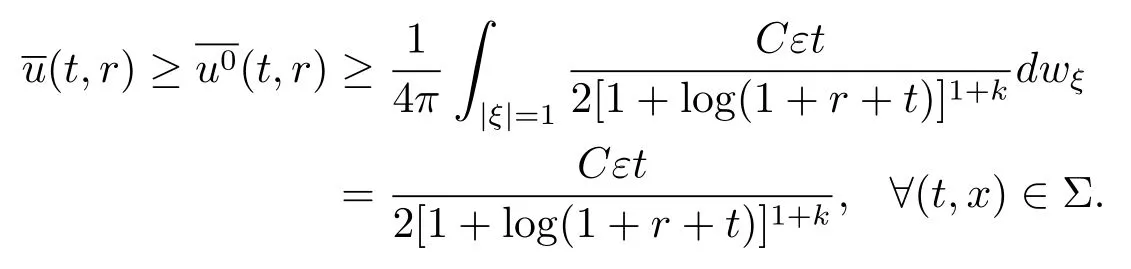
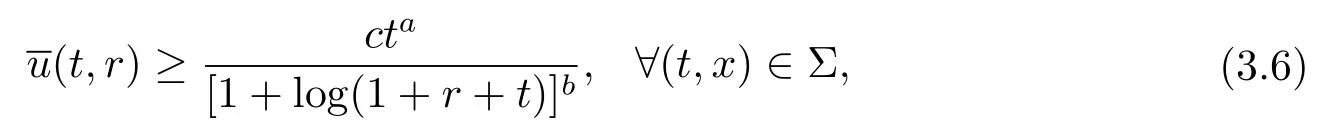
其中a,b,c均为正常数.显然当式 (3.6) 是满足的.由式 (3.5)–(3.6),

一直迭代下去, 并比较式(3.6) 和(3.7), 可定义如下序列{aj},{bj},{cj},

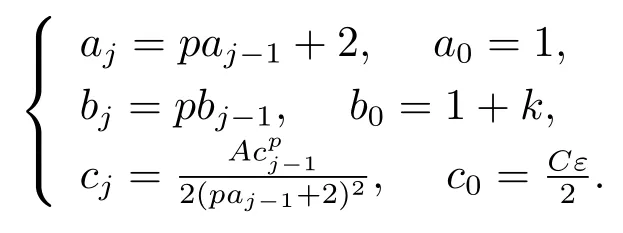
从而有

和

因此可以得到

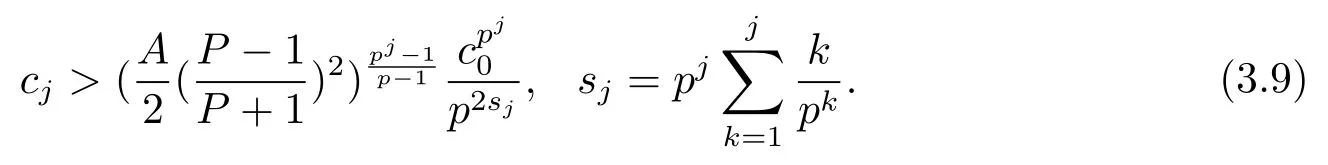
联立式(3.6), (3.8) 和(3.9) 得到其中

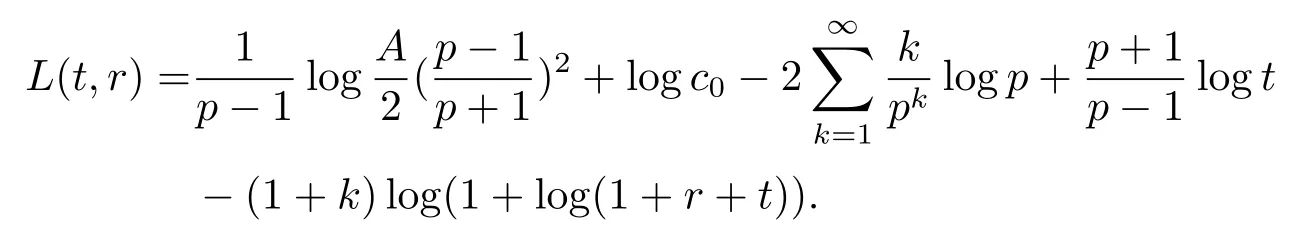
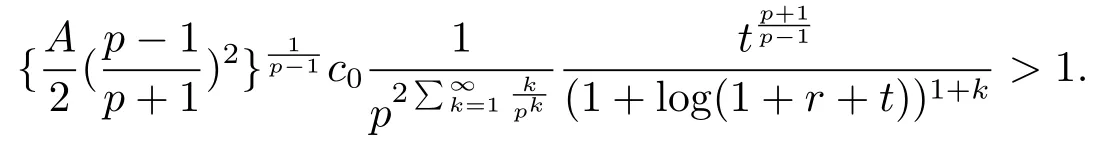
固定p, 从而有

当n=2 时, 由式 (2.1) 和 (3.2) 有

类似地, 设u有下列形式的估计

其中a,b,c均为正常数.显然当时, 式 (3.12) 是满足的.由式 (3.4)和(3.12), 可知

一直迭代下去, 并比较式(3.12) 和(3.13), 可定义如下序列{aj},{bj},{cj},

从而可求得

和

因此可以得到

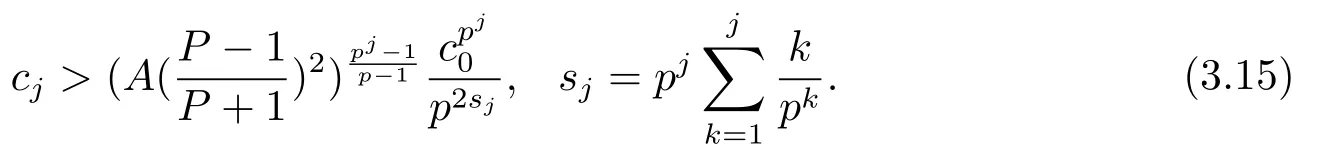
联立式(3.12), (3.14) 和(3.15), 可得

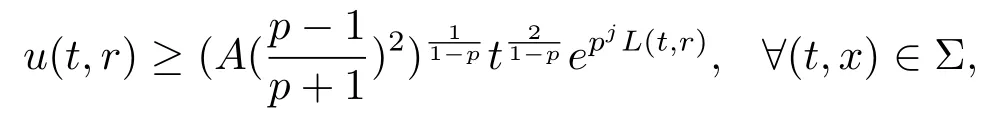
其中

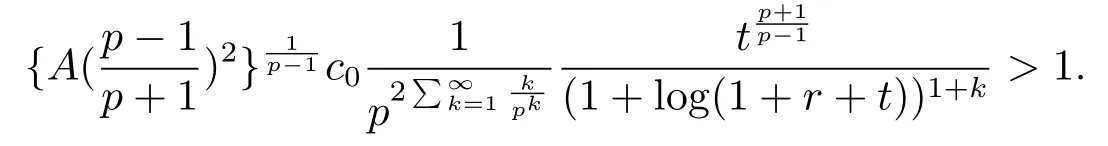
固定p, 从而有

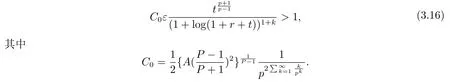
从而由式(3.16) 可得n=2 情形下生命区间的下界估计

因此柯西问题(1.1) 的解不会整体存在, 解的生命跨度由式(3.11) 和(3.17) 给出.证毕.