2019年美国数学竞赛(AMC12B)的试题与解答

华南师范大学数学科学学院(510631) 李湖南

这是今年美国数学竞赛(高三年级)在中国统一使用的考试B 卷.

1.Alicia had two containers.The first wasfull of water and the second was empty.She poured all the water from the first container into the second container，at which point the second container wasfull of water.What is the ratio of the volume of the smaller container to the volume of the larger container?

译文艾丽西娅有两个容器.第一个装满了的水，第二个是空的.她把第一个容器里的水全部倒进第二个容器里，这时第二个容器里充满了的水.问小容器与大容器的容积之比是多少？

解设第一、二个容器的容积分别为V1和V2，依题意有故(D)正确.

2.Consider the statement，“Ⅰfnis not prime，thenn-2 is prime.”Which of the following values ofnis a counterexample to this statement?

(A)11 (B)15 (C)19 (D)21 (E)27

译文考虑陈述“若n不是素数，则n-2 是素数.”以下哪个值n是这个陈述的一个反例？

解反例是指符合命题的条件但不符合命题的结论的例子，即满足“若n不是素数，则n-2 不是素数.”选项中只有27 满足，故(E)正确.

3.Which one of the following rigid transformations(isometries)maps the line segmentonto the line segmentA′B′so that the image ofA(-2,1)isA′(2,-1)and the image ofB(-1,4)isB′(1,-4)?

(A)reflection in the-axis

(B)counterclockwise rotation around the origin by 90°

(C)translation by 3 units to the right and 5 units down

(D)reflection in the-axis

(E)clockwise rotation about the origin by 180°

译文以下哪个刚体变换(等距变换)将线段映成线段使得点A(-2,1)对应A′(2,-1)且点B(-1,4)对应B′(1,-4)?

解由于点A(-2,1)和A′(2,-1)的两个坐标均互为相反数，可知原点O为线段AA′的中点，同理O也为线段BB′的中点.因此，将线段绕原点O顺时针旋转180°可得到，故(E)正确.

4.A positive integernsatisfies the equation (n+ 1)! +(n+2)!=440·n!.What is the sum of the digits ofn?

(A)2 (B)5 (C)10 (D)12 (E)15

译文正整数n满足方程(n+1)!+(n+2)!=440·n!，则n的各位数字之和是多少？

解原方程等价于(n+1)+(n+1)(n+2)=440，解得n=19，故(C)正确.

5.Each piece of candy in a shop costs a whole number of cents.Casper has exactly enough money to buy either 12 pieces of red candy，14 pieces of green candy，15 pieces of blue candy，ornpieces of purple candy.A piece of purple candy costs 20 cents.What is the least possible value ofn?

(A)18 (B)21 (C)24 (D)25 (E)28

译文商店里的每一块糖果的价格都是整数美分.卡斯帕刚好够钱买12 块红糖，或14 块绿糖，或15 块蓝糖，或n块紫糖.1 块紫糖值20 美分.问n的最小可能值是多少？

解最小公倍数[12,14,15]= 420，卡斯帕的钱一定是420 美分的整数倍，因此最小值n= 420/20=21，故(B)正确.

6.Ⅰn a given plane，pointsAandBare 10 units apart.How many pointsCare there in the plane such that the perimeter of∆ABCis 50 units and the area of ∆ABCis 100 square units?

(A)0 (B)2 (C)4 (D)8 (E)infinitely many

译文在一个给定的平面上，点A,B相距10 个单位，有多少个点C使得∆ABC的周长是50 个单位且面积是100个平方单位？

解不妨设A(0,0),B(10,0),由于∆ABC的面积为100，则点C到AB的高为20，可设C(x,20)，此时，∆ABC的周长为10+20+20=50，因此符合条件的点C不存在，故(A)正确.

7.What is the sum of all real numbersxfor which the median of the numbers 4,6,8,17,andxis equal to the mean of those five numbers?

译文所有使得五个数4,6,8,17 和x的中位数和平均数相等的实数x之和是多少？

解中位数只可能是6,8 或x： (1)若中位数是6，则解得x=-5;(2)若中位数是8，则解得x= 5，不符合要求; (3)若中位数是x，则解得也不符合要求.故(A)正确.

8.Letf(x)=x2(1-x)2.What is the value of the sum

译文设f(x)=x2(1-x)2，则下列式子的值是多少？

因此所求式子为0，故(A)正确.

9.For how many integral values ofxcan a triangle of positive area be formed having side lengths log2x,log4x,3?once.(Paula is allowed to visit a city more than once.)How many different routes can Paula take?

(A)0 (B)1 (C)2 (D)3 (E)4

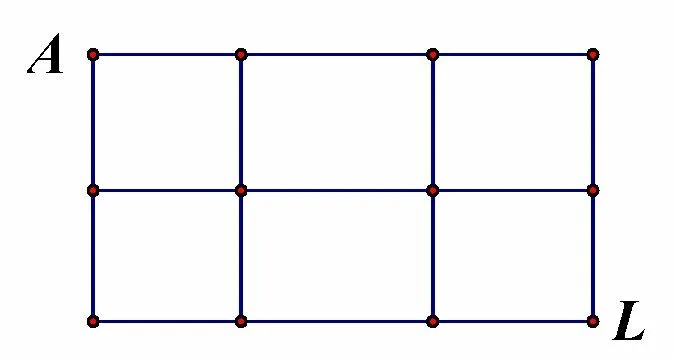
图1

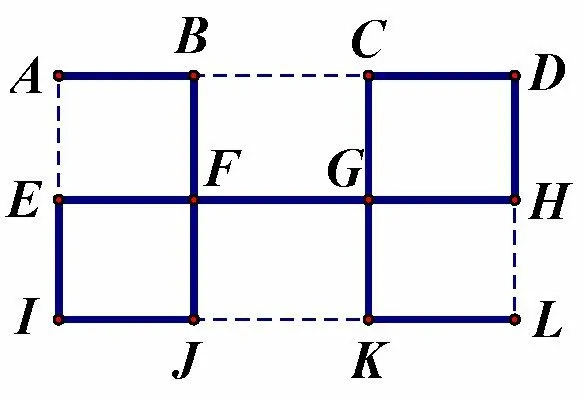
图2

译文图1给出了12 个城市和连接两个城市之间的17条路段.保罗想从城市A出发，不重复地走过13 条路段，到达城市L(允许保罗经过同一个城市多次).问保罗有多少条路可以选择？

解如图2所示，点A,D,I,L的度数均为2，点B,C,E,H,J,K的度数均为3，点F,G的度数均为4.由于不走重复路段，所以除了出发城市和到达城市的度数是奇数之外，其它经过城市的度数必须是偶数.又要求走过13 条路段，即有4 条路段不需走过，度数和要减少8，可 知 点A,B,C,E,H,J,K,L的 度 数 均 需 减 少1，而 点D,F,G,I的度数均保持不变.因此，去掉的路段只能是AE,BC,JK,HL.所以保罗选择的路为

每个圈均有顺时针和逆时针两种方式，故共有4 种选择，(E)正确.

11.How many unordered pairs of edges of a given cube determine a plane?

(A)57 (B)59 (C)61 (D)62 (E)63

译文有多少个整数x使得以log2x,log4x,3 为边长可以构成一个三角形？

解由于log2x ≥log4x，当x为 正 整数时.以log2x,log4x,3 为边长可以构成一个三角形，从而只要满足解得4＜x ＜64，即满足条件的x共有59 个，故(B)正确.

10.The figure below is a map showing 12 cities and 17 roads connecting certain pairs of cities.Paula wishes to travel along exactly 13 of those roads，starting at cityAand ending at cityL，without traveling along any portion of a road more than

(A)12 (B)28 (C)36 (D)42 (E)66

译文在一个立方体中，有多少对无序的边决定一个平面?

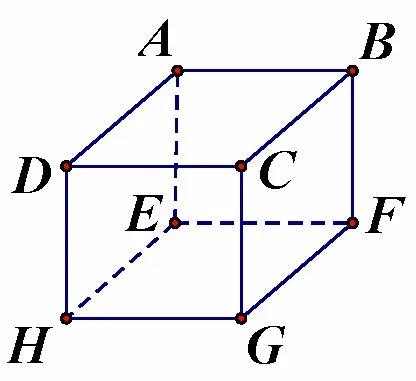
图3

解如图3所示，ABCD -EFGH是一个立方体，对于任意一条边，不妨设为AB，可以与AB构成一个平面的边有BC,CD,AD,AE,BF,EF,HG，共7 条.因此所求数目为对，故(D)正确.

12.Right triangleACDwith right angle atCis constructed outwards on the hypotenuseof isosceles right triangleABCwith leg length 1，as shown，so that the two triangles have equal perimeters.What is sin(2∠BAD)?

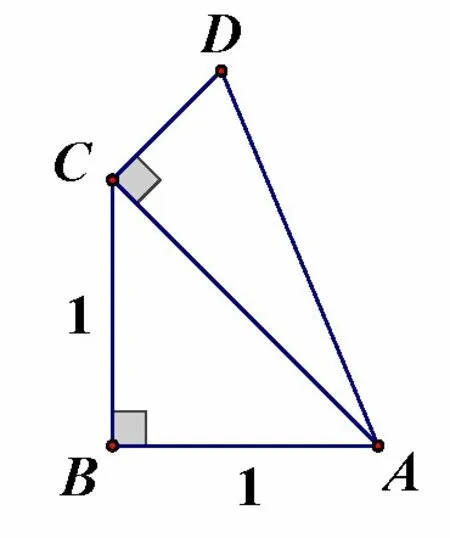
图4

译文如图4所示，ABC是一个腰长为1 的等腰直角三角形，在斜边上建立直角三角形ACD，∠ACD为直角，使得两个三角形周长相等.求sin(2∠BAD)的值是多少?

解依题意，∠CAB= 45°,设CD=x，则由于周长相等，从而CD+AD=解得于是进而于是有

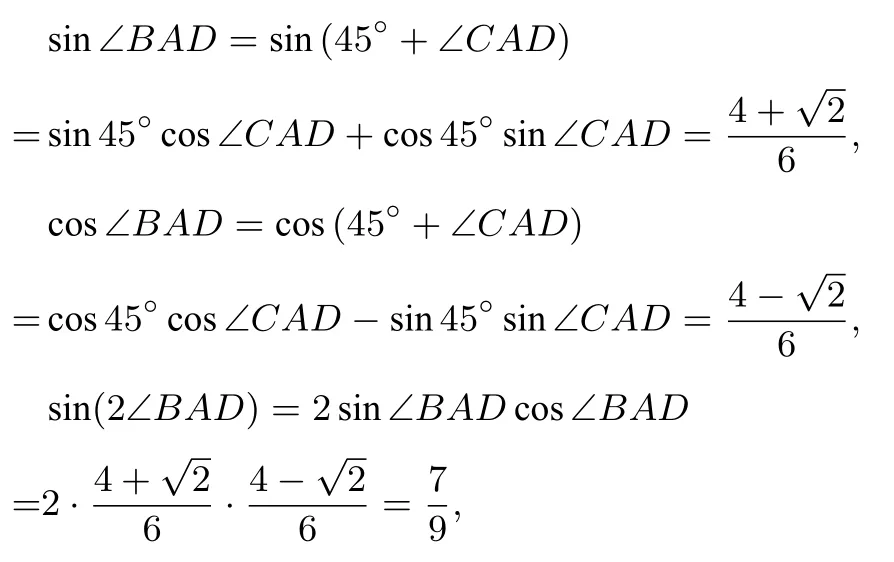
故(D)正确.

13.A red ball and a green ball are randomly and independently tossed into bins numbered with the positive integers so that for each ball，the probability that it is tossed into binkis 2-kfork=1,2,3,··· ,What is the probability that the red ball is tossed into a higher-numbered bin than the green ball?

译文一个红球和一个绿球被随机地、独立地抛入用正整数编号的箱子中，每个球被抛入箱子k的概率为2-k，其中k=1,2,3···.则红球被抛入比绿球编号更高的箱子的概率是多少?

解红球被抛入比绿球编号更高的箱子的概率与绿球被抛入比红球编号更高的箱子的概率是相等的，而红球与绿球被抛入同一个箱子的概率是结果为因此所求概率为故(C)正确.

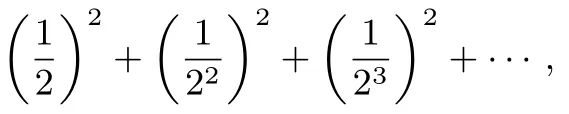
14.LetSbe the set of all positive integer divisors of 100，000.How many numbers are the product of two distinct elements ofS?

(A)98 (B)100 (C)117 (D)119 (E)121

译文设S是100，000 的所有正整数因子的集合，则S中两个不同元素的乘积共有多少个?

解100000 = 25×55，则S={2i×5j:i,j=0,1,2,3,4,5}，于是S中两个元素乘积的集合为{2i×5j:i,j=0,1,2,3,··· ,10}，共121 个数.注意到题目要求两个元素不同，所以乘积中要去掉1,210,510,210×510这四个数，剩下117 个，故(C)正确.

15.As showing in the figure，line segmentis trisected by pointsBandCso thatAB=BC=CD= 2.Three semicircles of radius 1，have their diameters onlie in the same halfplane determined by lineAD，and are tangent to lineEGatE,FandG，respectively.A circle of radius 2 has its center atF.The area of the region inside the circle but outside the three semicircles，shaded in the figure，can be expressed in the formwherea,b,canddare positive integers andaandbare relatively prime.What isa+b+c+d?

(A)13 (B)14 (C)15 (D)16 (E)17

图5

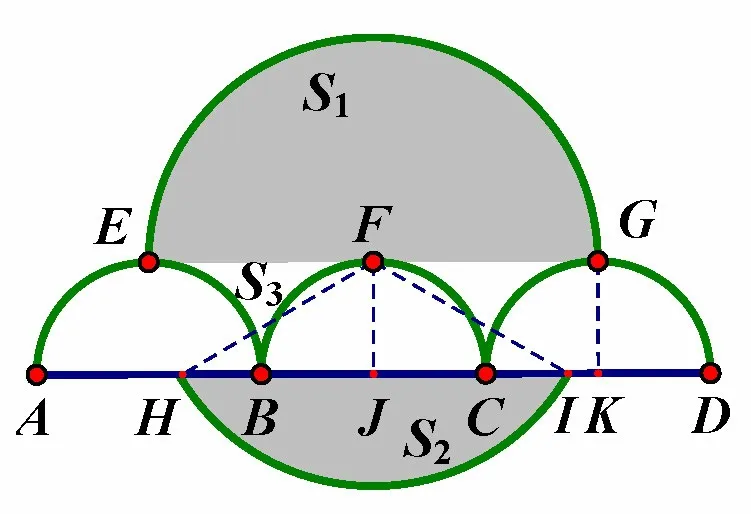
图6

译文如图5所示，线段被点B,C三等分，AB=BC=CD=2.三个半径为1 的半圆和的直径均在上，位于由直线AD确定的同一半平面上，且和直线EG分别相切于点E,F,G.另有一个以点F为圆心、半径为2 的圆，圆内而三个半圆外的区域被涂成了阴影部分，面积可以表示为其中a,b,c,d都是正整数且a,b互素.问a+b+c+d是多少?

解如图6所示，设⊙F与线段AD相交于点H,I，取线段BC,CD的中点分别为J,K，连结FH,FI,FJ,GK，则FJKG是个矩形，且FJ=GK= 1，从而∠IFJ= 60°，所求阴影部分的面积S=S1+S2+S3，其中S1为⊙F的上半圆，S2为⊙F被HI所截的弓形，S3为其余部分.于是，因此S=即有a=7,b=3,c=3,d=4，得a+b+c+d=17，故(E)正确.

16.There are lily pads in a row numbered 0 to 11，in that order.There are predators on lily pads 3 and 6，and a morsel of food on lily pad 10.Fiona the frog starts on pad 0，and from any given lily pad，has achance to hop to the next pad，and an equal chance to jump 2 pads.What is the probability that Fiona reaches pad 10 without landing on either pad 3 or pad 6?

译文有0 到11 号睡莲叶子按顺序排成一排，3 号和6号莲叶上有捕食动物，10 号莲叶上有一小块食物.青蛙菲奥纳在0 号莲叶上，从任意一片莲叶开始，它跳到下一片莲叶和跳到下两片莲叶的概率均为问菲奥纳不经过3 号和6号莲叶就到达10 号莲叶的概率是多少?

解菲奥纳不经过3 号和6 号莲叶，就必须从2 号跳到4 号，再跳到5 号，然后跳到7 号，这三步连跳的概率是菲奥纳从0 号跳到2 号有两种方法： 直接跳过去，或者先跳到1 号再跳到2 号，概率是菲奥纳从7 号跳到10 号有三种方法： 一步步跳过去，或者先跳到8 号再跳到10 号，或者先跳到9 号再跳到10 号，概率是因此所求概率为故(A)正确.

17.How many nonzero complex numberszhave the property that 0,zandz3，when represented by points in the complex plane，are the three distinct vertices of an equilateral triangle?

(A)0 (B)1 (C)2 (D)4 (E)infinitely many

译文有多少个非零复数z使得三个复数0,z,z3在复平面上表示的点恰好构成一个等边三角形?

解设z=r(cosθ+i sinθ)，其中r ＞0,0° ≤θ ＜360°，则z3=r3(cos 3θ+ i sin 3θ)，由于0,z,z3在复平面上表示的点构成正三角形，从而有k ∈ℕ，解得r= 1,θ= 30°,150°,210°,330°，所以符合条件的z有4 个，故(D)正确.

18.Square pyramidABCDEhas baseABCD，which measures 3 cm on a side，and altitudeperpendicular to the base，which measures 6 cm.PointPlies on，one third of the way fromBtoE;pointQlies on，one third of the way fromDtoE;and pointRlies on，two thirds of the way fromCtoE.What is the area，in square centimeters，of ∆PQR?

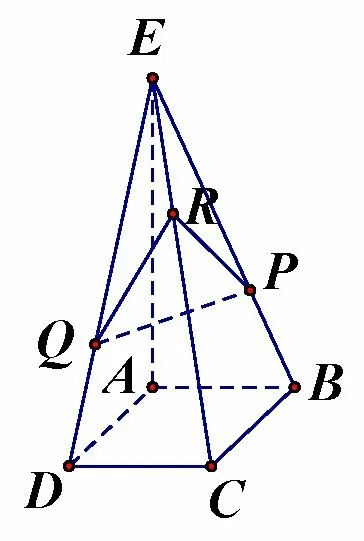
图7

译文ABCDE是一个正方棱锥，底面ABCD是一个边长为3 cm 的正方形，棱垂直于底面，长度为6 cm.点P是上从B到E的第一个三等分点;点Q是上从D到E的第一个三等分点;点R是上从C到E的第二个三等分点.则∆PQR的面积是多少平方厘米?

解如图7所示，建立空间直角坐标系，设A(0,0,0),B(0,3,0),C(3,3,0),D(3,0,0),E(0,0,6),则有P(0,2,2),Q(2,0,2),R(1,1,4),于是求得PR=同理有点R到PQ边上的高为从而所求面积为故(C)正确.

19.Raashan，Sylvia，and Ted play the following game.Each starts with$1.A bell rings every 15 seconds，at which time each of the players who currently has money simultaneously chooses one of the other two players independently and at random and gives$1 to that player.What is the probability that after the bell has rung 2019 times，each player will have$1? (For example，Raashan and Ted may each decide to give$1 to Sylvia，and Sylvia may decide to give her dollar to Ted，at which point Raashan will have$0，Sylvia will have$2，and Ted will have$1，and that is the end of the first round of play.Ⅰn the second round Raashan has no money to give，but Sylvia and Ted might choose each other to give their$1 to，and the holdings will be the same at the end of the second round.)

译文拉珊、西尔维娅和特德在玩下列游戏： 开始每人持有1 美元，铃每15 秒响一次，然后每个手上有钱的玩家同时独立、随机地选择另外两个玩家中的一个，并给该玩家1美元.请问铃响2019 次后，每个玩家仍然持有1 美元的可能性是多少? (例如，拉珊和特德各自决定给西尔维娅1 美元，西尔维娅决定给特德1 美元，第一轮游戏结束，此时拉珊将得到0 美元，西尔维娅将得到2 美元，特德得到1 美元，在第二轮中，拉珊没有钱可给，但西尔维娅和特德可能会选择给对方1 美元，那么第二轮结束时，他们的持有量将不变.)

解记拉珊、西尔维娅和特德分别持有的现金m,n,k美元为 (m,n,k)，则在任何时候都有 (m,n,k)∈ {(1,1,1),(2,1,0),(2,0,1),(1,2,0),(1,0,2),(0,1,2),(0,2,1)}.

(1)当(m,n,k)= (1,1,1)时，铃响之后，可能出现以下8 种情况：

此时的结果分别为(1,1,1),(1,1,1),(2,1,0),(1,2,0),(0,2,1),(0,1,2),(2,0,1),(1,0,2),即一轮过后结果仍然是(1,1,1)的概率为

(2)当三个人持有现金不一样的时候，不妨设(m,n,k)=(2,1,0)，铃响之后，可能出现以下4 种情况：

此时的结果分别为(2,1,0),(1,1,1),(2,0,1),(1,0,2)，即一轮过后结果是(1,1,1)的概率为： 因此，不管哪种情况，2019 轮过后，结果回到(1,1,1)的概率就是，故(B)正确.

20.PointsA(6,13)andB(12,11)lie on a circleωin the plane.Suppose that the tangent lines toωatAandBintersect at a point on thex-axis.What is the area ofω?

译 文A(6,13)和B(12,11)是平面上的一个圆ω上的两点.设ω上的过A和B两点的切线相交于x轴上的同一个点，则圆ω的面积是多少?

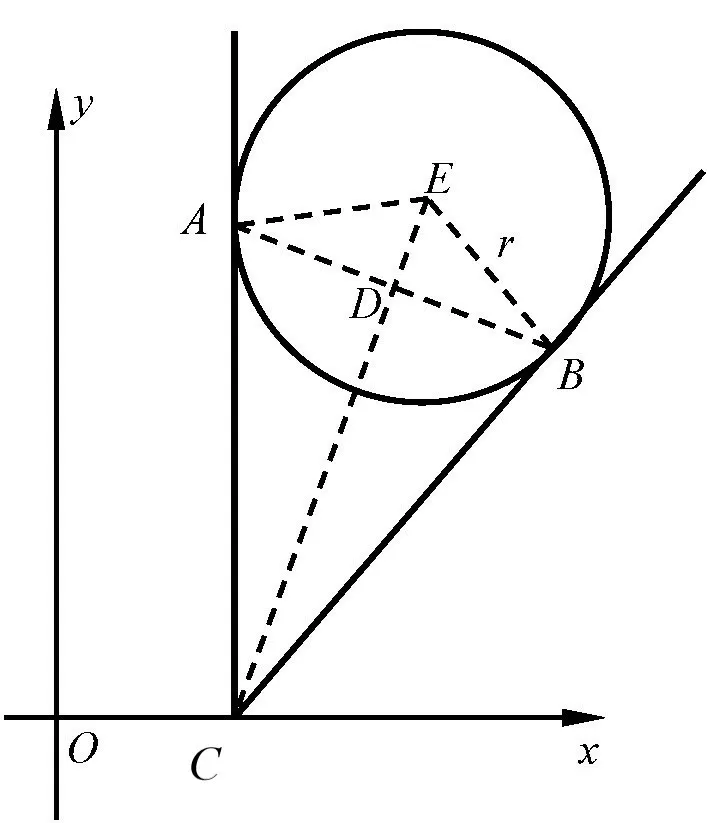
图8

解如图8所示，设圆ω的圆心为E，半径为r，两条切线交点为C，点C的坐标为(x,0)，连结EA,EB,EC,AB，且AB交EC于D，依题意有CA=CB,EA=EB，则点E,C均在AB的中垂线上，即EC ⊥AB，且有AC=DB，于是点D的坐标为(9,12)，另外,CB=解 得x= 5，即C的坐标为(5,0)，代入上式可得再 根据∆BCD∽ ∆CDB，可得有BE=因此，圆ω的面积为故(C)正确.

21.How many quadratic polynomials with real coefficients are there such that the set of roots equals the set of coefficients?(For clarification： Ⅰf the polynomial isax2+bx+0，and the roots arerands，then the requirement is that{a,b,c}={r,s}.)

(A)3 (B)4 (C)5 (D)6 (E)infinitely many

译文有多少个实系数二次多项式使得根的集合与系数的集合相等? (举例说明： 若多项式为ax2+bx+0，且根为r和s，则需要{a,b,c}={r,s}.)

解依题意，多项式ax2+bx+0 的系数中必出现相等的情况，分成以下四种：

(1)a=b=c，即a(x2+x+1)： 由于∆=-3a2＜0，从而多项式没有实根，不符合条件;

(2)a=b，即ax2+ax+c：两根为a,c，此时有a+c=-1,ac=解得两组解为或

(3)a=c，即ax2+bx+a：两根为a,b，此时有a+b=ab= 1，化简后可得a3+a+ 1 = 0，经图像分析可知该方程有唯一一组实数解;

(4)b=c，即ax2+bx+b：两根为a,b，此时有解得一组解为

综上可得，符合条件的二次多项式共有4 个，故(B)正确.

22.Define a sequence recursively byx0= 5 andfor all nonnegative integersn.Letmbe the least positive integer such thatⅠn which of the following intervals doesmlie?

(A)[9,26](B)[27,80](C)[81,242](D)[243,728](E)[729,∞)

译文定义递归数列如下：x0= 5,xn+1=,∀n ∈ℕ.令m是使得成立的最小正整数，则m在以下哪个区间?

由于x0＞4，可得xn+1＞4,∀n ∈ℕ; 又xn+1- xn=可得数列{xn}是单调下降的，则4＜xn ≤5，从而

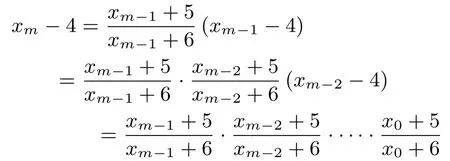
23.How many sequences of 0s and 1s of length 19 are there that begin with a 0，end with a 0，contain no two consecutive 0s，and contain no three consecutive 1s?

(A)55 (B)60 (C)65 (D)70 (E)75

译文有多少个长度为19 的只含0 和1 的序列： 以0 开头，以0 结尾，不包含两个连续的0，也不包含三个连续的1?

解0 后面只能接1 或11，记01 为A，011 为B，原问题就相当于将一些A和B排列在长度为18 的序列上，可能出现(1)6 个B： 只有1 种排列; (2)4 个B，3 个A： 共有种排列;(3)2 个B，6 个A： 共有种排列;(4)9 个A： 只有1 种排列.因此，符合条件的序列共有1+35+28+1=65 个，故(C)正确.

24.Letω=i.LetSdenote all points in the complex plane of the forma+bω+cω2，where0≤a ≤1,0≤b ≤1 and 0≤c ≤1.What is the area ofS?

译文设S表示复平面上所有形式为a+bω+cω2的点的集合，其中0≤a,b,c ≤1.问S的面积是多少?

解如图9所示，在复平面上，点A代表ω，点B代表ω2，则根据向量的加法，所有形式为bω+cω2,0≤b,c ≤1 的点集构成一个菱形AOBD及其内部.

再令点C代表1，则所有形式为a+bω+cω2,0≤a,b,c ≤1 的点集就是将菱形AOBD向右平移1 个单位，即得到正六边形AECFBD及其内部.因此所求面积为故(C)正确.

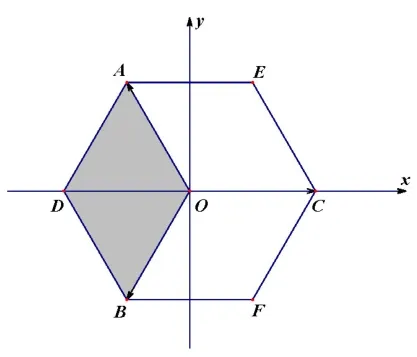
图9

25.LetABCDbe a convex quadrilateral withBC= 2 andCD= 6 .Suppose that the centroids of ∆ABC,∆BCDand ∆ACDform the vertices of an equilateral triangle.What is the maximum possible value of the area ofABCD?

译文设ABCD是一个凸四边形，BC= 2,CD= 6，若∆ABC,∆BCD,∆ACD的重心构成一个等边三角形，则ABCD的面积最大值是多少?

解如图10 所示，分别取BC,CD,AC的中点为E,F,G，连结AE,BG交于点O1，连结BF,DE交于点O2，连结AF,DG交于点O3，则 点O1,O2,O3分别为∆ABC,∆BCD,∆ACD的重心，由题意可得，∆O1O2O3是等边三角形.

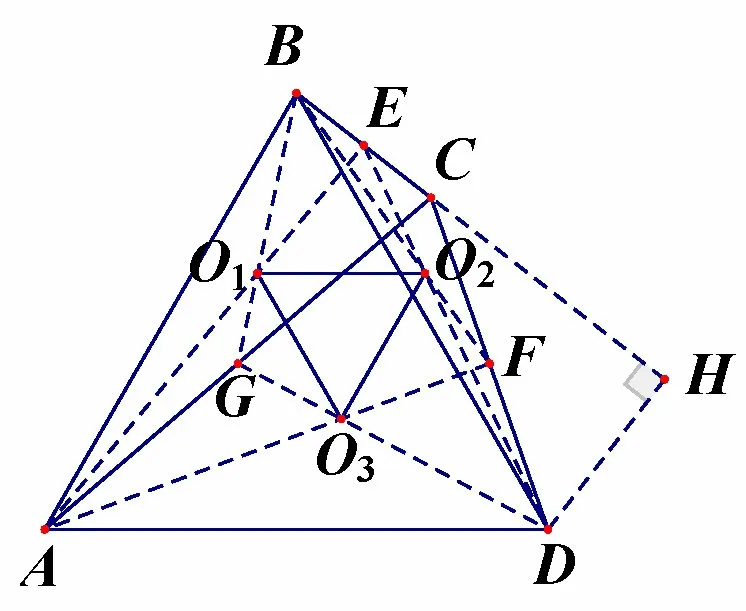
图10

另外，同 理2⇒O1O3‖ EF，而EF是∆BDC的中位线，即得EF ‖BD ⇒O1O3‖BD.因此，∆ABD也是等边三角形.则所求面积为SABCD=S∆ABD+S∆BCD=,过点D作BC的垂线，交BC的延长线于H，则有DH=CDsin ∠DCH=6 sin ∠BCD,CH=-6 cos ∠BCD,于 是BD2=BH2+DH2= (2-6 cos ∠BCD)2+(6 sin ∠BCD)2=40-24 cos ∠BCD,进而

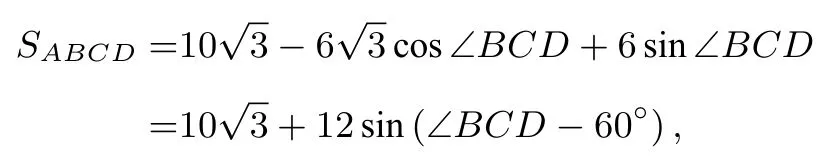
当∠BCD= 150°时，面积取最大值为故(C)正确.