土壤热通量板测量误差及Philip修正公式的适用性*

邢 洲，乔照钰，刘 刚

土壤热通量板测量误差及Philip修正公式的适用性*

邢 洲，乔照钰，刘 刚†

（中国农业大学资源与环境学院，北京 100193）

土壤热通量的测量是地表热量平衡研究中重要的一部分。测量土壤热通量有很多种方法，其中热通量板法简单易行但准确度无法判定。采用计算机模拟与室内实验相结合的方法，研究土壤热通量板测量误差及影响因素；将土壤作为均匀介质，将热通量板作为复合材料，研究复合材料在均匀介质中对温度场和热流分布的影响。此外，本文还对Philip在1961年提出的修正公式的效果进行了分析。结果表明，当土壤与热通量板的热导率接近时，热通量的测量误差较小；Philip修正公式在瞬态条件下的适用性较差。本研究表明，由于热通量板与土壤二者热导率的差异，热流在板边缘处会扭曲，从而导致热通量测量误差；由于Philip公式在推导过程中存在简化运算的处理，在土壤温度随时间波动的情况下，校正值与理论值间仍存在差异的现象，表明该公式的适用范围有限。

土壤热通量；热通量板法；土壤热导率

陆地与大气之间的物质与能量的交换，在全球气候变化与大气环流中有显著作用，并且也是各类生态研究中的重要研究内容[1]。地气之间能量交换的一个重要约束条件为地表热量平衡。地表热量平衡公式为：

式中，R为净辐射通量，W·m–2，是总收入辐射通量与总支出辐射通量的差值；为感热通量，W·m–2，是物体在加热或冷却过程中，温度升高或降低而不改变其原有相态所需吸收或放出的热量；LE为潜热通量，W·m–2，是物质发生相变，且温度不发生变化时吸收或放出的热量；0为地表热通量，W·m–2，反映了地面与下层土壤之间的热交换，是引起地表温度变化的热通量[2]。现有相关文献对地表热量平衡的研究多以净辐射通量、感热通量和潜热通量为主。虽然地表热通量与其他三项通量相比数值很小，但是它是瞬时能量平衡的重要贡献者[3]。地表热通量受到地表覆盖类型、土壤含水量状况以及太阳辐射等因素的影响而变化，不同情况下地表热通量在地表热平衡中所占比例不同[4-5]。地表热通量作为地表能量平衡的重要组成之一，是众多学科领域的一项重要参数。

通常通过测量土壤某一深度处的土壤热通量数值，可得到地表热通量。土壤热通量的准确测量在农业、气象、生态、地理与土木工程等领域均有重要的研究意义[6-7]。目前，获取土壤热通量的主要方法有量热法、梯度法、组合法和热通量板法。其中，热通量板在测量过程中存在接触热阻造成的误差：当将热通量板放入某一介质中或表面时，由于二者材料不同，即热特性上的差异，使得热通量板的存在增大或减少该介质本身的热阻，导致土壤热通量的测量值与真实值产生偏差[8]。针对这一问题，Philip[9]在1961年基于稳态热传导理论，提出了修正参数的概念。

通过分析常用土壤热通量测定方法的准确度，以及测量过程中可能导致误差的主要因素，可以帮助规范和改进测量技术，从而提高土壤热通量的测量精度，推进农、林、业、气象、生态等学科相关研究的顺利进行。本文以热通量板法为研究对象，模拟研究热通量板测量精度的影响因素，并且检验Philip在1961年提出的修正公式的适用性。

1 材料与方法

1.1 热通量板的相关原理

Carslaw和Jaeger在1959年推导出不同定解的条件下，一维坐标系下不同位置m）处温度（K）和热通量G（W·m–2）随时间变化的解析解。对于已知热特性参数的半无限长固体介质，初始温度为0 K，在端点处施加恒定热流0（W·m–2），即定解的条件设为：

这种情况下，不同位置处温度和热通量随时间的变化分别为：

式中，为热扩散系数，m2·s–1；（）为余误差函数。在室内实验设计中，可以通过满足定解条件式（1）～式（2）来实现，应用式（1）～式（4）作为热通量的理论参考值。

在实际测量中，通常将热通量板水平埋设在地表以下2.5～10 cm范围内[10]。当有热流穿过热通量板，板内的填充材料充当热阻，使板的上下表面产生温度差，创造一个热表面和一个冷表面，板内上下表面的热敏电阻感受温度，通过热电偶将温度差转换为电压差输出，通过下面公式计算出热通量：

式中，G为热通量，W·m–2；V为输出电压，V；E为热通量板参数，mV·m2·W–1。

由于实际应用中的热通量板和土壤热特性不一致，导致热流在热通量板边缘有扭曲变形[11]，进而导致在应用式（1）～式（5）时，实际热流和该公式给出的预测值有较大的误差。1961年，Philip基于稳态热传导理论，提出了修正参数的概念：

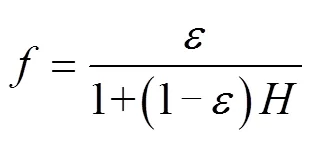
对于边长为，厚度为的方形薄板：

对于直径为、厚度为的圆形薄板：

修正后的热通量Phi为：

Philip修正公式是基于稳态热传导条件，即土壤内各点温度不随时间的变化而变化。而在实际测量当中，环境温度多为瞬态而非稳态，此时Philip修正公式是否还适用，有待验证。

1.2 计算机模拟设计

本研究应用COMSOL 版本中的传热模块进行模拟。稳态分析指在模拟所给定的条件下，达到稳定不变（温度、热量流动等状态不变）时对模型的温度分布、热流分布等的分析；瞬态分析指在模拟所给定的条件和指定时间内对温度分布、热流分布等随时间变化的分析。本文的模拟条件不考虑热对流的存在，所以采用传热模块中的传导部分，分别建立模型，进行稳态分析和瞬态分析。本文选取两种土壤分别在三种含水量下进行计算机模拟，所用参数来自参见文献[12]，具体参数值见表1。

本研究采用HFP01型热通量板为模拟对象。在土壤中测量热通量时，将周围土壤以及热通量板看成一个圆柱体集合体，从而简化为3D柱状模型。其中，土柱的直径设定为40 cm，厚度为10 cm；热通量板的直径为8 cm，厚度为0.5 cm。将热通量板水平放置，且埋藏深度分别设定为1 cm，2 cm和5 cm。由于圆柱体为中心对称图形，所以可将维度从3D简化为2D轴对称。如图1所示，由于轴对称特性只需模拟对称轴右侧区域，以便减小计算量。土柱上边界为恒定热流边界，恒定热通量设定为150 W·m–2[13]；两侧边界为绝热边界；下边界为狄式边界，恒定温度为20℃。模拟土壤的子域参数设定如表1所示；热通量板的子域参数设定依据文献[14]，热导率为0.8 W·m–1·K–1，热容为1 300 J·kg–1·K–1，密度为 1 700 kg·m–3，初始温度均为20℃。在瞬态模拟研究中，时间步长设定为0︰0.5︰1 800，即从=0 s时刻运行至=1 800 s时刻，共计30 min，以0.5 s为计算间隔。稳态模拟是模型温度及热流达到稳定时的状态，所以无需设定时间步长。

本文通过瞬态模拟，分析土壤热通量板测量误差及影响因素。土壤热通量测量值为HFP01板中直径为3 cm圆形中心区域的热通量平均值（图1中的①）；为了消除热通量板边界的热流扭曲造成的误差，本研究将土壤热通量的理论值设定为埋藏深度处接近板右侧边界的热通量平均值（图1中的②），通过比较测量值与理论值的差值，分析土壤含水量与装置埋藏深度对测量误差的影响，并且对模型的温度场与热流分布进行了稳态模拟，分析测量误差的来源。

①：模拟中的热通量测量值取值区域；②：模拟中的热通量理论值取值区域；③：对称轴；④：模拟中的恒定热流边界；⑤：实验中的加热膜位置

本文通过稳态模拟分析两种土壤在不同含水量的情况下，在三个埋藏深度处测量值、Philip修正值与理论值相对误差，比较不同条件对Philip修正效果的影响。由于目前的热通量板中央的传感器尺寸设置不同，本文还模拟了当热通量板内的传感器半径分别为1 cm、2 cm、3 cm和4 cm时对热通量测量误差的影响。

此外，本文将瞬态模拟与稳态模拟相结合，利用稳态模拟中计算出的Philip修正参数，计算出瞬态模拟的热通量的瞬态修正值，并与稳态模拟中的理论值进行对比，从而考察Philip修正公式在瞬态条件下的适用性。

1.3 室内实验设计

室内实验采用取自官厅水库的砂土，并设置3个水分梯度：0.00 g·kg–1，20.0 g·kg–1和150 g·kg–1。分别对三个含水量的容重、热导率、体积热容量等物理参数进行测量，各参数均重复6次，结果如表2所示。

表1 计算机模拟所用到的物理参数

表2 室内试验土壤样品的物理属性

实验在有机玻璃容器内进行，容器的内径为12 cm，高度为10 cm，厚度为0.5 cm，中间深度5 cm处安置加热膜，加热膜的直径为12 cm，厚度为0.27 cm，加热膜上方安置热通量板装置，热通量板水平安放在加热膜2 cm下方，如图1整体区域所示。热通量板装置与数据采集仪（型号CR1000，Campbell Scientific公司，Logan，UT）连接，采样频率设定为1Hz。对于不同的土壤含水量，均设置6次重复，取平均值作为测量值，再应用Philip（1961）修正公式进行校正得到修正值。通过满足定解的条件式（1）～式（2），应用式（1）～式（4）作为理论参考值。本文获得的相对误差均通过计算测量值与理论值的偏差得到。此外，为了表述方便，文中出现的符号如表3所示。

表3 文中出现的符号及定义

2 结果与讨论

2.1 热通量板法测量精度的主要影响因素

两种土壤在三种含水量情况下，均为埋藏深度越深测量准确度越低。如图2（a）所示，含水量为0.00 g·kg–1时，土壤的热导率小于热通量板的热导率，使得测量热通量大于土壤实际热通量，相对误差为正；含水量为200 g·kg–1和400 g·kg–1时，相对误差为负。两种情况的相对误差绝对值均随着埋藏深度的增大而增大。这是由于在计算机模拟中，表面被设定为恒定热源，埋深越深则热通量板的边界效应越明显，热流扭曲越大，从而偏离理论值越远。

图2 埋深不同（a）或土壤含水量不同（b）时热通量板测量的相对误差

两种土壤在三种埋藏深度的情况下，含水量影响大致相同，干燥土壤的测量误差较大；具有一定含水量的土壤的测量误差较小。如图2（b）所示，当热通量板埋藏深度为5 cm时，相对误差由小到大依次排列为：含水量为200 g·kg–1的黏土、含水量为400 g·kg–1的黏土、含水量为400 g·kg–1的砂土。

结果表明，土壤热通量测量的相对误差大小取决于土壤热导率与热通量板热导率的差异程度，热通量板的热导率越接近土壤的热导率，测量结果的准确度越高。

2.2 计算机模拟热通量板的误差来源

热通量板放入土壤后，在热通量板的边界会产生温度与热流的不均匀分布。当土壤热导率高于热通量板热导率时，在热通量板与土壤交界处，土壤中的温度梯度小于热通量板内温度梯度，所以热通量板的放置影响了土壤中温度的分布。其热流分布如图3（a）所示，土壤的热通量高而流经热通量板的热通量低。以热通量板的径向作为横坐标，土壤热通量为纵坐标，如图4（a）所示，在交界处，土壤热通量对应有峰值出现，而流经热通量板的热通量则出现低谷。当土壤热导率低于热通量板热导率时，以埋藏深度为1 cm的含水量为0.00 g·kg–1的砂土为例，如图3（b）和图4（b）所示，变化规律相反：在交界处，土壤热通量对应有低谷出现，而流经热通量板的热通量出现峰值。

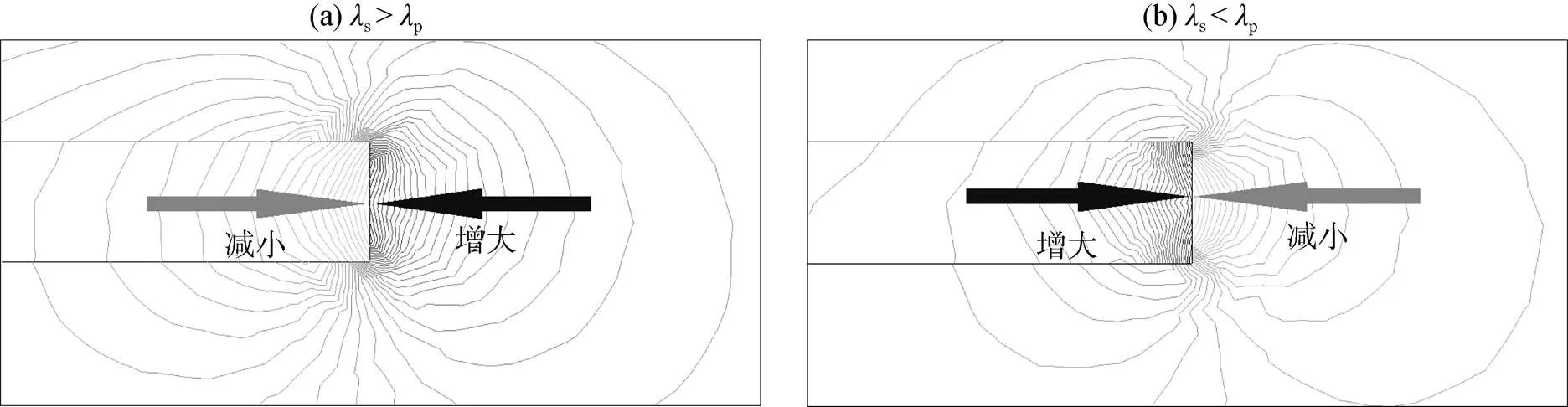
注：同一曲线上热流密度处处相等，且热流方向垂直于等温曲线Note：Heat flux density is constant on the same curve，and its direction is perpendicular to the isothermal curve

图4 热通量板与土壤热通量的水平方向分布模拟图

上述两种情况显示，由于热通量板和土壤热导率的差异，导致在热通量板边界处，土壤热通量与热通量板中热通量的不同，即在相同的埋深处，热通量板边界处产生了热通量的突变值。

2.3 Philip修正公式的效果

稳态模拟结果表明（如表4所示），传感器半径越小，Philip修正效果越好；修正前后相对误差均随深度增加而增大；Philip修正公式在具有一定含水量的土壤中应用性较好，而应用于干燥土壤时较差。瞬态模拟结果表明，Philip修正公式在干燥土壤中应用性较差，在具有一定含水量的土壤中应用性较好（如图5（a）所示）；在埋深2 cm和5 cm处的应用性好于埋深1 cm（如图5（b）所示）。

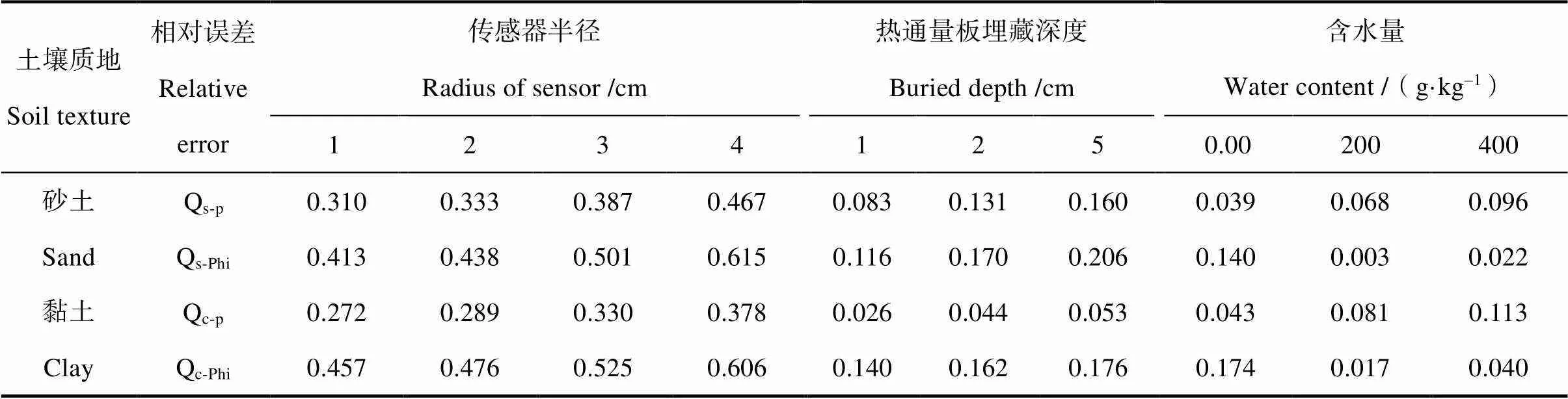
表4 稳态模拟Philip修正效果

对三种含水量的砂土进行室内实验，应用式（1）～式（9）的结果作为理论值。以Carslaw理论值GE-C作为横坐标，以测量值GE-P和GE-Phi作为纵坐标，对数据进行过原点的直线拟合分析，并以1︰1线为参考，分析Philip的修正效果，如表5所示。在土壤含水量为20.0 g·kg–1时，HFP01的测量准确度较高，所以修正公式的修正效果并不明显；在土壤含水量为0.00 g·kg–1和150 g·kg–1时，虽然修正后的拟合直线斜率均较未修正的拟合直线斜率更加接近于1，但是校正后的拟合直线斜率与1仍存在偏离，说明修正值与理论值之间仍存在偏差。

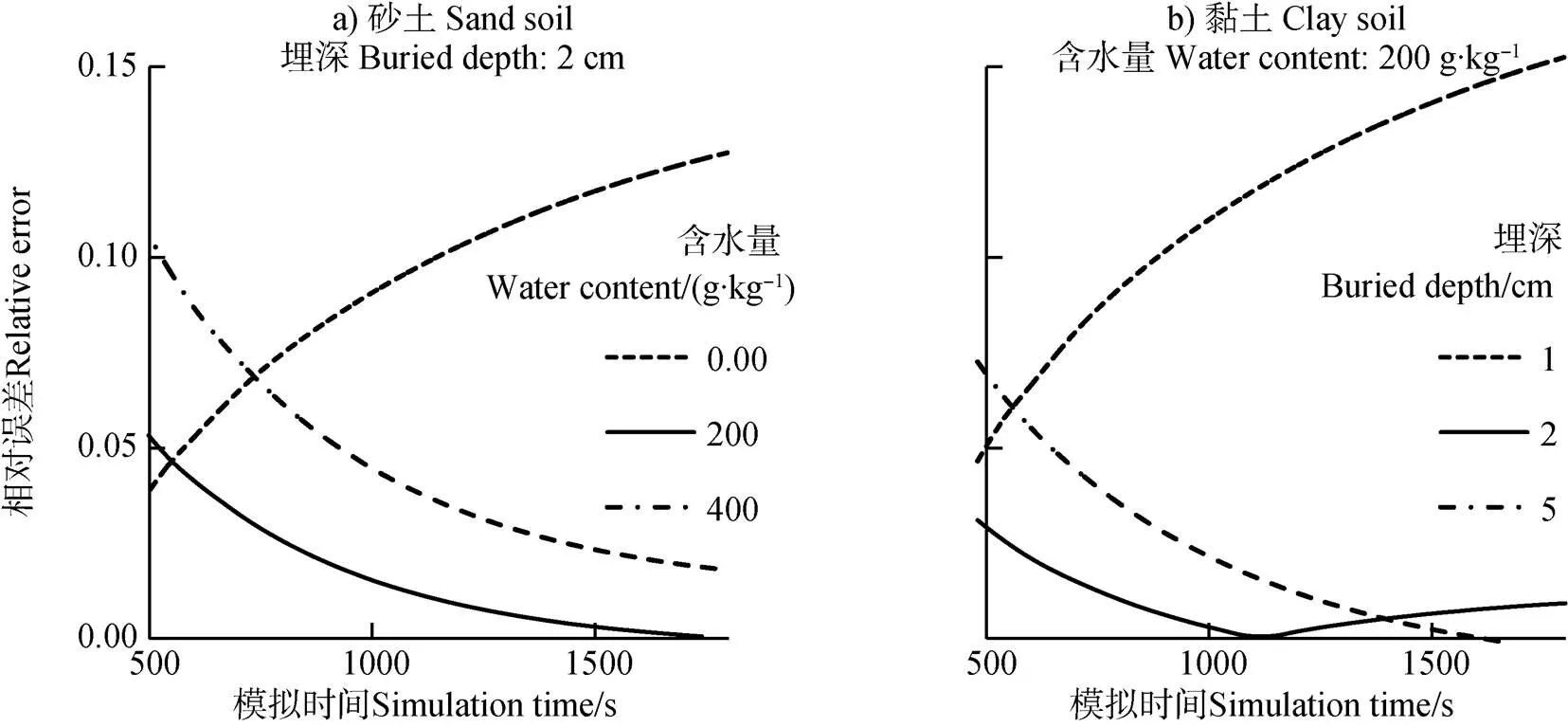
图5 埋深不同（a）或土壤含水量不同（b）时热通量板测量的相对误差

表5 室内实验检验Philip（1961）修正效果

计算机模拟与室内实验结果表明，由于Philip的稳态假设处理，修正后仍存在误差。因为Philip的解是热传导方程在稳态条件下给出的，并不能应用于瞬态问题，特别是当土壤温度未达到稳定分布时。所以，在土壤温度随时间波动的情况下，Philip的解会偏离瞬态热传导方程给出的解，并导致测量误差。

3 结 论

本文采用有限元仿真软件COMSOL进行计算机模拟，直观呈现出热通量板测量准确性的影响因素。通过计算机模拟与室内实验结合，考察了Philip修正公式在瞬态条件下的适用性。结果表明：和文献所述不同[15]，热通量板测量结果的准确度并非随着埋藏深度增加而提高；本实验结果为深度越深准确度越低；土壤热导率是热通量板测量准确度的主要影响因素，热通量板的热导率越接近土壤的热导率，测量结果的准确度越高。计算机模拟证实了前人的猜测[16-17]：由于热通量板与土壤热导率的差异，使得两种材料中温度分布不同，进而由于温度梯度的差异导致在热通量板的边界产生热流的不均匀分布。Philip修正公式在干燥的土壤情况下，修正准确性较差；在具有一定含水量的土壤情况下，修正准确性较好。Philip修正理论有局限性，是因为在修正公式推导过程中，为简化运算做了很多近似，并且在土壤温度随时间波动的情况下，Philip的解会偏离瞬态热传导方程给出的解，导致了校正值与理论值间仍存在差异的现象，表明此公式有待优化。

［1］ Zhang L，Li Y Q，Li Y. Study of calculation of the surface fluxes：Review and progress. Plateau and Mountain Meteorology Research，2010，30（1）：76—80. [张烺，李跃清，李英. 地表湍流通量计算方法的研究综述. 高原山地气象研究2010，30（1）：76—80.]

［2］ Xu Z W，Liu S M，Xu T R，et al. The observation and calculation method of soil heat flux and its impact on the energy balance closure. Advances in Earth Science，2013，28（8）：875—889. [徐自为，刘绍民，徐同仁，等.不同土壤热通量测算方法的比较及其对地表能量平衡闭合影响的研究. 地球科学进展2013，28（8）：875—889.]

［3］ van Der Tol C. Validation of remote sensing of bare soil ground heat flux. Remote Sensing of Environment，2012，121：275—286.

［4］ Evett S R，Agam N，Kustas W P，et al. Soil profile method for soil thermal diffusivity，conductivity and heat flux：Comparison to soil heat flux plates. Advances in Water Resources，2012，50：41—54.

［5］ Sun C，Jiang H，Chen J，et al. Variation of soil heat flux in subtropicalforest ecosystem in China. Acta Pedologica Sinica，2013，50（5）：966—973. [孙成，江洪，陈健，等. 亚热带毛竹林土壤热通量变异特征.土壤学报，2013，50（5）：966—973.]

［6］ Barr A G，van Der Kamp G，Black T A，et al. Energy balance closure at the BERMS flux towers in relation to the water balance of the White Gull Creek watershed 1999–2009. Agricultural and Forest Meteorology，2012，153：3—13.

［7］ Foken T，Mauder M，Liebethal C，et al. Energy balance closure for the LITFASS—2003 experiment. Theoretical and Applied Climatology，2010，101（1/2）：149—160.

［8］ Sauer T J，Horton R. Heat flux. Micrometeorology in agricultural system //Hatfield J L，Baker J M. Agron Monogr47. Madison，WI：ASA，CSSA，and SSSA，2005：131—154.

［9］ Philip J R. The theory of heat flux meters. Journal of Geophysical Research，1961，66（2）：571—579.

［10］ Sauer T J. Heat flux density //Dance H，ToppG C. Methods of soil analysis. Part 4. Madison，WI：SSSA，2002：1233—1248.

［11］ Sauer T J，Ochsner T E，Horton R，et al. Soil heat flux plates. Agronomy Journal，2007，99（1）：304—310.

［12］ van Wijk W R. Physics of plant environment. 1963.

［13］ Novak M D. Dynamics of the near-surface evaporation zone and corresponding effects on the surface energy balance of a drying bare soil. Agricultural and Forest Meteorology，2010，150（10）：1358—1365.

［14］ Hukseflux. Thermal Sensors HFP01 & HFP03 Heat Flux Plate User Manual. Version 0612.

［15］ Liebethal C，Huwe B，Foken T，et al. Sensitivity analysis for two ground heat flux calculation approaches. Agricultural and Forest Meteorology，2005，132（3/4）：253—262.

［16］ Cobos D R，Baker J M. In situ measurement of soil heat flux with the gradient method. Vadose Zone Journal，2003，2（4）：589—594.

［17］ Sauer T J，Akinyemi O D，Thery P，et al. Evaluation of a new，perforated heat flux plate design. International Communications in Heat and Mass Transfer，2008，35（7）：800—804.

Measuring Error of Soil Heat Flux Plate and Applicability of Philip’s Equation for Modification

XING Zhou, QIAO Zhaoyu, LIU Gang†

(College of Resources and Environmental Science, China Agricultural University, Beijing 100193, China)

Measurement of soil heat flux is pivotal to researches on budgeting of surface heat. To measure soil heat flux, there are several ways, one of which is the heat flux plate method, simple and easy to handle, but unpredictable in accuracy.In this study, an indoor experiment was carried out in combination with computer simulation to determine errors of the measurement with the soil heat flux plate method and explore its influencing factors. In this paper, with soil deemed as homogenous medium and the heat flux plate as composite material, influences of the composite material on temperature field of and heat flux distribution in the homogenous medium. In addition, analysis was done of applicability of the modificatiton equation Philip put forth in 1961.Results show that when the soil and the plate is quite approximate in heat conductivity measurement error of the method is low and Philip’s equation is relatively low in applicability under transient conditions.The study shows that due to difference in thermal conductivity between the heat flux plate and the soil, the heat flow will distort at the edge of the plate, thus leading to occurrence of errors in the measurement. As Philip’s equation simplifies computation in the derivation process, difference is still found between calibrated value and theoretical value when soil temperature varies with time, which indicates that its application is limited in range.

Soil heat flux; Heat flux plate; Soil heat conductivity

S152.8

A

10.11766/trxb201904090423

邢洲，乔照钰，刘刚. 土壤热通量板测量误差及Philip修正公式的适用性[J]. 土壤学报，2020，57（1）：92–99.

XING Zhou，QIAO Zhaoyu，LIU Gang. Measuring Error of Soil Heat Flux Plate and Applicability of Philip’s Equation for Modification[J]. Acta Pedologica Sinica，2020，57（1）：92–99.

* 国家自然科学基金项目（41771257）和国家重点研发计划项目（2016YFD0800102）Supported by the National Natural Science Foundation of China（No. 41771257）and the National Key R&D Plan of China（No. 2016YFD0800102）

，E-mail：liug@cau.edu.cn

邢洲（1997—），女，上海人，主要从事有限元模拟土壤水热运动的研究。E-mail：emilyxing@yeah.net

2019–04–09；

2019–07–12；

2019–09–06

（责任编辑：檀满枝）