基于Markov模型的HTTP参数排序隐蔽信道检测方法
沈国良,翟江涛,戴跃伟
(1.江苏科技大学 电子信息学院,江苏 镇江 212003; 2.南京信息工程大学 计算机与软件学院,南京 210000)
0 概述
1973年LAMPSON提出“covert channel”概念,其最初的定义是建立在多安全等级(Multi-Level Security,MLS)的自动化信息系统(Automated Information System,AIS)中,主要针对在不同主体和对象间的访问控制及安全分类。如今,其主要针对高度互联的网络,实体为网络应用程序或网络节点[1],因而隐蔽信道的另一个更广泛更具适应性的定义为“策略上被拒绝但性质上允许的通信信道”。根据该定义,隐蔽信道可以延伸到网络传输的各个协议中,尤其是占据一半流量的HTTP协议,成为隐蔽通信的良好载体。
HTTP隐蔽信道分为存储式隐蔽信道[2]、时间式隐蔽信道[3]和网络行为隐蔽信道[4]。存储式隐蔽信道主要是利用HTTP协议报文中部分不关键的字段名或值嵌入隐密消息以实现隐蔽通信,如将某些保留、可选用或未定义的字段修改为经过编码的隐蔽数据[5]。传统的HTTP存储式隐蔽信道包括对URI[6]、Cookies[7]、User-Agent[8]以及网页重定向等元素进行编码嵌入隐蔽信息实现隐蔽通信。时间式隐蔽信道主要利用网络传输HTTP数据包的时间特性来隐藏信息[9],通常使用数据包的收发时间以及包间时延等特性,例如On-off是一种典型的时间式隐蔽信道[10],它由信息发送端和接收端约定一个时间间隔,在此期间若有数据包发送代表隐秘信息“1”,无数据包发送则代表隐秘信息“0”。网络行为隐蔽信道往往是在用户访问网络的行为中编码嵌入消息并表现为用户的一系列操作[11],如LiHB[12]通过数学组合的编码方式将N个请求分配到M条流中,接收端只要解码不同流对应的请求数量就能接收到隐蔽信息。
为了对抗隐蔽通信的非法使用,实现网络安全的可管可控,研究者们也陆续研究各种检测算法。文献[13]提出网络场景检测方法为用户提供使用潜在隐蔽信道的场景,但是面对实际网络中的复杂场景,其检测性能并不理想。文献[14]通过基于直方图的算法对正常通信时间序列与隐蔽通信的时间序列分别建模,并提出一种基于Kolmogorov-Smimov(KS)统计量的检测算法。文献[15]根据时间式隐蔽信道的特点,提出检测波形形状的检测方法。上述2种方法对数据包的包间间隔等时间特性进行统计分析,取得了较好的检测效果,但不适用于检测网络行为信道。文献[16]提出基于校正熵的统计检测方法,并取得良好的检测率,但该方法并不能实现对存储式信道的检测。针对存储式信道的检测,文献[17-18]采用基于SVM的机器学习检测算法,利用正常数据和含密数据的差异进行检测;文献[19]提出基于K-means聚类的检测方法,对HTTP协议GET消息编码的隐蔽信道进行检测。
HTTP协议中的参数排序隐蔽信道利用请求报文自身排序编码隐蔽信息,而上述检测方法主要通过包间间隔提取特定属性,无法对该信道进行检测。因此,根据信道需要频繁改变其报文的特性,本文提出一种基于Markov模型的HTTP参数排序隐蔽信道检测方法。
1 HTTP协议中的隐蔽信道
HTTP是万维网能够可靠交换文件(包括文本、声音、图像等各种多媒体文件)的重要基础。HTTP的报文分为请求报文和响应报文。HTTP请求报文由请求行、请求头部和请求正文组成,如图1所示。其中,请求头部包含有关客户端环境以及请求正文的有用信息。请求头部由“关键字∶值”对组成,每行一对,关键字和值之间使用英文符号“∶”分隔。采用Wireshark捕获到的HTTP请求报文如图2所示,其中Host、Connection、User-Agent及Accept等都是比较常见的报文信息,提供了使用浏览器类型、接收对象类型等信息。

图1 HTTP请求报文的一般格式

图2 Wireshark捕获的HTTP请求包
HTTP协议的参数排序通信隐藏算法[20]对序列{Ai|0≤i 图3 参数排序隐蔽通信的原理 该方法不会在HTTP报文中插入额外的字符,只是通过改变其原有的排序达到隐藏消息的目的。因为在不同操作系统、浏览器下对于同一功能产生的HTTP报文表述形式差别很大,所以在HTTP报文中这些关键字经常被忽略。因此,利用上述特性构建的HTTP参数排序隐蔽信道,不会引起正常通信的异常,并且在少量样本下,人们无法判断该数据包是正常通信或者隐蔽通信引起的关键字缺失。但是该隐蔽信道的通信与正常通信的区别在于,隐蔽通信为了传输信息需要频繁改变报文,而正常通信的报文通常变化不会很大,且变化频率较低。假设HTTP数据包的报文对应一种状态,那么隐蔽通信的状态转换将比正常通信更为频繁。因此,可以通过大量数据建立正常通信和隐蔽通信的模型来衡量两者的差异性。Markov模型是一种成熟的统计模型,其核心思想是每个状态值只取决于前面一个状态而与其他状态无关[21]。本文将数据包报文转化为对应的状态,通过建立正常通信和隐蔽通信的Markov模型状态转移概率矩阵,用相对熵来衡量两者之间的差异。 Markov链是一个时间和状态都是离散的马尔可夫过程。假设数据链X={x1,x2,…,xn}中任意一个变量xt的值都在有限集E={0,1,…,n}中,即当n≥1时,i1,i2,…,in∈E,则式(1)成立。 p{xn=in|xn-1=in-1,xn-2=in-2,…,x1=i1}= p{xn=in|xn-1=in-1} (1) 数据链X={x1,x2,…,xn}即为一个具有可数状态的Markov链,其每个状态值只取决于前面一个状态而与其他状态无关。对于任意i,j∈E,从时刻n-1到时刻n的转移概率由式(2)给出。 p(xn=in|xn-1=in-1)={xn=j|xn-1=i}=pij (2) (3) 序列X={x1,x2,…,xn}的状态转移概率矩阵可由下式给出: (4) Markov链的初始状态为: Q={q1,q2,…,qδ} (5) 其中,qi表示状态值为i(i=1,2,…,δ)的概率,qi满足式(6)。 (6) 其中,N表示序列的总长度,Ni表示序列中状态值为i的总个数。 在HTTP协议中,客户端发送的请求报文中的关键字可能出现或者不出现,将所有可能排列情况视为独立状态,一个HTTP数据包的报文状态就是一个随机且有限的状态集,其当前状态只与上一个状态有关,因此,可以使用Markov链构建HTTP数据包的状态模型。 在HTTP参数排序隐蔽信道中,每一个关键字的出现与否都是组成某一时刻状态的因素,由于关键字种类繁多且正常通信中使用极少数,为了便于呈现,本文选取其中4个最为常见的关键字构建隐蔽信道,分别为Host、Connection、Accept和User-Agent。通过HTTP数据包关键字的状态对应的二进制序列,计算得到HTTP数据包的状态位。 Ek=8×EHost+4×EConnection+2×EAccept+1× EUser-Agent (7) 由于每一个关键字都有2种取值,因此可计算得到HTTP数据包共有16种状态位,即E={0,1,…,15}。 对一个HTTP包数据集Tn={t1,t2,…,tn},根据式(3)和式(4)求得其Markov链状态转移概率矩阵,建模过程为:提取数据包中的关键字,转化为二进制序列,利用式(7)计算得到HTTP包的状态,训练并得到Markov模型转移概率矩阵。因为要检测信道是否为隐蔽信道,所以除了要建立用于比较的实际HTTP包Markov模型转移概率矩阵,还要建立每一个待测数据集的Markov模型转移概率矩阵。 本文采用相对熵对建立的模型进行比较,相对熵可以用来衡量2个概率分布之间的差异。假设p(x)和q(x)是离散随机变量X中的2个概率分布,则p和q的相对熵为: (8) p(x)和q(x)分布相同,则相对熵等于0;两者之间差异越大,则相对熵越大。本文利用相对熵的定义来计算正常数据流和待测数据流的Markov模型的状态转移概率矩阵的差异,计算公式为: (9) 2个矩阵的差异越大,则其相对熵越大。因此,可以通过设定阈值来判断数据流是否异常,大于阈值则为隐蔽通信数据流,小于阈值则为正常通信数据流。正常通信数据流由于HTTP包的报文信息比较稳定,没有出现4个关键字均不出现的情况,所以部分状态值的数量为0,导致当利用式(3)和式(4)计算数据流转移概率矩阵时,出现0元素及部分元素无意义,从而无法用式(9)计算2个模型之间的相对熵。因此,设定这些元素为一个很小的概率pij=1.0×10-6。同样,将这种方法应用到待测数据流的转移概率矩阵建立中。基于Markov模型的检测算法总体流程如图4所示。 图4 本文算法检测流程 本文实验收集40 000个正常HTTP数据包和20 000个异常数据包。正常数据包通过Fiddler捕捉用户电脑与互联网之间的HTTP通信得到。将待发送消息编码成二进制信息,并以每4位嵌入一个HTTP包,根据第1节介绍的隐蔽信道构建方式,结合发送的二进制信息利用Fiddler篡改正常数据包报文中的4个关键字,获取异常数据包。实验首先通过模型训练设置合适的相对熵阈值,这是判断数据流是否异常的关键;其次设定一个合适的窗口大小,因为窗口过小容易减小待测模型与正常模型之间的差异,从而降低检测效果,窗口过大会影响检测速度;最后计算在正常数据流中嵌入50%~100%的异常数据包时的检测率。 本文实验分别取10 000个正常和含密的HTTP数据包作为训练集,其余用作测试集。以1 000窗口大小分割测试集为20组,含密数据和正常数据各10组。计算每一组中各个状态值的数量,并求出10组数据的均值,结果如图5所示。可以看出,异常数据包状态值从0到9数量较为均匀,在100上下浮动,状态值大于8的数据包数量均在50左右;正常数据包状态值低于8的数量为0,这是因为正常数据包中都包含Host关键字,并且大部分状态值都是15。根据建立训练集的Markov转移概率矩阵与实际模型求相对熵,结果如图6所示。 图5 每组中的状态值数量均值 图6 训练集与正常模型相对熵的值 从图6可知,异常数据流与选定的实际模型之间相对熵较大,正常数据流则偏小,结合图5中的结果,这是因为正常数据流中状态值为12、14和15的数据包占多数,与实际模型差异较小,而异常数据流中各个状态位的数据包较为均匀,与实际模型差异较大。其中,与异常数据流的最小相对熵值接近2.5,与正常数据流的最大相对熵值接近1.5,因此,设定阈值为2,即当测试集与实际模型的相对熵值超过2时,判定为异常数据流,否则为正常数据流。 为了分析窗口大小对检测率的影响,在设定相对熵阈值为2,按不同窗口对测试集切割分为若干组,计算其检测率,结果如图7所示。 图7 不同窗口下的检测率 从图7可以看出,窗口较小对实验的检测率影响较大。这是因为较小数据包构建的异常数据流模型容易在局部与实际模型相似,大幅减小了相对熵的值。而当窗口大于等于1 000时,该方法均可取得较好的检测效果,因此,可将窗口设置为1 000。 嵌入率是指在一个数据流中包含的异常数据包占总数据包的比例。在相对熵阈值为2,窗口大小为1 000情况下,计算不同嵌入率下的检测率和误报率,结果如图8所示。由于嵌入率较低时,检测率偏低,因此在图8中只显示嵌入率大于50%的数据。 图8 不同嵌入率下的检测率和误报率 Fig.8 Detection rate and false alarm rate at different embedding rates 从图8可以看出,嵌入率在50%至60%的区间内,检测率较低。这是因为数据包中大量正常数据包的存在,使得由状态15向状态15的转移依旧占据主导地位,导致与实际模型计算相对熵时偏小,最终影响检测率。在嵌入率不小于70%时,所有状态值的数量趋于平均,加大了与实际模型的差异,检测率可以保持在97%以上。当嵌入率为100%时,检测率高达99%,并且保持极低的误报率。 本文分析基于HTTP的二进制排序隐蔽信道特征,利用隐蔽通信的状态转换比正常通信更频繁的特点,将基于Markov模型的检测方法用于隐蔽信道的检测,并以待测数据包和正常数据包的转移概率矩阵之间的相对熵作为判别标准。实验结果表明,该方法在窗口大小为1 000时,能够对嵌入率超过70%的异常数据流保持较高的检测率。但是本文没有考虑到该方法对于其他隐蔽通信方式的适用性,下一步将对其通用性进行研究。
2 基于Markov模型的检测算法
2.1 Markov链
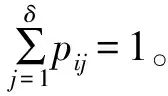
2.2 Markov转移概率矩阵
2.3 本文检测算法

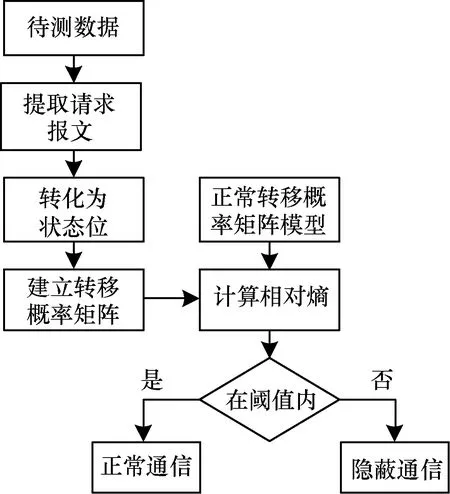
3 实验与结果分析
3.1 相对熵阈值的选定


3.2 窗口大小的选定

3.3 嵌入率对检测结果的影响

4 结束语

