反演法求小麦面团在冻结温度范围内的热导率

,2,3,2,3,2,3,*

(1.郑州轻工业大学食品与生物工程学院,河南郑州 450002;2.河南省食品生产与安全协同创新中心,河南郑州 450002;3.河南省冷链食品质量安全控制重点实验室,河南郑州 450002, 4.郑州思念食品有限公司,河南郑州 450011)

面团制品(包括面包、馒头、包子、水饺等)的多个加工都涉及到传热,热物性数据在面制品食品速冻加工中尤为重要[1-2]。食品加工操作的建模和设计都以其热物性数据为基础[3],热导率是其中重要的物理量。了解食品的热导率可以用来确定食品内部的温度分布,预测食品热加工所用时间[4],并筛选出合适的加工工艺。热物性数据的精准度会直接影响到所建数学模型的精确度[5]。

热导率的测定方法主要分为两种:稳态法和瞬态法。稳态法处理简单、试验条件容易控制,但是需要较长时间,易引起误差,从而影响实验结果[6]。Kulacki等使用单板导热仪直接测量稳态热流面包屑和面包皮之间的温差,并采用傅里叶导热定律计算导热系数[7]。瞬态法实验时间短、测量结果比较准确,是较为常用的测定方法[8],但是该方法实际测量的是一定温度范围内的热导率平均值。Komastu等采用瞬态法中的热线法测量了发酵面团在0～100 ℃的热导率[9]。稳态法及瞬态法在面团及其制品热导率测定中皆有应用,但都各有缺点。反演法是确定热导率的另一种方法,在一个传热过程中,根据食品的初始温度、边界条件,确定一个或几个未知参数的方法,称为反演导热问题[10]。解决反演问题的基本原则是使温度测定值与模型预测值之间的差异达到最小,通常采用非线性最小二乘法表示两者之间的差异[11]。反演法可以避免上述稳态法和瞬态法的缺点,同时由于所得参数是根据温度测定结果进行反演的结果,这将有利于在进行正向的模拟计算时给出更接近实测温度的预测温度值。反演法在食品加工过程中应用较少。Silva等采用反演法推算蘑菇切片干燥的过程中的热导率[12]。Martins等通过反演法确定冰冻青豆在解冻过程中的热导率[13]。

前人大多对面团高温下的热导率进行了测定[14-17],但对冷冻温度范围内的热导率研究较少[18-19]。本文首先测定小麦面团的比热,然后根据面团特定位点的温度,通过反演计算其热导率,并进一步建立面团的热导率与温度和水分之间的定量关系,为以后实现面团制品冷冻过程的计算机模拟奠定基础。

1 材料与方法

1.1 材料与设备

河南金苑饺子粉(含水量11.62%、蛋白质11.8%、脂肪1.1%)、食盐 均购于郑州市高新区丹尼斯超市。

BN-100L浸渍式速冻机 广州市宝能机电设备有限公司;Q20差式量热扫描仪 美国TA公司;AT4508多路温度测试仪 常州安柏精密仪器有限公司;JA1203电子天平 上海越平科学仪器有限公司。

1.2 面团制备

100 g饺子粉中加入1 g盐,再分别加入42.55、49.80、57.82 mL水混合制成水分含量(moisture content,即MC)分别为38%、41%、44%的面团,在室温下静置1 h,备用。

1.3 面团比热的测定

使用差式量热扫描仪采用三步法测定面团的比热[20]。将称重后的两个空坩埚放入差式量热扫描仪中,首先在40 ℃平衡5 min,然后以10 ℃/min的速率冷却到-35 ℃;在-35 ℃平衡10 min后,以同样的速率加热到40 ℃,由此可以得到基线。再将标准物(铝)、空盘以同样的程序运行[21]。最后称重(10±1) mg的面团放入铝坩埚中,并用铝盖覆盖密封防止水分散失,以相同程序扫描。由式(1)计算得此面团的比热[22]。

式(1)

式中,m为示样品质量(mg),cp为比热(J/kg· ℃),P为热流率(J/s),sp为样品,cal为标样,bla为空盘。

1.4 面团冷冻过程中的温度测定

将制备好的面团从圆形铝筒一端小心塞入,要保证面团内及面团与圆筒壁无空气,再用插有热电偶的橡胶塞封紧圆筒两端,另取一根热电偶贴在圆筒表面记录其表面温度,见图1。图1中a、b是测量面团内部中心对称点左右各1 cm处温度的热电偶,此温度定义为测点温度;c是测量圆筒表面温度的热电偶;d是测量乙醇温度的热电偶。

图1 圆筒热电偶分布Fig.1 Thermocouple distribution of cylinder

将圆筒及热电偶组装完成后放在室温下平衡,待热电偶温度与室内温度基本平衡后,放进浸渍式速冻机的乙醇池内,并采用多路温度测试仪立即记录温度随时间的变化。当测点温度达到-30 ℃时停止记录。由于铝的热导率比面团的高很多,且筒壁很薄,将测得的铝铜表面温度近似地认为等于面团圆柱表面温度。

1.5 面团密度及橡胶塞参数的确定

面团密度的测量：首先向量筒中放入20 mL的水,取适量面团称量后,放入量筒,使其完全浸入水中,记录体积,最后计算出面团密度。采用相同方法测定橡胶塞密度。

胡少枝等通过热线法对几种橡胶制品的热导率进行测定,发现多种橡胶制品的热导率在(0.191±0.1) W/m·k之间[23]。周贵斌等通过DSC法对各种混炼胶比热进行了测量,发现在50～120 ℃温度范围,混炼胶的比热为1300～2100 J/kg· ℃[24]。本研究中选定橡胶塞热导率为0.1 W/m·k、比热为1700 J/kg· ℃。

1.6 模型建立

假设圆筒中塞满面团,橡胶塞与面团间无缝隙。将试验所用圆筒看作质地均匀的圆柱体,取1/4建立几何模型作为研究对象。认为降温时面团及橡胶中的热量传递遵循傅里叶第二导热定律[25]:

式(2)

式中,T为温度(K),r为圆筒半径(m),ρ为密度(kg/m3),λ为导热系数(W/m·k),Cp为比热(J/kg· ℃);t为时间(min)。

1.7 反演计算

采用COMSOL软件进行反演计算。先建立圆筒中心对称二维几何模型,然后利用其固体传热模块对传热过程进行分析计算。将橡胶塞各参数输入,并通过内插函数将面团比热、测点温度、表面温度数据导入,用分段函数式(3)表示面团的热导率随温度的变化[26]。

式(3)

式中,k为热导率(W/m·k),Tsf为初始冻结点温度(K),T为面团测点温度(K);kf、b、c、d为待定模型参数。

采用优化求解器,在表面温度、面团测点温度、面团比热C输入的情况下,将kf、b、c、d四个参数确定一个大概的值并设定初始值上下限,通过式(4)求出偏差平方和(SS),SS最小时计算出的参数即为各参数最佳值[27]。

式(4)

式中,Tobs为测量的面团测点温度,Tpred为预测的面团测点温度。

2 结果与讨论

2.1 不同水分含量面团的比热及校正

不同水分面团的比热随温度的变化见图2。水分结冰前,比热随温度的变化很小,相变发生时比热随温度变化幅度较大。在冻结温度范围内,由于面团中水分结冰释放出潜热,使得表观比热大幅度上升;随水分冻结的完成,表观比热在达到最大值后骤降。面团的比热随着其含水量的增加而增加,这是因为水的比热大于干物质的比热,面团中的水分越多,单位时间内放出的热量也就越多。Xu等通过差式量热扫描法测定了面团在冷冻温度范围的表观比热,其结果与本文的大致相同[19]。图2中,MC38%面团比热、MC41%面团比热、M44%面团比热分别表示小麦面团水分含量为38%、41%、44%时面团比热随温度变化的曲线;MC44%面团比热峰形校正表示水分含量为44%面团峰形校正后比热随温度变化的曲线;MC44%面团比热冰点校正表示水分含量为44%面团峰形校正后比热随温度变化的曲线。

图2 温度对含水量38%、41%、44% 面团比热的影响及44%面团比热校正Fig.2 Effect of temperature on specific heat of dough with water content of 38%,41%,44% and correction of specific heat of dough with moisture content of 44%

对于比热曲线的校正分为两步,第一步为峰形校正,第二步为冰点校正。因为DSC测定过程中面团内部传热时间长,造成面团内外温差较大,导致比热曲线峰形向右变形(见图2),此时需要对比热曲线进行校正[28]。校正公式见式(5)。

式(5)

式中,C′p(T)为DSC测定的比热(J·kg-1· ℃-1),Cp(T)为校正之后的比热(J·kg-1· ℃-1),τ为时间常数。τ确定的依据是要确保原比热曲线下面积与校正后比热曲线下面积相等。

为便于观察,图2仅给出了对含水量44%面团比热的峰形校正结果,其时间常数τ=7.1。校正之后的比热曲线峰值更高,且在达到初始冻结点后比热下降趋势更陡,这与Wang等的结果相一致[29]。

冰点校正:由于初始冻结点发生偏移,根据浸渍冻结过程中测得的面团冷冻曲线确定初始冻结点,对达到冰点后比热骤降段和比热大致平衡段做切线,切线的焦点即为初始冻结点[30],将DSC曲线向左平移使曲线初始冻结点与根据冷冻曲线的确定的初始冻结点重合。图2中含水量44%面团比热冰点校正是对峰形校正进行冰点校正的结果,将曲线整体向左平移了3.5 ℃。含水量38%面团曲线需向左平移5.6 ℃;含水量41%面团曲线需向左平移4.4 ℃。经过两次校正后的比热用于后续的热导率反演计算。

2.2 不同含水量面团浸渍冻结过程中的温度变化

对于不同水分含量的面团进行浸渍冻结,冷冻曲线见图3。由图3可以看出,面团的测点温度先缓慢下降,通过滞后期后温度下降速度加快;在达到冰点时,温度下降速度大幅度降低,穿过最大冰晶生成带后,温度下降速度剧增。

由图3可看出,随面团水分的增加,面团的测点温度降温速率反而变慢,同时冰点升高。38%含水量面团的温度下降最快,穿越最大冰晶生成带及达到-30 ℃所用时间最少。其主要原因是,水的比热比面团干物质的大,高水分面团的比热较大,冷冻过程中需要释放出的热量变较多,也就需要更长的冷冻时间。

采用反演法计算热导率时需要样品的表面温度作为输入参数。在圆筒刚被放入浸渍冷冻机内时,表面温度陡然下降,到达-5 ℃时开始缓慢下降,同时观察到表面温度随着圆筒内面团水分的增加而略有上升。

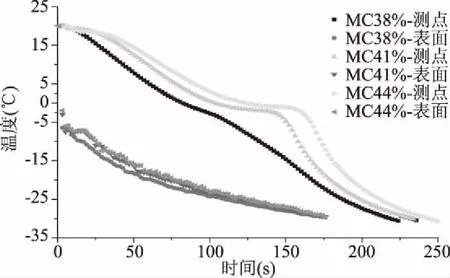
图3 面团浸渍冻结时测点温度 及圆筒表面温度随时间的变化Fig.3 Change of specified-point and cylinder surface temperature with time at dough immersing and freezing注：MC38%-测点、MC41%-测点、M44%-测点分别表示小麦面团水分含量为38%、41%、44%时的测点温度曲线;MC38%-表面、MC41%表面、MC 44%表面分别表示小麦面团水分含量为38%、41%、44%时的表面温度。

2.3 反演法求不同含水量面团的热导率

通过COMSOL软件模拟计算不同时间面团的测点温度,以SS最小为优化目标,可以得到式(3)中四个参数kf、b、c、d的值,见表1。由式(3)计算出不同含水量面团在-30～30 ℃的热导率,见图4。在温度到达初始冻结点前,面团的热导率随温度的降低而缓慢下降;到达初始冻结点后,面团的热导率随温度的降低而升高。在冷冻范围内,由于冰的质量分数增加,热导率随着温度的降低而增加。热导率也取决于含水量,随着面团含水量的增加而升高。

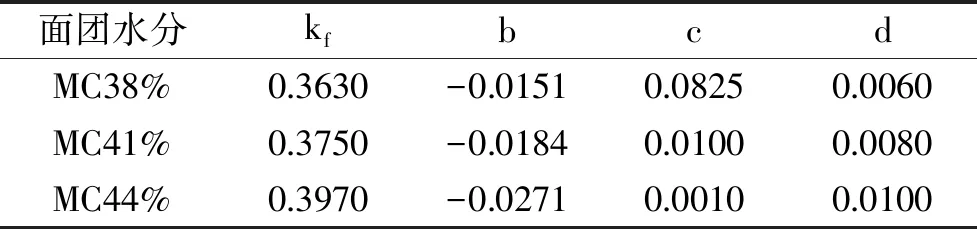
表1 式(3)中的参数值Table 1 Values of some parameters in Eq.(3)

由表1可以看出,随着面团水分的增加,kf、d的值随之增加,参数b、c的值反而减小,虽然c值随水分增加变化较大,但对反演计算结果影响不大,所以c值采用平均值,同时分别就kf、b、d与水分间关系做线性回归,所得方程分别为:

kf=0.5667x+0.146

式(6)

b=-0.1x+0.0228

式(7)

d=0.5667x+0.146

式(8)

将所得到的线性方程代入式(3),可以计算不同水分面团的热导率随温度的变化,见图4中曲线a、b、c。图4可以看出,如此计算出的热导率与采用原参数计算出的热导率相比,只有在冷冻范围内初始冻结点处略有不同。为此,可以采用式(3)结合式(6)～式(8)综合表示水分含量和温度对面团冷冻过程中热导率的影响。

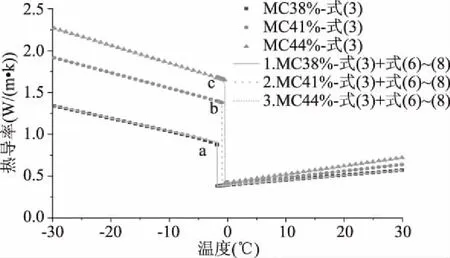
图4 面团不同水分及参数的热导率变化Fig.4 The change in thermal conductivity of dough at different moisture and parameters

Rask等测定了不同含水量面团在不同温度下的热导率,其中含水量43.5%面团在-43.5、-22、23 ℃时的热导率分别为0.92、0.88、0.46 W/m·k;含水量46.1%的面团在-38、19 ℃的热导率分别为1.03、0.5 W/m·k[31]。Kumcuoglu等采用针状探针法测定了土耳其传统发酵面团在25～50 ℃温度范围内的热导率,将冷冻范围内面团热导率确定在0.4～2.0 W/m·k,0～50 ℃的热导率确定在0.4～0.8 W/m·k之间,这些结果与本实验测得的结果大致相同[18]。

图5依次是含水量38%、41%、44%面团浸渍冻结时的测点温度实测值及用COMSOL软件模拟计算的温度值。可以看出实验结果与模拟的温度变化趋势基本一致,这说明建立的模型是可靠的,反演计算出的热导率是可信的。在冰点上,温度模拟结果与实验结果相差很小,冰点下的曲线略有差异,其中含水量38%面团较为明显。模拟结果误差可能是由于速冻机乙醇池内温度不均匀导致的。

图5 含水量38%、41%、44%面团的测点温度及模拟温度Fig.5 The specified-point and simulated temperature of dough with the water content of 38%,41% and 44%

2.4 模型对橡皮塞参数的敏感性分析

由于本模型中所采用的橡胶塞比热及热导率均为前人的测定值。为此,实验就模型对橡皮塞参数的敏感性进行了分析。图6是橡皮塞热导率、比热分别变化±10%后模拟计算出的面团温度。由图6可以看出,热导率、比热上下波动10%对冻结曲线几乎无影响。由此可以推断出,橡胶塞比热及热导率的选定对面团测点温度的影响较小。

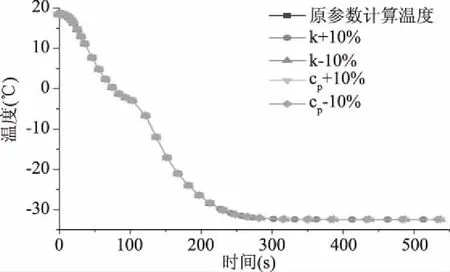
图6 橡皮塞比热及热导率上下波动10% 对38%水分面团测点温度曲线的影响Fig.6 The influence of 10% up and down fluctuation of rubber stopper specific heat and thermal conductivity on specified-point temperature curve of dough with the water content of 38%

3 结论

随面团含水量的增高,面团测点温度曲线下降趋势变缓;同时冰点升高,冻结时间变长。在冷冻范围内,三种含水量面团的比热随其含水量的增加而增加,随着温度的降低,面团的热导率逐渐降低,但是当面团的温度刚降至冰点后,面团的热导率急剧上升,然后又呈缓慢上升趋势;相同温度下,面团水分越高热导率越大。建立的面团模型可以同时预测水分和温度对热导率的影响,这可为速冻面制品在冷冻范围内的加工提供基础数据。