动态需求低碳开放式选址—路径问题
蒋海青,赵燕伟,徐兆军,柳 青,张景玲
(1.中国计量大学 现代科技学院,浙江 杭州 310004; 2.浙江工业大学 特种装备制造与先进加工技术教育部重点实验室,浙江 杭州 310014; 3.浙江西子重工机械有限公司,浙江 海宁 310021)
0 引言
目前,实现“低能耗、低排放”的绿色物流正成为物流业的发展方向,作为物流的重要组成部分,低碳选址及路径优化问题研究受到广泛关注。Dukkanci等[1]于2015年首次将低碳路径与低碳选址相结合,提出了最小化碳排放目标的选址—路径模型;Koç[2]将时间窗引入绿色选址—路径问题,分析了速度对选址、路径燃油消耗及碳排放量的影响;Eliana等[3]研究了多目标绿色选址—路径问题(Location-Routing Problem, LRP),建立了最小化燃油消耗及总成本的多目标混合整数线性规划;Eliana等[4]进一步对绿色开放选址—路径进行研究,构建了最小化运作成本及环境影响的模型,并应用epsilon约束技术求解模型;Chen等[5]研究了供应链网络的低碳LRP,建立了最小化成本及环境影响的双目标LRP模型,并设计了带精英策略的非支配排序的遗传算法(fast elitist Non-dominated Sorting Genetic Algorithm, NSGA-Ⅱ)与禁忌搜索算法(Tabu Search, TS)相结合的多目标混合算法NSGA-Ⅱ-TS进行求解;冷龙龙等[6]设计了量子超启发算法求解低碳LRP。
上述关于低碳LRP的研究主要针对静态问题,动态需求LRP的顾客需求实时改变,这种问题广泛存在于应急物流、急救服务等场景下。对动态需求LRP的研究由Laporte等[7]首次提出将动态问题分解为多个计划期,针对每个计划期内顾客的不同需求,建立了相应的模型并进行求解;Yannis[8]提出将粒子群优化算法(Particle Swarm Optimization, PSO)与3种不同的拓扑结构相结合求解动态随机需求的LRP;Yannis等[9]建立了最小化成本目标的随机需求LRP模型,并设计了克隆选择算法克隆选择算法(Clonal Selection Algorithm, CSA)与可变邻域搜索(Variable Neighborhood Search, VNS)算法,及内部局部搜索(Interated Local Search, ILS)相结合的混合算法进行求解;Zhang等[10]针对航空紧急救援任务动态需求,建立了考虑配送优先权的LRP模型,并设计了相应算法,以求解获得配送方案;Zhang等[11]解决了动态信息的多目标应急物流LRP;林殿盛等[12]研究了需求不确定的配送中心选址问题;Vincent等[13]首次建立了最小化总成本目标的开放式选址—路径问题(Open LRP, OLRP)模型,并设计了改进的模拟退火(Simulated Annealing, SA)算法进行求解。
上述关于动态LRP的研究主要关注成本目标,较少考虑选址及配送过程中的碳排放因素,本文研究考虑碳排放的动态需求LRP,针对由动态需求引起的车辆载重实时变化,借鉴文献[14]关于动态车辆路径问题(Vehicle Routing Problem,VRP)的求解思路,提出将动态需求分解为预优化及实时优化两个阶段,在实时优化阶段建立虚拟配送中心,构建了考虑碳排放变化的动态需求LRP模型,并设计包含动态量子旋转门的四阶段混合量子差分进化算法进行求解,最后通过仿真实验验证了算法及模型的有效性。
1 低碳动态需求开放式选址—路径优化模型
将问题分解为预优化和实时动态优化两个阶段进行描述,并进行如下假设:
(1)车辆匀速行驶,路上无拥堵现象,路况平稳。
(2)配送车辆类型只有1种数量不限。
(3)客户需求已知并确定,每个客户必须且只能被服务1次。
(4)不考虑配送中心选址过程中的碳排放,即只考虑建设配送中心产生的碳排放和运输过程中产生的碳排放。
(5)车辆容量有限。
(6)配送中心容量有限。
(7)任何需求点的需求量不能超过车辆的容量限额,不能分割配送。
1.1 预优化阶段选址—路径数学模型
(1)参数说明
Nm=(1,2,…,m)为配送中心集合,m为候选配送中心个数;
Nc=(1,2,…,c)为初始顾客点集合,c为初始顾客个数;
N为配送中心及顾客点集,N=Nm∪Nc,N={1,2,…,m,m+1,…,m+c};
A={(i,j):i,j∈N,i≠j}为点i,j弧集合;
K=(1,2,…,k)为车辆集合,k为车辆的个数;
QC为车辆的载重限制;
QPm=(1,2,…,m)为配送中心m的容量限制;
Fk为车辆k的固定费用;
Om为m配送中心的固定开放费用;
dij为i,j的欧氏距离,dij=dji;
CER为碳排放率,其取值与车辆所使用的燃油有关,确定的燃油值一般为固定值,本文取2.61 kg/L;
C0为车辆空载时的燃油排放率;
C*为车辆满载时的燃油排放率;
uijk为车辆k由i点到j点的实时载重;
qi为i点的需求量;
CF为碳排放费用。
(2)数学模型
1)定义决策变量:
2)目标函数:
(1)
s.t.
(2)
(3)
(4)
qjxijk≤Uijk≤QCxijk,∀i,j∈N,k∈K,i≠j;
(5)
(6)
(7)
(8)
(9)
(10)
(11)
ym≥zim,∀i∈Nc,∀m∈Nm;
(12)
xijk∈{0,1},∀i,j∈N,k∈K;
(13)
zim∈{0,1},∀i∈Nc,m∈Nm;
(14)
ym∈{0,1},∀m∈Nm。
(15)
其中:式(1)为目标函数,第1项为配送中心建设费用,第2项为碳排放费用(主要考虑了车辆类型、车辆载重变化、运输距离、燃油情况),第3项为车辆使用费用;式(2)表示每个顾客只能被服务一次;式(3)表示网络图中间节点进入弧与出去弧相同;式(4)为顾客需求限制;式(5)限制剩余需求量的取值;式(6)表示由特定配送中心服务的顾客需求量总和与该配送中心发出的货物量相同;式(7)保证车辆服务完最后一个顾客后剩下的需求量为0;式(8)保证需求量不超过配送中心容量;式(9)保证配送完后不回配送中心;式(10)保证每个顾客由一个配送中心服务;式(11)限制配送中心服务的顾客数;式(12)防止配送中心选择不可行解;式(13)~式(15)表示变量的取值。
1.2 实时优化阶段选址—路径数学模型
(1)问题描述
在实时优化阶段,由于车辆已驶离配送中心,车辆所处的位置可看作虚拟配送中心,所有前阶段未服务的顾客和新进入的顾客为待服务顾客。因为配送中心的选址属于战略层面,随顾客动态需求实时变更配送中心地址不符合实际情况,所以假设该阶段配送中心的建设成本为0,车辆固定成本只考虑新派出车辆的成本,下面对实时优化阶段进行建模。
(2)参数说明
L为第1阶段未服务顾客与第2阶段新顾客集,总数量为l;
Hk为第1阶段剩余的车辆集,其数量为hk;
NEk为第2阶段新配出的车辆集,其数量为Ne;
SYqk为第1阶段车辆k剩余的车载量;
Ng=(1,2,…,g)为第一阶段确定的配送中心集合,g为配送中心个数(g≤m);
Nh=(1,2,…,hk)为虚拟配送中心的集合,其个数与上阶段剩余的车辆数相同,为hk,虚拟配送中心的编号为g+1,g+1,…,g+hk。
(3)数学模型
1)定义决策变量:
2)目标函数:
(16)
s.t.
(17)
∀i∈L,i≠j;
(18)
∀i∈L;
(19)
qjxijk≤Uijk≤QCxijk,∀i,j∈L,
k∈(HK∪NEk),i≠j;
(20)
(21)
(22)
(23)
(24)
(25)
∀m∈Ng&∀h∈Nh;
(26)
ym+yh≥zim+zih,∀i∈L,
∀m∈Ng&∀h∈Nh;
(27)
xijk∈{0,1},∀i,j∈L,k∈(HK∪NEk);
(28)
zim∈{0,1},∀i∈L,∀m∈Ng;
(29)
ym∈{0,1},∀m∈Ng;
(30)
(31)
zih∈{0,1},∀i∈L,∀h∈Nh;
(32)
yh∈{0,1},∀h∈Nh。
(33)
其中:式(16)为目标函数,第1项为配送过程的碳排放费用,第2项为车辆费用;式(17)表示每个顾客只能被服务一次;式(18)表示网络图中间节点进入弧与出去弧相同;式(19)表示顾客需求限制;式(20)限制剩余需求量的取值;式(21)表示由特定配送中心服务的顾客需求量总和与该配送中心发出的货物量相同;式(22)保证车辆服务完最后一个顾客后剩下的需求量为0;式(23)保证需求量不超过原配送中心容量;式(24)保证配送完后不回配送中心;式(25)保证每个顾客由一个配送中心服务;式(26)~式(27)避免不可行解;式(28)~式(30)表示变量的取值;式(31)保证需求量不超过虚拟配送中心容量;式(32)~式(33)表示变量的取值。
2 低碳动态需求开放式选址—路径问题算法设计
2.1 算法求解过程
结合量子进化算法较强的全局搜索能力和差分进化算法较好的局部搜索特性,本文设计了混合量子差分进化算法(Quantum Differential Evolution algorithm, QDE)进行求解。该算法包括4个阶段:①由备选配送中心位置及顾客需求确定初始配送中心;②根据车辆容量限制形成顾客集;③将顾客集分配给配送中心;④运用量子差分进化算法进行路径优化。具体过程如图1所示。

(1)配送中心的确定
参考文献[18]的方法,按照以下过程确定初始配送中心:
1)按式(34)计算所有顾客到备选配送中心的欧氏距离:
(34)
式中:(xi,yi)为备选配送中心i的坐标;(aj,bj)为顾客j的坐标;Nc为顾客数;Nm为待选配送中心数。
2)按式(35)计算配送中心选择因子:
(35)
式中:QPi为i配送中心容量限额;Oi为i配送中心固定费用;Pi由式(34)求得。
3)将ηi由大到小排序,按总配送中心容量不低于总需求量确定配送中心个数,并按ηi排序依次选择配送中心,将其放入已选配送中心集M。
(2)车辆顾客群的确定
将贪婪算法与量子进化算法相结合确定顾客群,具体执行过程如下:

2)将α、β矩阵按式(36)转换成二进制矩阵G,式中r为均匀分布的[0,1]随机数:
(36)
将矩阵G解码成满足车辆载重的顾客集,解码过程为从G中随机选择第一个顾客i,若其满足车辆载重要求,则将i放入该车,按式(37)确定下一个配送顾客l:

(37)
若未有顾客能放入该车辆,则重新派出车辆,直到所有顾客都分配完成。
解码后用0表示车辆开始,图2为某一15个顾客的配送方案解码后的结果。由图2可知,该方案需要两辆车,第一辆车的配送顺序为“配送中心-6-2-9-4-11-13”,第二辆车为“配送中心-5-1-3-7-8-10-12-14-15”。

(3)确定服务车辆的配送中心
1)计算每辆车的重心值如式(38)所示,式中nc为车辆c中顾客数;(aj,bj)为c车中顾客的位置坐标;(a(c),b(c))为其顾客的重心位置坐标,
(38)
2)按式(34)计算每辆车与配送中心集M中所有元素的距离Wi,将Wi由小到大排列。
3)将未分配的车辆分配给其距离最短的配送中心,对不满足该配送中心容量限额的车辆,按Wi顺序依次分配到其他配送中心,直到所有车辆均分配为止。
(4)路径的优化
上述每辆车均可视为单配送中心开放式车辆路径问题(Open VRP, OVRP),本文设计量子差分进化算法进行路径优化,具体操作如下:
1)染色体编码
量子差分进化算法的染色体编码采用Q-bit的形式,这种编码方式不能直接适用于VRP,因此本文首先将Q-bit编码的染色体转换为二进制串,然后将二进制串看作随机键,最后将其转换成基于客户序列的整数编码。具体执行过程为:对于L个客户的VRP,将其每一个基因表示成长度为L的Q-bit串,这样就得到L组长度为L的量子染色体,因此一个量子染色体即可表示为一个L×L×2的两维量子比特矩阵。
2)初始化种群
随机产生多个初始种群,按上述编码方式,种群中的每个染色体为L组,每组含有L个量子比特串,量子比特各位随机初始化,即量子位概率幅α、β为[0,1]的随机数,但需满足α2=1-β2。
3)量子变异
按照差分进化算法的进化方法设计量子差分变异,选择当前种群最优解的概率幅作为父代量子概率幅,与另外两个不同解的量子概率幅进行差分运算,生成新的量子比特,具体方法为:
(39)
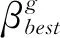
4)量子交叉
对选定的父代个体进行交叉混合(如式(40)),以产生新的多样性个体。
(40)
式中:randj为[0,1]的随机数;Cr为交叉因子,取值范围[0,1]。
5)量子更新
通过量子旋转门更新实现状态间的转移,从而引导个体进化的执行过程,本文设计如下动态量子旋转门进行状态的更新与转移:
(41)
式中:
(42)
(43)
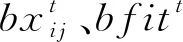
6)量子选择
应用贪婪原则进行选择种群的量子比特,具体操作如下:
(44)
式中f为适应度函数。
7)量子差分进化算法的求解流程
路径优化的执行过程如下:
步骤1初始化,令n=1,θ=θ0,α=αt,β=βt,生成初始量子比特种群Q(t)。
步骤2解码生成初始路线。
步骤3局部优化方法调整方案,若调整后,解得到改善,则替换原方案;否则不替换,计算目标函数值,保留最优个体。
步骤4判断是否满足终止条件,若满足,则输出最优解;若不满足,则转步骤5。
步骤5按式(39)~式(44)进行量子交叉、变异、更新、选择,得到新的下一代量子比特种群Q(t+1)。
步骤6t=t+1,转步骤2继续执行。
2.2 算法收敛性
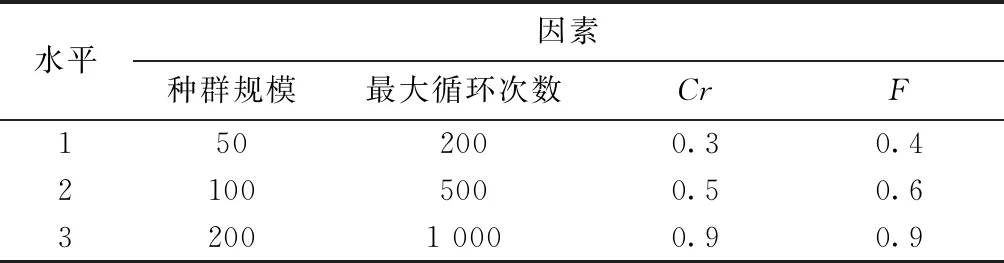
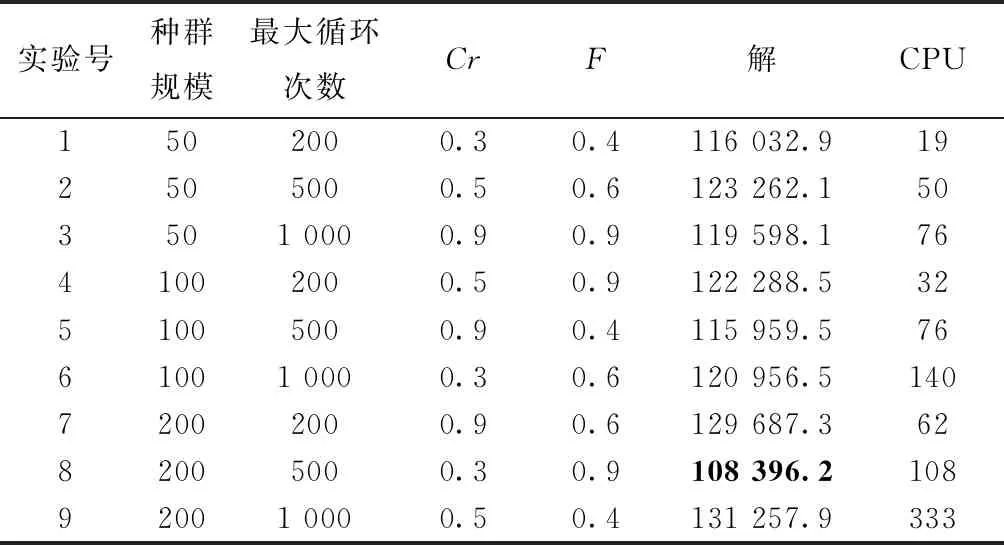
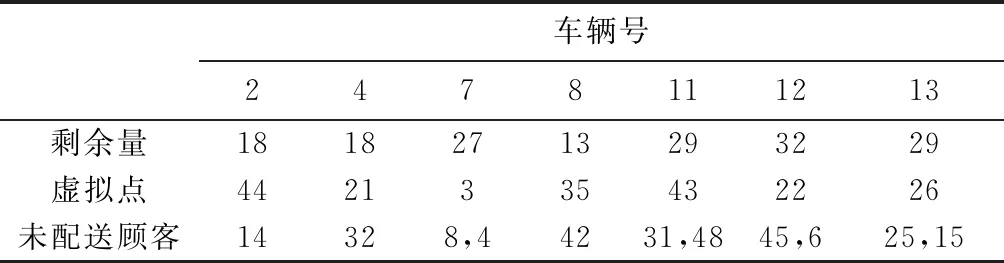
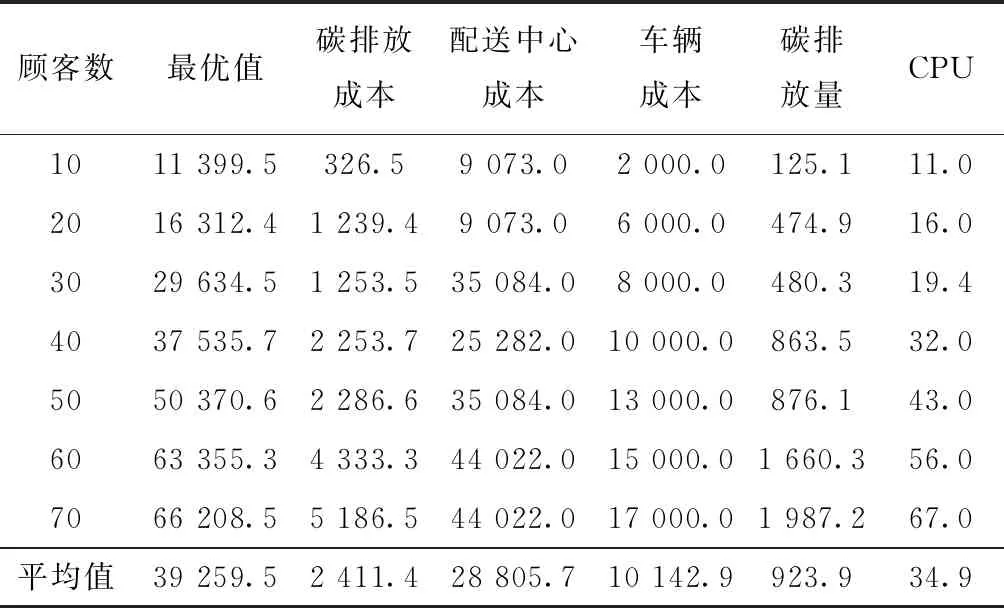
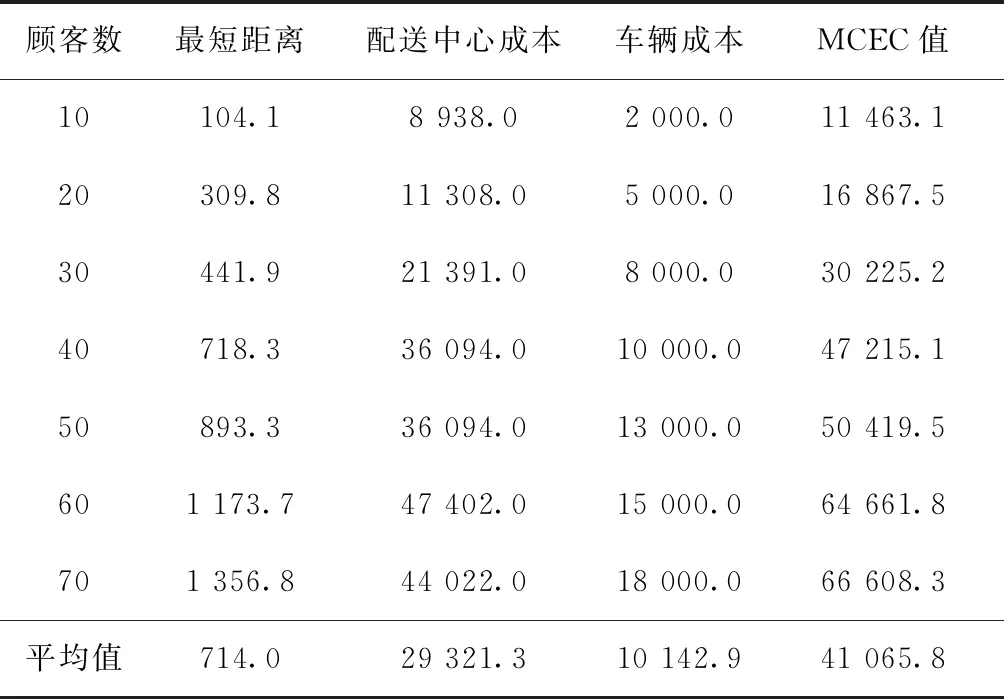
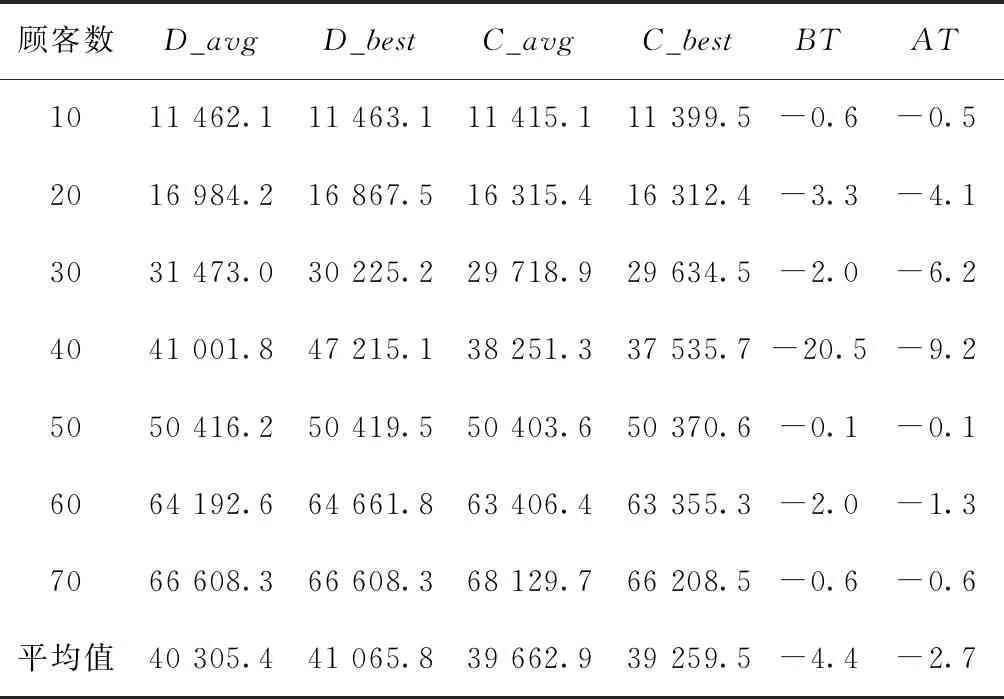
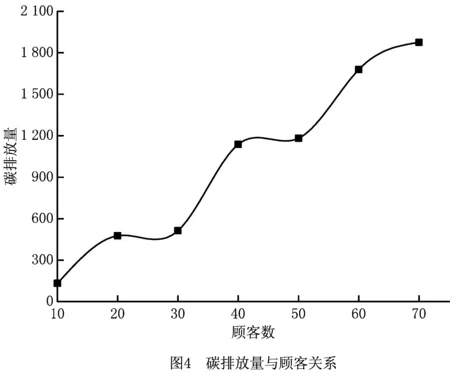
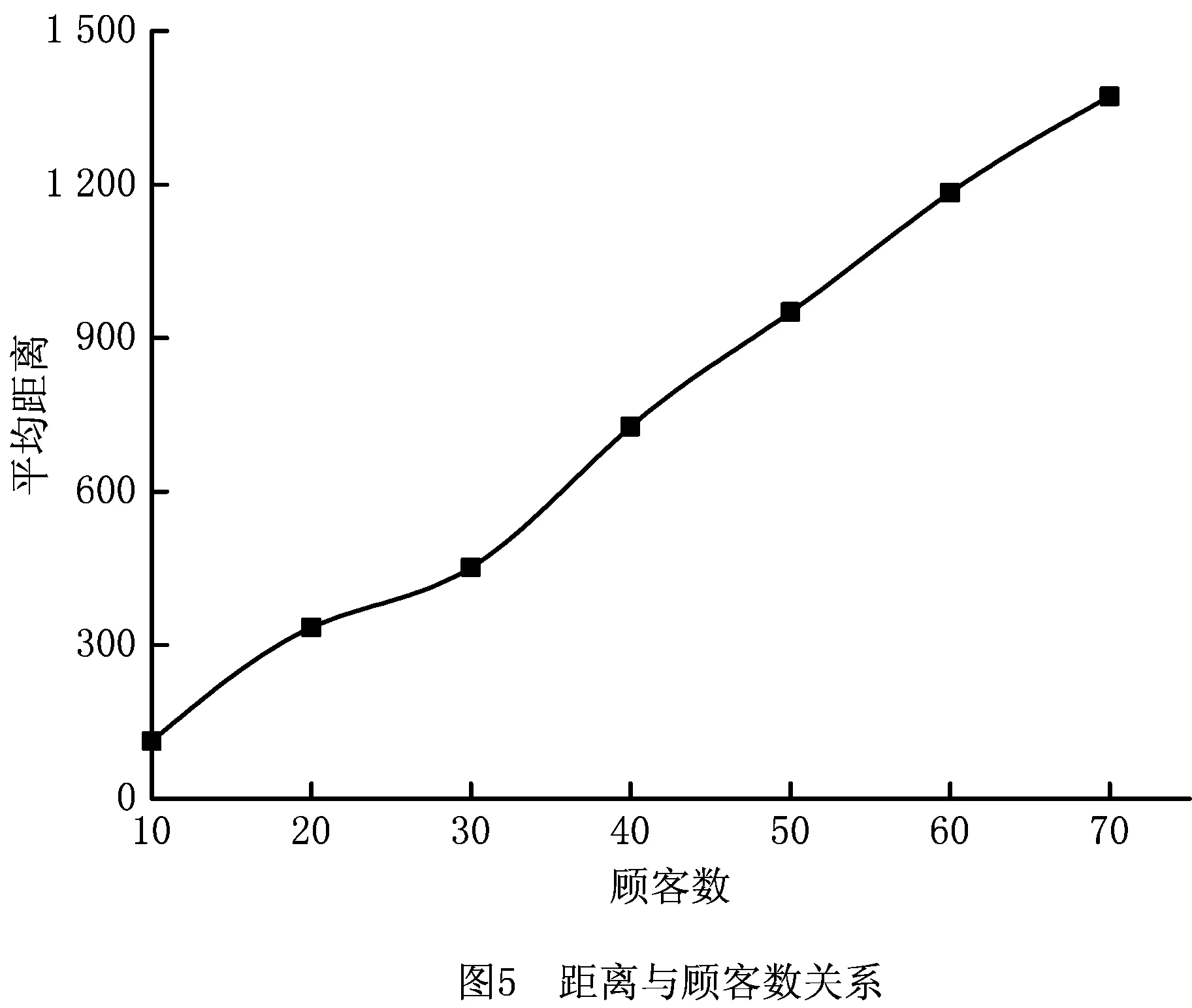
引理1在算法中,整个种群的进化方向是单调的,即满足f(xi(n+1)) 证明本文量子差分进化算法采用精英选择算子,确保种群在进化过程中较为优秀的量子个体进入下一代种群中,从而使得整个种群的进化方向是单调的。 证明假设在时刻n时,X(n)已经进入全局最优解集M,由引理1可知,在n+1时刻,X(n+1)也必然落在全局最优解集M中,即满足P{X(n+1)∈M|X(n)∈M}=1。 则 P{X(n+1)∈M}=P{X(n)∉M}· P{X(n+1)∈M|X(n)∉M}+ P{X(n)∈M}·P{X(n+1)∈M| X(n)∈M}=[1-P{X(n)∈M}]· P{X(n+1)∈M|X(n)∉M}+P{X(n)∈M}· P{X(n+1)∈M|X(n)∈M} =[1-P{X(n)∈M}]·P{X(n+1)∈M| X(n)∉M}+P{X(n)∈M}。 1-P{X(n)∈M}=1-[1-P{X(n)∈M}]· P{X(n+1)∈M|X(n)∉M}-P{X(n)∈M} =[1-P{X(n)∈M}]·[1-P{X(n+1)∈M| X(n)∉M}]≤[1-P{X(n)∈M}]·[1-g(n)] ≤[1-g(n)]*[1-g(n-1)]* [1-P{X(n-1)∈M}] … ⟹P{X(n+1)∈M}≥1- 因此,算法收敛。 混合量子差分进化算法的控制因子主要包括种群规模、最大迭代次数、缩放因子F及交叉概率Cr。为了确定最佳参数组合,采用L934正交表对Barreto算例20-5-1进行测试,如表1[16]所示为参数因素水平,实验结果如表2所示。 表1 因素水平表 表2 正交实验结果 由表2可知,种群增大或循环次数增加均可改善最优解,但也会导致计算时间增加。综合考虑解的效果及计算时间损耗,本文应用直观法选择上述实验最佳结果,即实验8的参数组合。 实例1由于OLRP无标准测试算例,参考文献[15],在[50,50]的矩阵区域随机产生50个初始顾客,顾客需求为[10,20]的随机数,配送中心及车辆数据来源于文献[17],车辆载重为70 t,其固定费用为1 000元。 求得预优化阶段的配送中心及配送路线如表3所示。由表3可知,预优化阶段选择配送中心2、4、5,其目标函数为49 040元。配送中心2负责5、7、8、9四条线路的配送任务;配送中心4负责3、11、12、13四条线路的配送任务;配送中心5负责其他5条线路的配送任务。 表3 预优化低碳动态需求LRP解 假设某一时刻检测到20个新需求,顾客坐标及需求量生成方式与预优化相同。此时,原配送中还有11个顾客没有服务,分别为顾客14、32、8、42、31、45、25、4、48、6、15,分布于2、4、7、8、11、12、13共7辆车中,车辆具体情况如表4所示。表4中的车辆号为上一阶段未服务完成的车辆编号,第3行是车辆剩余量,第4行是车辆所在的位置,第5行是该车辆在上一阶段未服务完成的顾客编号。 表4 车辆实时状态情况 计算得实时阶段的LRP结果,如表5所示。表3中第2列方框中数字表示上一阶段未配送完成顾客,第3列括号中无下划线值表示虚拟配送中心,下划线的值表示预优化阶段的配送中心。由表5可知,配送中心只需重新派出车辆2、3、4、5、6、13共6辆车即可完成所有的配送任务。 表5 实时优化路径 为进一步分析本文模型,单独响应实例1中预优化和实时两个阶段的需求,即分别按本文预优化模型进行求解,并将两阶段结果相加,此求解策略被称为IR策略,本文前述求解策略被称为RR策略,两策略求解结果如表6所示。表6中Gap由式(45)求得。由表6可知,相较于RR策略,应用IR策略求得的最优值将增加15.05%,其中碳排量将增加53.35%,因此所提出的RR策略有助于减少选址—路径的碳排放量。 (45) 实例2为进一步对本文动态策略进行实时分析,针对杭州经济开发区物美超市的实时配送服务进行了仿真,算法中顾客及配送中心位置来源于百度地图数据,随机产生10个顾客,顾客与区域内两个配送中心即物美下沙店和物美云水店的实际距离如表7所示,配送中心容量取10 000,车辆固定费用、顾客需求产生方式与实例1相同。 表7 超市与顾客距离 km 将表7数据应用于本算法,求得的配送中心选择及最佳配送路径,如图3所示。 图3中:右侧为选择物美云水店服务的顾客,其路线为4-5-2-3-1;左侧为物美下沙店服务的顾客,其路线为6-7-10-8-9,其目标函数值为22 014.55。 为分析顾客规模对碳排放及距离的影响,将本文所提的最小化碳排放成本目标模型与以最短距离为目标的模型进行对比,顾客取值范围[10,70]。为了便于描述,将本文所提最小化碳排放成本目标称为MCEC(minimum carbon emission cost),将最短距离目标称为MD(minimum distance),每个算例求解10次,表8、表9所示分别为MCEC和MD的求解结果。由表8和表9可知,随着顾客数的增加,MCEC及MD值均呈上升趋势,但MCEC对配送成本的影响高于对碳排放的影响,而MD则相反,对碳排放的影响高于对配送成本,二者对车辆成本的影响相当。 表8 MCEC目标的最优结果 表9 MD目标的最优结果 表10所示为MD的平均值及最优值与MCEC相应值的对比,表中D_avg、D_best分别为MD目标求得的平均值及最优值,C_avg、C_best分别为MCEC目标求得的平均值及最优值,BT、AT分别为两者最优值、平均值的差异百分比,其值由式(46)和式(47)求得: (46) (47) 由表10可知,MD目标的选址—路径决策并不是考虑碳排放成本最小的决策,在7个实验案例中,MCEC目标求得的平均成本值小于MD目标的平均成本值,总成本平均减少2.7%。两者的最优值对比也显示MD目标的方案使碳排放成本增加4.4%。因此,在选址—路径问题中若仅考虑距离因素,其碳排放成本将无法达到最小值。 图4和图5所示分别为顾客数与碳排放及距离的关系。由两图可知,随着需求量的增加,碳排放及总运输距离均会增大,但距离与需求量为较明显的线性关系,而碳排放量与需求量只是正相关,也说明需求量对碳排放的影响程度与对距离的影响程度不同。图5中,当顾客数为30时,其碳排放量为480.3;当顾客数为40时,碳排放量为863.5;当顾客数为50时,碳排放量为876.1;顾客数由40增长到50时,其碳排放量只增加了2.6,但其距离却增加了276.4。 为了测试算法性能,应用本算法求解标准带容量限制车辆路径问题(Capacity Vehicle Routing Problem, CVRP)测试算例,并与集合覆盖扩展节约算法(Set-Covering based Extended Savings Algorithm, SC-ESA)[17],化学反应优化(Chemical Reaction Optimization, CRO)算法[18],最近质心的K-聚类法(Kmeans for nearest centroid, KmeansFnO)[19]三种算法进行对比,算例来源于文献[20]。每个算例计算10次,种群数设为200,最大循环次数为500,比较结果如表11所示。表11中:第2列为标准结果,第3列为本算法的最优结果,第4~6列为上述3种智能优化算法求得的结果。 表11 QDE与其他3种算法的标准算例结果对比 由表11可知,本算法在顾客数为19~22的小型规模算例中均求得了与标准算例相同的解,相比较SC-ESA在同等问题25%(1/4)、KmeansFnO算法50%(2/4)的求出率,本算法在小型规模问题求解效果较好,在顾客数32~33的中型规模A算例中,本算法优于KmeansFnO但不及SC-ESA和CRO,在顾客数76的大型规模算例的求解效果不及其他3种算法。 本文将动态需求选址—路径问题分解为预优化及实时优化两个阶段,建立了基于虚拟配送中心的两阶段数学模型,并设计了混合量子差分算法进行求解。算法采用先确定配送中心再确定路线的求解策略,在路径优化阶段设计了最优量子差分策略、动态量子旋转门及贪婪选择原则相结合的方法,以实现解的全局及局域搜索。将所建低碳模型与最短距离模型进行对比,实验结果表明由最短路径求得的最优方案使碳排放平均成本增加2.7%,碳排放及距离均与顾客量成正相关,实时需求响应策略可使目标成本降低15.05%。最后,将本文算法与其他3种智能算法进行对比,结果显示本文算法在小型规模算例中优于其他算法,在大、中型规模算例中效果一般,需进一步在量子选择、量子更新方面进行改进。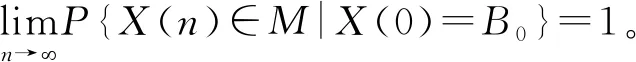



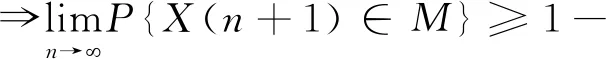
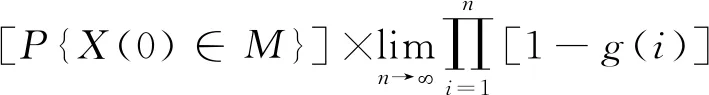
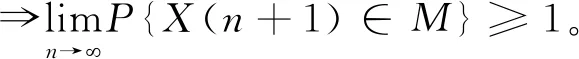
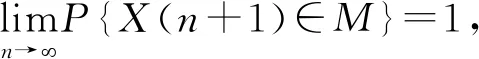
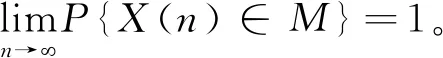
3 实验结果及分析
3.1 参数设置
3.2 实例分析





3.3 模型分析
3.4 算法测试

4 结束语

