基于正负刚度匹配原理的大行程常力微动平台设计

胡俊峰，程亮亮，张星星，李 培

(1.江西理工大学 机电工程学院，江西 赣州 341000; 2.蚌埠学院 机械与车辆工程学院，安徽 蚌埠 233030)

0 引言

常力机构(Constant Force Mechanism, CFM)是一种能在一定位移范围内提供几乎恒定输出力的机构[1-3]，也称为零刚度机构，其常力性能在精密工程、生物医疗和微纳操作等领域均有重要应用。例如，为了防止微夹持器和被夹持物接触力过大对操作对象造成损坏而设计的具有常力特性的微夹持机构[4-6]和利用常力特性进行隔振缓冲的减振装置[7-8]等。

为了实现CFM，一种方法是使用力传感器和位移传感器构建控制系统来调节机构的输出力和输出位移[9-10]，以实现机构的常力特性，但这种方法需额外搭建控制系统，结构复杂、成本较高。另一种方法是在刚性机构中使用弹簧储能结构实现常力行为[11-13]，但是由于传统运动副存在间隙、摩擦和磨损，难以应用于精度要求高的精密操作场合。目前，为了解决这个问题，一些学者利用柔顺机构[3]的弹性变形来实现常力行为。

柔顺机构是利用构件的弹性变形传递运动和力的新型机构，具有免装配、精度高、易加工和小型化、无摩擦磨损的优点[14-20]。柔性构件在力作用下会产生变形，易形成具有正刚度力学特性的结构[16-18]。而且，柔顺机构也可构成稳态结构[1]，例如双稳态梁利用其达到屈曲临界载荷后的失稳状态形成具有负刚度特性的柔性结构。因此，利用具有正负刚度的柔顺结构可设计具有零刚度特性的运动平台。目前，采用柔顺机构实现常力行为的方法有两种：①通过优化方法设计能够实现零刚度力学特性的柔顺常力结构[15-18]，包括分布式形状优化和拓扑优化，但分布式形状优化设计过程比较复杂，设计方法难度较大，拓扑优化方法得到的结构形状不规则，加工困难[2]；②利用正负刚度结构组合的方法产生零刚度机构以实现常力行为[2,17-18]。比如，文献[17-18]采用刚度组合方法设计了一种一维常力平台和二维常力平台，正刚度结构采用直梁柔性结构。但是，由于直梁柔性结构存在应力刚化效应，使得直梁柔性结构力-位移关系呈现非线性关系，这种非线性关系难以匹配双稳态梁的负刚度部分，为了满足零刚度要求，需要较复杂的结构参数设计，且会导致平台的常力范围较小。因此，为了解决常力运动平台正负刚度匹配问题，需要设计具有线性关系的正刚度结构来匹配设计零刚度运动平台。

鉴于此，本文提出一种通过设计力学特性为线性关系的正刚度结构形成零刚度结构的设计思路，分别设计了Z字型和梯形两种具有线性关系的正刚度结构，采用伪刚体方法建立了其力学模型，并通过理论分析验证了设计的可行性。将设计的两种正刚度结构与具有负刚度力学特性的双稳态梁组合搭建两种新型的常力运动平台，制作样机并与具有非线性关系的正刚度结构的常力平台进行比较分析，以说明所提出的设计思路的有效性。

1 设计原理

刚度定义为弹性元件所承受的载荷对它引起的变形的比值，可表示为

(1)

由式(1)可知，当载荷随变形增加而增加时，刚度为正；当载荷随变形增加而减少时，刚度为负；载荷不因变形增加而变化时，刚度为零。因此，零刚度结构[5]满足常力机构所需的力学特性。

利用正负刚度相抵消可产生零刚度结构，图1所示为由正刚度弹簧和负刚度弹簧并联而形成的组合弹簧，设组合弹簧在外力F作用产生的位移为d，正负刚度弹簧的刚度分别为k1和k2，则组合弹簧的刚度为

(2)

由式(2)可知，如要获得零刚度，需要将具有正刚度的结构与具有负刚度的结构并联联接。如图1所示，将正刚度结构与具有负刚度特性的结构通过连接块并联联接，使正刚度部分和负刚度部分进行抵消，从而可以得到在一定位移范围内呈现接近零刚度特性的近常力行为的机构。

负刚度结构由于采用双稳态梁结构[2]会出现屈曲现象，即随着位移增大，所施加力先增大，当到达屈曲点后开始减小，该结构具有力—位移呈线性变化的负刚度区域。目前常用的正刚度结构采用直梁结构，但该结构力—位移关系呈非线性，直梁结构和双稳态梁结构会产生如图2所示力—位移曲线。由图2可知，直梁结构所受力随位移增大而增大，呈正刚度特性，但其力—位移关系为非线性。由于非线性正刚度结构导致双稳态梁部分线性负刚度区域不能形成零刚度区域，致使负刚度区域未能得到充分利用，使得常力范围较小。因此，如果能设计具有线性关系的正刚度结构，以将双稳态梁负刚度区域尽可能多地形成零刚度区域，从而增大机构的常力范围，为设计大行程常力平台提供新的思路。

2 线性正刚度结构设计

2.1 Z字型结构

由于在横向力作用下，直柔性梁运动时轴向会产生拉伸应力，进而会发生应力刚化效应[18]。这种效应会使直柔性梁的力—位移曲线呈现非线性关系，即其刚度是变化的。为了解决该问题，在直柔性梁结构基础上增加一段柔性梁形成Z字型梁结构，如图3所示。该结构由杆1、2和3组成，通过中间梁的扭转变形来抵消拉伸变形产生的应力刚化效应。Z字型梁结构由连接块、两根对称放置的Z字型梁组成。在滑块沿竖直方向上运动时，由于中间梁会发生扭转变形，抵消了直柔性梁在轴线方向上的拉伸变形，降低轴向应力，从而减小应力刚化现象，使得Z字型梁结构的力—位移曲线呈现线性关系。

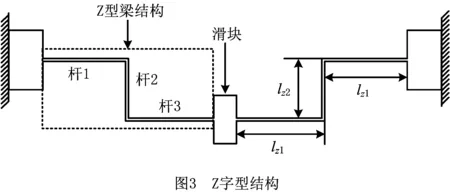
2.2 Z字型结构力学建模

由于伪刚度方法能建立反映Z字型和梯形梁结构的刚度与其结构参数之间的显示表达式，以便进行正负刚度匹配计算。下面采用伪刚度方法分析Z字型梁力—位移之间的关系，由于结构是对称的，取其一半进行分析，其伪刚体模型如图4所示。图4中，杆1和杆3的长度相同，均为lz1，杆2的长度为lz2。字母A-F表示扭簧，A、B为模拟杆1变形的等效扭簧，C、D为模拟杆2的扭簧，E、F为杆3的扭簧;θ1、θ2分别为杆1和杆2的伪刚体角;d为滑块在力F/2作用下的位移。由于杆均为固定—导向柔性梁结构，其扭簧常数可表示为[1]

(3)

式中：λ为特征半径系数，Kθ为扭簧的刚度系数，E为材料的弹性模量，I为截面惯性矩，l为杆的长度。

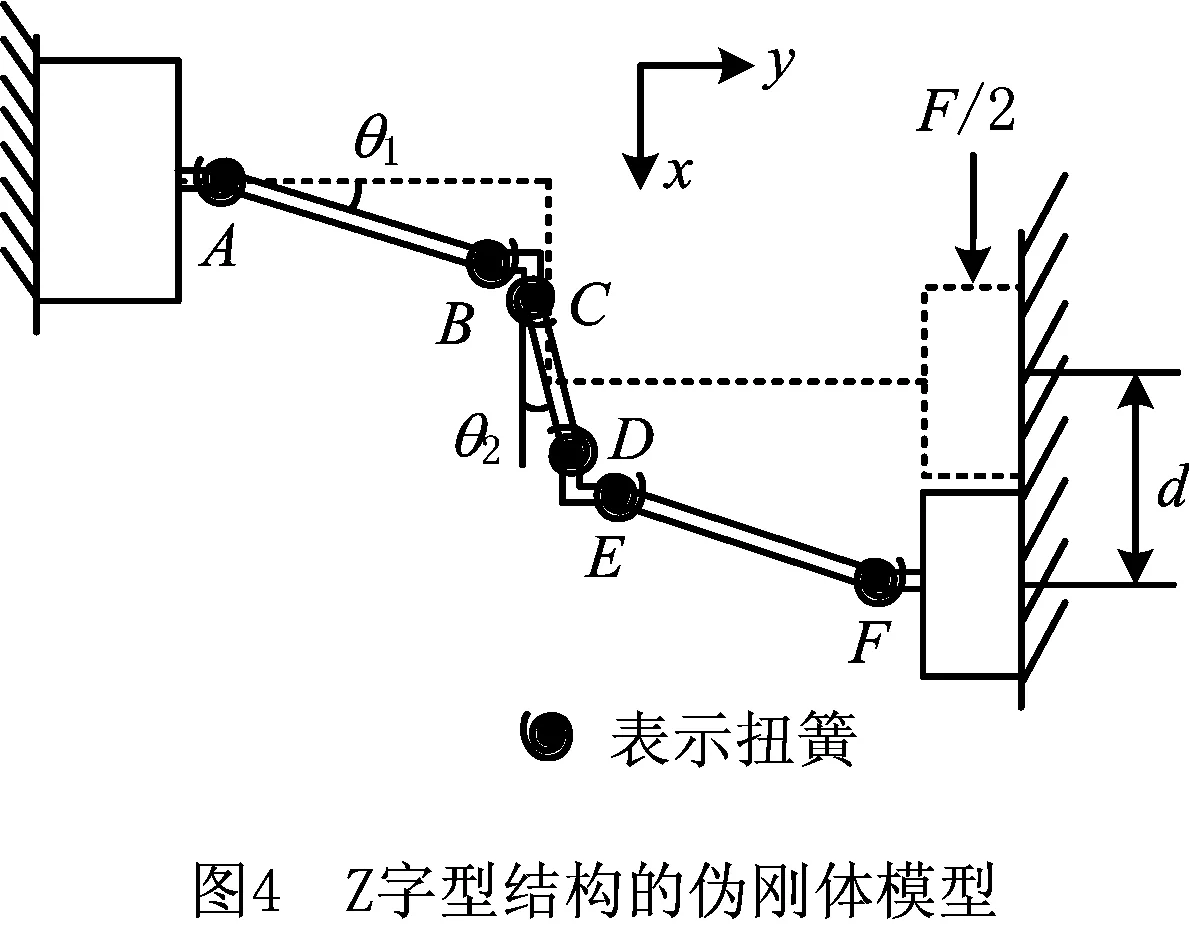
下面根据图4所示模型，采用虚功原理建立Z字型梁结构的刚度模型。

由图4可知，位移d与伪刚体角之间的关系为

d=(2λlz1sinθ1+(1-λ)lz2+λlz2cosθ2)

=2R1sinθ1-(R2-R2cosθ2)。

(4)

式中：R1=λlz1，为杆1和杆3的伪刚体杆长；R2=λlz2，为杆2的伪刚体杆长。

选取θ1为广义坐标，其虚角位移为δθ1，对式(4)进行微分可得滑块的虚位移为

(5)

滑块在力F/2作用下所做的虚功为

(6)

扭簧A、B和E、F所产生的扭矩为

T1=-κ1θ1。

(7)

式中κ1为杆1的扭簧常数。

扭簧A、B和E、F所做的虚功为

δWT1=-4κ1θ1δθ1。

(8)

扭簧C、D所产生的扭矩为

T2=-κ2θ2。

(9)

式中κ2为杆2的扭簧常数。

扭簧C、D所做的虚功为

(10)

系统总的虚功为

δW=δWF+δWT1+δWT2。

(11)

将式(6)、式(8)、式(10)代入式(11)，由虚功原理可得

(12)

由于滑块沿y方向的位移不变，可得如下几何关系:

2(R1-R1cosθ1)-R2sinθ2=0。

(13)

将式(13)对θ1求导可得

(14)

将式(14)代入式(12)可得

(15)

联立求解式(4)、式(13)和式(15)可得到Z字型梁结构的力—位移特性曲线关系，即该结构的刚度

K1=

(16)

2.3 梯形结构设计

采用Z字型梁结构减小了直柔性梁运动过程中的应力刚化效应，但未消除，增大了平台的常力运动范围。为了消除应力刚化效应，设计了如图5所示的梯形结构，由4个对称的柔性梁、2个刚性杆和2个连接块组成。在滑块运动过程中，4个柔性梁仅发生扭转变形，不会产生轴向拉伸变形，可消除应力刚化效应，使得梯形结构的力—位移曲线呈现线性关系。

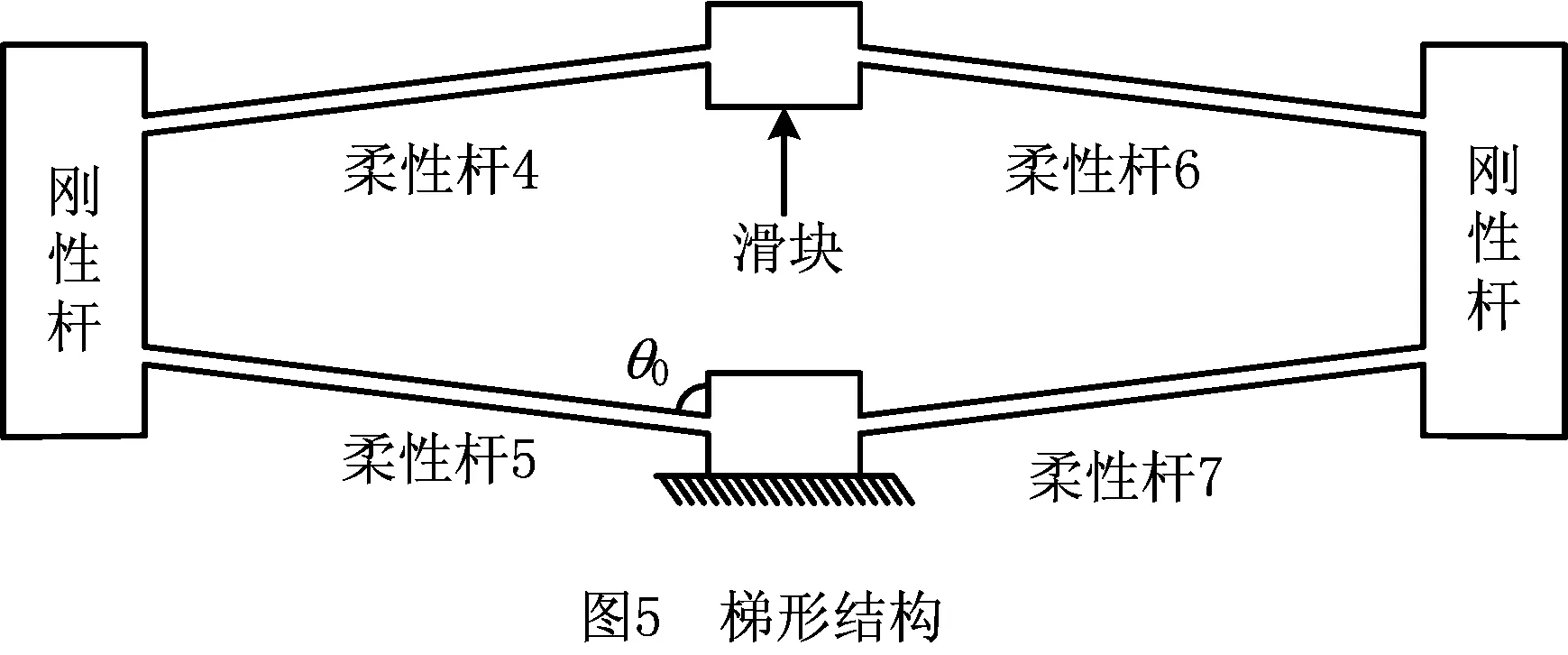
2.4 梯形结构力学模型

下面采用伪刚度方法建立梯形结构的刚度模型。由于结构的对称性在此选取一半进行力学分析，建立如图6所示伪刚体模型。图6中，柔性杆5和杆6的长度相同，均为lt。字母H-K表示扭簧，H、I为模拟杆4的变形的等效扭簧，J、K为杆5的扭簧；θ3为杆5和杆6的伪刚体角，θt为杆5与x轴的初始夹角;d为滑块在力F/2作用下的位移。

下面根据图6所示模型采用虚功原理建立梯形结构的刚度模型。

由图6可知，位移d与伪刚体角之间的关系为

d=2(R3cosθt-R3cos(θt+θ3))。

(17)

式中R3=λlt，为杆5的伪刚体杆长。

选取θ3为广义坐标，将式(17)对广义坐标θ3进行微分，则滑块的虚位移为

δd=-2R3sin(θt+θ3)δθ3。

(18)

滑块在力F/2作用下所做的虚功为

(19)

扭簧H-K所做的虚功为

δWt=-4κ3θ3δθ3。

(20)

式中κ3为杆的扭簧常数。

梯形结构总的虚功为

δW2=δWF+δWt。

(21)

由虚功原理，将式(19)和式(20)代入式(21)可得：

(22)

由式(22)可得力

(23)

当给定位移d，即可根据式(17)和式(23)可求得对应的力F，可得到梯形结构的力—位移关系，即建立其刚度

(24)

3 常力运动平台设计

根据上述所设计的两种正刚度结构和如图1所示的设计原理可设计出如图7所示的两种常力平台样机。同时，为了说明所设计的两种常力平台的优越性，加工了文献[23]所设计的直梁结构的常力平台样机，3种平台的双稳态梁结构参数相同，平台结构参数如表1所示。双稳态梁和梯形梁的初始角度分别为θd=4.5°、θt=84°。平台材料为用于3D打印的聚乳酸塑料材料，其弹性模量E为3 GPa，泊松比σ为0.3。

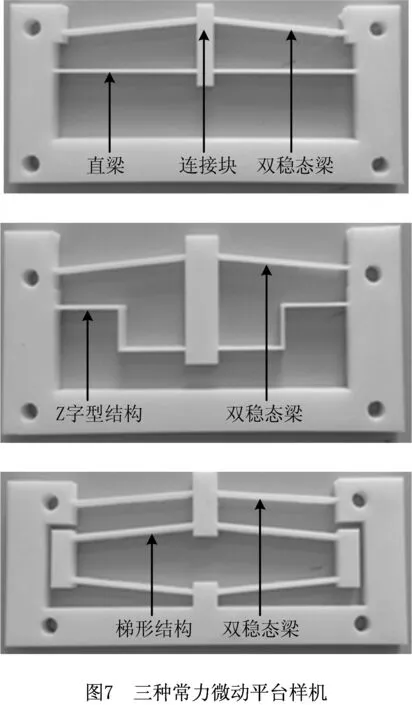
表1 平台的结构参数 mm

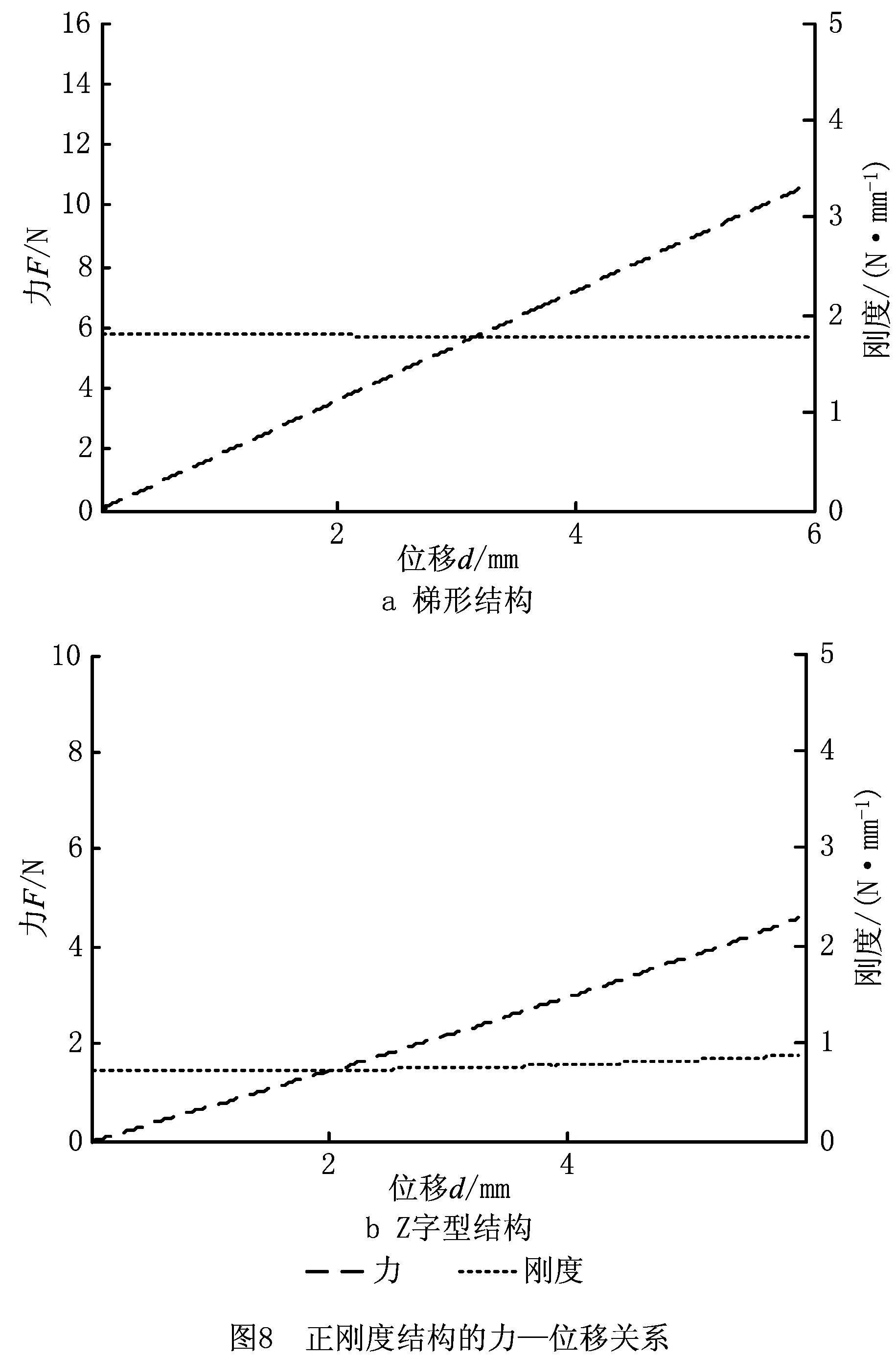
为了说明所设计的正刚度结构的力—位移为线性关系，根据上述所建立的力学模型分别可得梯形结构和Z字型梁结构的力—位移关系曲线和刚度。当两种结构的输入位移d范围为[0-6] mm时，梯形结构和Z字型结构的力—位移关系曲线和刚度变化如图8所示。由图8可知，两种结构的力—位移关系呈线性关系，刚度值几乎保持不变，表明所设计的两种正刚度结构具有恒定刚度，因此可按如下思路来设计常力运动平台：

(1)首先确定负刚度结构参数，得到该结构负刚度区域的负刚度值KN。

(2)由零刚度设计原理KP+KN=0，根据负刚度值KN得到所需的正刚度值KP。

(3)根据所需的KP和所建立的正刚度结构力学模型，确定正刚度结构参数。

根据双稳态梁理论力学模型[14]可得双稳态梁的力—位移关和刚度如图9所示。由图9可知，双稳态梁结构的负刚度KN为-1.25 N/mm，则正刚度结构的刚度应为KP=-KN=1.25 N/mm。下面根据所需的正刚度值分别来确定梯形和Z字型结构的尺寸参数。

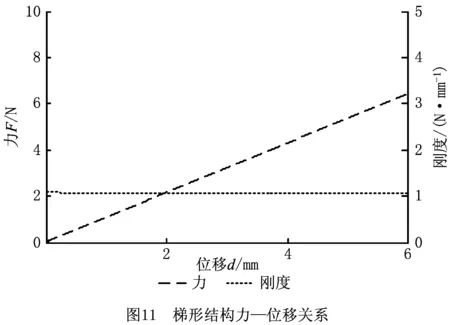
首先，确定梯形结构的结构参数。为了确定其尺寸参数，需要对梯形结构尺寸参数对其刚度的影响进行分析。设梯形结构的结构参数lt、tt、bt、θt的变化范围分别为[30～50] mm、[0.8～2.2] mm、[4～10] mm、[82°～90°]。梯形结构的刚度K2随lt、tt、bt和θt的变化曲线如图10所示。由图10可知，厚度tt、宽度bt和角度θt对梯形结构的刚度影响较小，长度lt影响较大。因此，厚度tt、宽度bt和角度θt分别设为8 mm、2.25 mm、84°，长度lt可根据所要求的正刚度值确定。由图8可知，结构刚度不随位移变化而变化，位移d=6 mm时，由式(4)可计算出伪刚体角θt=0.1 rad，则由式(16)可求得lt=50.7 mm。由该结构参数可得梯形梁结构的力—位移关系曲线如图11所示，由图11可以看出，该梯形结构的刚度约为1.25 N/mm，满足设计要求。由梯形梁结构和双稳态梁组成的平台的力—位移关系如图12所示，由图12可知，平台在[1.5～3.9] mm范围内呈现常力行为，所设计的正负刚度结构满足设计要求，说明设计思路的可行性。

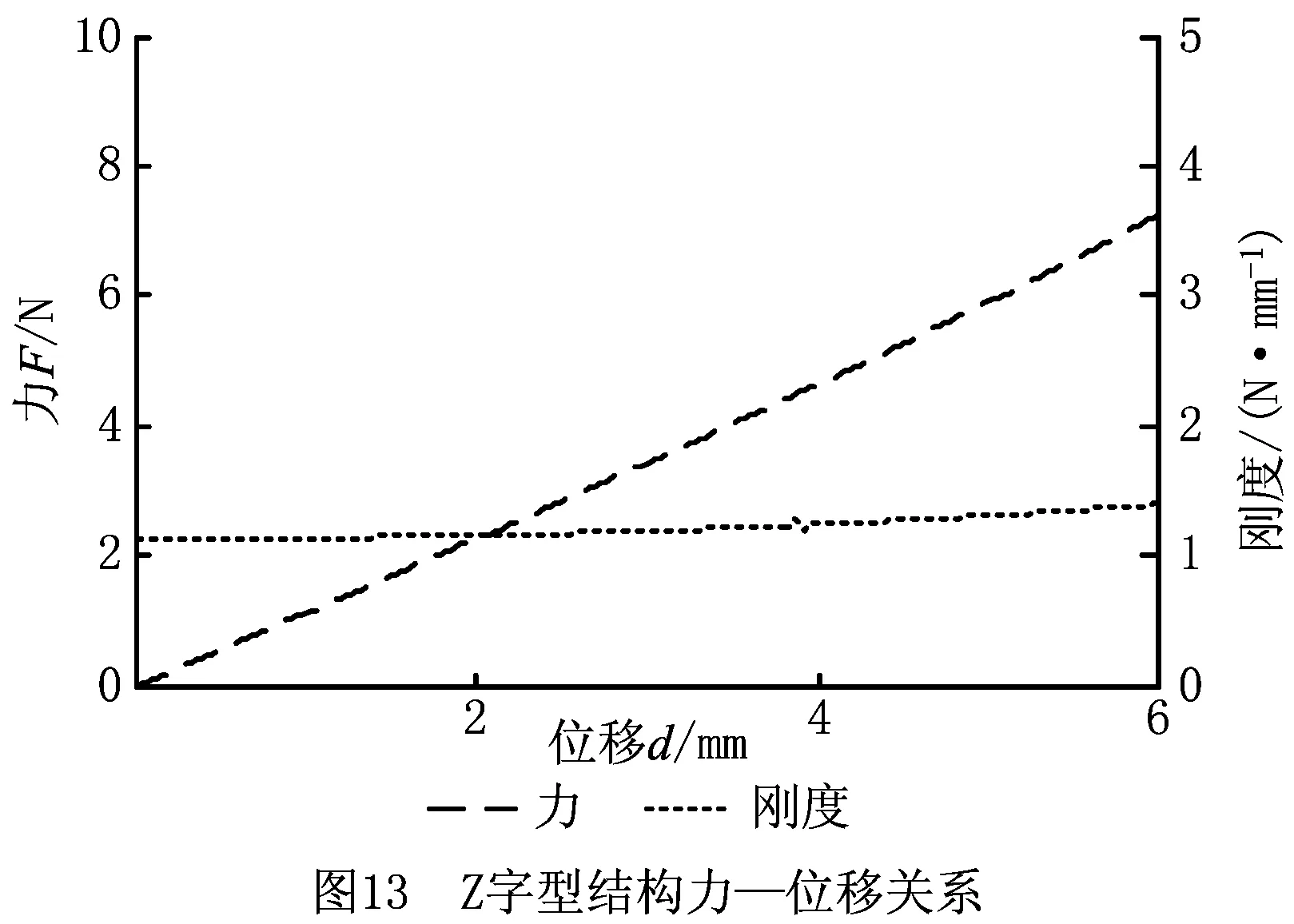
按照上述的设计思路，可设计满足所需正刚度的Z字型结构参数如表1所示。Z字型结构的力—位移曲线如图13所示，Z字型结构形成的常力平台的力—位移关系如图14所示。由图13和图14可以看出，Z字型结构平台在[1.5～3.2] mm范围内呈现常力行为，说明了设计的可行性，满足设计要求。

4 实验验证与比较分析

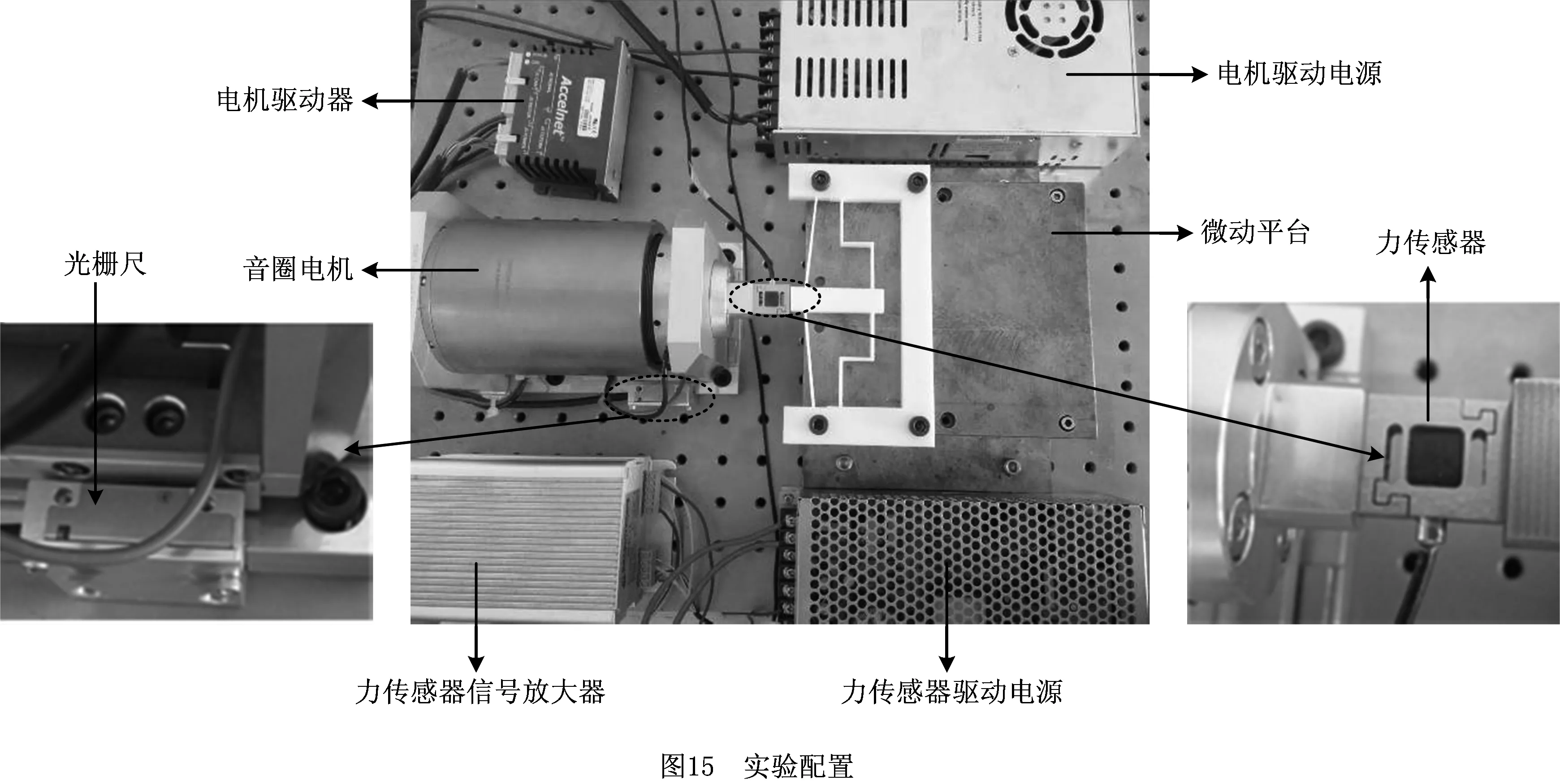
为了验证所设计常力微动平台的可行性和设计思路的有效性，搭建如图15所示的实验系统。实验测试系统由常力微动平台、音圈电机、音圈电机驱动电源，光栅位移传感器、力传感器、力传感器驱动电源、力传感器信号调理器、D/A卡、工控机组成。音圈电机为昆山同茂公司生产的型号为TMEC0400-025-000，音圈电机驱动器型号为NES-350-48，信号放大器型号为ACJ-055-18，力传感器为武汉华时呈公司生产的HS01B微小S型力传感器，量程为0-200 N，力传感器驱动电源为S-200-24开关电源，力传感器信号调理器为武汉华时呈公司的HFD-1A，D/A卡为美国NI公司生产的PCI-6713。

为了得到平台的力—位移曲线，实验过程如图16所示，用音圈电机驱动平台，对电机施加速度为10 mm/s，时间间隔为800 ms的输入信号，电机推动平台连接块产生相应位移，该位移采用光栅尺测得，对应该位移所需的推力可通过平台和音圈电机之间的力传感器测得。首先，为了说明实验测试的数据稳定性，对3个平台重复做了3次实验，实验结果如图17所示。从3次实验结果可看出，每个平台的3次实验结果几乎相同，说明平台能够提供一个稳定的常力输出和常力行程。实验所测得3个常力平台的力—位移关系理论和实验值如图18所示，由图18可知，平台的力—位移关系的实验结果与理论结果一致，说明反映常力平台力学性能的理论模型的准确性。3个常力微动平台的实验比较如图19所示，由图19可得3个平台的常力运动范围和常力值如表2所示，由表2可看出，梯形和Z字型平台较直梁平台具有较大的常力运动范围和常力值，说明了具有线性力—位移关系的梯形梁和Z字型结构能增大平台的常力范围，也说明了该设计思路的优势性。

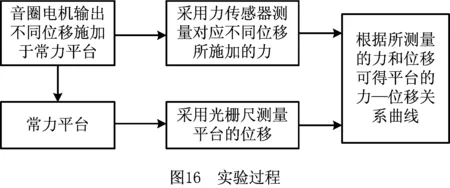
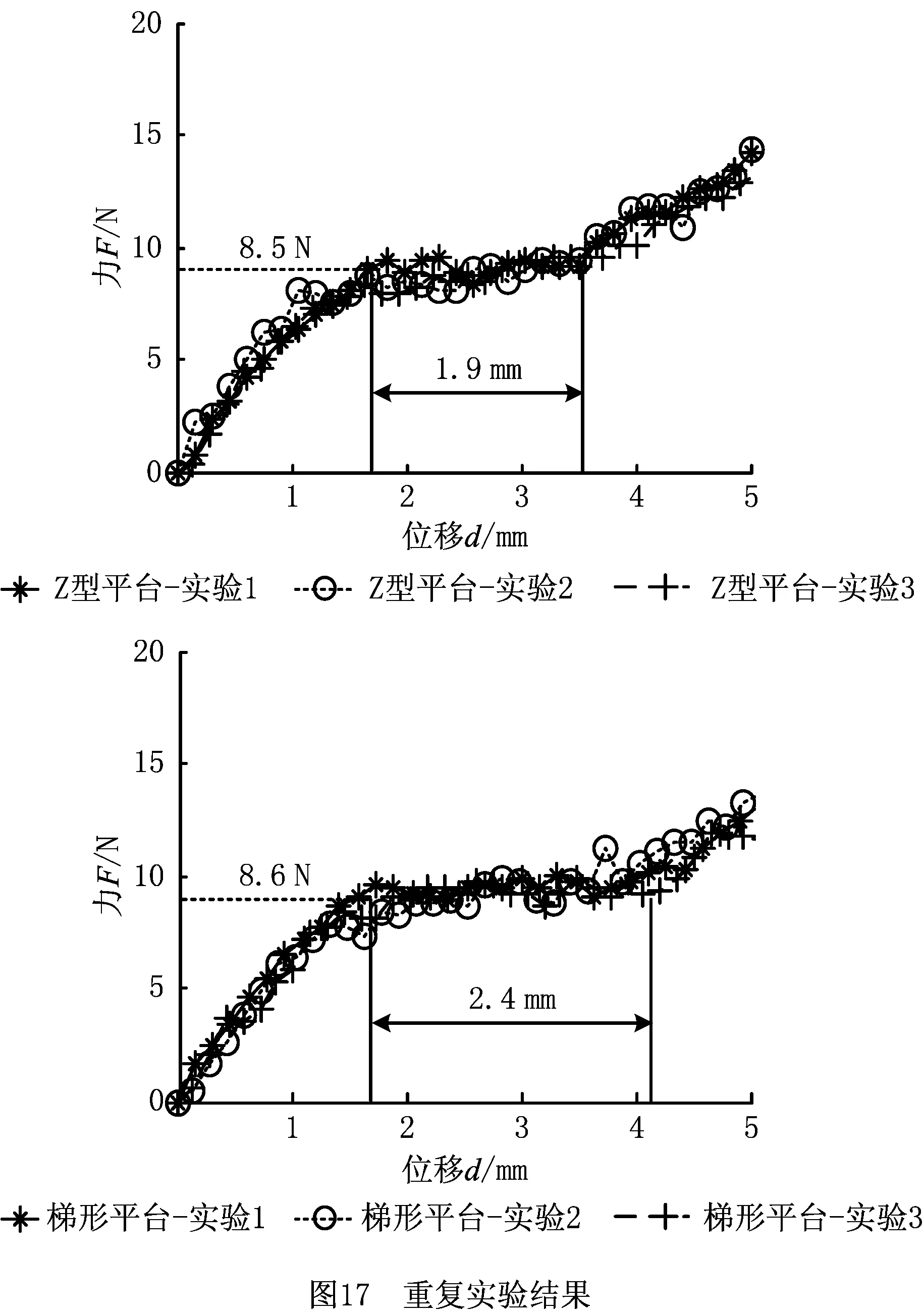
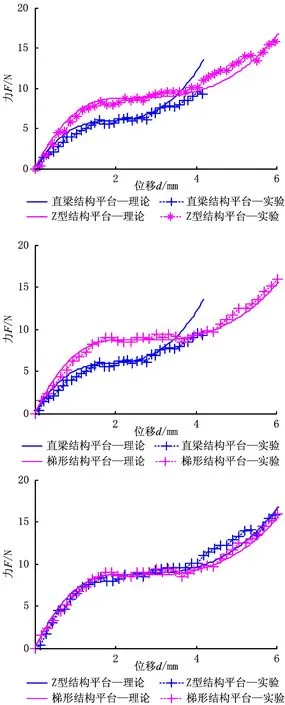
表2 三种平台的性能比较

5 结束语

为了解决常力微动平台的正负刚度匹配问题，提出一种通过设计具有线性力学关系的正刚度结构形成零刚度平台的设计思路。分别设计了Z字型和梯形两种具有线性关系的正刚度结构，采用伪刚体方法建立了其力学模型，通过理论和实验验证分析了设计的可行性。将设计的两种正刚度结构与具有负刚度力学特性的双稳态梁进行组合，构建两种新型的常力微动平台。基于正负刚度匹配原理确定了平台的结构参数，制作了样机并与具有非线性关系的正刚度结构的常力平台进行了比较分析，常力范围由1.1 mm增加到约2.4 mm，从而说明了所提出的设计思路的有效性。该设计思路可扩展应用于设计空间常力机构，下一步重点研究解决常力范围可变的问题。