基于ADALINE网络的导波载荷影响补偿方法

王熠，邱雷，袁慎芳

南京航空航天大学机械结构力学及控制国家重点实验室，江苏 南京 210016

随着航空科学技术的飞速发展，轻质、高可靠性、高机动性、高生存力及服役时间长的结构设计目标对传统飞行器的安全评定及维护保障提出了挑战，这也促进了结构健康监测（Structural Health Monitoring，SHM）技术的产生与发展[1-6]。基于导波的结构监测方法，对小损伤敏感，可实现区域监测，被视为一种很有前景的损伤监测方法[7-13]。由于结构边界条件的复杂性，导致直接分析接收信号实现损伤监测存在一定的难度，因此通常将基准信号与监测信号对比或相减，分析信号前后的差别或特征参数变化，实现对结构的损伤评估。然而导波对环境因素的变化也较为敏感，导致结构服役环境的复杂性限制了其应用。

载荷作为影响导波传播的主要因素之一。近年来，在结构健康监测领域也逐渐关注载荷对导波的影响。Michaels等在载荷影响机理上进行了较为深入的探讨，对导波在单向0～120MPa准静态载荷下的声弹性效应进行了理论分析，其研究发现当导波传播方向与载荷作用方向相同时，高频导波S0模式相速度随载荷的增大而呈线性减小，且同一载荷大小的作用下，导波在各个方向上的传播速度不同[14-16]。Amjad等通过试验方法对板结构中传播的导波受载荷影响情况进行了定量化的统计，A0模式在低频情况下，相速度随载荷增大而变快的，高频A0和S0模式的相速度是随载荷增大而变慢的[17]。Kang、Roy和Chang等学者将压电影响考虑在内，建立了压电常数d31随载荷变化的线性模型，认为导波信号幅值受载荷影响主要是由于d31的变化，飞行时间则是由于结构声弹效应引起[18-20]。邱雷等将载荷引起的声弹效应和d31变化均考虑在内，进行了载荷影响下的压电导波多物理场仿真，得到单轴拉伸载荷下的仿真结果，与试验得到的载荷影响下的速度和幅值变化结果吻合[21]。

针对导波信号补偿方法研究主要集中于温度影响，研究者们提出了包括最优基准扩展（BSS）和最优基准选择法（OBS），基于信号处理以及理论建模的补偿方法[22-25]。而针对导波的载荷补偿方法研究较少，Roy 和Chang 等在其提出的载荷影响理论模型基础上，通过单向载荷拉升试验获取实测数据来训练模型的参数，从而获得一个完整的数值参数用于后续监测中的载荷补偿[20]。卿新林等采用有限元法对压电传感器获得的结构中导波的载荷效应进行了分析，发现幅值和相位随载荷的变化是线性的，并且在此基础上，建立了一种基准信号与补偿信号之间的线性数字模型，对信号添加幅值因子与相移，并通过获得多个路径导波信号幅值相位随载荷变化的斜率，代入到其建立的数字模型中，以此对传感网络中的监测信号进行载荷补偿[26]。

综上所述，载荷对于导波的影响是显著的，目前的载荷补偿方法研究较少，已有方法需要进行理论建模且计算量大。针对上述问题，本文提出了一种基于ADALINE网络的载荷补偿方法。该方法在不需要进行载荷影响理论建模的基础上，通过构建目标载荷下导波响应信号和基准载荷下导波响应信号的数学模型，通过训练神经网络，得到基准信号附近载荷的信号补偿参数，能显著减少温度补偿所需基线，实现大范围温度的导波补偿，并且具有较高的计算效率。

1 基于ADALINE网络载荷补偿方法

1.1 补偿原理

图1 为载荷作用下的导波传播示意图，从信号与系统的角度将正逆压电效应、胶层的作用、结构的作用都考虑为传递函数。对于这样一个包含PZTA和PZTB两个传感器的激励传感通道，PZTA作用了激励电压信号Va，则相应的PZTB的响应信号在频域的表达式为：

式中：Ks(ω)和Ka(ω)分别为压电片在激励和传感过程中考虑了胶层耦合作用的电机和机电耦合系数。GAB(ω)表示导波在结构中从输入端PZTA到输出端PZTB这一过程中与应变相关的传递函数。

图1 载荷作用下的导波激励传感模型Fig.1 Guided wave excitation sensing model under load

当载荷发生变化时，Ks(ω)、Ka(ω)和GAB(ω)都会受到载荷的影响。因此得到在L1和L2载荷作用下响应信号可以分别表示为式（2）和式（3）：

则两响应信号在频域内的关系为：

由式（4）可以知道，存在一个系统，其输入为VAB(ω,L1)，输 出 为VAB(ω,L2)，传 递 函 数 为H(ω,L1,L2)。 通 过 构 建ADALINE网络模拟这样一个线性输入输出系统，通过数据库的训练来模拟载荷对导波信号的影响。训练完成后，只需要少量的基准来实现大载荷段内的补偿。

1.2 补偿流程

基于上述载荷补偿方法原理，给出了基于ADALINE网络的载荷补偿方法流程，分为以下三部分。

（1）获取数据库

在结构各受载状态下，获取导波响应信号数据库。

（2）网络训练

根据载荷补偿范围以及补偿标准进行网络训练，获得目标载荷下的网络权值，此时只需要存储少量的基准信号及网络权值。图2为ADALINE网络训练示意图，以L0载荷下的导波信号作为基准，以L0，L1，…，LN载荷下的导波信号作为参考，通过网络训练获得网络权值。

图2 ADALINE网络训练示意图Fig.2 Schematic diagram of ADALINE network training

（3）网络使用

根据实测结构受载情况，调用存储的目标载荷下的基准信号及网络权值，进行载荷补偿，获得此载荷下的基准信号。图3为ADALINE网络使用示意图，在实际监测过程中，测得结构受LN载荷，调用LN载荷对应的L0载荷下的导波信号，结合其对应的网络权值，计算得到补偿后的LN载荷对应的基准信号，与实际在LN载荷下获得的监测信号对比，实现损伤诊断。

1.3 网络参数设计

ADALINE 网络在数字信号处理领域可以看作是有限长的单位冲击响应滤波器（Finite Impulse Response，FIR），它可以在保证任意幅频特性的同时具有严格的线性相频特性，同时其单位抽样响应是有限长的，因而滤波器是稳定的系统。根据这种特性，可以用于补偿载荷变化对导波信号造成的幅值、相位变化。

图3 ADALINE网络使用示意图Fig.3 Schematic diagram of using ADALINE network

自适应滤波器ADALINE 网络的结构包含输入层和ADALINE层两层，如图4所示。输入层是由抽头延迟线构成，ADALINE 层传递函数是线性传递函数。输入信号f(t)为基准载荷下的导波信号，在抽头延迟线的输出端得到M维的矢量，包含当前时刻的输入信号和抽头延迟1 到M-1时间步长的信号，M代表抽头延迟线的阶数。

图4 自适应滤波器ADALINE网络的结构Fig.4 Structure of ADALINE network with adaptive filter

网络的输出可以表示为：

式中：a(t)为目标载荷下获得的导波信号，wm是可随载荷变化自适应调节的滤波器参数，即网络权值。将其表示为矩阵形式：

本文综合考虑训练精度以及训练效率，设计了2 阶抽头延迟线自适应滤波器ADALINE网络，即M=2。则L载荷下的基准信号经抽头延迟后为：

将另一载荷下的基准信号f(t)作为参考信号：

采用神经网络中常用的均方误差（Mean Square Error,MSE）进行ADALINE网络训练：

将式（9）写成矩阵形式：

式中：c=E[t2]为基准信号t的自相关矩阵，h=E[tzb]为网络输入输出的互相关矩阵，R=E[zbzbT]为网络输入的自相关矩阵。采用梯度法求函数F(w)的最小值，得到式（11）：

因此，如果自相关矩阵R是正定的，则将有一个唯一的驻点，并且是一个强极小点，即网络的权值可以计算为：

完成上述过程后，在实际的监测过程中，通过测得当前结构状态下所受载荷，选择与之匹配的补偿基准信号及权值矢量，即可获得补偿后当前载荷下的基准信号，结合基于导波的损伤诊断方法即可实现对结构的状态监测。

1.4 补偿精度

网络训练完成后，依然会存在一些误差，而基于导波的结构损伤诊断方法通常会用到基准与监测信号作差得到的散射信号，因此本文选择归一化最大误差作为补偿精度的标准，即参考与补偿后信号差信号最大幅值的绝对值除以参考信号的最大绝对峰值，定义：

本文通过在结构中粘贴模拟损伤，分析损伤发生前后信号的归一化误差，研究发现：当结构中没有损伤时的归一化最大误差在-30dB左右，有损伤时为-5dB左右。因此将补偿精度设置为-25dB，即补偿后精度Er ＜-25dB。

1.5 网络训练过程

基于上述对补偿网络结构参数设计，以及确定的补偿精度，得到如图5所示的基于ADALINE网络的训练过程。具体步骤如下：（1）当结构处于健康状态时，获取结构各受载状态下的基准信号；（2）选择补偿载荷范围；（3）以某一载荷下的基准信号作为网络输入，另一载荷下的基准信号作为网络输出，对网络权值进行训练；（4）通过最小均方误差进行参数优化；（5）利用获得的网络权值与输入的基准信号计算补偿后的基准信号；（6）计算补偿后的信号与参考信号的误差，若满足补偿精度存储此时的输入基准信号、权值以及载荷补偿范围，若不满足则调整补偿载荷范围重复步骤（3）。

图5 载荷补偿流程及使用Fig.5 Process and using of load condition

2 载荷补偿方法的试验验证

为验证本文提出的载荷补偿方法的有效性，在碳纤维复合材料板上，开展了载荷影响下的损伤监测试验验证，实现了大载荷段的补偿，提高了损伤诊断可靠性。

2.1 试验设置

试验选择了一块尺寸为250mm×40mm×2.2mm 的碳纤维板复合材料板，如图6 所示，在其表面粘贴了两枚压电片，压电片间距为150mm，其中PZT1用作激励压电片，PZT2用作传感，组成传感通道，两枚压电片距离上下边界为20mm、距离左右边界为50mm，如图7所示。

图6 带有压电片的碳纤维板Fig.6 Carbon fiber plate with piezoelectric transducers

图7 试件尺寸及压电片位置Fig.7 Specimen size and position of piezoelectric transducers

试验系统如图8 所示，包括用于提供载荷的拉伸机及其控制系统，用于激励采集导波信号的集成导波SHM 系统，以及一台动态应变仪。试验中采用正弦调制五波峰信号作为激励信号，振幅为±70V，其中心频率设置为60kHz，采样率设定为10MSPS。载荷范围设置为0～100MPa，步进5MPa。试验过程分为两部分：（1）在结构处于健康状态时，利用拉伸机提供各级载荷条件，在各级载荷保载状态下重复采集两次导波信号；（2）在试件中心粘贴10mm×10mm吸波材料用于模拟损伤，重复步骤（1），获取结构损伤状态下的导波信号，采集信号一次。

图8 载荷影响导波试验Fig.8 Guided wave experiment under load condition

2.2 载荷对信号的影响

图9 为不同载荷级别下的导波原始信号，对直达波峰值部分进行放大，可以看出，载荷对信号的影响是显著的，相位出现了明显的前移，且幅值变大。

为了定量分析信号随载荷的变化，图10及图11给出了信号直达波峰幅值（绝对值）以及相位统计结果，并进行了线性拟合。可以看出信号幅值随着载荷的增大而增大，相位则是减小，且两特征参数随着载荷的增大基本呈线性变化。

表1给出了线性拟合优度及拟合斜率。幅值变化率为1mV·MPa-1，相位变化率为-5.57×10-5ms·MPa-1，变化均较大。表中还给出了两种参数的线性拟合优度，其中信号幅值拟合优度大于0.96，信号相位的拟合优度大于0.98，表明信号特征与载荷之间存在较好的线性关系。

2.3 载荷补偿结果

本节将基于自适应滤波器ADALINE 网络的载荷补偿方法，应用于复合材料平板上进行导波信号的载荷补偿。

图12 为以50MPa 应力下的导波信号直达波段作为网络输入，其余载荷下的导波信号作为参考，得到的补偿信号与参考信号的归一化误差值，可以看出在没有进行补偿时，归一化最大误差均大于补偿精度-25dB，经过补偿后的误差 40MPa、45MPa、55MPa 以及 60MPa 下的误差均小于-25dB。由此将载荷补偿范围设置为20MPa。

图9 不同载荷下的导波信号Fig.9 Guided wave signals under different load condition

图10 载荷对信号幅值的影响Fig.10 The influence of load on signal amplitude

图11 载荷对信号相位的影响Fig.11 The influence of load on signal phase

为验证载荷补偿范围设置的合理性，分别以10MPa、30MPa、50MPa、70MPa 以及 90MPa 为网络输入，对其余载荷下的导波信号进行补偿，补偿后的归一化最大误差如图13所示。可以看出，0～100MPa下的信号均得到补偿，且经过补偿后，所有载荷下的补偿误差均小于-25dB，表明补偿载荷范围设置是合理的。

表1 特征参数拟合结果Table 1 Results of characteristic parameter fitting

图12 用50MPa信号补偿0～100MPa信号补偿误差Fig.12 Compensation error of signals under 0～100MPa using 50MPa signals

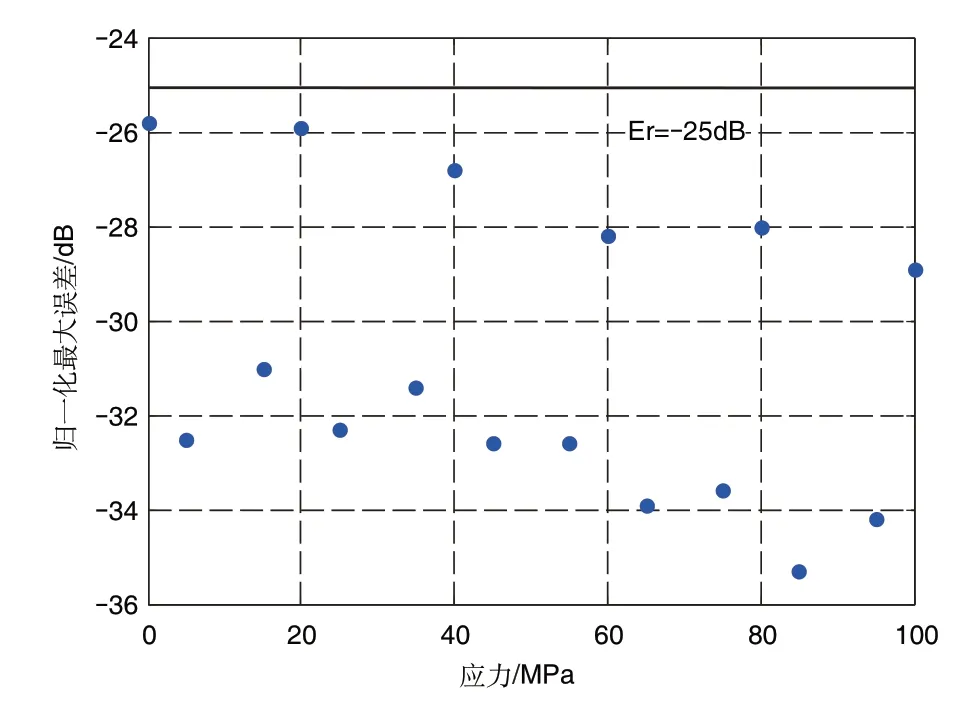
图13 确定补偿范围后0～100MPa信号补偿误差Fig.13 Compensation error of singals under 0～100MPa after determining compensation range

以60MPa 下获得的导波信号为例，如图14 所示，相比于结构未受载荷时，信号差别较大，差信号幅值接近2V。若结构在此受载状态下产生损伤，再以结构未受载时的信号作为基准，用于损伤监测，必然会产生较大误差。

图15 为将50MPa 下的信号补偿到60MPa 后得到的补偿信号，可以看出与实际获得的60MPa下的基准信号差别较小，且作差得到的差信号幅值仅0.05V 左右。若以此时的补偿信号作为基准用于损伤诊断，能有效提高损伤诊断精度。

图14 0MPa与60MPa下信号对比Fig.14 Comparison of signals under 0MPa and 60MPa

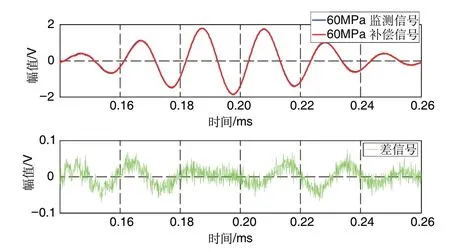
图15 60MPa下监测与补偿后的信号对比Fig.15 Comparison of signals between monitoring and compensation under 60MPa

2.4 载荷补偿方法用于损伤诊断

本节为了验证本文提出的载荷补偿方法的有效性，与基于损伤因子的损伤诊断方法结合，实现碳纤维复合材料受载状态下的损伤评估。损伤因子选用反映信号之间相关性的互相关损伤因子，计算方法如式（14）所示：

式中：H(t)为健康信号；D(t)为损伤信号；t1，t2分别为信号截取起始和截止时间。

图16为在未对信号进行补偿，直接以结构未受载状态下的信号为基准，提取损伤因子的结果，可以看出在载荷为10～50MPa区间时，损伤因子小于损伤阈值0.1，则应判别结构未发生损伤，而此时结构中已经有损伤产生，表明载荷的存在导致了损伤误判。而在应用了本文提出的载荷补偿方法后，利用补偿得到的各级载荷下的基准信号提取损伤因子结果如图17所示，可以发现在载荷为0～100MPa的区间，损伤因子均大于0.1，判别此时结构有损伤产生，实现了对结构中的损伤监测。

图16 没有补偿的损伤监测结果Fig.16 Damage monitoring result without compensation

图17 补偿后损伤监测结果Fig.17 Damage monitoring result with compensation

3 结论

本文针对载荷对导波的影响，对基于导波的结构健康监测技术带来不确定性问题，建立了基于ADALINE 网络的载荷补偿方法，研究了方法基本原理及补偿流程，并对网络参数进行设计，最后在碳纤维复合材料结构上进行了试验验证。得到以下结论：

（1）本文方法能有效实现载荷补偿，补偿范围0～100MPa，补偿间隔20MPa，且补偿后误差小于-25dB。

（2）将载荷补偿方法与基于损伤因子的损伤诊断方法结合，实现了对结构在载荷影响下的损伤诊断，提高了损伤监测可靠性。