基于改进失效模式与后果分析的制造执行系统风险分析模型

尤建新，邓晴文

（同济大学经济与管理学院，上海200092）

随着工业4.0的提出，全球迎来智能制造革命浪潮；新一代信息技术兴起，物联网、大数据与工业技术加速融合，促进了工厂生产线向数字化转型，传统制造业受到巨大影响。中国于2015年提出了《中国制造2025》战略规划［1］，大力扶持制造企业推进智能转型。在这一战略中，核心思想为信息化与工业化的融合，也就是“互联网+智能制造”。为实现这一目标，传统制造型企业转型为数字化工厂，其核心则是制造执行系统（manufacturing execution system，MES）［2］。

MES是一套面向车间执行层的生产信息管理系统，为制造企业信息化的重要组成部分。与其他信息管理系统相比，其具有系统集成难度大、涉及技术多等特点。它牵涉到计划排程、生产制造管理、库存物料管理、人员设备管理等诸多相互独立模块，并且在这些模块之间实时共享数据，将企业信息系统连接在一起，使数据能够在企业计划管理层和控制执行层之间流通［3］。系统本身的复杂性和项目开发周期长决定了其风险管理的难度较大，且MES对智能制造有重要意义，非常具有研究价值。

1 相关研究综述

1.1 MES系统风险评价研究方法

在信息化与智能化相结合的发展形势下，国内外学者开始对MES、企业资源计划（enterprise resource planning，ERP）等信息管理系统的开发和实施过程中的风险管理问题进行研究。Chitrasen等［4］通过问卷调查对软件项目风险分析建立结构化模型，将风险因子分为自发性、依赖性、联动性和独立性四类。Knowles等［5］在工业控制系统安全指标研究中，引入了“功能保障”概念来评估故障安全和网络安全。李信桂［6］采用工作分解结构法对MES项目的功能结构和风险因素进行拆分，构建风险分解结构耦合矩阵以全面识别项目风险。然而，上述研究主要从方法论的角度对信息系统项目的风险进行分类和定性评估，缺乏量化的风险排序。王东［7］将传统失效模式与后果分析（failure mode and effects analysis，FMEA）技术运用到IT项目的风险管理中，总结出项目各阶段的失效模式并由专家确认优先级。然而传统FMEA受专家水平和经验影响较大，带有一定的主观性。本文旨在提出一种更具客观性和精确性的MES风险评价方法，帮助数字化工厂识别系统主要风险及风险产生的原因，并提供风险管控策略。

1.2 FMEA研究述评

FMEA被广泛应用于企业质量管理与风险分析中，能有效提高产品、过程和服务的可靠性。传统FMEA对故障的严重度S（severity）、发生度O（occurrence）和检测度D（detection）进行评分，通过三者相乘计算风险优先数（risk priority number，RPN）［8］，从而对失效模式进行排序。然而传统FMEA存在诸多缺陷，如：评估风险因子只能通过精确值评价；计算RPN未考虑风险因子间的权重；相同RPN值的故障风险可能不同［9］。

为解决上述缺陷，许多学者将FMEA与其他方法结合起来，以弥补FMEA的不足。Reza等［10］、Bao等［11］通过将FMEA和模糊层次分析法（analytic hierarchy process，AHP）结合，得到评估指标权重，然而该方法在构建专家评估矩阵时，专家经验的差异性会对评估结果产生影响。Ji等［12］在多准则决策问题中引入模糊熵权法，将模糊集中呈现的不确定性量化，避免对权重的主观影响，以更客观的方式评估多标准决策问题。但是，熵值越大、越无序的指标不一定是风险等级最高的指标，仅用熵权法确定权重不一定能得到最合理的结果。此外，一些学者提出决策制定试验与评估实验室法（decision makingtrial and evaluation laboratory，DEMATEL）［13］、逼近理想排序法（technique for order preference by similarity to ideal solution，TOPSIS）［14］和灰色关联分析（grey relational analysis，GRA）［15］等，能更精确地确定失效模式风险水平。

本文提出了一种基于组合权重和GRA方法的改进FMEA风险分析模型。首先，借助模糊集理论对MES所涉及的失效模式分别从S、O、D三方面进行分析，并给出其等级描述，构造了各因素所对应评判集的隶属度矩阵，使用AHP对权重进行赋值，再通过熵权法中的差异化系数对AHP赋值进行调节，然后采用GRA方法进一步提高风险排序精度，进而判定MES失效模式风险排序。组合权重与GRA相结合充分利用了各指标的全部信息，有效克服了传统RPN计算方法的弊端。

2 改进FMEA模型构建

2.1 模糊评价语言集

由于专家评估中存在不确定性，使用模糊评价能更好地表达专家的偏好信息［16］。对风险失效模式的S、O和D采用7粒度模糊评价语言集，粒度的选取参考李克特量表（Likert scale），一般为5、7、9。选取7粒度是由于其比5更精确，比9更简便。各种模糊评价术语的含义如表1所示，评价标准与对应的三角模糊数(ak，bk，ck)如表2所示［17］。

采用均值面积法对三角模糊数进行去模糊化，即假设有l个专家，第k个专家权重为βk，加权平均得到专家综合评价值，其中

假设分析系统有m个失效模式，n个风险因子，相 应 的 各 指 标 值 为 pij(i=1，2，…，m；j=1，2，…，n)，则专家评价矩阵为P=(pij)m×n.

表1 各种评价语言术语的含义Tab.1 Meaning of various evaluation linguistic terms

表2 评价语言标准及其对应的三角模糊数Tab.2 Evaluation criteria of FMEA and corresponding triangular fuzzy number

2.2 风险因子组合权重

2.2.1 层次分析法计算风险因子主观权重

FMEA小组对三个风险因子S、O、D进行比较并建立判断矩阵，对于第k个专家的判断矩阵，有Zk=(zij)3×3。其中zij表示S、O、D之间的比较数值。然后检验判断矩阵一致性。检验过程如下：通过判断矩阵的最大特征值λmax求出一致性指标CI，

引入随机一致性指标RI，

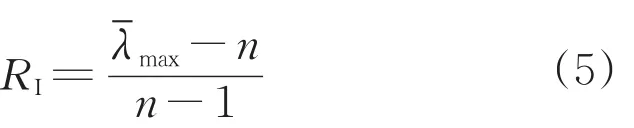
将判断矩阵中的各元素按列进行归一化处理，即

求得各风险因子主观权重值为

由此得到主观权重列向量wS=(wS1，wS2，wS3)T。

2.2.2 熵权法计算风险因子客观权重

熵权法是根据同一指标观测值的差异度对指标进行赋权，观测值差异越大则指标权重越大，即熵权法完全取决于观测值数据，是一种客观赋权法［19］。具体计算过程如下。

对评价矩阵的每个元素采用下式标准化：

式中：ej为第j个风险因子的熵。

定义差异系数gj，有gj=1-ej，gj越大表示指标越重要，并计算客观权重为

2.2.3 风险因子综合权重

在熵权法中，当重要性指标差异性较小、非重要性指标差异性较大时，可能出现重要性指标权重较小而非重要性指标权重较大的不合理现象。为减少这种情况的发生，本文先用AHP法进行赋值，保证重要性指标的权重，再采用差异化系数gj对指标权重进行调节。这样既保证重要性指标所占权重，又中和了权重的主观性和客观性，得到更精确合理的指标权重。

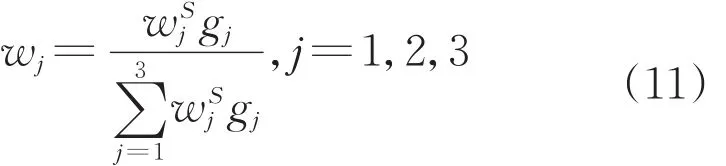
2.3 灰色关联分析

GRA方法是对系统变化趋势的定量描述方法。其基本思想是根据问题的实际背景，找出比较数据列和参考数据列的几何形状相似度，以判断其联系是否紧密。它反映了曲线之间的关联程度，通过关联度的大小确定问题的最优方案和优劣排序。其具体计算步骤如下。

步骤1：建立参考矩阵和比较矩阵。

第i个失效模式的比较数据列xi(t)(t=1，2，3；i=1，2，…，m)表示专家对三个风险因子的评价，即

从MES可靠性角度考虑，将选择失效模式评价值的最差值作为参考矩阵。针对S、O、D三个风险因子，参考数据列为：

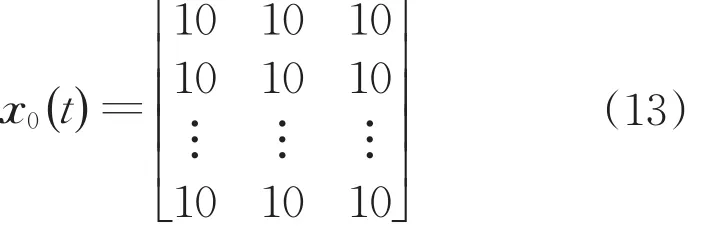
步骤2：计算灰色关联系数。

根据灰色关联理论，比较数据列与参考数据列之间的灰色关联系数可用下式求出：

式中：ζ为分辨系数，ζ∈(0，1)。

步骤3：计算灰色关联度。

在衡量失效模式排序时，各变量的影响程度不同，第i个失效模式的关联度为

步骤4：对失效模式进行排序。

根据失效模式的关联度，从大到小确定风险排序，从而有针对性地制定改进措施。

3 案例研究

H公司是一家汽车零部件制造企业。近年来，该公司正大力开展数字化工厂建设工作。现H公司将在某个分厂实施MES，并计划在该试验成功的基础上将其推广到整个工厂。因此，识别、评估和控制该分厂MES的风险因素对企业信息化建设具有十分重要的意义。

3.1 找出重点失效分析对象并分析失效模式

为准确选取风险指标，本文根据以往文献以及对数字化制造专家访谈，认为MES在管理与技术方面均存在风险。管理方面包括人力与沟通等；技术方面包括系统的可扩展性，稳定性和满足高并发和大数据量等，由此发掘出MES潜在的失效模式。根据FMEA分析方法确定重点失效分析对象及失效模式的后果及原因，结果如表3所示。

根据失效模式内容，从H公司选取出4位专家参与评价，并基于专家的专业和经验分别赋予权重β1=0.3，β2=0.3，β3=0.2，β4=0.2。利用表1的7粒度模糊语言术语集，4位专家的评价结果如表4所示。

3.2 确定风险排序

专家对三个风险因子的相对重要度进行评价，采用AHP法赋予S、O、D主观权重，风险因子判断矩阵如表5所示。

利用式（4）、（5）对判断矩阵进行一致性检验，结果如表6所示，均通过检验。

表5 风险因子判断矩阵Tab.5 Matrix of risk index judgment

利用式（6）、（7）进行归一化处理，并加权得到主观权重值，专家评价的主观权重为wS=(0.4900，0.2698，0.2402)T。

通过式（8）、（10）计算客观权重值，计算结果为wO=(0.2115，0.4365，0.3521)T。

通过式（11）可得到风险因子综合权重为W=(0.3387，0.3849，0.2764)T。

假定分辨系数ζ=0.5，根据公式（14）得到灰色关联矩阵，通过公式（15）加权得到灰色关联度ξ(x0(t)，xi(t))。根据关联度对失效模式风险排序，同时将仅用主观权重得到的排序与传统FMEA风险排序进行对比，如表7所示。

表6 一致性检验结果Tab.6 Results of consistency test and weights of risk index

表7 FMEA对比Tab.7 Comparison of FMEA

3.3 对风险排序进行分析

通过算例应用和比较可以看到，传统FMEA评价精度最低，且极易产生相同评价排序。AHP改进和综合改进后评价精度相同，结果略有差异。比如自然灾害在仅用主观权重改进的排名中为第2，是由于wS中的S权重远高于O和D，使用熵权法调整后，减小了三者差距，且由于O评价时差异性较大，综合评价认为O略高于S，而D权重相对较低。因此，该失效模式的风险排序降为4。为验证改进是否有效，将结果与往期失效数据对比，发现该评价结果与实际相吻合。由此可见，改进后的方法能够综合比较风险较大的失效模式。

融入了模糊集和GRA的改进模型更精确。在传统FMEA中不同的风险因子产生了相同的RPN，导致排序相同，无法进行比较。而引入模糊集和GRA后进一步提高精度，增加风险判断的准确性。

3.4 对故障进行分析并改善

由表7的分析结果可知，企业需求反复变更的关联度最高，是需要重点防控的对象。在MES开发、使用和发展过程中，需求也在不断地发展和变化，例如生产设备升级、原始工艺改进、增加新客户等都会导致需求的变化。变更内容主要涉及增加或减少功能模块、修改漏洞等。需求变更无法在MES项目开始时识别到，因此时间越长该失效的风险越高，会导致系统无法及时满足企业需求。为了控制该类失效模式，需要建立需求变更的生命周期模型，制定需求变更管理措施。

排在第二的失效是数据采集不准确。数据的准确性直接表明系统运行是否有效。造成该风险的原因为员工维护数据有误与仪器自动采集数据延迟。针对这两种原因，可采取的控制措施分别为增加人工录入数据防呆防错功能和引进先进的物联网技术保障采集过程稳定性。

系统运行不稳定的关联度也较高，应加强软件和硬件的维护，定期指派专人检查软硬件运行状况。自然灾害导致的事故风险排序第四。自然灾害会损害系统服务器及硬件，造成巨大损失；然而该风险不可控。然后是物料清单不准确风险。物料清单不准确一般是由于系统操作手册不够详细或工艺人员未严格执行导致的。故应加强MES操作手册规范性，同时组织专家评审。

4 结论

本文基于FMEA构建了MES风险分析模型。运用组合权重法和GRA方法对数字化工厂MES的失效模式进行分析，帮助企业明确系统运行中影响最大的失效模式。将AHP法和熵权法相结合获得风险指标综合赋权，既保证重要性指标所占权重，又减少了AHP的主观性和片面性。同时，采用GRA方法进一步提高了失效模式排序的精度，克服了传统RPN方法的不足，优化了FMEA模型，从而得到更精确、可靠的风险排序。由于MES本身系统复杂，项目开发周期长，结合FMEA事先预警的作用分析故障原因，能够更有针对性地采取措施提高系统安全性与稳定性。

FMEA不仅有助于识别MES存在的潜在风险，而且能直观具体地评价风险的大小，比较出高危失效模式，让管理者更有针对性地进行密切监控，达到防患于未然的目的。本文提出的改进FMEA模型能够更精确地分析MES的风险问题，有效预防和及时解决MES故障，对于企业信息化建设具有重大意义。