典型北方热电系统稳态功率分布计算的研究

刘梦婷，高 阳，李雯雯，戴 菁，赵志刚

（1.沈阳工程学院a.研究生部；b.科技处；c.电力学院，辽宁 沈阳 110136；2.沈阳农业大学信电学院，辽宁 沈阳 110866；3.国网辽宁省电力有限公司 沈阳供电公司，辽宁 沈阳 110000）

能源开发与使用是重要的世界性问题，随着化石能源的逐步枯竭，加之其带来的污染日益严重，对于新能源的开发和利用成为国际瞩目的问题［1-2］。基于可再生能源以及智能电网在能源革新中逐步发展的趋势，可以预见到各种形式的能源综合利用将成为未来能源领域的发展方向。

在以往的研究中，电力系统模型的研究数量较多，层次较丰富，而热力模型的研究领域略为单薄。文献［3］对于建模提出了一些建议，但由于热网的强动态特性，对模型的复杂度要求较高，简单的模型并不能很好地反映系统的实际状况，仿真程度不高。文献［4］提出了一种针对城市供水管网水压的实时监测系统，并采用粒子群优化方法对监测点的位置进行优化，但是依然存在局限性，因为热网的热损失问题并未被充分考虑，这与实际情况有差异，造成了模型精度的不足。文献［5-6］基于内点法和离散粒子群优化（DPSO），提出了一种新的电力系统无功优化混合方法，该方法将遗传与内点良好结合，分析了离散优化和连续优化，交替求解以寻求更高的全局最优效率。

综上所述，鉴于西北、华北和东北地区电热负荷严重耦合，针对该区域内特殊的供电结构，以往的电热联合优化方法已经无法满足要求。因此，优化热电机组、电锅炉、热泵等电热耦合设备，促进电力热力网络耦合发展，可以使得热电联供优化具有良好的途径及发展前景。

1 耦合能量网络中相关设备稳态模型

1.1 典型热电联供机组的电热耦合过程

典型的电力热力耦合能源网络是指在电网和热力网络的发送端和接收端耦合的能源网络［7］。煤燃烧所释放出的热能一部分用于加热锅炉中的水，产生过热蒸汽（压强为P1，温度为T1），而另一部分则在锅炉运行的各个环节中丢失（如烟气或炉渣排放）。水蒸气驱动背压式汽轮机发电（电压为V1），乏汽通过管道输送至需要热蒸汽的用户（本文以阜新热电厂作为研究对象）。蒸汽管道入口压强为P2，温度为T2；蒸汽管道出口压强为P3，温度为T3。用能装置作为一种供热设备，正常情况下的能源输入主要来源于三个方面：一是原材料；二是高温热蒸汽；三是由输电网络输送的电能。蒸汽通过生产设备释放热能，放热后凝结成液态水，然后通过回水管道再次进入锅炉，进行下一个循环。为用能设备所提供的电能一部分来自背压式汽轮机组，另一部分来自外接电源（分布式光伏、风电等）。

1.2 耦合能量网络中相关设备稳态模型

水和水蒸汽焓模型为

式 中，π=*；τ=T*；p*=16.53 MPa；T*=1 386 K；R=0.461 526kJ(kg·K)；ni、Ii、Ji为吉布斯自由能方程系数和指数值。

锅炉产蒸汽模型为

式中，h为水蒸气的焓；Hn和Cn分别为水蒸气在压力Pn、温度Tn下的焓值与比热容；q0为单位重量煤的发热量；vc为投运速度；η为锅炉的利用效率；Φ为单位时间焓值增加量。

背压式汽轮机模型为

式中，ΦCHP为汽轮机输出的热功率；PCHP为汽轮机输出的电功率；cm为热电比。

水和水蒸汽水力模型为

式中，d为管道直径；Ac为管截面面积；qm0、qm、qmi、qmq分别代表通过流入节点、管截面、流出节点、节点流向热负荷的质量流速；L为管流长度；ρ为流质密度；p0为管道出口处的压强；pi为管道入口处的压强；Ti为管道某端蒸汽温度；T0为管道首端蒸汽温度；Tω为环境温度；λ为管道导热系数；c为流体比热容。

用能装置模型为

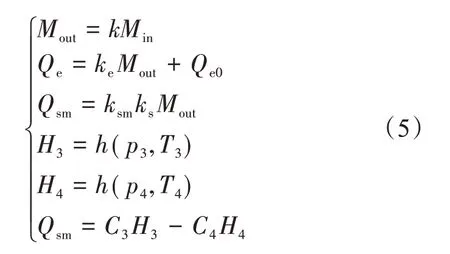
式中，mout为流出流量；min为流入流量；Tout为流出温度；Tin为流入温度；Qe为增加的发电量；Qe0为原始发电量；Qsm为转化之后的热量；ksm为电热转化系数；ks为热损失系数；ke电锅炉传热系数；k为总传热系数。

2 耦合能量网络方程

2.1 耦合能量网络方程的建模

根据广义基尔霍夫定律建立描述能量网络关系的方程组：

式中，A为关联矩阵；Bf为基本回路矩阵；H为广延量流量矩阵；ΔX为强度量差矩阵。

2.2 基于组合计算法的模型求解

本文所研究的系统在能源侧和能源负荷侧之间存在耦合关系，所以利用组合计算方法来解决这一问题，并按照分部的顺序对热网、耦合元件、电力系统这3 部分进行计算。在热网的潮流计算中，通过一系列模型计算流量，分别将管道流量带入不同模型进行计算，并对其进行迭代，从而得出热平衡节点的热功率。在耦合元件的计算过程中，只考虑热网对于电网在热电联供方面的影响。在电力系统的潮流计算中，用牛顿-拉斐逊法［8］计算电力系统，n个节点电力系统方程如下：

式中，Pi和Qi分别为节点i的有功功率和无功功率；为节点i的电压相量；为节点j的电压相量共轭值为节点导纳矩阵元素的共轭值。

3 算例分析

本文以阜新热电厂为例，建立含有热水传输模型、建筑物热负荷模型和背压式汽轮机组模型的耦合能量网络方程，并利用组合计算方法来求解，结果如图1～图6所示。

4 结论

1）从图1 看出，提高加热管道的保温隔热性能并适当提高管道内热水的输送速度，有利于提高加热效率。

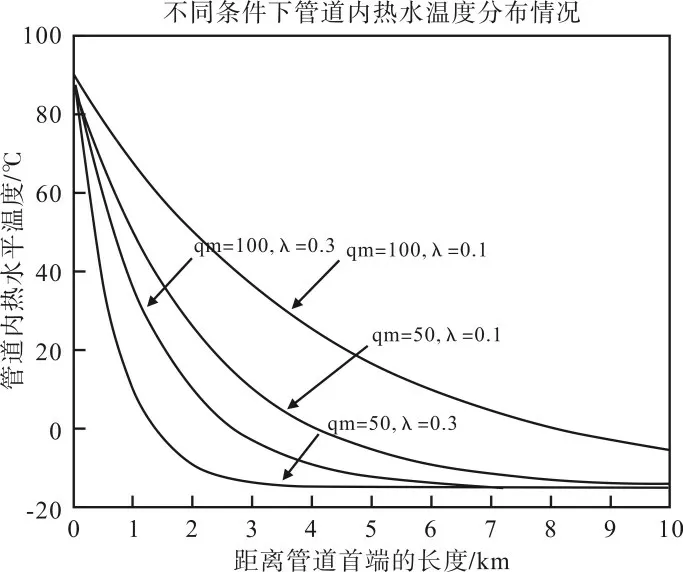
图1 不同条件下管道内热水温度分布情况

图2 暖气供水功率与燃煤供应速度的关系

图3 室内温度与热水流量的关系

图4 室内温度与电加热功率的关系

图5 减小热水流量室内温度变化

图6 降低供水温度后室内温度变化情况

2）从图2 和图3 看出，供暖热水功率与燃煤供应速度成线性关系，在能量利用效率不变的情况下，输入系统的能量等于输出系统的能量；此外，室内温度可以通过调节供热供水流量和供水温度来调节。

3）从图4、图5 和图6 看出，如果热水流量和温度突然变化，室内温度不会立即变化，而是会在一段时间内缓慢变化。利用这个缓慢变化的过程，可以临时调节供热功率，改变电/热分配和功率分配的比例。

上述结果与实际情况较为一致，由此证明本文所提出的计算方法和建立的模型是切实有效的，并为避免在生产实践中由于热力网络和电力网络的相互作用而导致生产过程大规模停产提供了理论支持。