疏勒河中游梯级水库库容和库水位关系模型优化

郑宗倩，张定海，王金辉，贾生海，白有帅，马 雁，寇 睿

(1.甘肃农业大学水利水电工程学院，甘肃 兰州 730070；2.甘肃农业大学理学院，甘肃 兰州 730070； 3.甘肃省疏勒河流域水资源局，甘肃 兰州 730070)

0 引言

随着社会经济的发展和人民生活水平的提高，我国水资源的供需矛盾显得越来越突出。人口激增和经济快速增长通常伴随着对供水和防洪机制的需求同样增长。因此，近年来，各种形式的水资源管理模式引起了人们的关注。水库在水资源分配系统中非常重要，如何使水库得到最优的运行决策，给水库的兴利调度提出了新的要求和标准。水库库容的准确测定是制定坝库优化调度策略必不可少的步骤。水库库容确定面临的主要挑战是水库库水位和库容之间关系的非线性行为。为了完成复杂水资源系统的规划和管理，需要优化操作程序[1]。确定水库库容与库水位之间的关系是其中一个非常重要的方面，不准确的库容量估算会导致水库蓄水库容的各种风险。

基于此，对于水库调度函数，国内外进行了广泛的研究，有学者通过回归分析来评估参数之间的关系(库容、高程和表面积)，但是发现从该分析中得到的模型不够精确[2]。归纳起来，基本上都是以各种优化模型得到的水库优化运行策略为基础，分析选择出决策变量和影响因子，把他们的关系表达成基函数的线性组合，进而确定出基函数的系数。这种方法不同程度上存在求解困难及结果难以精确表达因变量和自变量之间复杂关系的问题[3]。后续有学者通过人工神经网络(ANN)进行水库参数的研究分析，人工神经网络的强大非线性映射能力在求解这类问题时有着独特的优势[4]。胡铁松等[5]和高雅玉等[6]曾经用BP网络建立水库群单目标问题调度函数。针对疏勒河特殊的中游梯级水库，本研究以人工神经网络为主要的分析工具，给出了流域内3大梯级水库(昌马水库、双塔水库和赤金峡水库)库水位和库容之间的关系模型，以期获得更准确的结果，从而构成水库运行的基础，为水库运行管理和优化调度提供决策依据。研究方法也可用于预测其他水库库水位和库容之间的关系。

1 研究区概况

疏勒河灌区位于河西走廊西段的疏勒河中游地区，灌区内修有3座水库和3个子灌区[7]。3座水库分别是昌马水库、双塔水库和赤金峡水库，昌马水库和双塔水库位于疏勒河干流上，赤金峡水库位于相邻流域的石油河干流上，位置示意如图1所示[8]。3大水库的基本运行参数如表1所示。灌区总灌溉面积156.7 hm2(数据统计截至2017年，以下同)，3个子灌区灌溉面积分别为昌马灌区79.11 hm2，双塔灌区57.6 hm2，花海灌区20.03 hm2。

昌马水库与下游双塔水库形成串联梯级水库，联合水库能满足设计总灌溉面积7.08万hm2，工业需水8 275万m3；水电站装机容量1.425万kW，年发电量6 609万kW·h。双塔水库地处瓜州县城整栋48 km的乱山子处，水库始建于1958年，1960年建成蓄水，大坝所在区域的集水面积3.44万km2，水库前后已进行了4次加固[9]。水库上游有昌马堡和潘家庄两座水文站，该水库的水资源调度与昌马水库基本一致。赤金峡水库位于玉门市西北50 km处的石油河中游赤金峡，是一座以农业灌溉为主兼顾防洪的中型水库，始建于1958年，后经1962年、1966年2次加高扩建，最大坝高28.5 m，坝顶长220 m，总库容达到2 091万m3[10]。库存水源主要用于花海灌区用水，以及周边的生态和工农业用水。

2 研究方法

为了建立库水位和库容之间的关系模型，分别选取2003—2019年昌马水库、2009—2017年双塔水库和2008—2019年赤金峡水库的库水位和库容数据建立非线性回归模型。为了更好地对比神经网络模型的预测表现，将数据集分为训练集和测试集，分别将2003—2014年昌马水库、2009—2015年双塔水库和2008—2015年赤金峡水库的数据集作为神经网络的训练集，其他数据作为测试集[11-12]。同时，采用均方根误差(RMSE)、相对均方根误差(RRMSE)、平均绝对百分比误差(MAPE)以及效率系数(CE)来分析模型的表现情况。

2.1 回归分析

回归方法是描述两个或多个变量之间关系的经典方法，回归分析可以解释当任何一个自变量变化，而其他自变量保持不变时，因变量典型值的变化情况。

表1 疏勒河灌区3大水库的基本运行参数

通常，回归分析估计因变量的条件期望，即自变量保持不变时因变量的平均值。由于受到水库所在的地形、水库的流入和流出水量等因素的影响，水库的库水位和库容之间的关系常常呈现高度的非线性关系。利用Matlab软件采用高斯函数对3大水库的库水位和库容之间的非线性关系进行模拟，具体的模型如式(1)所示。

(1)

式中y——水库的库容

x——水库的库水位

a、b、c——模型的3个参数

2.2 前馈反向传播神经网络(FBNN)

前馈反向传播神经网络(feed forward back propagation neural network，FBNN)模型具有一个输入层、数个隐藏层(可以是一层，也可以是多层)和一个输出层，层与层之间采用全连接的方式，同一层神经元之间不存在相互连接，如图2所示。

理论上已经证明，具有一个隐藏层的3层网络可以逼近任意非线性函数。假定输入层包含I个节点，隐藏层包含J个节点，输出层包含K个节点，则输出zk可以表示为

(2)

式中f——传递函数或激活函数

xi——输入量

aij、bjk——加权值(i=1， 2， …I；j=1，2， …J；k=1， 2， …K)

aoj、bok——偏差

在式(2)中，函数f是一种将神经元从加权输入转换为输出的映射规则，也是一种将非线性影响引入FBNN网络的设计。FBNN传递函数的选择很多，在反向传播单元中，一般可以选择连续函数、可微、单调非减的函数作为传递函数。本研究选择二元logistic sigmoid函数作为传递函数，其定义如式(3)所示。

(3)

从FBNN模型结构可以看出，同一层内的每个单元之间并没有相互连接，相邻层之间的连接是基于加权系数来表示。同时，由于FBNN属于监督学习算法，其可通过调整网络中的加权值来获得最佳参数，最优是指网络输出zk和实际值或目标值tk达到最小值[13]。

(4)

为了让人工神经网络产生一个输出向量Y=(y1，y2， …yp)，尽可能接近目标向量Y=(t1，t2， …tp)，其训练过程也称为学习，被用来寻找最优的权重矩阵W和偏差向量V，使得给定的误差函数最小[14]。误差函数的形式如式(5)所示。

(5)

式中yi——期望输出T的分量

ti——相应的ANN输出

p——输出节点的数目

P——训练模式的数目

为了研究3大水库库水位和库容之间的关系，本研究中前馈神经网络的结果：输入层节点数为1个，表示各水库的库水位；隐藏层的节点数为10个；输出层的节点数为1个，表示各水库的库容。

2.3 径向基函数神经网络(RBF)

径向基函数(radial basis function，RBF)神经网络的结构与多层前向型网络相似，它是一种3层前向型网络，其网络结构如图3所示。在径向基函数神经网络中，将输入量输入到输入节点，再将其传递到隐含层，其上的每个神经元是由一个以多维度点为中心的径向基函数构成预测变量后，将各层接收到的加权输入相加[15]。径向基函数的结构由输入层、隐藏层和输出层组成。对于隐藏层，它的神经元个数是可变的(最佳神经元的数目由训练过程决定)。每个神经

元由一个径向基函数组成，其中心点的维数与预测变量的维数相同。

为了计算径向中心，在每个隐藏单元中使用高斯函数，它取决于输入到中心的距离，中心和扩散参数是需要确定的参数[16]。从高斯径向函数可以看出，隐藏单元对中心附近的数据点更敏感。最后，输出层将隐层神经元的值乘以与神经元相关联的权值，然后传递给输出层，求和将加权值相加，并将该和表示为网络的输出[17]。

采取监督学习的RBF神经网络模型，模型的参数由训练集给出，模型的评价由测试集给出，径向基函数的一般公式为

y(x)=Φ((x-c)TR-1(x-c))

(6)

式中Φ——模型中使用的激活函数

c——中心

R——距离的度量标准

((x-c)TR-1(x-c))是由R定义的输入x与中心c之间的距离。通常采用的是欧几里德距离，此时，R=r2，方程(6)可以简化为

(7)

欧几里德距离的长度用rj表示，rj用于测量基准矢量(神经网络的输出)y=(y1，y2， …ym)与径向中心Y(j)=(w1j，w2j， …，wmj)之间的径向距离[18]。yi和wij分别为网络的输入和权重，rj可以表示为

(8)

将适当的传递函数应用于rj得到

Φ(rj)=Φ(‖y-Y(k)‖)

(9)

输出层(k=1)结合Φ=(rij)的加权线性组合得到

(10)

模型的最终目标是通过使目标输出与实际输出之间的误差达到最小化来确定权重，通过训练RBF网络，调整权重因子，直到给定输入计算的输出模式与期望输出相匹配。

2.4 模型评价标准

利用非线性回归、RBF和FBNN网络来预测昌马水库、双塔水库、赤金峡水库库水位与库容之间的关系。为了评估模型的性能，使用均方根误差(RMSE)、相对均方根误差(RRMSE)和平均绝对百分比误差(MAPE)评估每个模型的预测结果。RMSE，RRMSE和MAPE的计算公式分别如下

(11)

(12)

(13)

通常，RMSE和RRMSE是基于对实际模型和预测模型之间的估计误差的比较来评估模型，误差最小的模型被认为是最佳选择。有研究指出，MAPE约30%时被认为是合理的预测[19]。当MPAE在5%～10%时，结果被认为是非常准确的。利用效率系数(CE)来衡量模型准确的效率，CE的值由式(14)给出。CE值越大(最大值为1)表明该模型的预测性能越是有效的。

(14)

式中Da(t)——实际值

Df(t)——预测值

n——预测期数

3 结果与分析

使用Matlab软件采用非线性回归方法、FBNN神经网络和RBF神经网络对3大水库库水位和库容之间的关系进行模拟，具体结果如下。

3.1 非线性回归模型

研究选取高斯函数作为3大水库库水位和库容之间关系的非线性回归模型，利用选取3大水库库水位和库容的数据进行回归分析，回归系数分析结果如表2和图4所示。

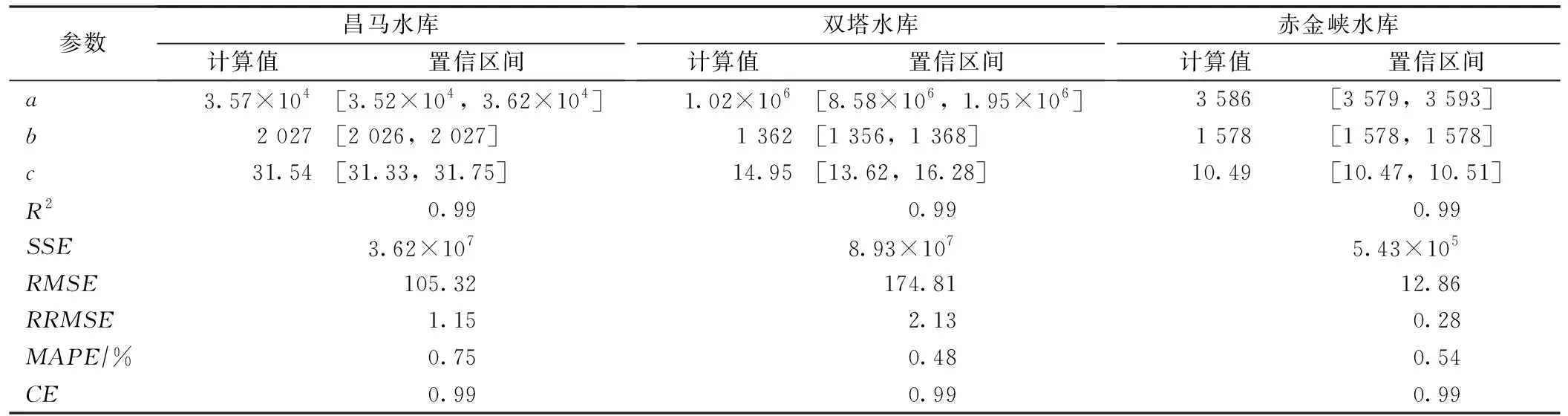
表2 水库库水位和库容之间的非线性回归分析计算结果

由表2和图4可以看出，当显著性水平α=0.05时，3大水库库水位和库容之间的相关系数R2均>0.99，3个模型的显著性概率R<0.05，这说明高斯函数模型可以较好地拟合库水位和库容之间的关系。

3.2 神经网络模型

3大水库库水位和库容之间的神经网络性能指标和神经网络拟合结果如表3和图5～6所示。由表3可以看出，FBNN和RBF神经网络均可较好地拟合3大水库的库水位和库容之间的关系。但相对而言，RBF神经网络对昌马水库和双塔水库的库水位和库容模拟较好，FBNN神经网络对赤金峡水库的库水位和库容模拟较好。对昌马水库和双塔水库而言，基于RBF神经网络较FBNN神经网络的均方根误差(RMSE)、相对均方根误差(RRMSE)及平均绝对百分比误差(MAPE)均有所降低。对赤金峡水库而言，基于FBNN神经网络比RBF神经网络的均方根误差(RMSE)、相对均方根误差(RRMSE)及平均绝对百分比误差(MAPE)均有所降低。

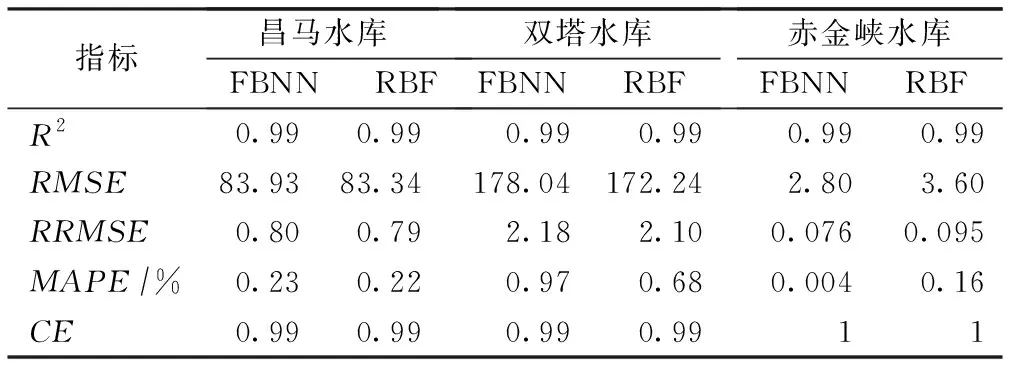
表3 水库库水位和库容之间的神经网络性能指标

4 结论

人工神经网络(ANN)模型具有良好的水文过程模拟能力，与其他传统模型相比，它是处理复杂问题的有效且实用的工具。水库坝库优化调度决策影响因素多，关系复杂，在供蓄水期末更是如此，这时采用线性模型结果波动大，稳定性差，而ANN模型强大的非线性映射能力刚好可以满足这方面的要求。人工神经网络能够给出比其他方法更为准确和敏感的结果，特别是在建立水库库容与库水位之间关系模型时。利用Matlab软件建立库水位和库容之间的非线性关系模型，并建立了以库水位为输入，库容水位为输出的两种神经网络。结果表明：高斯函数可以很好地拟合3大水库的库水位和库容之间的关系，制定更精确的水库库容与库水位关系模型。同时，对于昌马水库和双塔水库而言，RBF神经网络的拟合较FBNN神经网络好；对于赤金峡水库，FBNN神经网络较RBF神经网络的拟合好。模拟结果可以作为疏勒河中游梯级水库优化及运行调度的重要参考依据。