基于学习自动机的容噪模式分类

摘要：在模式分类学习问题中，训练数据中的标注差错（也称类别噪声）对分类器的性能有很大的影响。本文将一种新近提出的连续动作学习自动机（即聚焦区间学习自动机）应用于针对类别噪声的容噪学习问题。分类器采用简单的单隐层前馈神经网络，利用一个由这种学习自动机组成的自动机团队，对神经网络的权值参数进行学习。通过广义异或问题和Iris数据集的仿真试验，将该算法与两种基于群体搜索的优化算法——粒子群优化（PSO）和差分进化（DE）进行了比较研究。结果表明，新算法具有更好的容噪学习性能。

关键词：模式分类；类别噪声；容噪学习；学习自动机；连续动作学习自动机

中图分类号：TP181文献标识码：ADOI：10.19452/j.issn1007-5453.2020.10.012

模式分类是机器学习领域中的一个重要课题，相关研究非常活跃。以航空领域为例，无人机的目标检测、飞机部件的故障诊断等都属于模式分类问题[1-2]。分类器的构造可以视为一种学习过程，即通过对一个经标注的数据集（训练集）的学习，建立从特征空间到类别空间的映射关系。显然，训练数据的质量对最终的学习结果会有影响。在传统的学习理论中，用于训练的数据是不含噪声的。但实际应用中的训练数据未必都这样理想，当其中含有噪声时，训练出的分类器的性能有可能大打折扣。训练数据中的噪声可分为属性噪声和类别噪声两大类[3-5]。属性噪声也称特征噪声，是指训练样本中的特征参数受到了噪声的干扰。类别噪声也称标注噪声，是指一个样本被赋予了不正确的类别标签。

研究表明[3-5]，相对于特征噪声，类别噪声通常具有更大的潜在危害。許多著名的分类方法（如支持向量机及AdaBoost等）对类别噪声都很敏感。由于获取可靠的标注数据昂贵而费时，故标注工作不一定总由领域专家来完成，尤其在互联网和大数据背景下，经常是由非专业人员甚至计算机自动完成的。这就有可能引入标注噪声。在某些场合，如疾病或设备故障的诊断等，因问题的复杂性，即使专家标注的数据也不能保证100%的准确。因此，研究针对类别噪声的容噪学习技术，具有十分重要的意义。

应对类别噪声的最常用的一种方法是先通过某种技术，识别并过滤掉训练数据中被错误标注的数据样本，再用正确无误的数据集进行学习。参考文献[6]提出一种基于距离的检测方法，以发现异常数据样本。参考文献[7]采用模型过滤法，剔除错标的数据。参考文献[8]利用交叉验证的方法，对数据中的孤立点进行鉴别和筛选。对付类别噪声的另一种方法，是采用具有容噪能力的学习算法。参考文献[9]针对多核学习问题，提出一种基于复合梯度映射的学习算法，但其中有一个假设，即标注差错的概率是已知的。这会限制其实用性，因为在实际中该概率很难预先知道。参考文献[10]提出一种基于混合模型的稳健判别方法，其中也有个假设，即样本总体是正态分布的。参考文献[11]和参考文献[12]在不对训练样本做特别假设的情况下，将一类连续动作学习自动机应用于类别噪声下的容噪学习，取得了很好的结果，不过其学习对象仅限于线性的二分类问题。

本文尝试将一种较新的连续动作学习自动机，即基于窗口-奖励的聚焦区间学习自动机[13-15]，应用于非线性多分类问题的容噪学习。

1学习自动机

学习自动机（learning automata，LA）是一类自适应决策算法。自动机通过与一个随机环境的不断交互，学习最佳的输出动作[16]。在任一时刻，LA根据某种概率分布，从其动作集里选择一个动作并输出给环境；环境则反馈一个强化信号，作为对LA所选动作的评价。根据该评价，LA更新其概率分布，以期下次能选出更合适的动作。作为一种随机优化方法，LA很适合处理具有非线性及不确定性的优化问题。

根据动作集的性质，LA可以分为有限动作学习自动机（finite-action learning automata，FALA）和连续动作学习自动机（continuous-action learning automata， CALA）两大类。FALA适合处理组合优化问题，CALA则适合处理连续型的数值优化问题，如神经网络权值的训练。

2 FILA/WR

现有的几种CALA都是采用高斯分布作为其动作选择的概率模型，自动机通过不断调整高斯分布的均值和标准差实现学习[16]。与此不同，本文作者提出一种新的CALA[13-15]，其利用一个可变区间作为动作集，并按照均匀分布方式产生输出动作。学习算法根据一个滑动窗口内的最佳的历史动作，对区间的两个端点进行更新。由于该自动机对动作区间的更新类似于一种调焦或对焦，故称之为聚焦区间学习自动机（focused interval learning automaton， FILA）。

记动作区间为[xL，xR]。为对其进行更新，算法保持一个滑动窗口W={（x（i）， J（i））|i=k-M+1，…， k}，其中（x（i）， J（i））为最近的自动机与环境交互的历史记录（输出的动作参数及相应的目标函数值），x（i）代表在i时刻自动机选出的动作参数，J（i）是x（i）的目标函数J（x（i））的简写。为高效实现，W采用环形队列的方式存储最近的M对x和J。M为窗口大小。

在任一时刻k，自动机以均匀分布方式在当前的区间上随机选择一个实数x（k），称为动作，并从环境得到对应的目标函数J（k）。将x（k）和J（k）放入W中。然后，找出其中具有最小J（x）值的动作（针对最小化问题），将其记为xb。再根据xb对区间的两个端点进行更新。

因该算法总关注一个滑动窗口，并将动作区间朝窗口内最佳的动作xb的方向调整，相当于对xb进行奖励，故可进一步将其记做FILA/WR，其中W与R分别代表窗口（window）和奖励（reward）。我们曾将该算法应用于不同的问题，如被噪声污染的多模态函数的全局优化[13]、非线性系统辨识与建模[14]以及动态不确定性环境下的在线学习[15]。在这些应用中，FILA/WR在学习精度、运行结果的一致性尤其是最差情况下的性能表现，都有明显的优势。

3仿真试验

本文尝试将上述FILA/WR应用于针对类别噪声的容噪模式分类问题。分类器采用单隐层前馈神经网络，利用该算法对网络的权值参数进行学习。训练前馈神经网络的经典方法是误差反传（BP）算法。这是一种梯度下降方法，很容易陷入局部最优。近些年来，以遗传算法（GA）、粒子群优化（PSO）以及差分进化（DE）为代表的基于群体计算的智能优化算法，被广泛应用于神经网络的训练。为检验FILA/WR的学习性能，本文选择目前流行的PSO[17]和DE[18]进行对比试验。DE有多个版本，本文采用的是DE/rand/1/ bin版本，其在工程优化问题中应用最为广泛。

我们选取了两个测试问题，一个是广义异或问题，一个是鸢尾花数据集。前者属于二分类问题，后者则属于多分类问题。对每个问题，分别在训练样本中人为地引入不同强度的类别噪声，以测试学习算法的容噪性能。

3.1广义异或问题的试验

广义异或问题是一个2特征、2类别的人造分类问题。设模式空间为x-y平面内的矩形区域[-1，1]×[-1，1]。该区域内的任一点p（x，y）属于两个類别之一：位于第一、第三象限内的点为A类，位于第二、第四象限内的点为B类。即A类点的x、y坐标同号，B类点的x、y坐标异号。这是一个典型的非线性可分问题，其可以看作是二值的异或（XOR）问题在连续域的推广。参考文献[19]曾利用基于PSO和BP混合训练的神经网络来解决该问题，但其训练数据不含噪声，且网络结构比较复杂，为双隐层。

本文采用一个单隐层的前馈神经网络，网络结构为2-8-1。其中有两个输入节点，分别对应待分类模式的x和y坐标；一个输出节点，代表类别标签：1表示A类，-1表示B类；一个隐藏层，包含8个节点。整个网络一共有33个需要确定的权值参数（包括阈值）。所有节点的激活函数均采用双曲正切函数。由于一个自动机只处理一个参数，故使用33个FILA，每个自动机负责一个参数。33个自动机构成一个LA团队[14]，以合作博弈的方式学习网络的最佳权值。

在区域[-1，1]×[-1，1]中随机抽取2000个点作为训练样本，再在同一区域以x、y坐标均按0.02的间隔均匀抽取10000个点作为测试样本。为检验学习算法的容噪性能，对训练样本中的类别标记进行人为翻转（即A变B、B变A），以引入类别噪声。其中噪声强度（错误标签在训练样本中所占的比例）分别取0（即无噪声），10%，20%，30%和40%。训练采用批次方式，即对于PSO、DE或FILA团队产生的每一组权值参数，计算所有训练样本下网络输出节点的均方误差，以此作为该组权值参数的目标函数。一次仿真，总共评估10000个目标函数值。

FILA的内部参数设置如下：M=20，λ=0.005，δ=0.01。对于PSO和DE，先分别进行若干次试探性试验，然后取效果较好的参数组合，具体情况如下：PSO中粒子群的规模为50，惯性权重w为0.5，加速度常数（学习因子）c1和c2均为1.5，每一维的最大速度取vmax_ratio*di，其中di为相应维初始搜索区间的长度，vmax_ratio为0.2。对于DE，群体规模NP取25，缩放因子F取0.3，交叉概率CR取0.8。对每种算法，33个待优化权值的初始搜索区间均取[-2，2]。

训练结束后，PSO和DE取群体中的最优解（即目标函数最小的权值参数），FILA则取最终每个动作区间的中点所构成的权值参数。再利用权值参数分别为这三组值的神经网络对测试集进行分类，当输出节点的激活值大于0时判定为1（即A类），否则判定为-1（即B类）。

为获得可靠的结论，在每一种噪声水平下，分别用三种算法各做100次独立试验（每次训练集及标注噪声都重新产生，但各算法相同），统计训练好的神经网络在测试集上的分类结果。表1给出了不同噪声水平下三种算法得到的识别率的平均值及标准差。

由表1可以看出，在不含噪声的情况下，三种算法均获得了98%左右的平均识别率（FILA最好，DE最差）。参考文献[19]中，5次试验的平均识别率为99.55%，但其所用的神经网络为较复杂的双隐层结构，且采用PSO和BP结合的训练方法；该文也没有研究训练样本含有噪声的情况。

由表1可知，当训练数据含有标注噪声时，三种算法训练出的神经网络的性能会有所下降，但下降幅度比样本差错的比率要小得多。即使在40%的噪声水平下（训练样本的标注正确率只有60%），DE也有超过86%，PSO和FILA则有超过88%的平均识别率。这说明，神经网络本身就具有较好的噪声容忍能力，其“记住”的是训练集的整体特征。由表1还可看出，5种情况下，FILA的平均识别率有三次高于PSO，两次低于PSO，而标准差则有4次小于PSO，仅有一次大于PSO，这表明其性能更稳定，结果的一致性更好。相比之下，DE的效果最差，其不仅平均分类正确率低，标准差也比较大。

其实，我们还曾利用经典的误差反传（BP）算法训练上述网络，但其效果极不稳定。仅就不含噪声的情况而言，BP有时很快就找到了识别率高达100%的网络权值，但有时却仅得到50%的识别率（此时神经网络对输入样本的反应完全是随机的）。仔细分析发现，这是由于训练陷入了误差曲面的平坦区域，因梯度过小（<10-10）而导致训练提前中止，网络权值没有收敛。鉴于此，后文将不再考虑BP，仅对FILA、PSO和DE进行仿真。

3.2 Iris數据集的试验

鸢尾花（Iris）分类是模式识别和数据挖掘领域中一个被广泛引用的经典问题。有三种鸢尾属植物，分别称作iris-setosa，iris-versicolor和iris-virginica。每一品种各采集了50个样本，每个样本包含4个特征参数：萼片的长度和宽度、花瓣的长度和宽度。我们的任务是构造一个分类器，用以识别任一给定的数据样本属于三个品种中的哪一个。这是一个4特征、3类别的分类问题，其中iris-setosa与另两个类别是线性可分的，后两者则不是线性可分的。参考文献[19]～[21]曾用不同的方法对该问题做过试验研究，其中参考文献[21]还考虑了训练数据中含有属性噪声的问题，但都没有考虑类别噪声。参考文献[11]和参考文献[12]采用一种基于高斯分布的CALA来解决类别噪声下Iris数据集的容噪学习问题，但其工作仅限于线性的二分类问题（将iris-setosa作为一类，另外两类则合并为一个大类）。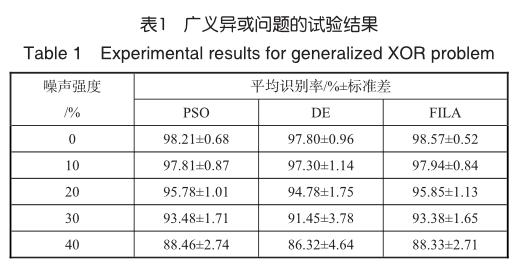

本文采用一个4-5-3结构的神经网络，解决上述Iris数据集的三分类问题，分别利用PSO、DE和FILA来学习网络的43个权值参数。试验所用的数据来自UCI数据集。因该数据集的特征参数未归一化，故网络权值的初始搜索区间取得小一些，为[-0.5，0.5]。训练时，从150个数据样本中随机抽取90个（每一品种各30个）作为训练集。训练结束后，用所有数据样本（包括训练样本，但不加噪声）进行测试。测试时，网络的三个输出采用“高胜”逻辑。

试验发现，前面针对广义异或问题设置的DE的那一组参数，对Iris数据集的学习效果相当差。为此，我们重新试探了其参数组合，最终选用的是：NP=20，F=0.4，CR=0.8。PSO和FILA的内部参数仍沿用前一试验的设置。试验结果见表2。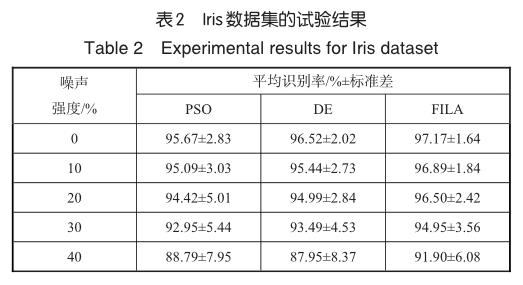

由表2可以看出，在训练数据不含噪声的情况下，三种算法的平均分类正确率均在96%左右（FILA略高于97%）。参考文献[20]采用交叉验证K近邻算法，得到的识别率为96.67%。参考文献[19]的5次试验的平均识别率为98.53%，但其网络有两个隐藏层，结构较复杂，且其训练方法同时使用了PSO和BP。这些文献均未考虑训练数据含有噪声的问题。

再看训练数据包含类别噪声的情况。由表2可以看出，对于Iris数据集，FILA在每种噪声水平下的平均识别率都比PSO和DE的高。在训练数据含有40%的标注噪声的情况下，FILA仍可获得接近92%的分类精度（PSO和DE则不到89%）。另外，与PSO和DE相比，FILA的标准差更小，这说明其鲁棒性更好。与第一个试验不同的是，对Iris数据集，除噪声水平为40%的情况外，PSO的结果总差于DE。这说明，在这两种算法中，没有哪个更具优势。

前面说过，在Iris数据集的试验中，对DE的内部参数进行了重新设置。如果沿用第一个试验中的参数，则学习结果明显差于表2中的数据。反过来，上述的对于Iris数据集效果较好的这组参数，当应用于广义异或问题时，效果也远差于表1中的结果。这说明DE对于要解决的问题较为敏感，不同的问题需要不同的算法参数。

4结束语

训练样本中的标注噪声对分类器的学习构成很大的挑战。本文研究了神经网络分类器的容噪学习问题，其中的训练数据允许存在类别噪声。我们将一种新近提出的FILA/WR算法应用于神经网络权值的学习。该方法既不需要对训练数据进行预处理，也无须样本噪声的任何先验知识。

通过广义异或问题和Iris数据集，对该算法和两种流行的群体优化算法——PSO和DE算法进行了试验比较。结果表明，在各种噪声水平下，由新算法训练出的神经网络具有更好的分类性能。该算法容噪能力强，结果稳定性好。另外，与DE相比，新算法的内部参数对于待求解的问题不敏感，因而更易于使用。下一步，我们拟将该算法应用于航空领域中的一些机器学习问题，如基于神经网络的发动机故障诊断和寿命预测等。

参考文献

[1]王晓华，张聪，李聪，等.基于仿生视觉注意机制的无人机目标检测[J].航空科学技术， 2015， 26（11）： 78-82. Wang Xiaohua， Zhang Cong， Li Cong， et al. Unmanned aerial vehicles target detection based on bio-inspired visual attention[J]. Aeronautical Science & Technology， 2015， 26（11）： 78-82.（in Chinese）

[2]熊天旸，张先辉，李新民，等.基于BP神经网络的自动倾斜器轴承故障诊断[J].航空科学技术， 2017， 28（11）： 69-73. Xiong Tianyang， Zhang Xianhui， Li Xinmin， et al. Fault diagnosis method of swash-plate bearing based on BP neural networks[J]. Aeronautical Science & Technology， 2017， 28（11）： 69-73. （in Chinese）

[3]Zhu Xingquan，Wu Xindong. Class noise vs. attribute noise：a quantitative study[J]. Artificial Intelligence Review，2004，22（3）：177-210.

[4]Fréncy B，Verleysen M. Classification in the presence of label noise：a survey[J]. IEEE Transactions on Neural Networks and Learning Systems，2014，25（5）：845-869.

[5]宮辰，张闯，王启舟.标签噪声鲁棒学习算法研究综述[J].航空兵器， 2020， 27（3）： 20-26. Gong Chen， Zhang Chuang， Wang Qizhou. A survey of label noise robust learning algorithms[J]. Aero Weaponry， 2020， 27（3）： 20-26. （in Chinese）

[6]Knorr E M，Ng R T，Tucakov V. Distance-based outliers：algorithms and applications[J]. VLDB Journal，2000，8（3）：237-253.

[7]Brodley C E，Friedl M A. Identifying mislabeled training data[J]. Journal of Artificial Intelligence Research，2011，11（1）：131-167.

[8]张健沛，杨显飞，杨静.交叉验证容噪分类算法有效性分析及其在数据流上的应用[J].电子学报， 2011， 39（2）： 378-382. Zhang Jianpei， Yang Xianfei， Yang Jing. Effectiveness analysis and application in data streams of cross validation noisetolerance classification algorithm[J]. Acta Electronica Sinica， 2011， 39（2）： 378-382. （in Chinese）

[9]龙文光，刘益和.多核学习中基于复合梯度映射的学习算法研究[J].计算机应用研究， 2015， 32（4）： 1019-1023. Long Wenguang， Liu Yihe. Research on learning algorithm based on composite gradient mapping in multiple kernel learning[J]. Application Research of Computers， 2015， 32（4）： 1019-1023. （in Chinese）

[10]朱德刚.一个稳健判别方法及应用[J].数学的实践与认识， 2019， 49（6）： 161-165. Zhu Degang. A robust discriminant approach and its application[J]. Mathematics in Practice and Theory， 2019， 49（6）： 161-165.（in Chinese）

[11]Sastry P S，Nagendra G D，Manwani N. A team of continuousaction learning automata for noise-tolerant learning of halfspaces[J].IEEETransactionsonSystems，Man，and Cybernetics，Part B，2010，40（1）：19-28.

[12]Manwani N，Sastry P S. Noise tolerance under risk minimization[J]. IEEE Transactions on Cybernetics，2013，43（3）：1146-1151.

[13]刘晓.一种鲁棒的连续动作学习自动机[C]//全国抗恶劣环境计算机第二十五届学术年会， 2015： 266-271. Liu Xiao. A robust continuous-action learning automaton [C]// CCF TCSEC. Proceedings of 25th Severe Environment Computer Conference， 2015： 266-271. （in Chinese）

[14]刘晓.基于智能计算的非线性系统辨识与建模[C]//全国抗恶劣环境计算机第二十五届学术年会， 2015： 251-255. Liu Xiao. Nonlinear system identification and modeling based on intelligent computation[C]//CCF TCSEC. Proceedings of 25th Severe Environment Computer Conference， 2015： 251-255. （in Chinese）

[15]刘晓.一种求解动态及不确定性优化问题的新方法[J].微电子学与计算机， 2016， 33（7）： 83-88. Liu Xiao. A new method for solving dynamic and uncertain optimization problems[J]. Microelectronics & Computer， 2016， 33（7）： 83-88. （in Chinese）

[16]Thathachar M A L，Sastry P S. Varieties of learning automata：an overview[J]. IEEE Transactions on Systems，Man，and Cybernetics，Part B，2002，32（6）：711-722.

[17]Kennedy J，Eberhart R C. Particle swarm optimization[C]// Proceedings of IEEE Internal Conference on Neural Networks. Piscataway：IEEE，1995.

[18]Das S，Suganthan P N. Differential evolution：a survey of the state-of-the-art[J]. IEEE Transactions on Evolutionary Computation，2011，15（1）：27-54.

[19]田雨波，潘朋朋.混合粒子群算法優化神经网络的研究[J].微电子学与计算机， 2011， 28（6）： 156-159. Tian Yubo， Pan Pengpeng. The research of neural network based on hybrid particle swarm optimization[J]. Microelectronics& Computer， 2011， 28（6）： 156-159. （in Chinese）

[20]汪庆华，刘江炜，张兰兰.交叉验证K近邻算法分类研究[J].西安工业大学学报， 2015， 35（2）： 119-124. Wang Qinghua， Liu Jiangwei， Zhang Lanlan. Study on the classification of K-nearest neighbor algorithm[J]. Journal of Xian Technological University， 2015， 35（2）： 119-124. （in Chinese）

[21]蒋雯，陈运东，汤潮，等.基于样本差异度的基本概率指派生成方法[J].控制与决策， 2015， 30（1）： 71-75. Jiang Wen， Chen Yundong， Tang Chao， et al. Determination of basic probability assignment based on sample difference degree[J]. Control and Decision， 2015， 30（1）： 71-75. （in Chinese）

（责任编辑王为）

作者简介

刘晓（1965-）男，高级工程师。主要研究方向：动力控制和智能计算。

Tel：029-89186505

E-mail：xiao.liu@163.com

Noise-Tolerant Pattern Classification Based on Learning Automata

Liu Xiao*

AVIC Xian Aeronautics Computing Technique Research Institute，Xian 710065，China

Abstract： In the learning problem of pattern classification， the label error （also called class noise） in the training data can severely impact the performance of the classifiers. A recently proposed continuous-action learning automaton， i.e.， the focused interval learning automaton is applied to the noise-tolerant learning for the class noise. The classifiers adopt simple single hidden-layer feed-forward neural networks. A team of such learning automata is used to learn the weight parameters of the network. Simulations are carried out which employ the new algorithm and two populationbased optimization algorithms， particle swarm optimization （PSO） and differential evolution （DE）， respectively， on the generalized XOR problem and the Iris dataset. The simulation results indicate that the new algorithm can obtain better noise-tolerant learning performance compared with the PSO and DE.

Key Words： pattern classification； class noise； noise-tolerant learning； learning automata； continuous-action learning automata