回归模型在传染病传播范围上的研究及应用

戴彩艳 李新霞 丁有伟 何菊 胡孔法

（南京中医药大学人工智能与信息技术学院 江苏省南京市 210000）

1 背景

近年来，随着气候的变化，出现了不同种类的传染病，有一些甚至在短短的时间内，传播了很大范围[1]。这使得很多国家和地区出现医疗需求和供给极度不平衡，医护人员及资料物资短缺，在病患者人数达到一定数目的时候，采用了不得不用的措施去应对。造成了很多原本可以获救的人失去了生命。

传染病，与海啸、地震等灾难出现后[2,3]再进行灾后快速调度人员、物资进行救援的情况有所不同。原因是一些传染病传染速度之快，如果没有对传染病的传播情况及致死率重视起来，那么情况将朝着不可控的发向发展。因此对传播人数进行提前预测，可以提前对有可能发生大规模传染病的地区进行预警，以便提前配备医护人员和医疗物资，减少不必要的人员伤亡现象。

数据挖掘中的预测技术就是根据之前出现的一系列情况进行模型训练，在此技术上对未来有可能发生的情况进行估计[4,5]。因此本文某地区1月份到8月份的传染病人数变化情况的基础上进行传染病传播人数预测。以为类型相近的传染病提供传播人数的预测，为政府和人民提供传染病传播的理论依据，便于提前布控。

2 相关工作

模型训练中使用的一元线性回归模型[6,7]和自回归移动平均模型(ARMA)[8,9]都属于有监督学习，分别对其描述如下：

2.1 一元线性回归模型

回归分析被用来对两个或者多个变量之间存在的联系通过方程进行模拟。会将一些已经出现的数据作为模型训练的输入，对应还有其输出；可以抽取原数据集中的部分数据（未参与训练的数据）对模型的准确性进行检验。当输入的数据为一个时，就称作一元线性回归；而输入的数据超过一个时，则称作多元线性回归。

其中一元线性回归的方程表示如下：

当参数训练好之后，这个方程就会对应一条直线，这条直线被称为回归线。

其中θ0为该回归线的斜率，b 对应该回归线的截距。

2.1 自回归移动平均模型

自回归移动平均模型(ARMA,auto regression moving average model)结合了AR 模型(auto regression model)、MA 模型(moving average model)，通常在拟合平稳时间序列时使用。

通常包含两个参数，分别是自回归阶数p 以及平均移动阶数q。其对应的方程如下：

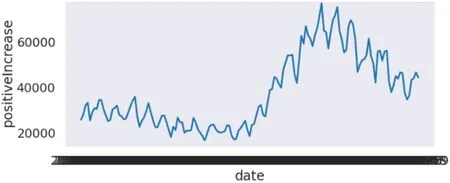
图2：4月1日之后新增传染人数走势图

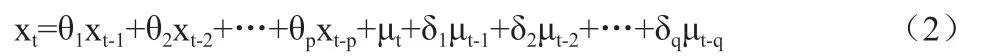
其中，θ1,θ2,…,θp对应的是自回归系数，而μ1,μ2,…,μp对应的是移动平均系数，都是模型的待估参数。

一元线性回归和自回归移动平均模型都属于回归模型，在具体应用中预测性能有所不同。

3 算法使用框架

对训练数据集所采用的两种不同模型的使用过程描述如下：

3.1 一元线性回归使用过程

使用一元线性回归的过程描述如下：

（1）确定训练集和测试集的输入及输出；

（2）根据训练集进行模型的训练，训练过程中，使用到的代价函数如下：

其中y 和fθ(x)分别对应的是输出的真实值和预测值。

使用最小二乘法求出取得最小的代价函数时，对应的参数。

（3）将测试集带入训练出的模型，比较真实值和预测值之间的差异，以衡量模型的性能。

表1：使用一元线性回归对应的部分真实数据与预测数据的误差及误差比例

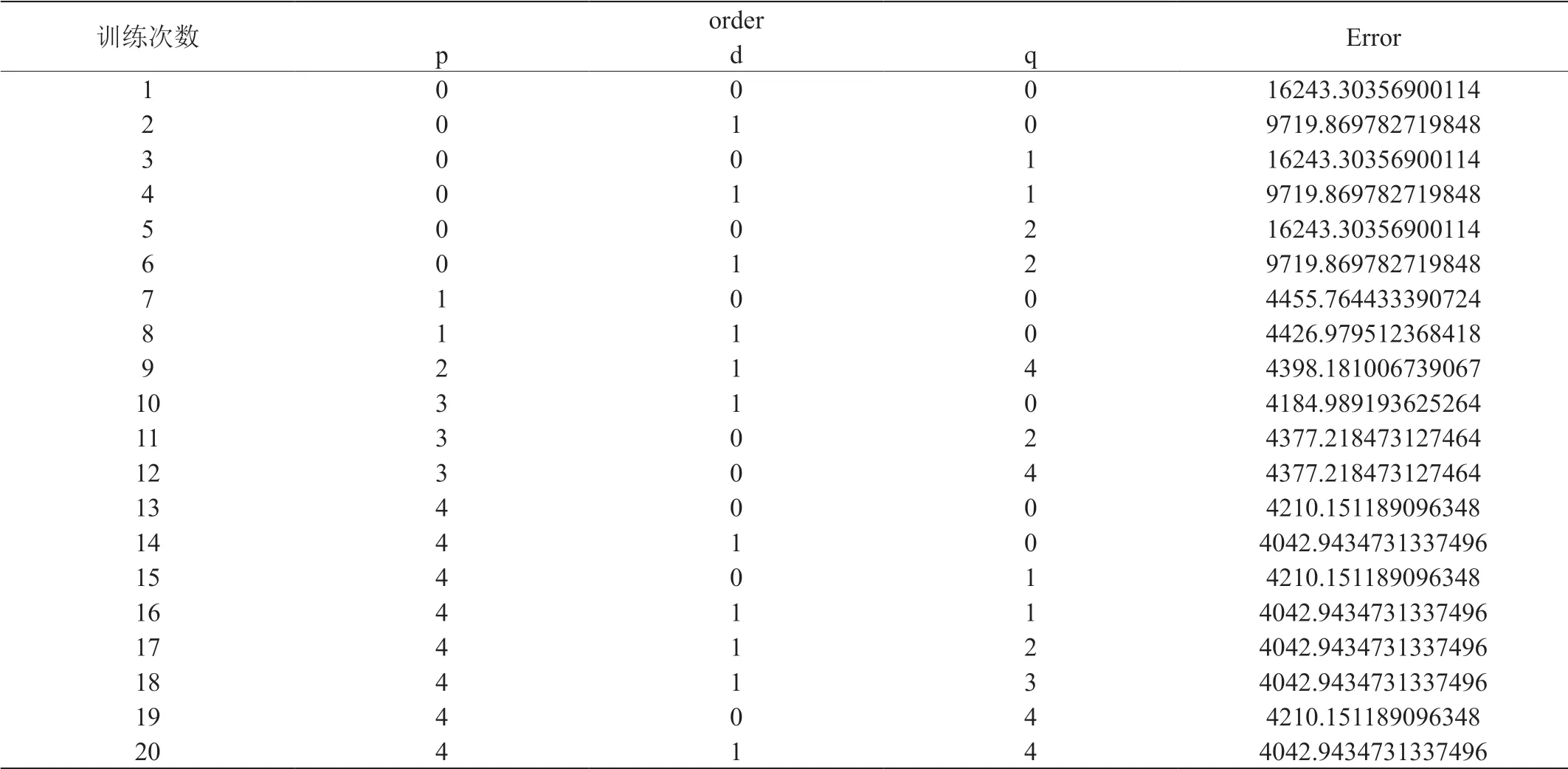
表2：Error 值随着参数变化的情况表

表3：测试集中的部分真实数据与预测数据的误差及误差比例

3.2 自回归移动平均模型使用过程

使用自回归移动平均模型的过程描述如下：

3.2.1 数据选取

用观测、调查、统计、抽样等方法取得被观测系统时间序列动态数据

3.2.2 参数训练

对其中涉及到的参数进行训练，选择最优参数。

3.2.3 测试及性能比较

根据训练的模型，输入测试集进行测试，并对模型的性能进行评价。

可以按照上述过程对数据集中选取出的有效数据进行模型训练。训练过程中关键的是模型参数的选取。

4 实验

4.1 实验环境

实验采用的是某地区公开的传染病传播人数的数据，可以从https://pan.baidu.com/s/129j6iY6s5lKyeWJjBvKLJw 下载到。包含的数据时间节点是从2020年1月22日到2020年8月29日。在Window10 环境下，采用python 3.7 编程实现。

4.2 数据选取

首先查看数据集中新增传染人数的变化趋势，读取到的数据集可图示如图1 和图2所示。

从图中可以看出最开始的一个多月时间内，新增传染人数还未增加很多，原因在于政府未重视或传染病传播情况不明显等，数据在预测传播人数时所起作用不大，因此提取4月1日之后的数据作为研究对象。

将最后的5 天数据作为测试数据，其他的作为训练数据。分别使用一元线性回归和ARMA 模型进行预测这5 天该传染病传播的人数。

4.3 使用一元线性回归进行预测

训练集中的数据x 选取的是数据集中对应的真实日期，而y 选取的是数据集中的positiveIncrease 列(即增加的检查结果为阳性的人数)。可以得到如表1 预测结果。

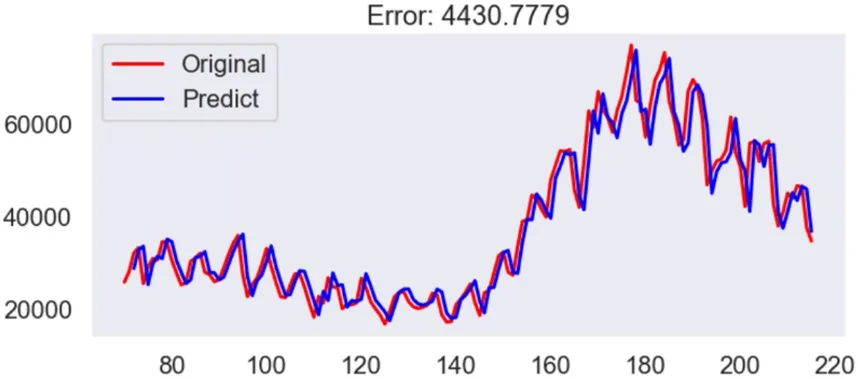
图3：预测值和真实值之间的误差

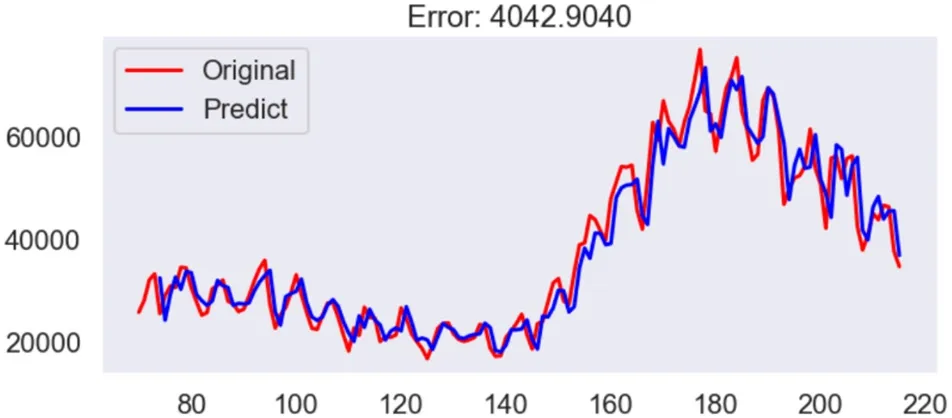
图4：真实值与预测值的比较情况图

4.4 使用自回归移动平均模型（ARMA）进行预测

4.4.1 指定一组参数进行训练

定义模型为ARMA 并开始训练，设置参数order=(2,0,0)，该参数与模型的识别问题和定阶问题有关，包括的三个参数分别对应p，q，d 三个参数，其中p 为自回归阶数，平均移动阶数为q，而d 为差分的阶数。接下来使用训练好的模型预测并计算预测值和真实值之间的误差。该误差计算公式如下：

显示结果如图3所示。

4.4.2 遍历多组参数，寻找最优参数

设置order=(p,d,q)，其中p、q 的取值范围在5 以内，d 的取值范围在2 以内。随着参数的变化，error 的值也不断发生着改变。部分变化趋势情况如表2所示。

通过error 值随着参数变化的情况，最终选取order=(4,1,0)。在此基础上，进行将测试集带入模型开始进一步训练。

4.4.3 预测并测试结果

当选取好最优参数之后，即对应的error=4042.9434731337496 ≈4042.9435。在这个前提下，得到的真实值与预测值的比较情况如图4所示。

具体测试集中的部分真实数据与预测数据的误差及误差比例如表3所示。

通过上述实验可以发现，自回归移动平均模型比一元线性回归模型在该传染病传播人数预测中的准确率要高。在预测过程中，其中2020年8月25日误差最小，只有1.1354%。原因在于，自回归移动平均模型中各影响因素在较短的时间内，预测指标的相对变化规律是近乎相同的，所以基于这样的预测指标，对同样的数据进行预测可以在很大程度上确保预测结果的准确性。而且自回归移动平均预测模型不直接考虑其余相关元素的变化情况，预测手段清晰明了。因此，自回归移动平均模型适用于指标较少的数据集的预测，这也是在预测本数据集中传染病传播人数时，自回归移动平均模型比一元线性回归算法准确率高的原因。

5 总结和展望

本文主要使用一元线性回归及自回归移动平均模型ARMA 对某传染病传播人数进行预测，通过实验可以发现，两种算法都可以进行预测。但是从预测值与真实值的误差来看，ARMA 模型的性能较好，其中有一天的误差率接近1%。这为接下来的传染病传播人数的预测提供了有力的依据。

下一步的目标是将本方法进行可视化界面设计，便于更多的人更好的了解未来传染病的传播情况，未雨绸缪，为可能发生的情况做好充分准备。