基于时空签到的移动社交网络关系推断

陶玉婷

（东华大学计算机科学与技术学院 上海市 201600）

1 概述

近些年，随着基于位置的服务和在线社交网络的流行，移动社交网络开始逐渐兴起，如Brightkite、Gowalla 等。在社交网络中，朋友关系是一项非常重要和敏感的信息，并可以用来进一步推断其他敏感信息。例如，通过用户的8 个朋友关系就可以推断其身份信息[1]。虽然已经有越来越多的社交网络用户意识到这一点，并且选择隐藏朋友关系信息（例如，Facebook 用户隐藏好友列表的比例从2010年的17.2%上升到2011年的56.2%[2]），但朋友关系信息仍存在其他泄露途径。

分享时空签到（check-in）数据，是移动社交网络中的关键用户行为之一。一方面，移动用户通过签到来完成社交行为；另一方面，服务商通过收集并分析用户签到信息，来改进用户服务、提升服务体验。然而，现有研究发现，由于朋友间在现实中的社交行为可能导致其拥有时空中相近的签到（例如，一同在餐厅用餐时，各自分享的签到），因此，用户的时空签到数据可被用于推断用户间朋友关系[3]。

本文提出了一种基于移动时空签到数据的朋友关系推断攻击方法。首先，通过分析移动轨迹中能够揭示用户朋友关系的个体移动模式和用户间的交互行为特征，构建用户间的时空关系矩阵；然后，通过自编码器实现时空关系矩阵的向量化；最后，依据编码的时空关系向量实现朋友关系的推断攻击。

2 研究背景

基于移动数据的朋友关系推断研究主要是从数据挖掘的角度，根据某些观察抽取有效特征进行朋友关系推断。因此，从用户的移动数据中抽取与朋友关系具有强相关的移动特征是至关重要的。该特征能够有效地区别朋友关系对和非朋友关系对，满足若两个用户的时空交互越频繁或移动轨迹相似，则他们具有朋友关系这一条件。

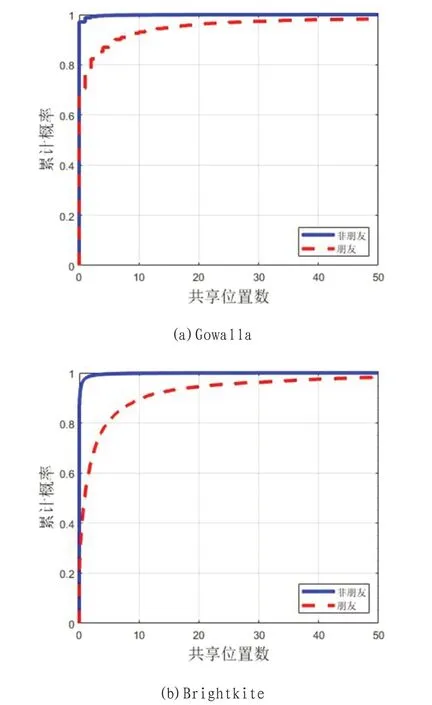
图1：朋友与非朋友间共享位置数累计概率分布图

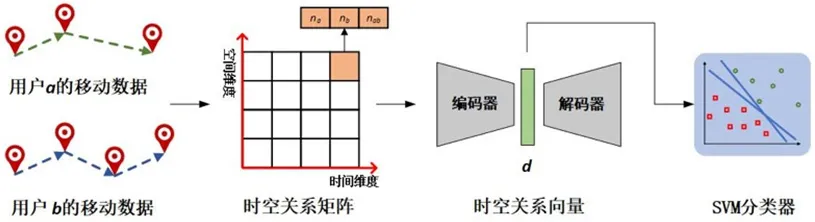
图2：朋友关系推断攻击模型结构图

文献[3]从移动数据中抽取用户的访问路径和停留地点集合，并用分层图来表示这些地点，如果用户在较低层共享更多的地点，则认为他们之间的相似程度更高，更有可能是朋友。该方法仅使用用户个体的移动模式未考虑到用户间的交互移动特征。文献[4]发现两个人的碰面事件是判断他们是否是朋友的一个很有力的指示因子。另外，如果该事件发生在非工作时间或者是非工作地点，他们是朋友的概率更大。在文献[4]的基础上，文献[5]发现碰面事件涉及到的地点数越多，他们是朋友的可能性越大。与之前工作不同，文献[6]从签到数据中提取众多有效的特征，包括共同出现地点集的时间和空间范围、地点的多样性和特征性和社交关系网的结构特征等，再将这些特征应用到多种机器学习技术推断用户对之间是否具有朋友关系。和文献[6]类似，文献[7]运用逻辑回归二元分类器预测用户对之间是否存在朋友关系，与文献[6]不同的是该工作仅仅考虑两个个体碰面次数这一个特征。这些方法均基于用户间共享位置或发生碰面这一假设，无法推断那些从未共享过位置的用户对关系推断。

针对上述问题，本文综合个体移动模式和用户间的交互行为来构建时空关系矩阵。一方面，该时空关系矩阵能够有效推断用户间是否存在朋友关系；另一方面，利用时空关系矩阵中的个体移动特征可以推断不存在时空交互的用户是否存在朋友关系，有效地解决了现有推断方法适用性不普遍的问题。

表1：符号定义

表2：数据集统计信息

3 基本定义与问题描述

3.1 符号说明

用户的移动数据是若干条签到记录的集合，其中每条签到信息可以定义为一个三元组(u,p,t)∈U×P×T，该三元组表示在t 时刻用户u 位于位置p。签到数据集合中涉及到的所有用户用集合U={u1,u2,...,un}来表示，其中n 表示该移动数据中包含的用户个数。此外，本文使用集合T={t1,t2,...,tn}来表示移动数据中所有签到的时刻集合。因此，用户u 的移动轨迹T 可以用一系列签到表示为Tu=〈(u,p1,t1),(u,p2,t2),...,(u,pn,tm)〉,其中tj≤tj+1(1 ≤j ≤n)。上述符号的定义如表1所示。

3.2 共享位置与共享位置数

定义（共享位置）给定两个用户u1∈U 和u2∈U 的移动轨迹 和当且仅当存在使得pm=p 且pn=p，则称p 为用户u1和u2的共享位置。

用户u1和u2移动数据的共享位置数其中表示用户u1移动数据中的所有为位置集合，表示用户u2移动数据中的所有位置集合。

3.3 朋友关系推断攻击

定义（朋友关系推断攻击）给定一组用户U 以及他们在一段时间内的移动轨迹TU，对于U 中的每一对用户(ua,ub)的移动轨迹均可以通过攻击模型f 推断他们之间是否存在朋友关系。其中攻击模型f 满足：

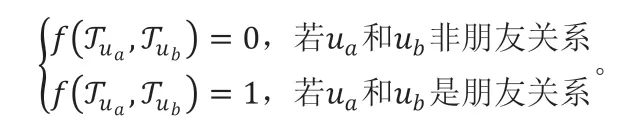
4 实验数据集分析

为了有效地表征用户对的交互行为，本节基于实验数据集对用户间的共享位置数与朋友关系的相关性进行了探究。

4.1 数据集概述

本文使用公开的基于位置服务社交网络平台收集到的Gowalla数据集和Brightkite 数据集，且每个数据集均包含签到数据集和社交网络图两个部分的数据。其中每条签到记录的格式为：

＜userID，time，placeID，longitude，latitude＞

对数据集中两个数据集的具体信息如表2所示。

4.2 共享位置数与朋友关系相关性分析

针对上述数据集进行朋友关系与共享位置数之间关系的探究。将用户集合U 中的所有用户两两配对，形成若干组无序的用户对(ui,uj),其中ui∈U 且uj∈U。所有的用户对根据社交网络图分成朋友关系和非朋友关系两类分别统计每类用户对的共享位置数，并绘制其累计概率分布图。如图1所示，Gowalla 数据集中的非朋友关系对中有近98%用户间从未共享过位置，而朋友关系中仅有约60%；Brightkite 数据集中，非朋友关系中有近97%的关系对从未共享过位置，而朋友关系中仅有35%左右未共享过位置。由此可见，非朋友关系大概率不存在共享位置，而朋友关系则更倾向于具有共享的位置。因此，用户对是否共享过位置以及共享位置的数目可以成为本文推断用户对之间是否存在朋友关系的一个重要特征。

5 朋友关系推断攻击

由上节分析可知，共享位置数是表征一对用户间是否存在朋友关系的一个重要指标，但仅使用该指标无法推断不存在共享位置的用户对。针对该问题，本文首先综合用户个体的移动模式和用户间的交互特征构建用户对的时空关系矩阵，然后使用自编码器将时空关系矩阵压缩，使得到的时空关系特征向量尽可能包含了原矩阵中的信息，最后通过分类器（例如，支持向量机）进行朋友关系推测。具体的攻击模型结构如图2所示。

5.1 时空关系矩阵的构建

首先，基于经纬度将位置集合P 映射到I×J 个方格中，时间集合T 分为M 个时长均为τ 的时间片段，将用户的移动轨迹重构成I×J×M 的时空立方体，使得每一个签到记录均可投放到该立方体中的某个小立方体中，记作表示时空立方体中第m 个时间片段的第i 个纬度部分和第j 个经度部分。

定义（时空关系矩阵）给定两个用户ua和ub的移动轨迹和将轨迹中的签到投射到I×J×M 的时空立方体中，则用户对(ua,ub)的时空关系矩阵

其中na为中用户ua的签到数，nb为中用户ub的签到数，

na,b为中用户ua和ub的共享位置数。

空间位置的划分方法是在二维位置平面通过多次四等份切割保证每个方格中的兴趣点个数不超过一定的阈值σ。由此可见，时空关系矩阵的稀疏程度是由划分时空立方体的参数σ 和τ 决定的。通常，参数σ 和τ 越小，构建的时空关系矩阵会稀疏，抽取到的移动特征就会越模糊，因此合理的选择参数σ 和τ 也是本文实验过程的一个重要部分。

5.2 时空关系矩阵的编码

由于构建的用户对时空关系矩阵O(a,b)是一个高维度的矩阵，其中包含很多无关的特征，为了更加准确地抽取到用户的移动特征，本文利用自编码器模型[8]对O(a,b)进行向量化的表示。

给定一个时空关系矩阵O(a,b)，首先送入有R 个隐藏层的编码器中，然后将编码器的输出作为解码器（与编码器具有相同的结构）的输入，解码器尽可能得到一个与编码器输入O(a,b)一致的结果该过程就是自编码器（记作A）的整个工作过程，该网络中的第r 层输出结果可以表示为：

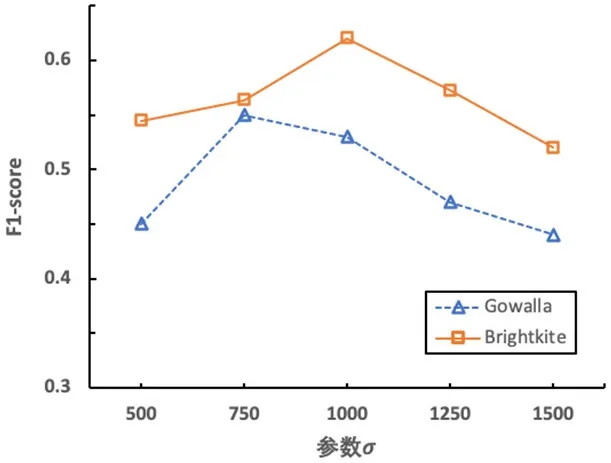
图3：不同σ 值对攻击结果的影响

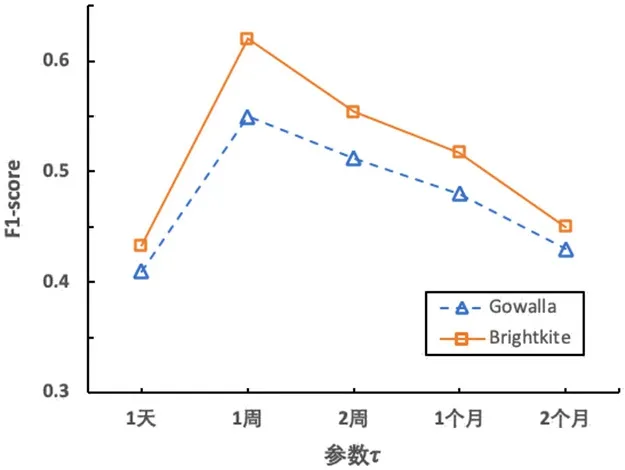
图4：不同τ 值对攻击结果的影响

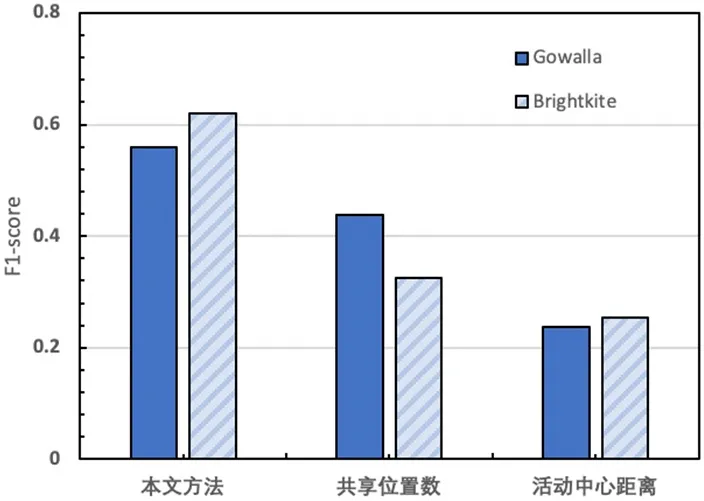
图5：朋友关系推断攻击结果对比图

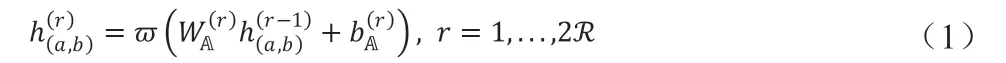
由编码器和解码器共同组成的自编码器通过最小化重构误差L学习网络中的参数和其中损失函数L 的定义如下[10]：

5.3 朋友关系推断攻击

6 实验结果与分析

6.1 实验方案

6.1.1 实验参数设置

实验中，编码器网络的每一个隐含层神经元的个数均为前一个隐含层神经元个数的一半，最后一个输出层神经元的个数为固定的个数d为128。分类器为SVM模型，其中核函数为径向基函数(Radial Basis Function,RBF)。实验选择70%的用户对数据进行训练，30%的用户对数据进行测试。

6.1.2 对比方法

本文选择了两种现有朋友关系推断模型进行攻击性能的对比：

共享位置数法[9]：该方法通过计算每对用户之间共享的位置数作为衡量他们是否具有朋友关系的知识因子。然后通过SVM 对该特证进行学习，从而实现利用共享位置数推断朋友关系的功能。

活动中心距离法[10]：该方法将用户签到数据中位置集合的几何中心作为用户活动的中心，然后计算每个用户对活动中心之间的欧式距离，将该距离作为训练SVM 分类器的特征。

6.1.3 评价指标

本文选择F1 值作为衡量指标，定义如下：

6.2 参数σ对攻击结果的影响

本节研究构建时空关系矩阵过程中空间粒度σ 对推断结果的影响。实验评估了500、750、1000、1250 和1500 五种情况下的推断结果。实验结果如图3所示，在Gowalla 中，当σ=750 时F1-score达到最大值56%；而在Brighkite 中，σ=1000 时F1-score 达到最大值62%。这是数据集中位置分布特征决定，当位置越分散时，参数σ 取较小值才能较为准确地表达用户的移动特征。

另一方面，实验结果表明σ 的过小或过大均不利于朋友关系的推测，这是因为σ 过小导致时空关系矩阵稀疏，难以表达用户的移动特征；而σ 越大导致时空关系矩阵种包含过多的噪声，即偶然事件。

6.3 参数τ对攻击结果的影响

本节研究构建时空关系矩阵过程中时间粒度τ 对推断结果的影响。实验评估了1 天、1 周、2 周、1 个月和两个月五种情况下的推断结果。实验结果如图4所示，当τ 为一周时两个数据集均达到了最优攻击结果，这是由于人们的日常生活规律一般是以周为活动周期的。

与参数σ 具有相似的规律，即推断攻击结果的准确性随着时间粒度τ 的增大先增加再减小。这是由于粗粒度时间片段包含较多的噪音，而细粒度时间片段不易捕获用户之间有效的移动特征。

6.4 朋友关系推断攻击结果

基于上述实验结果，本文选择最佳的参数即τ=7，σ= 750（Gowalla）或1000（Brightkite）进行实验，并与两种基本模型进行对比。实验结果如图5所示，在两个数据集上，本文提出的方法均优于共享位置数方法和活动中心距离方法，其中Brigthkite 数据集中本文方法的F1-score 分别提高了37%和30%；Gowalla 数据集中分别提高了12%和32%。

7 结束语

本文就基于移动轨迹推断朋友关系这一问题，提出一种新的朋友关系推断攻击方法，该方法通过综合用户间的交互特征和用户个体的移动模式推断用户间是否存在朋友关系。本文提出的攻击方法具有较高的推断准确性，适用于未共享位置用户间的朋友关系推断。使用Gowalla 和Brighkite 两个基于位置社交网络的数据集验证了所提出朋友关系推断攻击模型的有效性。实验结果表明，两个数据集推断结果的F1-score 分别达到了56%和62%。未来工作将针对这类攻击方法提出合理有效的防御机制。