基于回归算法的政务服务中心大厅办事业务量预测分析

李林

（福建省经济信息中心 福建省福州市 350003）

1 引言

政务服务中心已日益成为各地方政府面向群众提供政务服务的重要平台。政务服务应更加关注群众体验感，服务水平绩效应该由群众来评判。科学合理地预测到政务服务中心的办事业务量，能够有效地辅助政务服务中心管理人员进行决策，科学高效地调派窗口工作人员。通过弹性的增减办事窗口工作人员，能够有效降低群众办事现场等待时间，提高办事效率，进而提升办事群众的体验感，节约行政资源。

从政务服务中心大厅业务量的周期性、随机性出发，结合业务量数据变化的非线性和非平稳的统计特征，预测问题本质上是运用机器学习方法，对数据回归问题进行研究，因此可以采用回归算法进行数据处理。利用算法模型来解决问题，需要通过实验数据论证不同算法的预测效果。即从文件中读取出某一个部门每一天办理的业务数量，利用回归根据日期来预测当天的业务办理数量，从而使相关部门可以提前进行人力部署。结合客流预测分析特点，以及当前常用回归算法，选用多项式回归算法、KNN 回归算法、GBRT回归算法、Bagging 回归算法这四种进行拟合比较。

2 回归算法分析

回归算法是一种预测性的建模技术，它研究的是因变量（目标）和自变量（预测器）之间的关系。通过计算能够完成新数据自变量与因变量的关系推导，因此回归算法能够实现预测操作，在数据预测方面具有良好表现。利用算法模型来解决问题，需要通过实验数据论证不同算法的预测效果。[1]适合客流预测的回归算法包括多项式回归、KNN 回归、GBRT 回归、Bagging 回归等。

机器学习的处理过程为：首先数据预处理，提取数据库中的数据标签或初始数据，并将数据分为训练集和测试集；其次模型学习，利用训练集数据运用学习算法进行训练；再次评估模型，经过训练建立最终模型Final Model，使用测试集数据对最终算法模型进行测试，根据测试结果对最终模型进行评估，依据评估结果再调整最终模型；最后新样本测试，最终模型通过新样本再进行训练后，通过对模型进行调整最终达到最佳判定效果。如图1所示。

3 样本选取

以某大型城市中进驻当地政务服务中心大厅的某区市场监管局2019年的每日业务量为例，选取该局2019年全年办件情况数据，采取五折交叉验证的形式进行训练及模型性能评估。即将整个数据集平均划分成五等份，选取其中四份作为训练集，一份测试集，循环执行五次并记录结果。

训练环境选择上，操作系统使用Intel(R) Core(TM) i7-6700 CPU @ 3.40，内存16.0 G，软件工具为pycharm，编程语言使用python，工具包包括Numpy、Pandas、Scikit-learn 和Matplotlib。

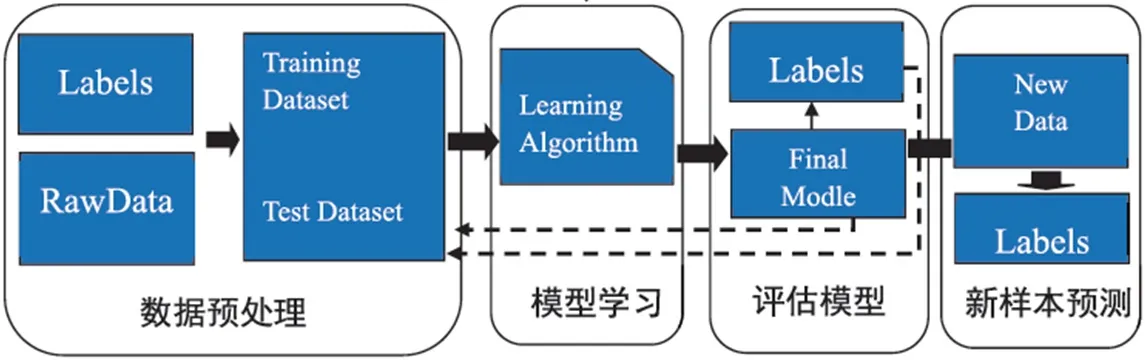
图1：机器学习原理流程图

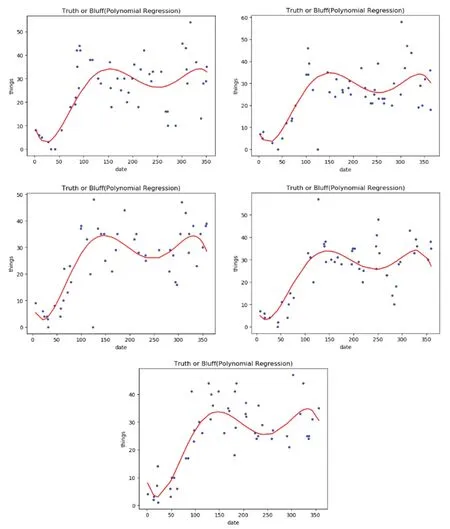
图2

处理过程首先读取文件，取某区市场监管局办件数据，将申报时间只保留日期，然后保存为新增一列为日期；按照日期统计事件数，统计每日申请事件数量，过滤掉节假日，导入scikit-learn 相应的包以及maplotlib.pyplot，再进行特征处理，从而定义回归模型；最后训练模型并画图，然后计算指标。

4 实验与分析

4.1 多项式回归算法

多项式回归即用一个含有多项式的曲线去拟合数据集中特征和预测值成非线性关系的数据点，从而训练得到这条多项式曲线进行相应的预测，表达式如下[2]：

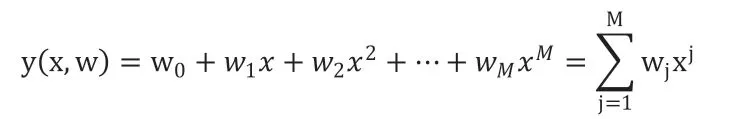
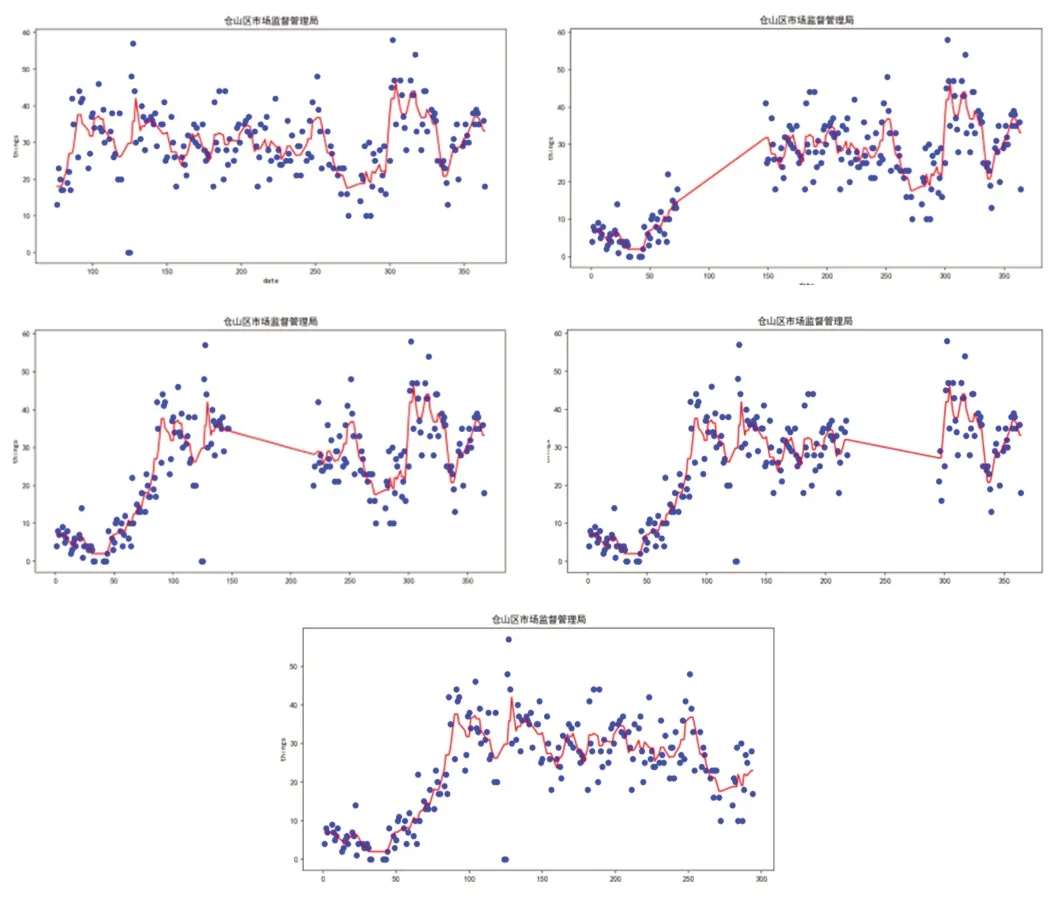
图3

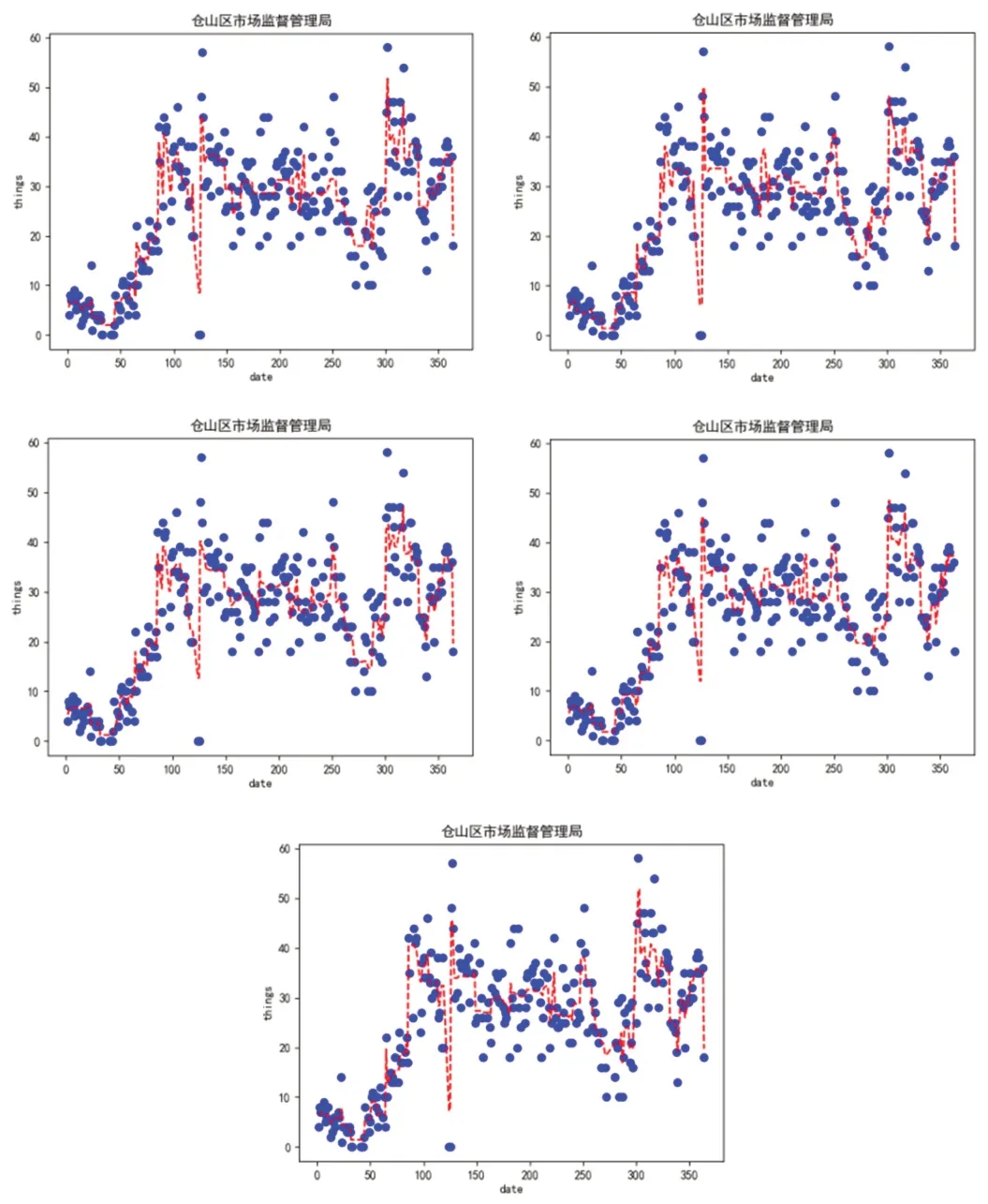
图4

结合给定的数据集采用最小二乘法对该多项式进行训练，获取其参数从而对未知的数据进行预测。通过五折交叉验证的形式，得出五次多项式拟合验证图如图2所示。

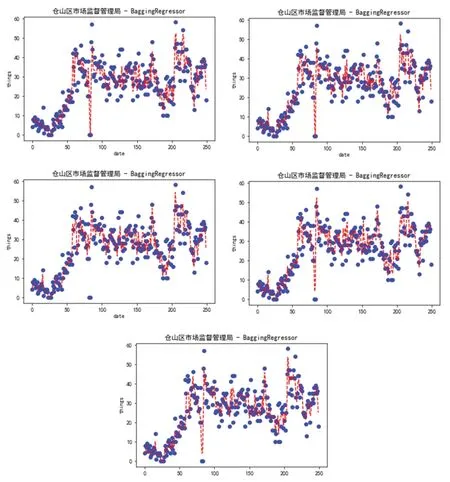
图5

某区市场监察管理局五折交叉验证结果MAE 误差分别是7.639113，6.479720，6.087571，5.789480，5.384119。以平均绝对误差MAE 为准，调整多项式次数实验结果对比如表1所示。

根据多项式的性质，选择5 次多项式到10 次多项式。1-4 次曲线拟合的效果较差，10次以上容易造成严重的过拟合现象，所以5-10次效果较为客观。结合以上实验结果可知，在七次多项式时误差达到最小，为5.33655，表示实际结果比预测结果平均每天会有5 左右办理件数的差距。

4.2 Knn回归算法

Knn 算法全称是k 近邻算法，就是指最接近的k 个邻居（数据），即每个样本都可以由它的k 个邻居来表达。表达式如下：

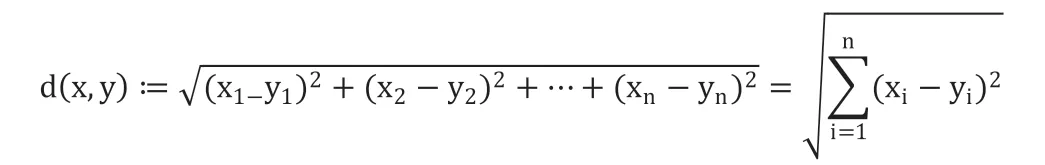
Knn 算法的核心思想是在一个含未知样本的空间，可以根据离这个样本最近邻的k 个样本的数据值来确定样本的数据值。[3]Knn算法应用于回归算法，一般采取平均值法。即假设要预测一个样本的值，首先观察目标样本周围的其他样本的平均值，通常认为平均值就是目标样本的值。所以Knn 算法一个比较重要的点是k 值的选择，k 值选择过小，容易导致过拟合，k 值选择过大会导致模型简单，预测失误。

选择某区市场监管局2019年数据进行Knn 回归预测，在k=5的情况下5 折交叉验证情况下的拟合情况图如图3所示。

使用5 折交叉验证对数据进行回归预测，得到的MAE 值分别为：11.48、12.096、6.15599、6.596、11.96，平均值为9.6576，表示实际结果比预测结果平均每天会有9 到10 件办理件数的差距。以下为在不同k 值设置下的MAE 值的结果比较，通过不同k 值的取值得到的效果来看，对于k 值取得3 至5 的效果是较好的。如表2所示。

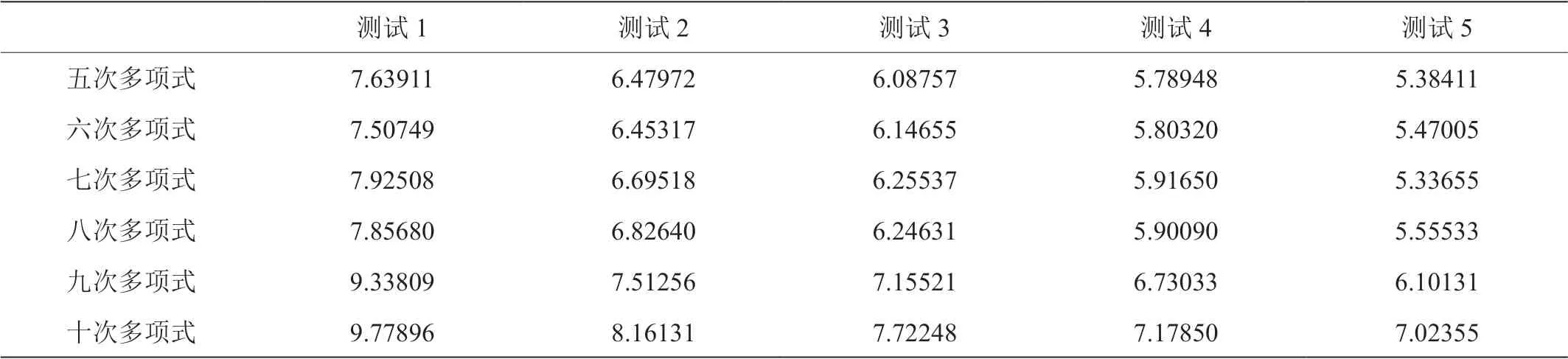
表1：多项式次数误差表

表2：KNN 回归误差表

表3：GBRTmax_depth 取值误差表

表4：Bagging 基学习器误差表

4.3 GBRT回归算法

GBRT 全称是梯度提升回归树，是对于任意的可微损失函数的提升算法的泛化。GBRT 是一种集成方法，通过合并多个决策树来构建一个更为强大的模型。与随机森林方法不同，梯度提升采用连续的方式构造树，每棵树都试图纠正前一棵树的错误。默认情况下，梯度提升回归树中没有随机化，而是用到了强预剪枝。梯度提升树通常使用深度很小的数，这样模型占用内存更少，预测速度也更快。其优点在于对异构特性数据的自然处理，强大的预测能力以及在输出空间中对异常点的鲁棒性。[4]其表达式如下：

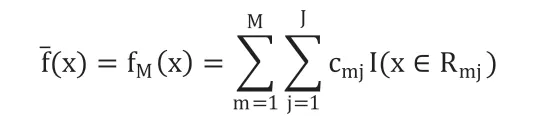
以下为GBRT 最高树高为3 的情况下5 折交叉验证情况下的拟合情况图。使用随机5 折交叉验证对数据进行回归预测，得到的MAE 值分别为：3.153299、3.615895、3.346077、3.395009、3.301559，平均值为3.362368。如图4所示。

以下为在不同最高树高值设置下的MAE 值的结果比较。通过对5 折交叉验证的MAE 值来看，其MAE 值能够达到2.2704，表示实际结果比预测结果平均每天仅有2 件左右办理件数的差距。综合不同max_depth 值所消耗的资源与所得到的效果来看，较大的max_depth 会在一定程度上增加时间开支和导致过拟合问题。因此对于max_depth 的取值，在3～5 的效果是较好的。如表3所示。

4.4 Bagging回归算法

Bagging 是最常见的集成学习框架之一。假设有一个数据集D，使用Bootstrap sample（有放回的随机采样）的方法取了k 个数据子集（子集样本数都相等）作为新的训练集，对于回归来说，新的观测值可以通过众多决策树得到很多预测值，最终结果就是这些预测值的简单平均。因为Bagging 仅仅是作为一种集成学习框架，因此就本质而言Bagging 回归算法的原理取决于其所采用的基学习器。这里使用的基学习器为决策树。回归决策树主要指CART（classification and regression tree）算法，内部结点特征的取值为“是”和“否”，为二叉树结构。所谓回归，就是根据特征向量来决定对应的输出值。回归树就是将特征空间划分成若干单元，每一个划分单元有一个特定的输出。因为每个结点都是“是”和“否”的判断，所以划分的边界是平行于坐标轴的。对于测试数据，只要按照特征将其归到某个单元，便得到对应的输出值。[5]CART 回归树表达式如下：

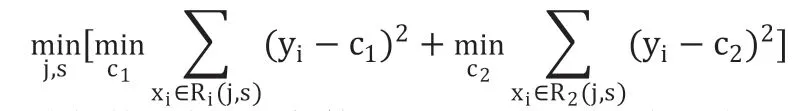
选择某区市场监督管理局进行Bagging 的回归预测，以下为5折交叉验证情况下的拟合情况图。使用随机5 折交叉验证对数据进行回归预测，得到的MAE 值分别为：3.0176,2.82,2.96,2.6612,2.858，平均值为2.86336。如图5所示。

在不同基学习器设置下的三个部分的MAE 值的结果比较。通过5 折交叉验证的MAE 值得结果来看，其MAE 值达到2.8244，表示实际结果比预测结果平均每天会有2 到3 件左右办理件数的差距。如表4所示。

5 预测结论

MAE（平均绝对误差）越小越好，越小说明预测的结果越准确。从表1、表2、表3、表4 实验结果可以得到：MAE 依次为5.33655、9.6576、2.2704、2.8244。由于业务量数据受到许多不确定性因素的影响，因此预测出来的办事量数据不可能和真实的数据完全一致，这时就需要进行误差分析，分析预测后的业务量数据是否在允许的误差范围内，本实验采用绝对误差分析的方法。通过表1、表2、表3、表4 中的误差结果计算得出，办事流量预测的平均绝对误差在2 件到10 件之间。尤其通过建立GBRT 回归模型，预测数据已经非常接近实际情况，可以对办事流量进行预测，并且具有较好的可参考性。

6 结束语

数据实验结果表明，GBRT 回归算法能够有效地对政务服务中心大厅业务量进行预测，为实际应用中的客流预测问题提供了良好的方法。本文对四种模型进行了构建，并进行学习和训练，利用进驻大厅的某区市场监管局2019年每日办件数量对预测模型进行检验。通过多项式回归、KNN 回归、GBRT 回归、Bagging 回归这4种预测模型进行仿真，结果表明，基于GBRT 回归的办事业务量模型的预测误差最小。因此，该预测模型可为政务服务中心大厅业务量的预测提供较好的参考，有助于政务服务中心效能提升。此外，为了更好地提高预测准确性，需要对残差进行详细分析，对于最大深度max_depth 的利用将是GBRT 回归算法下一步要研究的问题。