基于K-means算法的亚洲足球聚类研究

孙鹏 杨杉

（四川大学锦城学院 四川省成都市 611731）

1 前言

大数据时代的到来，让数据的处理、分析及挖掘成为了人们热衷于研究的一大课题，各行各业都能通过数据挖掘从数据源中探寻出许多有用的潜在知识，而我们在进行数据挖掘之前通常还会对数据进行探索、预处理等一系列操作来对我们之后的工作奠定基础。数据挖掘的主要方法有：分类、聚类、关联分析、回归预测。本文所使用到的K-means 算法就是一种无监督学习的聚类算法，它是用于将数据划分成不同的分组的方法。

1.1 研究背景

足球起源于中国古代的“蹴鞠”。1958年7月，前国际足联主席阿维兰热访华时说，足球运动最初起源于中国。他的这一说法于2004年得到了国际足联的正式确认[1]。亚足联自1954年成立以来，现有46 个会员协会和1 个准会员协会[2]。亚洲足球在世界范围内水平较弱，身处亚洲的我国在足球方面的成绩也往往不理想，常常受到外界诟病。而为了客观地反映国足在亚洲的真实水平，本文通过K-means 算法，来对亚洲各个球队的排名进行一个聚类研究，将亚洲球队的排名数据进行一个档次的划分，以此来观察中国足球到底在亚洲层面属于哪一档次的球队。

1.2 研究意义及方法

本文利用《虎扑体育》等专业足球网站收集和整理到了24 支进入到2019年阿联酋亚洲杯决赛圈的亚洲主流球队的2020FIFA 排名、2019年亚洲杯排名以及2015年亚洲杯的排名，利用K-means算法进行聚类研究，在大数据的剖析下客观地反映国足在亚洲足坛的一个真实地位。

2 数据探索及预处理

2.1 数据特征

收集整理了24 支亚洲主流球队2020FIFA 排名，2019年亚洲杯排名以及2015年亚洲杯的排名，首先从描述性统计结果看，FIFA 排名最高为28 名，仅仅刚踏入世界杯32 强的门槛而已，这也反映了在世界范围内亚洲足球整体处于非常落后的局势。而2015年的亚洲杯有9 项缺失值，造成这一缺失的原因是首先2019年亚洲杯首次进行进行了扩军，从历年的16 支增加到了24 支，而四年间各个国家的足球水平有着起伏，导致了某些球队不一定都进入到了这两届亚洲杯的决赛圈，所以没有排名。

2.2 相关性分析

person 相关系数是一种准确度量两个变量之间的关系密切程度的统计学方法[3]。这里利用corr 函数计算person 相关性，得到了2020FIFA 排名与2019 亚洲杯排名的person 相关系数接近0.8，具有显著的相关性。而将它们建立回归模型，从图1 中可以看到是呈现一个显著的正向的线性关系。

2.3 数据预处理

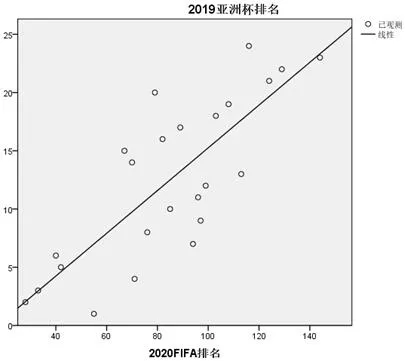
图1：线性回归模型

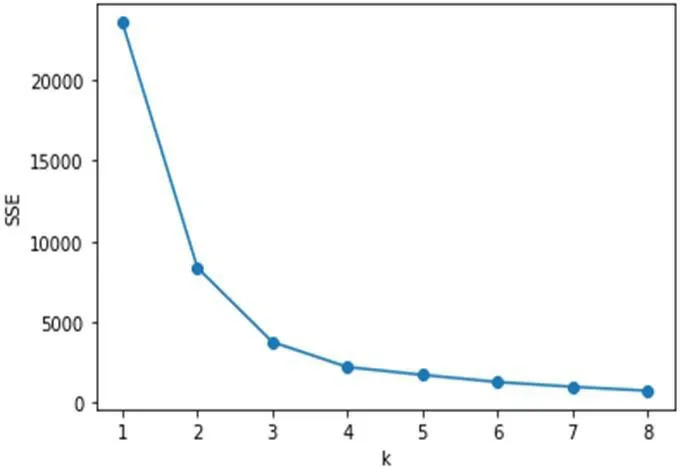
图2：“手肘”法折线图

针对2015年亚洲杯排名中9 项缺失的数据，由于本届亚洲杯决赛圈只有16 支球队参加，所以其余未进入球队的名次这里利用pandas 中的fillna 函数进行填充，将没有进入到2015 亚洲杯决赛圈的球队填充为17 名。

而由于k-means 算法采用距离度量相似度，需要做数据规范化，这里使用了Z-score 标准化[4]方法，消除因不同量纲级别而引起的误差。

3 K-means聚类算法

3.1 K-means聚类算法概况

K-means 算法，是在1967年，由MacQueen J 提出的，一种用于对数据进行聚类的算法[5]，由于K-means 算法具有简单且较为容易实现的特征，因此得到了各界的广泛应用。K-means 算法采用的是划分法聚类技术，一般来说用于p 维度连续空间中的对象聚类。该距离是用来作为相似性的评估指标，即，两个对象之间的距离越接近，相似性就越大。

3.2 K-means聚类算法基本流程

K-means 算法是一种无监督学习的算法，它的大致流程为：

1.随机的选择k 个数据集合中的对象作为初始簇的中心点；

2.对数据集合当中的所有对象进行遍历，按照它们之间的相似性来判断每一个数据对象应该被分配到哪个簇当中去。相似性一般用数据对象与聚类中心点之间的欧几里得距离（即欧式距离）来衡量。距离越小，说明数据对象和聚类之间的相似性就越大。最后将数据对象分配到相似性最大的集群；

3.将每组中非中心点到聚类中心的平均值计算出来，然后作为新的聚类中心

4.将上述的步骤2 和步骤3 一直重复进行，直到簇中心没有改变或已经达到最大迭代次数。

3.3 欧氏距离

前文中提到了利用欧氏距离计算非中心点到中心点之间的距离，这是一种常见的用于度量空间中两点之间距离的度量方式，欧氏距离公式为：

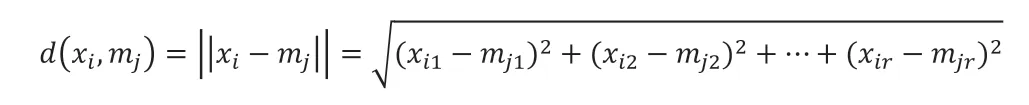
4 最佳K值的选择

4.1 K-means算法的缺陷

尽管K-means 算法具有简单性和高效性的优点，但它也有缺点。K-means 算法通常存在两类难以解决的问题：一是如何选择合适的对象，作为初始的聚类中心；二是怎样在一开始就把合适的k 值确定下来[6]。除此之外，研究者们还提出了不少改进的K-means 算法，例如：Likas 和Vlassis 提出了全局的K-means 算法，该算法是一种有效的基于递增思想的全局优化方法，不依赖于任何初始参数[7]。优化了初始类簇中心，能够得到全局最优解。但是，数据集中的簇数，仍然需要输入；Likas 和Tzortzis 共同提出了最小最大K-means 聚类算法，该算法以欧式距离为基础，聚类中心是选取了尽可能远的样本点，在选取初始值时，规避了可能会发生的聚类中心太过邻近的这种情况，而且提高了划分初始数据集的效率[8]。传统的K-means算法在通过以上改进的K-means 算法后在一定程度上弥补了某些方面的不足之处，取得了较为不错的聚类效果。但是迄今为止，K-means算法仍然没有一个合理的解决方法来同时解决自动确定初始k 值和选择合适的初始聚类中心这两个核心问题。

4.2 利用“手肘”法获取最佳k值

“手肘”法是一种确认最优k 值的方法，它利用的是SSE 和k值的关系图来判断的[9]。手肘法的主要思想为：在K-means 算法下，当一个数据集进行聚类时，随着k 的值增大，会把数据集分割得越来越详细，聚类的中心不断增多，SSE 逐渐减小。当k 值小于真实的簇数时，随着k 值继续增加，SSE 值的下降率相对较大，关系图显示两点之间的线会更陡。当k 与真实聚类数相等时，随着k 值的增大，SSE 值下降的速度会越来越慢，关系图显示两点之间的线会变得平缓[10]。因此，SSE 值和k 值的图形是一个类似“手肘型”的折线图，拐点处的值（即位于“肘部”的临界点的值）是最佳k 值。如图2所示，k=3 即为折线图的拐点，因此对于此数据集，最佳簇数为3。

5 研究结果

由“手肘”法得出的最佳聚类数k=3 放入模型中，开始对数据集进行聚类：

data=df.iloc[:,1:]

kmeans=KMeans(n_clusters=3)

kmeans.fit(data)

kmeans.predict(data)

y_=kmeans.fit_predict(data)

最后通过聚类得出的结果：[日本，韩国，伊朗，澳大利亚，卡塔尔]为一梯队；[阿联酋，越南，中国，约旦，乌兹别克斯坦，吉尔吉斯斯坦，巴林，伊拉克，沙特，阿曼，黎巴嫩，叙利亚]为一梯队；[泰国，巴勒斯坦，印度，菲律宾，土库曼斯坦，也门，朝鲜]为一梯队；所以，在经过K-means 聚类算法研究后，客观上来说，中国足球在亚洲足坛中，虽然比不上日本、韩国、伊朗、澳大利亚、卡塔尔这些一流球队，但是再不济也是属于亚洲第二档实力的球队，并没有外界所贬低的那么差，并且近期国足利用国际足联规则归化了一批巴西籍球员，整体实力有所提升，我相信中国足球能够继续进步，冲出亚洲，走向世界！