一种QPSK中的频偏校正方法
孙腾 苑春雷 马守兴
(中国电子科技集团公司第五十四研究所 河北省石家庄市 050081)
QPSK作为PSK相位调制的一种[1],具有稳定的包络、误码率低、传输高效、易于实现等优点,在地面数字移动通信系统、卫星通信系统中被广泛应用。在QPSK 数字调制解调通信系统中,主要包含调制、解调、成型滤波、匹配滤波、纠错编码、纠错译码、定时同步、载波同步、信道估计、信道均衡等主要技术。经典的QPSK 解调原理中,载波同步方法主要为导频法、costas 环法、平方环法,随着通信技术的发展频谱资源紧缺、突发通信使用场景更广泛,接收机架构由超外差结构向零中频架构转变,经典的载波同步方法逐渐被淘汰。突发通信中,可以通过插入导频序列实现快速载波同步[4][5],本文设计并实现了一种载波同步中的频偏校正方法,通过已知序列块直接计算出一定时间间隔内的载波相位旋转值并校正,更适用于零中频接收机中突发通信的快速载波同步。
1 频偏校正
1.1 QPSK调制解调
QPSK 为四进制相位调制和正交幅度调制,每个载波相位携带2bit 信息,根据信息序列不同,分布在2π 区间。
如表1 所示,在QPSK 调制中编码映射决定着载波相位变化状况,相位映射表采用格雷码的编码方式。二进制的变化只存在一位,不存在π 相位的突变,可以减少最终判决后的误码率[2]。
根据信息相位映射关系图可以得到QPSK 调制表达式。
发信号表达式为:

其中ωc为载波角速率,sl(t)为基带信号:

展开三角表达式为:

其中I(t)与Q(t)为串并变换后信息序列
由上式可得QPSK 调制框图,如图1 所示。
接收端分别用正交载波cos ωc't 、 sin ωc't 解调接收到的信号,ω'c为本地产生载波角速率,通过低通滤波器后,可以得到:
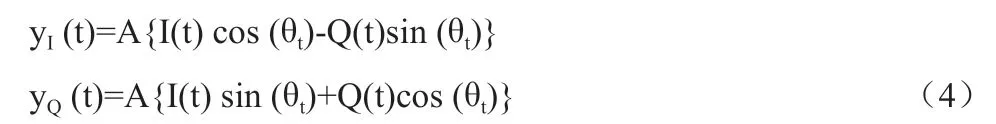
其中:
A 为经过信道和接收正交下变频后的信号强度信息,θt为下边片后瞬时残余相位角:
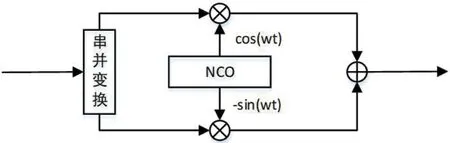
图1:QPSK 调制简易框图

图2:频偏估计误差仿真图

图3:迭代残差仿真图

Δ ω 为残余载波角速率,即频偏角速率。
对IQ 两路的低通表达式合并,归一化后,可表达成复数形式:


表1:QPSK 相位映射表
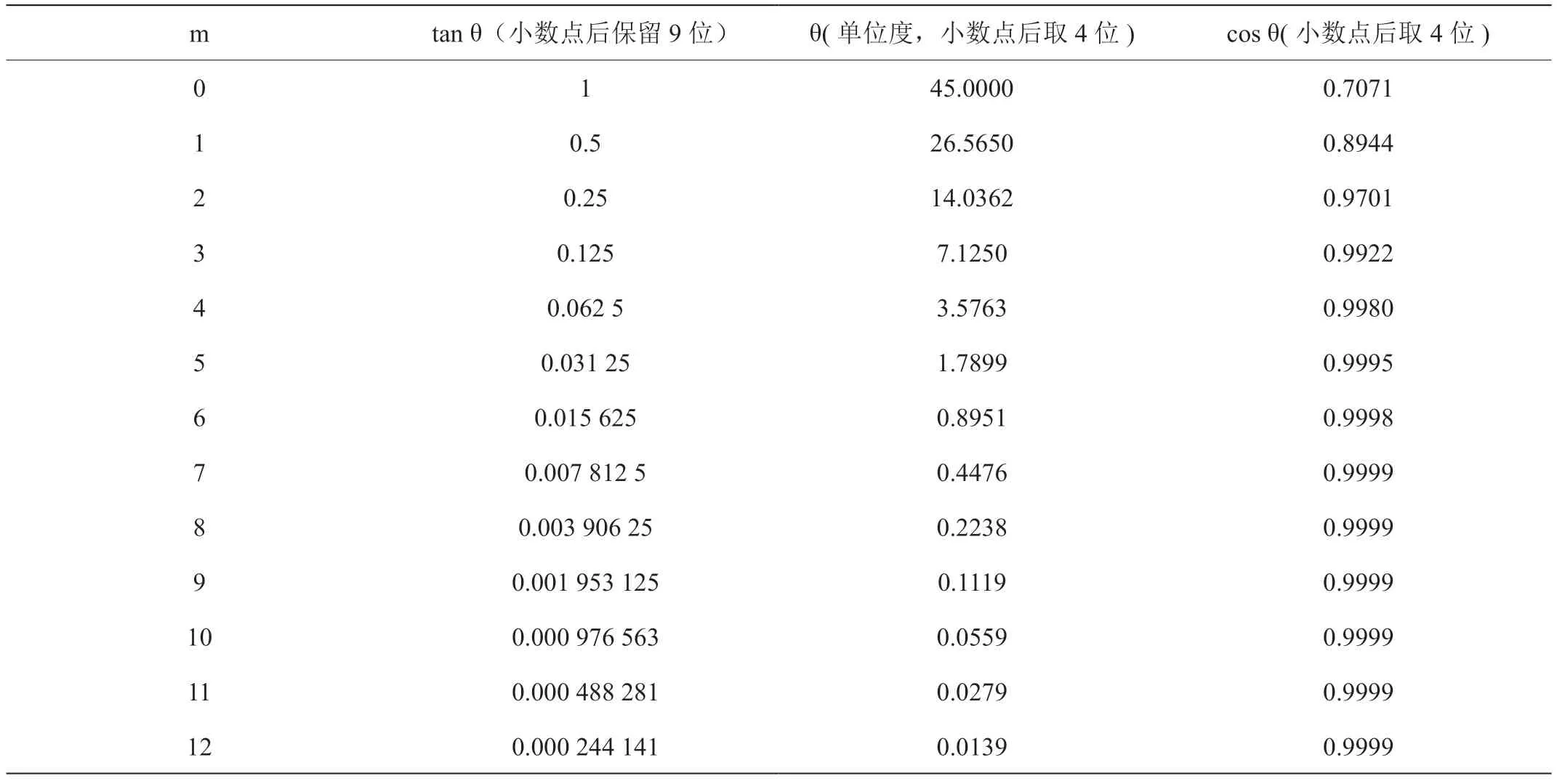
表2:旋转迭代角度表
恢复IQ 的基带信息需要计算θt,即可恢复出基带信号。

1.2 频偏估计
经过分析,正确解调QPSK 信号需要消除载波影响,恢复出原始基带信息。为了快速估计出残余频偏,通过已知序列,根据序列特性可以快速计算出频偏值[4]。任意间隔一定时间的同一已知序列做相关运算均可估计出限定范围的频偏,频偏估计范围跟序列间隔长短有关。在接收端已完成定时同步后,进行下面计算。
发射序列中需满足如下序列段为{Xp1, Xd, Xp2},其中:

Xp1与Xp2相同可视作训练序列;
Xd为间隔序列,n,d 的取值大小决定估计的频偏范围;长度n 可根据具体情况选取,n 越长计算结果受噪声影响越小。
由接收端表达式,Xp1与Xp2可表示为:

设θp11=θ1,可知

将Xp1与Xp2共轭相乘,可得
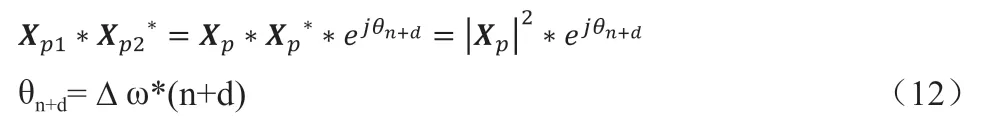
因θ 以2π 为周期,所以当θ 的值超出2π 区间,取值将不唯一。限定取值范围:

可得:

通过上式,由实际码速率可以得到可测残余角速率范围,fs为符号速率,频偏为

当n=1,d=0 时,可得最大频偏检测范围-fs/2 到fs/2,此时紧邻两个符号共轭相乘计算频偏。实际当中n 取值越大,计算结果受噪声影响越小。

根据上述分析进行了MATLAB 仿真计算,设置了d=128,频偏为符号速率的1/3000,Xp分别设置为[2 4 8 16 32 64 128 256 512]的随机序列,信噪比分别为[7 10 15 30]。由仿真结果可以看出,估计精度受序列长度,信噪比影响。序列越长、信噪比越高,估计误差越小。
1.3 算法实现
在FPGA 当中,正交坐标系中根据坐标点,可采用查表发或者递归近似法得到角度值。查表法鉴相精度受信号幅值归一化精度影响,因FPGA 中不能直接除法,归一化精度较低,且存储表格占用资源多,为提高鉴相精度和减小资源开销,不采用查表法。CORDIC 算法[3],通过坐标旋转递归近似,随着旋转迭代次数增加,鉴相精度成几何倍数增加,且旋转过程只需要加法和移位完成实现简单[6]。
从这场论争中我们可以看到,在嘉、万文人对“尊元”理念的修正与完善的过程中,其对元曲的评判标准,明显呈现多样化的格局,教化观念、音乐审美、文辞审美、情节设计等多种因素都参与到评判标准的构成中,而不同曲家对不同因素的重视程度的差别,则导致了面对同样的作品出现了截然不同的价值判定。同时页反映出当时戏曲审美的结构尚在调整,还未在诸多审美要素的排序方面形成一个共识性质的基本趋向。
CORDIC 算法原理如下:
点A(x1, y1)旋转θ 到点B(x2, y2):
在由FPGA 为主要数字器件的接收机中,得到
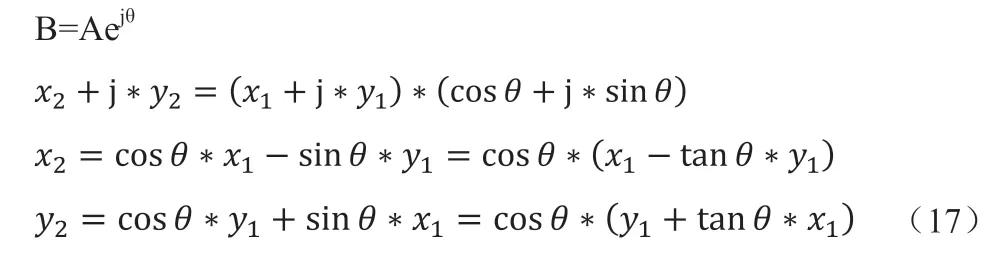
通过多次旋转使得坐标点逼近X 轴,即可完成坐标点的角度θ值计算。
为了FPGA 计算方便,每次旋转取tan θm+1=sign(ym)*2-m,旋转角度θm+1=tan-1[sign(ym)*2-m],cos θ 在不等于零时只影响旋转后的模值,对角度无影响,旋转近似的过程中可忽略。
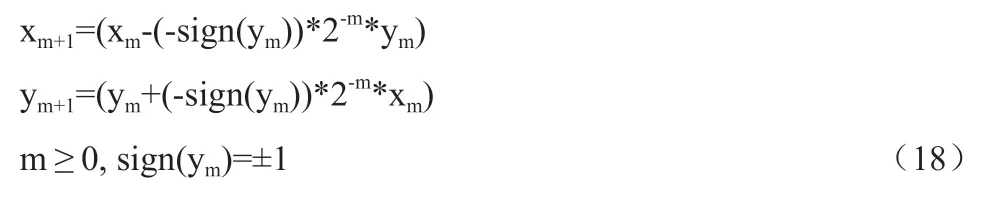
如表2 所示,可以计算出每次旋转迭代的角度。
FPGA 中生成正弦载波可以用NCO 的IP 核,为了方便这里利用fs生成频率为Δ f 的校正载波。
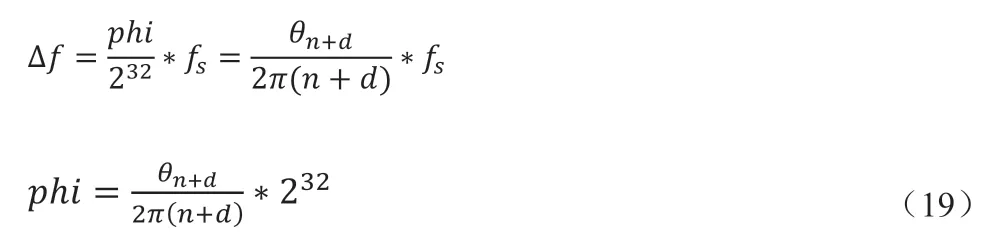
θn+d为角度值时:

迭代次数N 根据精度需求设置:

得到了phi 值,完成了本地校正载波,跟信号y(t)复乘即可完成载波频偏校正。
2 结论
前后相同序列相关求取频偏,对发送序列无特殊要求,可选取帧头或者其他任意已知序列,不增加额外系统开销,在序列长度足够大时,可忽略噪声的影响。用CORDIC 算法递进拟合求频偏的过程中,同步计算NCO 频率字,易于实现并节省运算时间。

